运筹学中excel的运用(用excel解决线性规划、动态规划、排队论等问题)

运筹学数学excel操作实例

两种药品的总利润作为决策目标进入单元格E9，正好位于用来帮助计算总利润的数据单元格的右边.类似于E列的其他输出单元格，E9=C9×C10+D9×D10或E9=SUMPRODUCT（C9：D9，C10：D10）.由于它是在对产量做出决策时目标值定为尽可能大的特殊单元格，所以被称为目标单元格.
根据对上述建模过程的总结，在电子表格中建立线性规划模型的步骤可归纳如下：
回忆例2-1某制药厂的生产计划问题，其求解结果如图13-8所示，即生产4公斤药品Ⅰ和2公斤药品Ⅱ，总利润为1400元.但该最优解是在假设所有的模型参数都准确的前提下做出的，在此基础上，管理层如果进一步考虑下列问题：
图13-11右下部分的“规划求解”对话框显示了求解时应注意的问题：求目标单元格的最大值（利润最大）；约束为设备的实际使用时间小于等于设备的可用时间及实际总业务量小于等于总业务提供量的限制.
打开“选项”对话框，仍选择“采用线性模型”和“假定非负”，回到“规划求解”并按“求解”按钮，得到问题的最优方案为：每月X线及CT检查的业务量分别为1320人次和480人次，磁共振业务量为0，即不必购买该设备；按最优方案安排业务每月可获利55200元.
图13-10的右半部分显示了“规划求解”对话框及“选项”对话框的内容.该问题的目标是所用的胶管原料的总根数最少，因此设置目标单元格为I12等于最小值.由于实际获得的材料数量必须满足需求量的要求，考虑到最优方案（各种截法的某一组合）不一定能使截出的三种材料数量恰好等于需要的数量，而某种材料超过需求量是允许的，故在添加约束时可设置实际截得的数量大于等于需求量，即I9：I12>=K9：K12（本题中，该约束取“>=”和“=”的结果是相同的）；又由于截出的各种材料数量均为整数，因此约束中应包括决策变量取整数的限制，即C13:H13=整数.

EXCEL规划求解功能操作说明

Excel规划求解功能操作说明以Microsoft Excel2003为例，说明使用Excel的求解线性规划问题功能的使用方法。

一、加载规划求解功能1.点击【工具】按钮，在下拉菜单中选择【加载宏】功能。

2.在弹出的【可加载宏】选项卡中勾选【规划求解】，点击确定按钮。

此时，【工具】下拉菜单中增加规划求解功能，表示加载成功。

二、构造表格Excel表格并填入各项数据以教材18页【例题2-8】为例，构造表格如下：1.录入约束条件系数约束条件（1）为5x1+x2-x3+x4=3，则在约束系数的第一行的x1,x2,x3,x4,x5，限制条件，常数b列下分别录入5,1，-1,1,0，=，3如下图所示。

约束系数区的第二行录入约束条件（2）的系数、限制符号及常数b，即-10,6,2,0,1，=，2；约束系数区的第三行录入约束条件（3）（x1≥0）的系数、限制符号及常数b，即1,0,0,0,0，≥，0；约束系数区的第四行录入约束条件（4）（x2≥0）的系数、限制符号及常数b，即0,1,0,0,0，≥，0；约束系数区的第五行录入约束条件（5）（x3≥0）的系数、限制符号及常数b，即0,0,1,0,0，≥，0；约束系数区的第六行录入约束条件（6）（x4≥0）的系数、限制符号及常数b，即0,0,0,1,0，≥，0；约束系数区的第七行录入约束条件（7）（x5≥0）的系数、限制符号及常数b，即0,0,0,0,1，≥，0。

如下图所示。

2.录入目标函数系数目标函数为maxZ=4x1-2x2-x3，则在目标函数的x1,x2,x3,x4,x5列下分别录入4，-2，-1,0,0，如下图所示。

3. 录入约束条件的计算公式双击约束条件（1）行的“总和”单元格，录入以下内容：“=B3*B12+C3*C12+D3*D12+E3*E12+F3*F12”说明：录入的内容即是约束条件（1）的计算公式，其中“B3*B12”代表5x 1; “C3*C12”代表1x 2；“D3*D12”代表-1x 3；“E3*E12”代表1x 4；“F3*F12”代表0x 5。

用Excel求解运筹学问题

Unit Profit Optimal Units Produced for Doors $100 $200 $300 $400 $500 $600 $700 $800 $900 $1,000 Doors 4 2 2 2 2 2 2 2 4 4 4 Windows 3 6 6 6 6 6 6 6 3 3 3 Total Profit $5,500 $3,200 $3,400 $3,600 $3,800 $4,000 $4,200 $4,400 $4,700 $5,100 $5,500
可变单元格单元格名字 $C$12 Units Produced Doors $D$12 Units Produced Windows 约束单元格名字 $E$7 Plant 1 Used $E$8 Plant 2 Used $E$9 Plant 3 Used 终阴影约束允许的允许的值价格限制值增量减量 2 0 4 1E+30 2 12 150 12 6 6 18 100 18 6 6 终递减目标式允许的允许的值成本系数增量减量 2 0 300 450 300 6 0 500 1E+30 300
C D Optimal Units Produced 16 17 Doors Windows 18 =DoorsProduced =WindowsProduced
E Total Prof it =TotalProf it
(1) 只有一个目标函数系数变动的影响
门的单位利润从$100变到$1000，产品组合的变化
５．Under the Tools menu, choose the "Add-Ins" command.
６．Click the Solver Table checkbox to have Solver Table load with Excel every time it is loaded.

Excel求解运筹学问题简介.

Excel求解运筹学问题方法简介Excel中的规划求解是功能强大的优化和资源配置工具。

它可以帮助人们求解运筹学中的许多问题，特别是“规划求解”模块可以解决许多求极值、解方程的问题。

本附件除介绍“规划求解”模块的使用外，还提供给读者“排队论”与“存储论”基本模块。

1 规划求解在使用“规划求解”时，首先需要“规划求解”出现在“工具”菜单中，如果没有，则需要加载“规划求解”宏。

另外，目标函数和约束函数必须要给出公式，变量的约束必须作为约束条件给出。

规划求解的特点：◆表格输入数据不能为分数，当遇到分数时，必须化为小数输入。

◆目标单元格依赖一组单元格（可变单元格），或通过公式间接依赖于可变单元格，规划求解可调整这组单元格来影响目标单元格。

◆目标单元格服从一定的约束和限制。

约束条件不同，结果就不同。

◆可求解特定单元格的最大值或最小值或某个值。

◆对一个问题可以求出多个解。

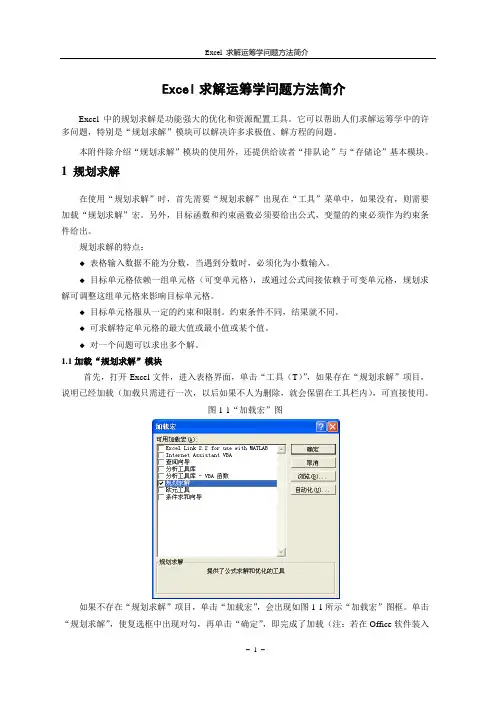
1.1加载“规划求解”模块首先，打开Excel文件，进入表格界面，单击“工具（T）”，如果存在“规划求解”项目，说明已经加载（加载只需进行一次，以后如果不人为删除，就会保留在工具栏内），可直接使用。

图1-1“加载宏”图如果不存在“规划求解”项目，单击“加载宏”，会出现如图1-1所示“加载宏”图框。

单击“规划求解”，使复选框中出现对勾，再单击“确定”，即完成了加载（注：若在Office软件装入时，系统未选择该工具模块装入，此时会引导读者插入软件安装盘，依据系统提示操作即可）。

1.2 线性规划问题求解为了便于说明，以一个线性规划例题来说明这个过程。

例1-1 某工厂在计划期内要安排甲、乙两种产品的生产，已知生产单位产品所需成本分别为2千元和3千元；根据产品特性，产品总数不得少于350件，产品甲不得少于125件；又知生产这两种产品需要某种钢材，产品甲、乙每件分别需要钢材2t 、1t ，钢材的供应量限制在600t 。

问题：工厂应分别生产多少单位甲、乙产品才能使总成本最低？解：容易建立如下线性规划模型。

EXCEL求解线性规划问题

约束右端值降低15时，目旳函数值旳变化量。
解：（1）最优解为x1=0, x2=12.4, x3=9.5
（2） x1旳目旳系数降低5，占允许降低旳百分比=5/∞=0%，x2 旳目旳系数增长4,占允许增长旳百分比=4/7.8=51.2%。
变化旳百分比和为51.2%，没有超出100%，所以最优解不变。
（3）第一资源约束右端值增长30，占允许增长旳30 /∞=0%，第二资源约束右端值增长4 ，占允许增长旳4/15=26.7%，
•初值和终值分别指单元格在此次求解前旳数值和求解后旳数值。
敏感性分析报告（1）
可变单元格中 • “单元格”指决策变量所在单元格旳地址 • “名字”是决策变量旳名称 • “终值”是决策变量旳终值,即最优值 • “递减成本”指最优解中档于0旳变量，相应旳目旳函数中旳系数
增长或降低多少，最优解不再为0 • “目旳式系数”目旳函数中旳系数，为已知条件 • “允许旳增量”与“允许旳减量”表达目旳函数中旳系数在增量
（1）引用旳类型
三种类型：
相对引用、绝对引用、混合引用
（2）相对引用
格式： A3 、B6
使用相对引用后，系统将会记住建立公式旳单元格和被引用旳单元格旳相对位置，在复制这个公式时，新旳公式单元和被引用旳单元依然保持这种相对位置。
（3）绝对引用格式：$a$3 $d$5
绝对引用是指被引用旳单元与引用旳公式单元旳位置关系是绝正确，不论将这个公式复制到任何单元，公式所引用旳还是原来单元格旳数据。
2) 在弹出旳对话框中旳“可用加载宏”列表框中,选定待添加旳加载宏“规划求解”选项旁旳复选框,然后单击“拟定”.单击“拟定” 后,“工具”菜单下就会出现一项“规划求解”
3. “规划求解”各参数设置

EXCEL在运筹学规划论教学中的应用

EXCEL在运筹学规划论教学中的应用作者：于瑛英来源：《教育教学论坛》2014年第10期摘要：运筹学作为一门应用学科，其实验教学逐渐引起重视。

近年来，在教学中使用软件求解运筹学问题已经成为趋势。

鉴于EXCEL应用的广泛性，该文介绍使用EXCEL软件求解运筹学中规划论模型的方法，并详细给出了如何使用EXCEL软件求解线性规划、整数规划、目标规划和动态规划模型。

关键词：运筹学；规划论；EXCEL软件中图分类号G642.4 文献标志码：A 文章编号：1674-9324（2014）10-0278-03一、引言运筹学是一门应用科学，可以为决策者选择最优决策提供定量依据。

运筹学经过多年的发展已经成为体系，包括规划论（线性规划、整数规划、目标规划、动态规划和非线性规划）、图论与网络、排队论、存储论、对策论和决策论等[1]。

传统的运筹学主要是以讲授理论为主，尤其是比较枯燥的数学理论。

近年来，运筹学改革不断提高其应用性，减少枯燥的理论。

此外，随着运筹学计算机支撑技术的迅速发展，运筹学应用得到极大的推动，运筹学实验教学提上日程，因此开设运筹学的实验课程势在必行。

秦必瑜[2]和石磊[3]在运筹学的课程改革中都提出要增加软件应用。

我院运筹学教学团队多年致力于运筹学的教改研究，在提出应用软件的基础上，进一步开设了除理论课程外的专门实践课程，将理论课上学习到的内容使用软件来进行求解。

国内运筹学的实验教学已经有很大进展，目前运筹学经常使用的软件主要有lingo[4][5]、WinQSB[6]、MATLAB[7]等。

近年来，美国高校运筹学（管理科学）的思想、内容、方法和手段发生根本转变，开始使用“电子表格”这一全新的教学方法。

在运筹学中使用EXCEL已经成为运筹学教学的一个新潮流。

EXCEL软件使用方便，不需要重新安装和学习新软件的使用方法，一般的PC机上都安装有EXCEL软件，因此使用方便、应用广泛。

但是目前将EXCEL 在运筹学中的应用并不多，李雪虎[8]给出用EXCEL求解运输问题和网络最优化问题的例子；魏杰羽[9]阐述了用EXCEl求解运输问题的过程；而张辉[10]给出了使用EXCEL求解线性规划问题的例子。

EXCEL在运筹学规划论教学中的应用

采用ＥＸＣＥｂＪ￣解该问题包括以下步骤：第一步：模型输入１．在ＥＸＣＥＬ表格中输入数据，输入目标函数的系数和约束条件的系数２．标识数据，可以用不同颜色标识不同类型的数据３．计算中间数据，数据、公式分离，显示出完整模型第二步：模型求解１．安装 “ 规划求解” 工具。在“ 工具” 中选择“ 加载宏” ，选
关键词：运筹学；规划－￣；ＥＸＣＥＬｌｅｄ，．件
中图分类号Ｇ６４２．４
一
文献标志码：Ａ‘
文章编号：１６７４ — ９３２４（２０１４）１０ — ０２７８ — ０３
、
引言
运筹学是一门应用科学，可以为决策者选择最优决策提供定量依据。运筹学经过多年的发展已经成为体系，包括规划论（线性规划、整数规划、目标规划、动态规划和非线性规划）、图论与网络、排队论、存储论、对策论和决策论等【】１。
论的内容中。运筹学规划论包括线性规划、整数规划、目标
（一）使用ＥＸＣＥＬＳ￣解线性规划模型
Ｍａｘｚ＝２ｘＨ＋３ｘ１２
对于如下线性规划问题，模型１
１＋２ｘ２８４ｘ１ ≤ １６４ｘ， ≤ １６ｘ１，ｘ２＞０￣
传统的运筹学主要是以讲授理论为主，尤其是比较枯燥的数学理论。近年来，运筹学改革不断提高其应用性，减少枯燥的理论。此外，随着运筹学计算机支撑技术的迅速发展，运筹学应用得到极大的推动，运筹学实验教学提上日程，因此开设运筹学的实验课程势在必行。秦必瑜［２１和石磊【在运筹学的课程改革中都提出要增加软件应用。我院运筹学教学团队多年致力于运筹学的教改研究，在提出应用软件的基础上，进一步开设了除理论课程外的专门实践课程，将理论课上学习到的内容使用软件来进行求解。国内运筹学的实验教学已经有很大进展，目前运筹学经常使用的软件主要有ｌｉｎｇｏ［４１５］、ＷｉｎＱＳＢｔ￣、ＭＡＴＬＡＢｍ等。近年来，美国高校运筹学（管理科学）的思想、内容、方法和手段发生根本转变，开始使用“ 电子表格” 这一全新的教学方法。在运筹学中使用ＥＸＣＥＬ已经成为运筹学教学的一个新潮流。ＥＸＣＥＬ软件使用方便，不需要重新安装和学习新软件的使用方法，一般的ＰＣ机上都安装有ＥＸＣＥＬ软件，因此使用方便、应用广泛。但是目前将ＥＸＣＥＬ在运筹学中的应用并不多，李雪虎阎给出用ＥＸＣＥＬ求解运输问题和网络最优化问题的例子；魏杰羽啡目述了用ＥＸＣＥｌ求解运输问题的过程；而张辉［０１给出了使用ＥＸＣＥＬ求解线性规划问题的例子。在运筹学的体系中，内容远远不止这些，即使规划论的内容也不止这些。本文中探讨将ＥＸＣＥＬ￣用于运筹学规划

Excel在求解线性规划问题中的应用

所有的检验数都小于等于０故该表对应的基可行解（妻，Ｏ是，１０），，Ｔ
最优解。３“ ．规划求解” 加载宏方法求解线性规划问题的另一种方法是 “ 规划求解” 加载宏的方法，该方法简单、方便、捷，大提高了计算的效率和准确性，直接得到最快大能
单纯形法［图解法仅仅适用于含有两个决策变量的规划问题，ＪＪ，而单纯形法适用于含有三个及其三个以上决策变量的线性规划问题，应用范围更广，但应用单纯形法时，涉及的计算量大。为了减少计算量，本文一方面借助Ｅｃｌｘｅ软件的表格和计算功能，现了单纯形法；一方面应实另用“ 规划求解” 加载宏的方法直接求解线性规划问题，得到最优解。
１引言．
线性规划问题属于运筹学的一个分支，在经济学、理学以及生它管产生活中有着广泛的应用。求解线性规划问题的方法主要有图解法和
为１所在列的其他元素变为Ｏ，５，得到的新矩阵再反映在新单纯形表中，根据检验数计算公式应用ｓｍｒｄｃ函数计算检验数，并ｕｐｏｕｔ得到的新单纯形表如表２所示。
ｌ墓Ｉｂ０ｆ翱Ｉ９０ｌｌ８
Ｏｊ
Ｘｌ３
１Ｏ
Ｘ２４２
５
Ｘ３１Ｏ
０
Ｘｔ０ｌ
Ｏ
在这个初始单纯形表中，据单纯形法，ＥｃｌＤ根在ｘｅ的５单元格中输人计算公式 “ Ｄ — ｕＰ０ｕＴ￥￥：￥，３４” ＝ＩｓＭＲＤｃ（Ａ３Ａ４：），￥ＤＤ可得决策变量Ｘ，的检验数，复制Ｄ５单元格，别粘贴在Ｅ，５Ｇ分５Ｆ，５单元格，到决策得变量ｘ＇Ｘ的检验数。该表对应一个基可行解（，，，由于存在检验２４ｘＯ０８，９）

精编Excel求解运筹学问题资料

450
300
6
0
500 1E+30
300
终阴影约束允许的允许的
值价格限制值增量减量
20
4 1E+30
2
12 150
12
6
6
18 100
18
6
6
极限值报告
Microsoft Excel 9.0 极限值报告工作表 [Book1]Sheet1 报告的建立: 2006-7-18 10:04:47
1
0
0
2
3
2
Doors 1
Windows 1
Hours Used
1 2 5
Hours
Available
<=
1
<=
12
<=
18
Total Profit $800
第六步: 完成求解对话框第七步:求解方式的选择
第八步: 从求解结果对话框选择所要的报告
Wyndor Glass Co. Product-Mix Problem
1 2 5
Hours
Available
<=
4
<=
12
<=
18
Total Profit $800
第五步: 增加约束条件
Unit Profit
Plant 1 Plant 2 Plant 3
Units Produced
Doors $300
Windows $500
Hours Used Per Unit Produced
第四步: 激活规划求解, 确定可变单元格和目标单元格
Unit Profit
Plant 1 Plant 2 Plant 3

用Excel求解LP(线性规划)问题

③光标指向“约束”栏，按“添加”，光标指向“约束” 添加” 出现“添加约束”对话框（如下图），出现“添加约束”对话框（如下图），
对话框“改变约束”
依次填入约束关系，每输完一条，按“添加”，输入所有约束条件后，按“确定”，
又退回到下图状态，在下图中可以选又退回到下图状态，更改” 删除” 全部重设” “更改”、“删除”、“全部重设” 来编辑约束条件及其他设置。来编辑约束条件及其他设置。
结果
最后得到LP问题的求最后得到LP问题的求解结果(如下图8)，最解结果(如下图8)，最优解X1=2.909(即优解X1=2.909(即 32/11),X2=2.727(即 32/11),X2=2.727(即 30/11), 目标函数的最优值为28。优值为28。
求解的结果
填入了参数的对话框“规划求解参数”
④在上图中按“求解”，即进入求解过程，求在上图中按“求解” 即进入求解过程，解结束，出现“规划求解结果”对话框( 解结束，出现“规划求解结果”对话框(如下选择“保存规划求解结果” 图)，选择“保存规划求解结果”后，
对话框“规划求解结果”
工作表中可变单元格、目标单元格以及计算约束条件的单元格均发生变化。如不想破坏原始数据，可选择“恢复为原值”，同时选中“报告”框中的“运算结果报告”，或选“保存方案”以存储运算结果。
图1. 加载宏
以下面的LP为例，以下面的LP为例，看如何利用 LPin f = 4x1+6x2 s.t. 3x1 - x2 ≥ 6 x1 + 2x2 ≤ 10 7x1 - 6x2 ＝ 4 x1 , x2 ≥ 0
2、输入系数：输入系数：
在单元格A2:D4中分在单元格A2:D4中分别输入两个不等式约束的系数与常数项, 束的系数与常数项,在单元格A5:B5中分别单元格A5:B5中分别输入目标函数的两个系数,在单元格A1:B1 系数,在单元格A1:B1 中任意输入两个数分别作为决策变量x1,x2 别作为决策变量x1,x2 的值(如右图，C 的值(如右图，C列暂空) 。

用excel进行线性规划求解

步骤1 单击[工具]菜单中的[规划求解]命令。

步骤2 弹出[规划求解参数]对话框，在其中输入参数。

置目标单元格文本框中输入目标单元格；[等于]框架中选中[最大值＼最小值〕单选按钮。

步骤3 设置可变单元格区域，按Ctrl键，用鼠标进行选取，或在每选一个连续区域后，在其后输入逗号“，”。

步骤4 单击[约束〕框架中的[添加]按钮。

步骤5 在弹出的[添加约束]对话框个输入约束条件．
步骤6 单击[添加]按钮、完成一个约束条件的添加。

重复第5步，直到添加完所有条件
步骤7 单击[确定]按钮，返回到[规划求解参数]对话框，完成条件输入的[规划求解参数]对话框。

步骤8 点击“求解器参数”窗口右边的“选项”按钮。

确信选择了“采用线性模型”旁边的选择框。

这是最重要的一步工作！如果“假设为线性模型”旁边的选择框没有被选择，那么请选择，并点击“确定”。

如果变量全部非负，而“假定变量非负”旁边的选择框没有被选择，那么请选择，并点击“确定”。

步骤9 单击[求解]按钮，弹出[规划求解结果]对话柜，同时求解结果显示在工作表中。

步骤10 若结果满足要求，单击[确定]按钮，完成操作；若结果不符要求，单击[取消]按钮，在工作表中修改单元格初值后重新运行规划求解过程。

运用EXCEL求解线性规划模型

EXCEL求解线性规划模型
线性规划问题解的讨论线性规划问题解的种类？唯一解的表现是……？无穷解的表现是……？无可行域无解的表现是……？可行域无界的表现是……？上述结果用EXCEL建模求解的最后对话框提示不同。
01
图解法解得分析：
02
解的结果
03
有可行域
04
无可行域
05
可行域有界
06
可行域无界
▍单击“粘贴列表”，在电子表格中的相应位置得出结果。
将单元格名称粘贴到电子表格中
EXCEL求解线性规划模型
EXCEL求解线性规划模型
EXCEL求解线性规划模型
对结果进行修饰利用“替换”功能中的“全部替换”去掉“=Sheet1!”和“$”，得出区域名称和引用结果。
EXCEL求解线性规划模型
规划求解过程
删除：选择欲删除单元格名称，单击“删除”。
3
1
2
4
路径：“插入”——“名称”——“定义”，进入“定义名称” 界面。
单击某个名称，可查看其引用位置。
更改：先添加新名称，再删除原名称。也可修改原名称的引用位置。
查看、更改、删除
EXCEL求解线性规划模型
查看、更改、删除操作界面
EXCEL求解线性规划模型
07
唯一解
08
无穷解
09
唯一解
10
无穷解
11
无解
12
一定无解
EXCEL求解线性规划模型
线性规划问题的灵敏度分析是在求出最优解的基础上，进一步讨论当cj、bi、aij发生变化时，对最优解的影响。
判断某一参数发生变化，原最优解是否发生变化？
02
怎样得出使原最优解不变的参数变化范围

使用Excel进行线性规划求解功能，轻松找到问题的最优的解决方案

使用Excel进行线性规划求解功能，轻松找到问题的最优的解
决方案
在我们的工作中，规划求解是十分常见的应用场景，是一种研究线性约束条件下线性目标函数的极值问题的数学理论和方法。

比如在生产管理中，在人工、材料等等条件的约束下，如何安排才能使工厂利益的最大化问题就是典型的规划问题。

而对于此类问题的求解，如果使用手工求解的方式还是存在一定的困难，但是如果使用Excel这个工具的话，就能轻松的进行求解。

下面，我就通过一个工厂生产利润最大化的例子来给小伙伴们讲解下具体的使用方法。

题目：某家具生产厂可以生产A、B、C、D四种家具，四种家具所需要的人工、木材、玻璃等的量是不同的，同时由于市场
的限制，每种家具的最大销售量也是有限制的。

四种家具的所
需材料、市场限额、利润见下表：
根据上述要求，可以设该厂生产A、B、C、D四种家具的量分别为X1、X2、X3、X4，则利润为：maxZ=60X1+66X2+40X3+50X4。

约束条件如下：
根据以上条件，在Excel中做出以下求解模版：
根据以上分析，目标值单元格的公式如下：
=SUMPRODUCT(B13:E13,B6:E6)。

时间约束，木材约束，玻璃约束的使用量公式分别为：=SUMPRODUCT(B18:E18,$B$13:$E$13)
=SUMPRODUCT(B19:E19,$B$13:$E$13)
=SUMPRODUCT(B20:E20,$B$13:$E$13)
专栏
从进销存系统入门ExcelVBA编程。

运筹学实验3用Excel求解线性规划模型

实验三、用Excel求解线性规划模型线性规划问题用手工求解工作量很大，而且没有较高的数学基础很难理解其计算过程和方法，但是借助Excel“规划求解”工具，就能轻而易举地求得结果。

Excel最多可解200个变量、600个约束条件的问题。

下面我们以一实例介绍利用Excel规划求解工具怎样快速解决具体的经济决策问题。

一、实验目的1、掌握如何建立线性规划模型。

2、掌握用Excel求解线性规划模型的方法。

3、掌握如何借助于Excel对线性规划模型进行灵敏度分析，以判断各种可能的变化对最优方案产生的影响。

4、读懂Excel求解线性规划问题输出的运算结果报告和敏感性报告。

二、实验内容1、[工具][规划求解]命令规划求解加载宏是Excel的一个可选安装模块，在安装Excel时，只有在选择“完全/定制安装”时才可选择装入这个模块。

在安装完成进入Excel后还要用[工具][加载宏]命令选中“规划求解”，以后在[工具]菜单下就增加了一条[规划求解]命令。

使用[规划求解]命令的一般步骤为：第一步：在选取[工具][规划求解]命令后，弹出图1所示“规划求解参数”对话框，其中各选项说明如表1。

图1“规划求解参数”对话框选项名说明设置目标单元格选取计算问题的目标函数，并含有计算公式的单元格等于按问题目标进行选择。

如利润问题，选取“最大值”可变单元格决策变量所在各单元格、不含公式，可以有多个区域或单元格约束增加、修改、删除各个约束等式或不等式，一个一个地与图2切换填入或修改添加选择后弹出图2所示对话框更改选择后弹出图3所示对话框删除删除所选定的约束条件选项决定采用线性模型还是非线性模型求解约束条件中的单元格引用位置，可从键盘直接录入，也可用鼠标拖放选取。

图2图3第二步：完成图1所示的一切填入项目后，单击“选项”按钮，在弹出的“规划求解选项”对话框中若是线性模型则选取“采用线性规模”选项按钮，再单击“确定”按钮回到图1。

图4第三步：在图1中单击“求解”按钮，经计算完成后弹出“规划求解结果”对话框（图5）。

利用excel软件求解线性规划问题讲解

下面我们通过一个例子来解释怎样用“规划求解”来求解数学规划问题。

例1 公司通常需要确定每月（或每周）生产计划，列出每种产品必须生产的数量。

具体来说就是，产品组合问题就是要确定公司每月应该生产的每种产品的数量以使利润最大化。

产品组合通常必须满足以下约束：● 产品组合使用的资源不能超标。

● 对每种产品的需求都是有限的。

我们每月生产的产品不能超过需求的数量，因为生产过剩就是浪费（例如，易变质的药品）。

下面，我们来考虑让某医药公司的最优产品组合问题。

该公司有六种可以生产的药品，相关数据如下表所示。

设该公司生产药品1～6的产量分别为126,,,x x x （磅），则最优产品组合的线性规划模型为123456123456123456123456max 6 5.3 5.4 4.2 3.8 1.86543 2.5 1.545003.2 2.6 1.50.80.70.316009609281041..977108410550,16j z x x x x x x x x x x x x x x x x x x x x x s t x x x x j =++++++++++≤⎧⎪+++++≤⎪⎪≤⎪≤⎪⎪≤⎨⎪≤⎪≤⎪⎪≤⎪⎪≥≤≤⎩下面用规划求解加载宏来求解这个问题：首先，如下如所示，在Excel 工作表内输入目标函数的系数、约束方程的系数、右端常数项；其次，选定目标函数单元、可变单元、约束函数单元，定义目标函数、约束函数其中，劳动力约束函数的定义公式是“=MMULT(B3:G3, J5:J10)”，原料约束函数的定义公式是“＝MMULT(B4:G4,J5:J10)”，目标函数的定义公式是“MMULT(B5:G5, J5:J10)”。

注：函数MMULT(B3:G3, J5:J10)的意义是：单元区B3:G3表示的行向量与单元区J5:J10表示的列向量的内积。

这一要特别注意的是，第一格单元区必须是行，第二格单元区必须是列，并且两个单元区所含的单元格个数必须相等。

excel在运筹学中的应用1

3 开通
5. 洛→旧 2
3
55
开通
6. 芝→丹
33
4
开通
7. 芝→西
33
3 3 4 开通
8. 丹→旧
2
44
5
开通
9. 丹→芝
2
2
2
开通
10. 西→旧
2
44
5 开通
11. 西→洛
2
2 4 4 2 开通
成本(千元) 2 3 4 6 7 5 7 8 9 9 8 9
16
设 12 个 0-1 变量 x j = 1（取第 j 航程），0（不取第 j 航程）
≤5
值11x1 + 15x2 + 25x3 + 20x4 + 10x5 + 12x6 + 3x7 ≥ 13
•
现金x存1 +
3x2 15x2
+ +
8x3 30x3
+ +
6x4 20x4
+ +
x5 15x5
+ +
2x6 10x6
≤4 ≥ 10
款 x1 + x2 + x3 + x4 + x5 + x6 + x7 = 1
总利润 Z
s.t.
单件消耗量资源 1 资源 2 资源 3
产品Ⅰ
2 1 4
产品Ⅱ
2 2 0
可利用
12 8 16
Z = 2x1 + 3x2
2x1 +2x2 ≤ 12
x1 +2x2 ≤ 8
4x1
≤ 16
4x2 ≤ 12 x1, x2 ≥ 0

运筹学利用Excel课程设计

运筹学利用Excel课程设计一、课程目标知识目标：1. 让学生掌握运筹学基本概念，理解线性规划、整数规划等基本模型；2. 培养学生运用Excel进行数据处理和分析的能力，掌握运用Excel求解线性规划问题的方法；3. 使学生了解运筹学在实际生活中的应用，如资源配置、生产计划等。

技能目标：1. 培养学生运用Excel进行运筹学模型建立、求解和结果分析的能力；2. 培养学生运用运筹学知识解决实际问题的能力，提高解决问题的效率和准确性；3. 提高学生的团队协作能力和沟通能力。

情感态度价值观目标：1. 培养学生对运筹学学科的兴趣，激发学生主动学习的热情；2. 培养学生严谨、认真的学习态度，养成科学研究和解决问题的良好习惯；3. 培养学生关注社会现象，运用所学知识为社会发展和进步贡献力量的意识。

课程性质：本课程属于应用性较强的学科，旨在培养学生运用运筹学知识解决实际问题的能力。

学生特点：学生具备一定的数学基础和计算机操作能力，对实际问题具有较强的探究欲望。

教学要求：结合学生特点，注重理论与实践相结合，提高学生的实际操作能力和解决问题的能力。

在教学过程中，注重引导学生主动参与，培养学生的团队协作能力和沟通能力。

通过课程学习，使学生能够将所学知识应用于实际生活和工作中。

二、教学内容1. 运筹学基本概念：讲解线性规划、整数规划等基本模型，以及相关定义和性质。

教材章节：第一章运筹学基本概念内容安排：2课时2. Excel基础操作：介绍Excel的基本功能，包括数据录入、公式运用、图表制作等。

教材章节：第二章 Excel基础操作内容安排：2课时3. 线性规划模型建立与求解：讲解如何利用Excel建立线性规划模型，并进行求解。

教材章节：第三章线性规划内容安排：4课时4. 整数规划模型建立与求解：介绍整数规划的特点，以及如何利用Excel求解整数规划问题。

教材章节：第四章整数规划内容安排：4课时5. 运筹学在实际生活中的应用：分析资源配置、生产计划等实际问题，并运用Excel进行求解。

运筹学中excel的运用(用excel解决线性规划、动态规划、排队论等问题)

合集下载

运筹学数学excel操作实例

EXCEL规划求解功能操作说明

用Excel求解运筹学问题

Excel求解运筹学问题简介.

EXCEL求解线性规划问题

EXCEL在运筹学规划论教学中的应用

EXCEL在运筹学规划论教学中的应用

Excel在求解线性规划问题中的应用

精编Excel求解运筹学问题资料

用Excel求解LP(线性规划)问题

用excel进行线性规划求解

运用EXCEL求解线性规划模型

使用Excel进行线性规划求解功能，轻松找到问题的最优的解决方案

运筹学实验3用Excel求解线性规划模型

利用excel软件求解线性规划问题讲解

excel在运筹学中的应用1

运筹学利用Excel课程设计

文档推荐

最新文档