证券投资中的数学

高中数学研究性学习课题集锦篇一：高中数学研究性学习课题题目精选高中数学|研究性学习|课题|题目精选精选高中数学研究性学习课题题目精选. 1、银行存款利息和利税的调查. 2、气象学中的数学应用问题. 3、如何开发解题智慧. 4、多面体欧拉定理的发现.5、购房贷款决策问题 ...骑大象的蚂蚁整理编辑高中数学|研究性学习|课题|题目精选高中数学研究性学习课题题目精选1、银行存款利息和利税的调查2、气象学中的数学应用问题3、如何开发解题智慧4、多面体欧拉定理的发现5、购房贷款决策问题6、有关房子粉刷的预算7、日常生活中的悖论问题8、关于数学知识在物理上的应用探索9、投资人寿保险和投资银行的分析比较10、黄金数的广泛应用11、编程中的优化算法问题12、余弦定理在日常生活中的应用13、证券投资中的数学14、环境规划与数学15、如何计算一份试卷的难度与区分度16、数学的发展历史17、以“养老金”问题谈起18、中国体育彩票中的数学问题19、“开放型题”及其思维对策20、解答应用题的思维方法21、高中数学的学习活动——解题分析 A）从尝试到严谨、B）从一个到一类22、高中数学的学习活动——解题后的反思——开发解题智慧23、中国电脑福利彩票中的数学问题24、各镇中学生生活情况25、城镇/农村饮食构成及优化设计26、如何安置军事侦察卫星27、给人与人的关系（友情）评分28、丈量成功大厦29、寻找人的情绪变化规律30、如何存款最合算31、哪家超市最便宜32、数学中的黄金分割33、通讯网络收费调查统计34、数学中的最优化问题35、水库的来水量如何计算36、计算器对运算能力影响37、数学灵感的培养38、如何提高数学课堂效率39、二次函数图象特点应用40、D中线段计算41、统计溪美月降水量42、如何合理抽税43、南安市区车辆构成44、出租车车费的合理定价45、衣服的价格、质地、品牌，左右消费者观念多少？46、购房贷款决策问题篇二：高中数学研究性学习课题选题参考高中数学研究性学习课题选题参考数学研究性学习课题1、银行存款利息和利税的调查2、气象学中的数学应用问题3、如何开发解题智慧4、多面体欧拉定理的发现5、购房贷款决策问题6、有关房子粉刷的预算7、日常生活中的悖论问题8、关于数学知识在物理上的应用探索9、投资人寿保险和投资银行的分析比较10、黄金数的广泛应用11、编程中的优化算法问题12、余弦定理在日常生活中的应用13、证券投资中的数学14、环境规划与数学15、如何计算一份试卷的难度与区分度16、数学的发展历史17、以“养老金”问题谈起18、中国体育彩票中的数学问题19、“开放型题”及其思维对策20、解答应用题的思维方法21、高中数学的学习活动——解题分析 A）从尝试到严谨、B）从一个到一类22、高中数学的学习活动——解题后的反思——开发解题智慧23、中国电脑福利彩票中的数学问题24、各镇中学生生活情况25、城镇/农村饮食构成及优化设计26、如何安置军事侦察卫星27、给人与人的关系（友情）评分28、丈量成功大厦29、寻找人的情绪变化规律30、如何存款最合算31、哪家超市最便宜32、数学中的黄金分割33、通讯网络收费调查统计34、数学中的最优化问题35、水库的来水量如何计算36、计算器对运算能力影响37、数学灵感的培养38、如何提高数学课堂效率39、二次函数图象特点应用40、统计月降水量41、如何合理抽税42、市区车辆构成43、出租车车费的合理定价44、衣服的价格、质地、品牌，左右消费者观念多少？45、购房贷款决策问题研究性学习的问题与课题《立几部分》问题1平几中证点共线、线共点往往较难，通常出现在竞赛中。

股票投资中概率论和数理统计的运用文/秦秉杰摘要：收益与风险并存是股票投资的重要特征，风险控制的质量会对股票投资的效益产生至关重要的影响。

以最低的风险获得最大的投资效益是股票投资者的目标，但是实际上股票投资者必须要面对股票下跌、投资不当等情况发生所带来的巨大风险，且股票投资的风险是无法完全消除的，只能尽可能规避，通过概率论与数理统计相关知识的运用可以为对股票投资进行科学的分析，为股票投资提供依据提高风险控制的成效。

本文就股票投资中概率论和数理统计的具体运用进行了分析和探讨。

关键词：股票投资；概率论；数理统计；运用股票作为一项高风险高回报的投资活动，伴随着市场经济的日渐成熟股票投资者的数量也日渐增多。

股票投资的风险性是无法避免的，股票市场中事件的发生存在随机性，利用概率论和数理统计可以对股票市场中的随机现象进行数据的统计和理性的分析，从而为投资者的投资行为提供参考，概率论与数理统计在股票中应用是规避股票投资风险的重要途径。

一、概率论与数理统计的内涵概率论是以大量随机事件的理性分析为基础，进而对特定事件出现的几率进行计算和判断，比较和分析不同情况下事件发生的可能性结果，对可能性之间的关联预测可能出现的问题的理论方法。

概率论通过科学的分析对随机事件的影响因素进行分析，并且对特定状况下可能发生的问题进行推测，进而为决策提供依据，目前概率论在不同的行业领域中得到了广泛的应用，同时也促生了一些其他相关理论的出现。

概率论在风险投资中运用具有巨大的优势，股票市场中的现象大多是随机的，整体来看似乎并没有什么规律，而概率论通过对随机事件的分析可以找出其内在的关联和规律。

概率论应用成效会影响到股票投资者的效益、股票发行者的利益乃至整个股票市场的稳定性。

概率论是数理统计的基础，作为由概率论发展而来的数学理论方法，数理统计主要是对随机因素影响的数据进行收集整理和研究分析，以此为依据对相关事件进行预测，为决策行为提供依据和参考。

高中数学研究性学习课题集锦篇一：高中数学研究性学习课题题目精选高中数学|研究性学习|课题|题目精选精选高中数学研究性学习课题题目精选. 1、银行存款利息和利税的调查. 2、气象学中的数学应用问题. 3、如何开发解题智慧. 4、多面体欧拉定理的发现. 5、购房贷款决策问题...骑大象的蚂蚁整理编辑高中数学|研究性学习|课题|题目精选高中数学研究性学习课题题目精选1、银行存款利息和利税的调查2、气象学中的数学应用问题3、如何开发解题智慧4、多面体欧拉定理的发现5、购房贷款决策问题6、有关房子粉刷的预算7、日常生活中的悖论问题8、关于数学知识在物理上的应用探索9、投资人寿保险和投资银行的分析比较10、黄金数的广泛应用11、编程中的优化算法问题12、余弦定理在日常生活中的应用13、证券投资中的数学14、环境规划与数学15、如何计算一份试卷的难度与区分度16、数学的发展历史17、以“养老金”问题谈起18、中国体育彩票中的数学问题19、“开放型题”及其思维对策20、解答应用题的思维方法21、高中数学的学习活动——解题分析A）从尝试到严谨、B）从一个到一类22、高中数学的学习活动——解题后的反思——开发解题智慧23、中国电脑福利彩票中的数学问题24、各镇中学生生活情况25、城镇/农村饮食构成及优化设计26、如何安置军事侦察卫星27、给人与人的关系（友情）评分28、丈量成功大厦29、寻找人的情绪变化规律30、如何存款最合算31、哪家超市最便宜32、数学中的黄金分割33、通讯网络收费调查统计34、数学中的最优化问题35、水库的来水量如何计算36、计算器对运算能力影响37、数学灵感的培养38、如何提高数学课堂效率39、二次函数图象特点应用40、D中线段计算41、统计溪美月降水量42、如何合理抽税43、南安市区车辆构成44、出租车车费的合理定价45、衣服的价格、质地、品牌，左右消费者观念多少？46、购房贷款决策问题篇二：高中数学研究性学习课题选题参考高中数学研究性学习课题选题参考数学研究性学习课题1、银行存款利息和利税的调查2、气象学中的数学应用问题3、如何开发解题智慧4、多面体欧拉定理的发现5、购房贷款决策问题6、有关房子粉刷的预算7、日常生活中的悖论问题8、关于数学知识在物理上的应用探索9、投资人寿保险和投资银行的分析比较10、黄金数的广泛应用11、编程中的优化算法问题12、余弦定理在日常生活中的应用13、证券投资中的数学14、环境规划与数学15、如何计算一份试卷的难度与区分度16、数学的发展历史17、以“养老金”问题谈起18、中国体育彩票中的数学问题19、“开放型题”及其思维对策20、解答应用题的思维方法21、高中数学的学习活动——解题分析A）从尝试到严谨、B）从一个到一类22、高中数学的学习活动——解题后的反思——开发解题智慧23、中国电脑福利彩票中的数学问题24、各镇中学生生活情况25、城镇/农村饮食构成及优化设计26、如何安置军事侦察卫星27、给人与人的关系（友情）评分28、丈量成功大厦29、寻找人的情绪变化规律30、如何存款最合算31、哪家超市最便宜32、数学中的黄金分割33、通讯网络收费调查统计34、数学中的最优化问题35、水库的来水量如何计算36、计算器对运算能力影响37、数学灵感的培养38、如何提高数学课堂效率39、二次函数图象特点应用40、统计月降水量41、如何合理抽税42、市区车辆构成43、出租车车费的合理定价44、衣服的价格、质地、品牌，左右消费者观念多少？45、购房贷款决策问题研究性学习的问题与课题《立几部分》问题1平几中证点共线、线共点往往较难，通常出现在竞赛中。

第六章资产组合管理主要内容资产组合的定义及理论源起，资产组合的收益与风险评价，资产组合的效率边界，投资组合的风险分散效应，资产组合理论的应用与局限。

重点难点•重点：资产组合的概念，资产组合的收益与风险评价，资产组合的效率边界。

•难点：资产组合的局限。

第一节投资收益和风险问题的引入•投资者制定投资目标应考虑回报和风险–投资者厌恶风险，承担风险需要补偿–不同的投资者对风险厌恶程度不一样，怎样刻画不同投资者对收益-风险之间的权衡关系•回报和风险的度量•例子：下一年你有5000块钱用于投资，投资一年，有六种投资机会供选择：–（1）30天到期、现在年收益率为6%的货币市场基金–（2）一年定期存款，利率为7.5%–（3）10年期长期国债，每年收益为9%–（4）一种股票，现价10元/股，下一年的预期股价为11.2元/股，且估计红利为0.2元–（5）一人向你借钱，期限一年，利率15%–(6）以8.4元人民币兑1美元买外汇•问题–各种投资的收益水平如何–各种投资有哪些风险，如何度量风险–各种投资的风险和收益的组合情况如何–如何进行投资决策（一种或多种组合投资）一、投资收益的度量－利率• 1.按计息的方式分：单利(simple rate)；复利(compound rate)•TV-----total value P-----principal（1）终值（final value, FV）和现值(present value, PV)简式贷款中，贷款人向借款人提供一笔资金（本金，P），借款人于到期日连本带利偿还。

如p＝1000，一年后偿还本金1000及利息I＝100。

一年后的1100等于现在的1000元按一定的利率水平（10％）计算，现在的1000元，一年后的终值为1100元；或者说：一年后的1100元，现值为1000元•终值：计算某项资产P在n期后的价值，称为终值FV（final value）•计算过程中，利息以单利还是复利计呢•－－复利•FV=P·(1+i)n•(期限是n，i为与期限一致的利率水平，按n期计复利)•例如：如果按月计复利，i为月利率1%，则现在的1000元6个月后的终值为•FV=1000×(1+1%)6•现值（PV，present value）:•把未来的R元贴现到现在的价值，就是未来R元的现值，计算公式为•计算未来收入在今天的价值过程，称为对未来的贴现,利率i也称为贴现率(discount ratio)或贴现因子(discount factor)复利(年利率为6％)•复利频率n复利水平(%)•年 1 6.00000•半年 2 6.09000•季 4 6.13636•月12 6.16778•周52 6.17998•日365 6.18313（2）连续复利的计算•在上例中，e 0.06=1.0618365，因此，我们可以说，利息为6%的债券的连续复利为每年6.18365%。

金融数学在证券投资中的应用研究一、介绍金融数学，是指将数学方法应用于金融领域，用数学技术处理金融问题的一门学科，也是现代金融学不可或缺的一部分。

而证券投资，则是常见的金融领域之一。

在证券投资中，金融数学的应用既能提高投资效率，也能降低风险和成本。

二、金融数学在证券投资中的应用2.1 证券的定价模型证券定价是确认证券市场价值的过程。

基本定价方法包括资本资产定价模型（CAPM）和期权定价模型。

其中，CAPM模型是股票和证券市场上最常用的定价模型之一，它通过测量风险和回报之间的关系，解决证券市场的基本问题。

2.2 风险度量及证券投资风险控制在证券投资中，风险度量及风险控制是重要的投资决策因素。

常用的风险度量方法有标准差和Beta系数。

Beta系数是资本市场线的比率，可以表示整个市场的波动率。

因此，它是证券分析家在风险控制中使用的一种判断标准。

2.3 统计学分析及相应的应用统计分析在证券投资中也非常重要。

其中，常用的统计学方法包括线性回归（LR）和非线性回归（NLR）。

这些方法可以帮助股票分析师预测市场未来的走势，以便做好相应的投资决策。

2.4 投资组合理论投资组合理论是一种可以帮助投资者在现有资产中分散风险的数学方法。

它是基于资产的收益率和风险作为分散投资组合的基本方法。

通过投资组合的合理搭配，可以使投资者更有效地利用资产，实现超额回报。

三、结论综上所述，金融数学在证券投资中的应用十分广泛，不仅可以定价证券、度量风险和控制风险，还应用于股票预测和投资组合。

虽然这些方法并不能保证完全避免投资风险和损失，但有效的利用数学工具仍能对投资者取得更优秀的投资回报。

第九章证券投资技术分析主要理论与方法二、名词解释K线、开盘价、收盘价、最高价、最低价、阳线、阴线、影线、跳空、空头、多头、支撑线、压力线、趋势线、轨道线、黄金分割线、百分比线、速度线、甘氏线、反转形态、整理形态、头肩顶、头肩底、双重底、双重顶、三重底、三重顶、圆形底、圆形顶、三角形、矩形、楔形、旗形、喇叭形、菱形、V形、突破、随机漫步理论、循环周期理论、相反理论。

1. K线：Ｋ线图最早是日本德川幕府时代大阪的米商用来记录当时一天、一周或一月中米价涨跌行情的图示法，后被引入股市。

Ｋ线图有直观、立体感强、携带信息量大的特点，蕴涵着丰富的东方哲学思想，能充分显示股价趋势的强弱、买卖双方力量平衡的变化，预测后市走向较准确，是应用较多的技术分析手段。

2. 开盘价：目前我国股票市场采用集合竞价的方式产生开盘价。

3. 收盘价：是多空双方经过一段时间的争斗后最终达到的共识，是供需双方最后的暂时平衡点，具有指明价格的功能。

4. 最高价：是交易过程中出现的最高的价格。

5. 最低价：是交易过程中出现的最低的价格。

6. 阳线：收盘价高于开盘价时用空（或红）实体表示，称为阳线。

7. 阴线：开盘价高于收盘价时用黑（或蓝）实体表示，称为阴线。

8. 影线：影线表示高价和低价。

9.跳空：股价受利多或利空影响后，出现较大幅度上下跳动的现象。

大小所决定．10、空头：空头是投资者和股票商认为现时股价虽然较高，但对股市前景看坏，预计股价将会下跌，于是把借来的股票及时卖出，待股价跌至某一价位时再买进，以获取差额收益。

空头指的是变为股价已上涨到了最高点，很快便会下跌，或当股票已开始下跌时，认为还会继续下跌，趁高价时卖出的投资者。

采用这种先卖出后买进、从中赚取差价的交易方式称为空头。

人们通常把股价长期呈下跌趋势的股票市场称为空头市场，空头市场股价变化的特征是一连串的大跌小涨。

11、多头：多头是指投资者对股市看好，预计股价将会看涨，于是趁低价时买进股票，待股票上涨至某一价位时再卖出，以获取差额收益。

高中数学研究性学习课题题目精选1、银行存款利息和利税的调查2、气象学中的数学应用问题3、如何开发解题智慧4、多面体欧拉定理的发现5、购房贷款决策问题6、有关房子粉刷的预算7、日常生活中的悖论问题8、关于数学知识在物理上的应用探索9、投资人寿保险和投资银行的分析比较10、黄金数的广泛应用11、编程中的优化算法问题12、余弦定理在日常生活中的应用13、证券投资中的数学14、环境规划与数学15、如何计算一份试卷的难度与区分度16、数学的发展历史17、以“养老金”问题谈起18、中国体育彩票中的数学问题19、“开放型题”及其思维对策20、解答应用题的思维方法21、高中数学的学习活动——解题分析A）从尝试到严谨、B）从一个到一类22、高中数学的学习活动——解题后的反思——开发解题智慧23、中国电脑福利彩票中的数学问题24、各镇中学生生活情况25、城镇/农村饮食构成及优化设计26、如何安置军事侦察卫星27、给人与人的关系（友情）评分28、丈量成功大厦29、寻找人的情绪变化规律30、如何存款最合算31、哪家超市最便宜32、数学中的黄金分割33、通讯网络收费调查统计34、数学中的最优化问题35、水库的来水量如何计算36、计算器对运算能力影响37、数学灵感的培养38、如何提高数学课堂效率39、二次函数图象特点应用40、D中线段计算41、统计溪美月降水量42、如何合理抽税43、南安市区车辆构成44、出租车车费的合理定价45、衣服的价格、质地、品牌，左右消费者观念多少？46、购房贷款决策问题（注：文档可能无法思考全面，请浏览后下载，供参考。

可复制、编制，期待你的好评与关注！）。

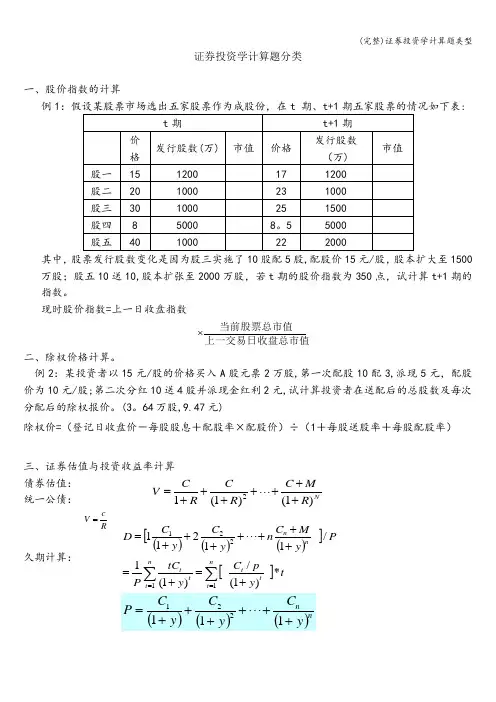
证券投资学计算题分类一、股价指数的计算例1:其中，股票发行股数变化是因为股三实施了10股配5股,配股价15元/股，股本扩大至1500万股；股五10送10,股本扩张至2000万股，若t 期的股价指数为350点，试计算t+1期的指数。

现时股价指数=上一日收盘指数二、除权价格计算。

例2：某投资者以15元/股的价格买入A 股元票2万股,第一次配股10配3,派现5元，配股价为10元/股;第二次分红10送4股并派现金红利2元,试计算投资者在送配后的总股数及每次分配后的除权报价。

(3。

64万股,9.47元)除权价=（登记日收盘价－每股股息＋配股率×配股价）÷（1＋每股送股率＋每股配股率）三、证券估值与投资收益率计算 债券估值： 统一公债：久期计算：上一交易日收盘总市值当前股票总市值⨯)1()1(12NR MC R C R C V +++⋅⋅⋅++++=Rc V =[()()()][]ty p C y tC P Py M C n y C y C D nt tt n t t tnn *)1(/)1(1/1121111221∑∑==+=+=+++++++=股票价值计算：四、资本市场理论1、均值——方差模型单种证券的预期收益率与风险∑-==j j j p r r Var 22)()(μσ两种证券的预期收益率与风险一般意义下的两证券最小风险组合:y D y y D P P ∆-=⎪⎪⎭⎫ ⎝⎛+∆-=∆+⨯='11到期收益率到期收益率变化久期价格变化的百分比∑∞=+=++++++=1332210)1()1()1()1(t tt R D R D R D R D P ,)1()1(1110∑-=++=-g R D R g D P tt ∑∑=∞+=-++++=Tt T t tt t T R D R g D P 111110)1()1()1( )1()1(10∑=+++=nt nnn t t R E M R D P ∑==jj j j p r r E )(μ212222]..)1(2)1([)1(B A AB A A B A A A P BA A A P x x x x x x σσρσσσμμμ-+-+=-+=210RDR D P ∆+=当相关系数=1，0，-1时的最小方差组合。

高中数学研究性学习课题选题参考数学研究性学习课题1、银行存款利息和利税的调查2、气象学中的数学应用问题3、如何开发解题智慧4、多面体欧拉定理的发现5、购房贷款决策问题6、有关房子粉刷的预算7、日常生活中的悖论问题8、关于数学知识在物理上的应用探索9、投资人寿保险和投资银行的分析比较10、黄金数的广泛应用11、编程中的优化算法问题12、余弦定理在日常生活中的应用13、证券投资中的数学14、环境规划与数学15、如何计算一份试卷的难度与区分度16、数学的发展历史17、以“养老金”问题谈起18、中国体育彩票中的数学问题19、“开放型题”及其思维对策20、解答应用题的思维方法21、高中数学的学习活动——解题分析A）从尝试到严谨、B）从一个到一类22、高中数学的学习活动——解题后的反思——开发解题智慧23、中国电脑福利彩票中的数学问题24、各镇中学生生活情况25、城镇/农村饮食构成及优化设计26、如何安置军事侦察卫星27、给人与人的关系（友情）评分28、丈量成功大厦29、寻找人的情绪变化规律30、如何存款最合算31、哪家超市最便宜32、数学中的黄金分割33、通讯网络收费调查统计34、数学中的最优化问题35、水库的来水量如何计算36、计算器对运算能力影响37、数学灵感的培养38、如何提高数学课堂效率39、二次函数图象特点应用40、统计月降水量41、如何合理抽税42、市区车辆构成43、出租车车费的合理定价44、衣服的价格、质地、品牌，左右消费者观念多少？45、购房贷款决策问题研究性学习的问题与课题《立几部分》问题1 平几中证点共线、线共点往往较难，通常出现在竞赛中。

而立几中的这类问题却是非简单，主要的依据仅仅是平面的基本性质：两个平面的公共点共线。

可否将平几问题的这类问题进行升维处理。

即把它转化为立几问世题加以解答。

问题2 用运变化的观点对待数学问题，将会发现问题的实质及问题之间的联系，但对于立几中的这方面还显得不够，可以通过整理、收集这方面的材料加以综合研究。

数学小课题研究题目篇一：高中数学课题研究题目高中数学研究性学习课题题目精选1、银行存款利息和利税的调查2、气象学中的数学应用问题3、如何开发解题智慧4、多面体欧拉定理的发现5、购房贷款决策问题6、有关房子粉刷的预算7、日常生活中的悖论问题8、关于数学知识在物理上的应用探索9、投资人寿保险和投资银行的分析比较10、黄金数的广泛应用11、编程中的优化算法问题12、余弦定理在日常生活中的应用13、证券投资中的数学14、环境规划与数学15、如何计算一份试卷的难度与区分度16、数学的发展历史17、以“养老金”问题谈起18、中国体育彩票中的数学问题19、“开放型题”及其思维对策20、解答应用题的思维方法21、高中数学的学习活动——解题分析 A）从尝试到严谨、B）从一个到一类22、高中数学的学习活动——解题后的反思——开发解题智慧23、中国电脑福利彩票中的数学问题24、各镇中学生生活情况25、城镇/农村饮食构成及优化设计26、如何安置军事侦察卫星27、给人与人的关系（友情）评分28、丈量成功大厦29、寻找人的情绪变化规律30、如何存款最合算31、哪家超市最便宜32、数学中的黄金分割33、通讯网络收费调查统计34、数学中的最优化问题35、水库的来水量如何计算36、计算器对运算能力影响37、数学灵感的培养38、如何提高数学课堂效率39、二次函数图象特点应用40、D中线段计算41、统计溪美月降水量42、如何合理抽税43、南安市区车辆构成44、出租车车费的合理定价45、衣服的价格、质地、品牌，左右消费者观念多少？46、购房贷款决策问题篇二：《高中数学有效课堂教学》课题研究总结《高中数学有效课堂教学》研究总结摘要：有效教学强调：关注学生的进步或发展，关注教学效益，关注可测性或量化，要求教师具备一种反思的意识。

我采用了“问题情景——建立模型——探究——解释——应用——拓展”的模式展开教学，课后进行认真的反思关键词：有效教学；实践；有效性；反思；设想有效教学的理念源于20世纪上半叶西方的教学化运动，它强调的是：关注学生的进步或发展，关注教学效益，关注可测性或量化，要求教师具备一种反思的意识。

数学模型在证券投资中的运用引言：证券投资是一门涉及到风险和收益的复杂领域，可以通过对市场和资产进行分析来做出最佳的投资决策。

数学模型作为一种工具，在证券投资中发挥着重要的作用。

本文将探讨数学模型在证券投资中的运用，并介绍一些常见的数学模型。

一、数学模型在证券投资中的基本原理数学模型可以基于不同的假设和方法来进行建立。

常见的数学模型包括随机漫步模型、均值方差模型、马尔可夫模型等。

这些模型可以通过收集历史数据和市场信息来进行参数估计和预测。

通过数学模型，可以分析市场和资产的风险、收益和其他相关因素，帮助投资者找到最佳的投资策略。

二、常见的数学模型1.随机漫步模型：随机漫步模型是描述资产价格变动的一种基本模型。

该模型假设资产价格的变动是随机的，与过去的价格无关。

通过随机漫步模型，可以对资产价格的未来走势进行预测和分析。

2.均值方差模型：均值方差模型是一种经典的投资组合模型。

该模型通过计算资产的平均收益和方差，找到一种能够最大化收益和最小化风险的投资组合。

通过均值方差模型，可以帮助投资者制定合理的资产配置策略。

3.马尔可夫模型：马尔可夫模型是一种基于转移概率的模型，用于分析资产价格的未来走势。

该模型假设资产价格的变动只与前一时刻的价格相关。

通过马尔可夫模型，可以统计资产价格的状态转移概率，从而对未来走势进行预测。

4.蒙特卡洛模拟：蒙特卡洛模拟是一种基于随机数的模型。

该模型通过生成大量的随机数，模拟市场和资产价格的变动，从而对风险和收益进行评估和分析。

通过蒙特卡洛模拟，可以对不同的投资策略进行模拟和比较，选择最佳的投资策略。

三、数学模型在证券投资中的应用实例1.高频交易策略：高频交易是一种利用数学模型和算法进行快速交易的策略。

通过分析市场和资产的微小变动，利用数学模型来识别价格差异，并快速进行交易，从而获得利润。

高频交易策略依赖于数学模型的准确性和快速执行的能力。

2.风险控制：数学模型在风险控制中起着至关重要的作用。