竞赛力矩平衡(定轴问题)

第二讲 力平衡（一）精选例题【例1】 如图所示一个均匀的质量为1m 的球挂在天花板上，从同一点挂一个重物质量为2m 。

问所成角度。

O 【解析】相对于点的总力矩为0.)m g (l +R )sin =m 12g R -(l +R sin θθ⎡⎤⎣⎦∴()1212sin []+R m (m +)m R l θ-=该题如果用变力分析去解题，对悬挂2m 的绳对大球的支持力的方向比较困难，而用力矩去解题，显得尤为简单【例2】 如图，重为G 木块用绳子悬挂在两个轻杆支架的交点P ，现给木块一个水平方向的F F 12N 、N 、T 作用力，缓慢增大并且系统保持平衡，求作用力的变化趋势。

N 【解析】可以采用图解法，分别考虑木块以及P 点的受力平衡，将二者的受力三角形画在同一个图中，利用几何相似三角形的方法可以得到三个力的变化趋势。

最后可得，不变，2N 1和T 增加。

【例3】 如图，一个半径为R 非均匀质量光滑的圆球，其重心不在球心O 处，先将它置于A 30︒B A B 30︒C O 水平地面上，平衡时球面上的点和地面接触；再将它置于倾角为的粗糙斜面上，平衡时球面上的点与斜面接触，已知到的圆心角也为，试求球体的重心到球心的距离.【解析】B BC A OA 放在斜面上，球受重力支持力和摩擦力，三力共点必过点的重心在过B 于平面垂直的直线上。

即，又放在水平面上点落地，则此时球受重力和支持力，则球重心必在连线上，则重心位置在C 点.CO==【例6】有一长l重为W的均匀杆AB，A顶端竖直的粗糙墙壁上，杆端与墙间的摩擦系数μB CθμθP A P WPB PA x 为，端用一强度足够而不可伸长的绳悬挂，绳的另一端固定在墙壁点，木杆呈水平状态，绳与杆的夹角为（如图），求杆能保持平衡时与应满足的条件。

杆保持平衡时，杆上有一点存在，若与点间挂一重物，则足够大可以破坏平衡了，而在间任一点悬挂任意重物均不能破坏平衡。

求距离. 【解析】受力分析coT Nsθ=力平衡siT f W Wnθ+=+A力矩平衡：以为支点，θ=Wsin2lTl W+x∴f=W+W-N tan≤Nθμ2W xtanθ=+N W∴0002l2lW Wx xW+W Wtanlμθ-+()≤(+W)∴00()2l2W W)≤(+WtanlW Wx xμθ+-①0W=ntaμθ≥当不挂生物,此即为不挂重物平衡的条件，可得②W0(1)2tan(+1)-W Wμxμθl tanθ-+≤W取穷大，则上式仍成立.∴μθl tan(1)+-1tanxl tanθθμ+≥0⇒x≥wr G【例7】有一个半径为a，高为4a，重为的两端开口的薄壁圆筒，现将筒竖放在光滑的水平面上，之后将半径为，重为的两个完全相同的光滑圆球放入筒内而呈叠放状态，如图，当<r 2<a 2a 时，试求使圆筒不翻倒的条件.【解析】方法一：先看一个直角三角形O 对进行受力分析∴cos sin T =G cot θθ=N T θ=N G ⇒22212-a r ar -a r N =G ar -a sin θG =G =再对筒受力分析A N A 考虑以为支点，考虑翻倒则地面给筒的支持力的作用点移到点.则不翻倒条件。

力矩平衡力矩有固定转动轴物体的平衡(学案)教案(09)——力矩有固定转动轴物体的平衡考点解读教学目标1．知道力矩的定义，会求力矩．2．会求有固定转轴物体的平衡问题．教师归纳1．力矩(1)力臂：从转动轴到力的作用线(不是作用点)的垂直距离．(2)力矩：力F和力臂L的乘积叫作力对转动轴的力矩M，即M＝FL，力矩的单位是Nm. 2．物体的平衡态(1)物体保持静止或匀速直线运动状态．(2)物体绕固定转动轴匀速转动．3．有固定转动轴的物体的平衡条件：物体所受外力的力矩的代数和为零，即∑M＝0(或顺时针力矩之和等于逆时针力矩之和，即M顺＝M逆)．分类剖析(一) 如图所示，直杆OA可绕过O点的水平轴自由转动，图中虚线与杆平行，杆的另一端A点受到四个力F1、F2、F3、F4的作用，力的作用线与OA杆在同一竖直平面内，它们对转轴O的力矩分别为M1、M2、M3、M4，则它们间的大小关系是( )A．M1＝M2＞M3＝M4 B．M2＞M1＝M3＞M4 C．M4＞M2＞M3＞M1 D．M2＞M1＞M3＞M4【解析】将各力分解成沿杆方向和垂直于杆方向的两个力，只比较后者的力矩即可，选B.(二)如图(1)所示，均匀杆AC长2 m，重10 N，在竖直平面内，A端有水平固定转动轴，C端挂一重70 N的重物，水平细绳BD系在杆上B点，且AB＝3AC/4.要使绳BD的拉力是100N，则∠ABD ＝________；要使BD绳的拉力最小，且B点位置不变，改变BD的长度，则需BD与AC呈________状态．(1)(2)【解析】取AC杆为研究对象，以A为转轴，对AC杆产生转动作用的力是AC杆的重力G0、BD绳的拉力T、竖直向下的细绳的拉力F，F在数值上等于重力G；再由力矩的平衡条件∑M＝0求解．对AC受力分析如图(2)所示，由力矩的平衡条件1G0cosα＋FACcosα＝2T ABsinα1102cosα＋702cosα＝231002sinα4∴tanα＝1，α＝∠ABD＝45°因为重力的力矩、竖直向下的细绳拉力的力矩为一定值，若要使BD拉力最小，只有当拉力力臂最长时，即BD与AC呈垂直状态T最小.图中为南方少数民族常用的舂米工具．O为固定转动轴，重锤为A.脚踩在左端B处，可以使重锤升高，放开脚重锤落下打击稻谷．若脚用力方向始终竖直向下且转动保持平衡状态，则在重锤升起过程中，脚踩B端向下的力F和力矩M 将( )A．F增大，M增大B．F先增大后减小，M不变C．F不变，M先增大后减小D．F不变，M先减小后增大【解析】以O为轴，以舂米杠杆为研究对象，在重锤自下向上升起的过程中，重锤的力臂是先增大后减小，所以重锤的力矩先增大后减小．同时脚的力臂也是先增大后减小的，所以根据力矩的平衡条件，设杆与水平方向夹角为α，有mgAOcosα＝FBOcosαAO∴F＝mgBO无论杆在何位置F的大小始终不变．MF＝mgAOcosα，MF先增大后减小，所以正确答案选C.(三)一个质量为m＝50kg的均匀圆柱体，放在台阶的旁边，台阶的高度h是圆柱体半径r的一半，如图(1)所示(图为横截面)，柱体与台阶接触处图中P点，要在图中柱体的最上方A处施加一最小的力，使柱体刚能以P 为轴向台阶上滚(g取10m/s2)．求：(1)所加力的大小；(2)台阶对柱体的作用力的大小．(1) (2)【解析】(1)以P点为轴，欲在A处施最小的力，必须使这个力的力臂最长，那么该力的方向应垂直于PA，如图(2)所示．要使柱体刚能以P为轴向台阶上滚，即意味着此时地面对柱体的支持力恰好为零．这样由作用力F与重力mg对P点的力矩平衡可得mgBP ＝FAP 由几何关系得∠POB＝60°，∠PAO＝30°所以BP＝rsin60°，AP＝2rcos30°，解得F＝250N.(2)柱体刚能以P为轴向台阶上滚时，它受到在同一平面内三个非平行力的作用，即重力mg，作用在A点的外力F和台阶P点对柱体的作用力T.三力平衡必共点，据此可延长重力作用线与F交于A点，那么台阶对柱体的作用力T的延长线必定通过A点，即T的方向垂直于F的方向，所以T 的大小必等于重力在AP上的分力，因此有T＝mgcos30°＝433N.【点评】T是台阶P点对柱体的作用力，其指向球心的分力即为对柱体的支持力，而沿P点切线方向的分力则为对柱体的摩擦力．显然，对于光滑的接触点，是无法用此题给出的条件将柱体滚上台阶的.如图所示，OAB是一刚性轻质直角三角形支架，边长AB ＝0.2m，∠OAB＝37°；在A、B两顶角处各固定一个大小不计的小球，质量均为1kg.支架可绕过O的水平轴在竖直平面内无摩擦地转动．(sin37°＝0．6，cos37°＝0.8，重力加速度g取10m/s2)(1)为使支架静止时AB边水平，求在支架上施加的最小力；(2)若将支架从AB位于水平位置开始由静止释放，求支架转动过程中A处小球速度的最大值．【解析】施加的最小力满足的条件是：力臂最大，所以该力的作用点在A点，方向垂直OA向上mgOAcos37°＝mgOBcos53°＋FminOA OA＝0.16m，OB＝0.12m，可解得Fmin＝3.5N.(2)如图(1)(2)当支架到达平衡位置时，A球的速度最大，根据杠杆原理，此时A、B距O点垂线的距离相等，如图(2)所示，AE＝BD＝ABsin37°cos37°＝0.096mCD＝CEAC－AE＝0.028m OF＝ABsin37°cos37°＝AE h1＝OE－OF＝0.032m h2＝OF－OD＝0.024m11mg(h1－h2)v2＋m(vtan37°)222v＝质量M＝2.0kg的小铁块静止于水平轨道AB的A端．导轨及支架ABCD形状及尺寸如图所示，质量m＝4.0kg.它只能绕通过支架D点垂直于纸面水平转动，其中心在图中的O点，现有一细线沿导轨拉小铁块，拉力F＝12N，小铁块和导轨之间的动摩擦因数μ＝0.50.从小铁块运动时起，导轨(及支架)能保持静止的最长时间是多少？(g取10m/s2)【解析】当导轨刚要不能维持平衡时，C端受的力为零，此时导轨(及支架)受四个力作用：滑块对导轨的压力FN＝Mg，竖直向下，滑块对导轨的摩擦力Ff＝μMg＝10N，重力G＝mg，作用在O点，方向竖直向下，作用于轴D端的力．设此时的铁块走过的路程S，根据有固定转动轴物体平衡条件及图中尺寸，有：mg×0.1＋Mg(0.7－s)＝Ff×0.8＝μMg×0.8 40×0.1＋20(0.7－s)＝10×0.8 s＝0.5m铁块受的摩擦力Ff＝10N，方向向右．F－Ff＝Ma a＝1.0m/s2 ∵s＝1/2at2 ∴t＝1.0s【点评】此题是一道典型的力学综合题，考查面较广，从静力学，运动学到动力学，由于质量为m的铁块和T形支架不具有相同的运动状态，故必须采用隔离法．本章小结知识网络定义：力是物体对物体的作用，不能离开施力物体与受力使物体发生形变物体而存在概念 效果 改变物体运动状态要素：大小、方向、作用点（力的图示）效果：拉力、动力、阻力、支持力、压力 重力：方向、作用点（关于重心的位置）分类 性质 弹力：产生条件、方向、大小（胡克定律） 摩擦力：（静摩擦与动摩擦）产生条件、方向、大小力的合成运算——平行四边形定则 |F1－F2|≤F合≤F1＋F2力的分解 共点力作用下物体平衡物体平衡有固定转动轴物体平衡力考题解析考题1 如图所示，用两根细线把A、B两小球悬挂在天花板上的同一点O，并用第三根细线连接A、B两小球，然后用某个力F 作用在小球A上，使三根细线均处于直线状态，且OB细线恰好沿竖直方向，两小球均处于静止状态，则该力可能为图中的()A．F1 B．F2 C．F3 D．F4【解析】本题考查平衡物体的受力情况分析，属于基础知识．A、B两个小球用细线连接，且整个系统处在静止状态，在所提供的四个力中，能使系统保持静止的只能是F2和F3而不能是F1和F4，这是因为，若取F1，则F1可分解为水平向右和竖直向下两个分力，向下的分力将使A球向下运动，破坏了系统保持静止的前提；同样若取F4，则F4可分解为竖直向上和水平向左两个分力，向左的分力将使A球向左运动，且B球不再在竖直位置上．答案为选项B、C.考题 2 对如图所示的皮带传动装置，下列说法中正确的是( )A．A轮带动B轮沿逆时针方向旋转B．B轮带动A轮沿逆时针方向旋转C．C轮带动D轮沿顺时针方向旋转D．D轮带动C轮沿顺时针方向旋转【解析】本题主要考查考生灵活运用知识分析具体问题的能力．虽然涉力矩有固定转动轴物体的平衡(学案)及摩擦力概念，但重要的是如何运用摩擦力的概念分析与平常习题不同情境的问题．根据题目中呈示的图片，分别研究皮带绷紧的最高部分，结合摩擦力的概念，可以判断B、D为正确选项．考题 3 如图所示，在竖直平面内的直角坐标系中，一个质量为m的质点在外力F的作用下，从坐标原点O由静止沿直线ON斜向下运动，直线ON与y轴负方向成θ角(θ＜π/4)．则F大小至少为__________；若F＝mgtanθ，则质点机械能大小的变化情况是______________________________．【解析】考题考查力的最小值．该质点受到重力和外力F 从静止开始做直线运动，说明质点做匀加速直线运动，如图中显示，当F力的方向为a方向(垂直于ON)时，F力最小为mgsinθ；若F＝mgtanθ，即F力可能为b方向或c方向，故F力的方向可能与运动方向相同，也可能与运动方向相反，除重力外的F力对质点做正功，也可能做负功，故质点机械能增加、减少都有可能．考题4 如图所示，一根木棒AB在O点被悬挂起来，AO ＝OC，在A、C两点分别挂有两个和三个钩码，木棒处于平衡状态．如在木棒的A、C点各增加一个同样的钩码，则木棒DA．绕O点顺时针方向转动B．绕O点逆时针方向转动C．平衡可能被破坏，转动方向不定D．仍能保持平衡状态【解析】设木板AO段重力G1，重心离O点L1，木板BO段重力G2，重心离O点L2，AO长度l，由力矩平衡条件：G1L1＋2Gl ＝G2L2＋3Gl ，当两边各挂一个钩码后，等式依然成立：G1L1＋3Gl ＝G2L2＋4Gl ，即只要两边所增加挂钩码个数相同，依然能平衡．故选D.考题5 如图所示，半径分别为r和2r的两个质量不计的圆盘，共轴固定连结在一起，可以绕水平轴O无摩擦转动，大圆盘的边缘上固定有一个质量为m的质点，小圆盘上绕有细绳．开始时圆盘静止，质点处在水平轴O的正下方位置．现以水平恒力F拉细绳，使两圆盘转动，若恒力F＝mg，两圆盘转过的角度θ＝________时，质点m的速度最大．若圆盘转过的最大角度θ＝π/3，则此时恒力F＝________.1【解析】此题若用函数极值法，由动能定理有：mv2＝Frθ－mg(2r－2rcosθ)，可得2v＝2gr（θ＋2cos－2），然后求极值，很难求．换用力矩平衡条件，对盘、质点整体，π1以O为轴，当Fr＝mg2rsinθ时，转速最大即质点速度最大，得sinθ＝，所以有θ＝.当26πππ3mg圆盘转过最大角度θ＝时，由动能定理有2mgr(1－cos)＝0，可得F.333π百度搜索“就爱阅读”,专业资料,生活学习,尽在就爱阅读网,您的在线图书馆。

第一讲 平衡问题典题汇总类型一、物体平衡种类的问题一般有两种方法解题，一是根据平衡的条件从物体受力或力矩的特征来解题，二是根据物体发生偏离平衡位置后的能量变化来解题。

1、如图1—4所示，均匀杆长为a ，一端靠在光滑竖直墙上，另一端靠在光滑的固定曲面上，且均处于Oxy 平面内．如果要使杆子在该平面内为随遇平衡，试求该曲面在Oxy 平面内的曲线方程．分析和解：本题也是一道物体平衡种类的问题，解此题显然也是要从能量的角度来考虑问题，即要使杆子在该平面内为随遇平衡，须杆子发生偏离时起重力势能不变，即杆子的质心不变，y C 为常量。

又由于AB 杆竖直时12C y a =， 那么B 点的坐标为 sin x a θ=111cos (1cos )222y a a a θθ=-=- 消去参数得222(2)x y a a +-=类型二、物体系的平衡问题的最基本特征就是物体间受力情况、平衡条件互相制约，情况复杂解题时一定要正确使用好整体法和隔离法，才能比较容易地处理好这类问题。

例3．三个完全相同的圆柱体，如图1一6叠放在水平桌面上，将C 柱放上去之前，A 、B 两柱体之间接触而无任何挤压，假设桌面和柱体之间的摩擦因数为μ0，柱体与柱体之间的摩擦因数为μ，若系统处于平衡，μ0与μ必须满足什么条件？分析和解：这是一个物体系的平衡问题，因为A 、B 、C 之间相互制约着而有单个物体在力系作用下处于平衡，所以用隔离法可以比较容易地处理此类问题。

设每个圆柱的重力均为G ，首先隔离C 球，受力分析如 图1一7所示，由∑Fc y ＝0可得111)2N f G += ① 再隔留A 球，受力分析如图1一8所示，由∑F Ay =0得1121022N f N G +-+= ② 由∑F Ax =0得211102f N N -= ③ 由∑E A ＝0得12f R f R = ④ 由以上四式可得12f f ===112N G =，232N G =而202f N μ≤，11f N μ≤0μ≥2μ≥类型三、物体在力系作用下的平衡问题中常常有摩擦力，而摩擦力F f 与弹力F N 的合力凡与接触面法线方向的夹角θ不能大于摩擦角，这是判断物体不发生滑动的条件．在解题中经常用到摩擦角的概念．例4．如图1一8所示，有两根不可伸长的柔软的轻绳，长度分别为1l 和2l ，它们的下端在C 点相连接并悬挂一质量为m 的重物，上端分别与质量可忽略的小圆环A 、B 相连，圆环套在圆形水平横杆上．A 、B 可在横杆上滑动，它们与横杆间的动摩擦因数分别为μ1和μ2，且12l l <。

力矩转动平衡问题(总10页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第17讲 力矩 转动平衡问题1．力臂：从转轴到力的作用线的F 垂直距离．2．力矩：力F 与力臂上的乘积．即M=FL ，力矩的单位是N ·m3．作用：反映力对物体的转动效果，是使物体的转动状态发生改变的原因．4．力矩的平衡：有固定转动轴的物体的平衡条件是力矩和等于零．即∑M=0或∑M 逆=∑M 顺。

5．力矩的计算方法力对某转动轴的力矩，顺时针方向，规定为负力矩；逆时针方向，规定为正力矩．当力与转轴平行时，力对该轴没有力矩，当力与转动轴成任意角度时，力对这一转动轴的力矩，可将力分解为与轴平行和垂直的两个分力，垂直于轴的分力对轴的力矩也就是该力的力矩．6．有固定转动轴物体受力分析的要点：首先认准转动轴，只分析作用线不通过转动轴的力，因作用线过转动轴的力的力矩为零，对物体的转动不产生影响.作受力分析图时，力的作用点、作用线不能随意移动，这与用共点力的平衡研究问题时的受力分析图有一定区别，共点力平衡问题讨论的是物体的平动问题，可以把物体视为质点看待，画受力图强调的是方向问题，作用力的作用点，作用线不作要求．力矩的平衡问题讨论的是转动问题，物体不可以视为质点，则力的作用点，作用线要求准确，不能在物体上随意移动．7．一般物体的平衡对一般物体来说，其平衡条件必是满足∑F=0，对任意轴的力矩有∑M=0．8．利用力矩平衡条件解题的一般程序是：(1)确定研究对象，即明确要研究哪一个物体的转动趋势．(2)确定转动轴．转动平衡物体的转轴理论可任意选择，选轴的一般原则：使未知力尽可能多地通过轴，以减少方程数．(3)对研究对象进行受力分析，并作出受力示意图．(4)根据受力分析，确定每一个力对转动轴的力臂．(5)计算每一个力对转动轴的力矩，并确定各个力矩的正、负号．(6)根据力矩平衡列方程．必要时要根据题给条件列出辅助方程．(7)求解方程，并对所求结果进行必要的讨论，（一）力矩概念的考查1．.如图所示，直杆OA 可绕O 点转动，图中虚线与杆平行，杆端A 承受两个力F 1、F 2的作用，力的作用线跟OA 杆在同一竖直面内，它们对转轴O 的力距分别是M 1、M 2，则力矩间的大小关系是( )．A ．M 1> M 2B ．M 1= M 2C ．M 1< M 2D ．无法推断2．如图所示直杆OA可绕O点转动，图中虚线与杆平行，杆端A点受四个力F1、F2、F3、F4的作用,图中力矢量的长短表示力的大小，力的作用线跟OA杆在同一平面内，它们对转轴O的力矩分别为M1、M2、，则力矩间的大小关系为 ( )A．M1= M2= M3= M4 B．M2> M1= M3> M4C. M1> M2> M3> M4； D．M2> M1> M4> M33．质量分布均匀，边长为a的正方体，重力为G．在与水平成α=450角的力F作用下将绕边棱M翻转，此时正方体共受4个力作用，如图1—117所示，请说明各个力的力矩大小．4．如图所示，重为G的均匀立方体A端支在竖直墙的凸处，C端被一轻绳固定，绳的另一端固定在竖直墙上。

郑梁梅高级中学高一物理竞赛辅导讲义第三讲：力矩、定轴转动物体的平衡条件、重心【知识要点】（一）力臂：从转动轴到力的作用线的垂直距离叫力臂。

（二）力矩：力和力臂的乘积叫力对转动轴的力矩。

记为M=FL ，单位“牛·米”。

一般规定逆时针方向转动为正方向，顺时针方向转动为负方向。

（三）有固定转轴物体的平衡条件作用在物体上各力对转轴的力矩的代数和为零或逆时针方向力矩总是与顺时针方向力矩相等。

即ΣM=0，或ΣM 逆=ΣM 顺。

（四）重心：物体所受重力的作用点叫重心。

计算重心位置的方法：1、同向平行力的合成法：各分力对合力作用点合力矩为零，则合力作用点为重心。

2、割补法：把几何形状不规则的质量分布均匀的物体分割或填补成形状规则的物体，再由同向（或反向）平行力合成法求重心位置。

3、公式法：如图所示，在平面直角坐标系中，质量为m 1和m 2的A 、B 两质点坐标分别为A （x 1，y 1），B （x 2，y 2）则由两物体共同组成的整体的重心坐标为： 212211m m x m x m x C ++= 212211m m y m y m y C ++= 一般情况下，较复杂集合体，可看成由多个质点组成的质点系，其重心C 位置由如下公式求得：i i i C m x m x ∑∑= i i i C m y m y ∑∑= ii i C m z m z ∑∑= 本节内容常用方法有：①巧选转轴简化方程：选择未知量多，又不需求解结果的力线交点为轴，这些力的力矩为零，式子简化得多；②复杂的物体系平衡问题有时巧选对象：选整体分析，常常转化为力矩平衡问题求解；③无规则形状的物体重心位置计算常用方法是通过割补思想，结合平行力合成与分解的原则处理，或者助物体重心公式计算。

【典型例题】【例题1】如图所示，光滑圆弧形环上套有两个质量不同的小球A 和B 两球之间连有弹簧，平衡时圆心O 与球所在位置的连线与竖直方向的夹角分别为α和β，求两球质量之比。

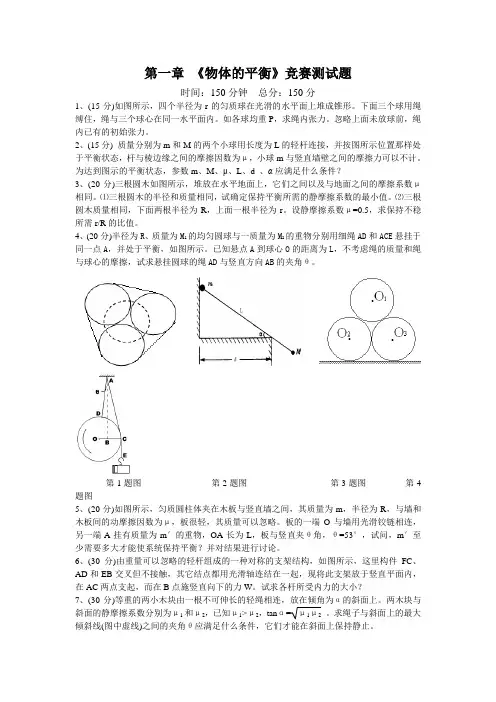
第一章《物体的平衡》竞赛测试题时间：150分钟总分：150分1、(15分)如图所示，四个半径为r的匀质球在光滑的水平面上堆成锥形。

下面三个球用绳缚住，绳与三个球心在同一水平面内。

如各球均重P，求绳内张力。

忽略上面未放球前，绳内已有的初始张力。

2、(15分) 质量分别为m和M的两个小球用长度为L的轻杆连接，并按图所示位置那样处于平衡状态，杆与棱边缘之间的摩擦因数为μ，小球m与竖直墙壁之间的摩擦力可以不计。

为达到图示的平衡状态，参数m、M、μ、L、d 、α应满足什么条件？3、(20分)三根圆木如图所示，堆放在水平地面上，它们之间以及与地面之间的摩擦系数μ相同。

⑴三根圆木的半径和质量相同，试确定保持平衡所需的静摩擦系数的最小值。

⑵三根圆木质量相同，下面两根半径为R，上面一根半径为r。

设静摩擦系数μ=0.5，求保持不稳所需r/R的比值。

4、(20分)半径为R、质量为M1的均匀圆球与一质量为M2的重物分别用细绳AD和ACE悬挂于同一点A，并处于平衡，如图所示。

已知悬点A到球心O的距离为L，不考虑绳的质量和绳与球心的摩擦，试求悬挂圆球的绳AD与竖直方向AB的夹角θ。

第1题图第2题图第3题图第4题图5、(20分)如图所示，匀质圆柱体夹在木板与竖直墙之间，其质量为m，半径为R，与墙和木板间的动摩擦因数为μ，板很轻，其质量可以忽略。

板的一端O与墙用光滑铰链相连，另一端A挂有质量为m′的重物，OA长为L，板与竖直夹θ角，θ=53°，试问，m′至少需要多大才能使系统保持平衡？并对结果进行讨论。

6、(30分)由重量可以忽略的轻杆组成的一种对称的支架结构，如图所示，这里构件FC、AD和EB交叉但不接触，其它结点都用光滑轴连结在一起，现将此支架放于竖直平面内，在AC两点支起，而在B点施竖直向下的力W。

试求各杆所受内力的大小？7、(30分)等重的两小木块由一根不可伸长的轻绳相连，放在倾角为α的斜面上。

两木块与斜面的静摩擦系数分别为μ1和μ2，已知μ1>μ2，tanα=μ1μ2。

高中物理竞赛力矩和力矩平衡知识点讲解力矩是表示力对物体产生转动作用的物理量，是物体转动转动状态改变的原因。

它等于力和力臂的乘积。

表达式为：M=FL，其中力臂L是转动轴到F的力线的（垂直）距离。

单位：Nm 效果：可以使物体转动.正确理解力矩的概念力矩是改变转动物体的运动状态变化的物理量，门、窗等转动物体从静止状态变为转动状态或从转动状态变为静止状态时，必须受到力的作用。

但是，我们若将力作用在门、窗的转轴上，则无论施加多大的力都不会改变其运动状态，可见转动物体的运动状态的变化不仅与力的大小有关，还受力的方向、力的作用点的影响。

力的作用点离转轴越远，力的方向与转轴所在平面越趋于垂直，力使转动物体运动状态变化得就越明显。

物理学中力的作用点和力的作用方向对转动物体运动状态变化的影响，用力矩这个物理量综合表示，因此，力矩被定义为力与力臂的乘积。

力矩概括了影响转动物体运动状态变化的所有规律，力矩是改变转动物体运动状态的物理量。

力矩是矢量，在中学物理中，作用在物体上的力都在同一平面内，各力对转轴的力矩只能使物体顺时针转动或逆时针转动，这样，求几个力矩的合力就简化为代数运算。

力对物体的转动效果使物体转动改变的效果不仅跟力的大小有关，还跟力臂有关，即力对物体的转动效果决定于力矩。

①当臂等于零时，不论作用力多么大，对物体都不会产生转动作用。

②当作用力与转动轴平行时，不会对物体产生转动作用，计算力矩，关键是找力臂。

需注意力臂是转动轴到力的作用线的距离，而不是转动轴到力的作用点的距离。

大小一定的力有最大力矩的条件：①力作用在离转动轴最远的点上；②力的方向垂直于力作用点与转轴的连线。

力矩的计算：①先求出力的力臂，再由定义求力矩M＝FL如图中，力F 的力臂为LF=Lsin θ 力矩M ＝F •L sin θ②先把力沿平行于杆和垂直于杆的两个方向分解，平行于杆的分力对杆无转动效果，力矩为零；平行于杆的分力的力矩为该分力的大小与杆长的乘积。

专题一力物体的平衡第一讲力的处理矢量的运算1、加法表达：a + b = c o名词：c为“和矢量”。

法则：平行四边形法则。

如图1所示和矢量大小：c = a2b22abco^ ，其中a为a和b的夹角。

和矢量方向：c在a、b之间，和a夹角B = arcs in ------2 2.a b 2abcos:-2、减法表:达：a = c — b o名词：c为“被减数矢量”，b为“减数矢量”，a为“差矢量”法则：三角形法则。

如图2所示。

将被减数矢量和减数矢量的起始端平移到一点，然后连接两时量末端，指向被减数时量的时量，即是差矢量。

差矢量大小：a = ；b2• c2- 2bccosr，其中B为c和b的夹角。

差矢量的方向可以用正弦定理求得。

一条直线上的矢量运算是平行四边形和三角形法则的特例。

例题：已知质点做匀速率圆周运动，半径为R，周期为T，求它在-T内和4 1在-T内的平均加速度大小。

21解说：如图3所示，A到B点对应-T的过程，A4到C点对应1T的过程。

这三点的速度矢量分别设为2v A、v B和 v C。

图3_v t —V 。

/曰 __V B —V A . _v c —V A a =得：a AB = , a Ac =-tt ABt AC由于有两处涉及矢量减法，设两个差矢量.：V 1= V B — V A ，厶v 2= v c — V A ,根据三角形法则，它们在图3中的大小、方向已绘出（：V2的“三角形”已被拉 伸成一条直线）。

本题只关心各矢量的大小，显然：V A = V B = V c = 2JI R且.T■：v 1 = . 2 v A =2 2二 RTL V2 = :2 V A =4 二 R 'T2 2 二R4二 R所以： a AB =v 1 _ T =8 2 二Ra■ A V 2T - 8二 Rt ABT T 2ACt ACT T 242观察与思考：这两个加速度是否相等，匀速率圆周运动是不是匀变速运动? 答：否；不是。

一、（40分）如图1a ，一段抛物线形状的刚性金属丝固定在竖直平面内，抛物线方程为y = ax 2（y 轴竖直向上，a 为待定常量）；一长度为2l 的匀质刚性细杆的两端A 、B 各有一个小圆孔，两圆孔都套在金属丝上。

圆孔和金属丝之间非常光滑，摩擦力非常小，在问题（1）、（2）和（3）中可忽略。

若给细杆一个冲量，使其运动；经过足够长的时间，细杆静止于平衡位置，此时细杆和水平方向之间的夹角=︒θ30。

已知重力加速度大小为g 。

（1）求待定常量a ；（2）若杆在上述平衡位置附近小幅振动，求振动的频率；（3）细杆静止在上述平衡位置。

现有一只小白鼠，从静止开始由杆底端沿杆往上爬。

在爬杆的过程中，细杆始终保持静止；假设小白鼠可视为质点，且小白鼠在杆端不接触金属丝。

求小白鼠在时刻t （以小白鼠开始爬杆的时刻为时刻零点）沿细杆的位移s t ()，小白鼠是否可以爬到细杆顶端？如果可以，小白鼠爬到细杆顶端，最少用时多少？解答：（1）设细杆的质心的坐标为（x c ，y c ），细杆的长度为2l ，则杆的A 和B 端的坐标为：① 2分代入抛物线方程得：② ③联立②③式得：④ 1分⑤ 1分细杆重力势能为：⑥ 2分平衡点为势能极值点：⑦ 2分解为：I 、 sin θ =0，即θ =0，不符题意，舍去。

⑧ II 、⑨得：⑩已知θ=30°，所以：⑪图1a B 第39届全国中学生物理竞赛决赛理论考试试题⑫ 2分（2）细杆在平衡位置附近小幅振动，由机械能守恒得：⑬ 4分即：⑭ 2分令：θ=θ0+∆θ（|∆θ|≪θ0），θ0=30°为平衡位置，于是⑭式在θ0附近做小量∆θ展开，并且质心动能、相对质心转动动能和势能三部分都保留至（不是常量的）最大一项，得到近似式：⑮ 6分两边对时间求导得：⑯ 2分或小幅振动可以近似为简谐运动，角频率为：⑰振动频率：⑱ 2分（3）设白鼠的质量为m s，沿细杆的位移为s，B点s=0，加速度为d2s/dt2，则白鼠对细杆的作用力：，竖直向下；2 22sd sF mdt=，沿细杆。

高中物理竞赛—静力学知识要点分析一、力的效应1．内、外效应：力的作用效果有两种：一是受力物发生形变；二是使受力物的运动状态发生变化。

前者表现为受力物各部分的相对位置发生变化，故称为力的内效应；后者表现为受力物的运动方向或快慢发生变化，故称为力的外效应。

众所周知，当物体同时受到两个或多个力作用时，它的运动状态也可能保持不变，这说明力对同一物体的外效应可能相互抵消。

2．合力与分力合力与它的那组分力之间，在力学效果上必须具有“等效代换”的关系。

二、力的作用方式力是物体间的一种相互作用，又是一并具有大小、方向和作用点的一种矢量。

根据研究和解决实际问题的需要，可以从不同的角度对力进行区分。

1．体力、面力和点力按照力的作用点在受力物上的分布情况，可将力可将力分为体力、面力和点力三种。

外力的作用点连续分布在物体表面和内部的一定（或全部）区域，这种力就是体力。

重力就是一种广泛存在的体力。

作用点连续分布在物体某一面（或全部表面）上，这种力就是面力。

压力和摩擦力就是一种广泛存在的面力。

当面力和体力作用的区域远比受力物小,或可以不考虑作用点的分布情况时,就可以把相应的体力或面力当成是集中在物体的某一点上作用的,这种情况下的体力和面力就叫做点力。

例如,在通常情况下,我们就是把重力、摩擦力和压力当成点力看待。

具体而言,常用物体各部分所受重力的合力来代替该物体受到的总重力；用摩擦面上各部分所受摩擦力之合力来代替这个面上的总摩擦力；对压力也是按照这种方式处理的。

当不涉及转动的时候,我们甚至把面力的合力作用点标出在物体的重心上，这就使问题的解决更加便当。

但若涉及到物体的转动,就绝对不能把体力和面力（如磁力）的作用点随便地集中到物体的重心上。

点力只是在一定条件下对体力和面力的一种适当的简化而已，对此切勿掉以轻心。

2．内力和外力按照施力物与被研究物体的所属关系，又常将力分为内力和外力两大类若被研究对象是某一物体，则该物体内部各部分间的作用力叫内力；若被研究对象是两个或多个物体组成的系统，则系统内部各物体间的作用力都叫该系统的内力。

力矩平衡条件的应用力矩平衡基础例1如图：BO 是一根质量均匀的横梁，重量G 1＝80N ，BO 的一端安在B 点，可绕通过B 点且垂直于纸面的轴转动，另一端用钢绳AO 拉着横梁保持水平，与钢绳的夹角o 30=θ，在横梁的O 点挂一个重物，重要G 2＝240N ，求钢绳对横梁的拉力F 1：例2如图所示，OAB 是一弯成直角的杠杆，可绕过O 点垂直于纸面的轴转动，杆OA 长30cm ，AB 段长为40cm ，杆的质量分布均匀，已知OAB 的总质量为7kg ，现在施加一个外力F ，使杆的AB 段保持水平，则该力作用于杆上哪一点，什么方向可使F 最小？例3一辆汽车重1.2×104N ，使它的前轮压在地秤上，测得的结果为6.7×103N ，汽车前后轮之间的举例是2.7m ，求汽车重心的位置，（即求前轮或后轮与地面接触点到重力作用线的距离）力矩平衡初步例1一块均匀木板MN 长L ＝15cm ，G 1＝400N ，搁在相距D ＝8m 的两个支架A 、B 上，MA ＝NB ，重G 2＝600N 的人从A 向B 走去，如图：问人走过B 点多远时，木板会翘起来？例2如图3-3所示，长为L 质量为m 的均匀木棒，上端用绞链固定在物体上，另一端放在动摩擦因数为μ的小车平台上，小车置于光滑平面上，棒与平台的夹角为θ，当：（1）小车静止时，求棒的下端受小车的支持力；（2）小车向左运动时，求棒的下端受小车的支持力；（3）小车向右运动时，求棒的下端受小车的支持力.练习1如图所示，均匀直杆AB 的A 端装有垂直于纸面的水平转动轴，B 端搁在小车上，杆与车的水平上表面间滑动摩擦系数为μ，小车静止时，杆对车的压力大小为N1.当小车水平向左运动时，杆对车的压力大小为N2，则 ( )A.N1＝N2.B.N1＜N2.C.N1＞N2.D.无法确定.图练习2如图所示，重200N 的均匀杆OA ，可绕过O 点的水平轴自由转动，杆斜靠在竖直墙上，杆与水平面间的夹角θ＝60°，墙与杆间夹有一张纸，纸的重及纸与墙间的摩擦力不计，纸与杆间的滑动摩擦系数μ＝0.2.问要多大的竖直向上的力才能将纸向上匀速抽出?练习3右图所示是用电动砂轮打磨工件的装置，砂轮的转轴通过图中O 点垂直于纸面，AB 是一长度l=0.60m 、质量m1=0.50kg 的均匀刚性细杆，可绕过A 端的固定轴在竖直面(图中纸面)内无摩擦地转动，工件C 固定在AB 杆上，其质量m2=1.5kg ，工件的重心、工件与砂轮的接触点P 以及O 点都在过AB 中点的竖直线上，P 到AB杆的垂直距离d=0.1m ，AB 杆始终处于水平位置，砂轮与工件之间的动摩擦因数μ=0.6.(1)当砂轮静止时，要使工件对砂轮的压力F0=100N ，则施于B 端竖直向下的力FB 应是多大?(2)当砂轮逆时针转动时，要使工件对砂轮的压力仍为F0=100N ，则施于B 端竖直向下的力FB′应是多大?练习4如图所示是一种手控制动器，a 是一个转动着的轮子，b 是摩擦制动片，c 是杠杆，O 是其固定转动轴。

第二章 力和物体的平衡【竞赛要求】摩擦力 弹性力 胡克定律 共点力作用下物体的平衡 力矩 刚体的平衡条件 重心 物体平衡的种类第一节 力的合成与分解 力学理想模型一、刚体 1、基本概念刚体就是在任何情况下形状和大小都不发生变化的物体。

刚体是一种理想化的力学模型，当实际物体的形变对所研究问题的影响可以忽略时，就可将物体看成刚体。

讨论刚体力学时，常把刚体分成许多部分，每一部分都小到可看成质点，这些小部分 叫做刚体的“质元”。

由于刚体不变形，各质元间的距离不变，质元间距离保持不变的质点组叫做“不变质点组”，把刚体看作不变质点组并运用已知质点或质点组的运动规律加以讨论，这是刚体力学的基本方法。

通常把作用于刚体的若干个力称为力系，若作用于刚体的力系不影响刚体的运动状态，这样的力系称作平衡力系。

如果用一个力系代替作用于刚体上的另一个力系时，力的作用效果没有变化，即刚体的状态不变，则称此二力系为等效力系。

与力系等效的力称为合力。

2、重要规定和结论：加减平衡力系原理：在作用于刚体上的已知力系中，加上或去掉任何一个平衡力系，并不改变原力系对刚体的作用效果，即不改变刚体的状态(运动状态或静止状态)。

力的可传性原理：作用于刚体上的力，其作用点可沿作用线移至刚体内任一点，而不改变该力对刚体的作用效果。

二、力的合成与分解：1、平行四边形定则，三角形定则，多边形定则2、平行力的合成：什么叫做共点力(系)，什么叫做平行力(系)同向平行力的合成：两个同向平行力F A 和F B 相距AB ，则合力F 的大小为F A +F B ，合力的方向与两个分力相同，合力的作用线与AB 的交点为C ，且满足F A •AC=F B •BC 的关系(如下左图所示)。

反向平行力的合成：两个大小不同的反向平行力F A 和F B (F A >F B )相距AB ，则合力F 的大小为F A -F B ，与F A 同向，合力的作用线与AB 延长线上靠近A 的一侧交点为C ，且满足F A •AC=F B •BC 的关系。

学案8：力矩有固定转动轴物体的平衡【学习目标】1．理解力臂、力矩的概念；2．能正确找出给定力的力臂，并运用公式M＝FL解决实际的力矩问题；3．知道当力的作用线垂直于“力的作用点与转轴连线”时，其力臂最大；4．掌握有固定转动轴的物体的平衡条件，会应用力矩平衡条件处理有关问题。

【课堂讲练】◆思考：生活中，我们常见到使物体发生转动的例子，比如用手推开门、用扳手拧螺帽、用铁棒撬开路面上的障碍物等等，那么在这些转动中，你认为有哪些因素决定了物体的转动效果呢？◆学生活动：用手推开门时，分别改变力的大小、方向、作用点，比较转动效果。

●小结：物体的转动效果1、力臂（L）：（1）定义：从到力的的垂直距离。

（2）单位：。

（3）大小特点：①当力沿何方向时，其力臂达最大？★当力于“与的连线”时，其力臂最大。

②当力沿何方向时，其力臂为零？★当力的作用线通过时，其力臂为零。

〖例1〗如图所示，O点为杆OB的转轴，请分别作出图中力F1、F2、F3的力臂。

2、力矩（M）：（1）定义: 力与力臂的乘积叫做力矩。

（2）定义式：M = F·L （M——力矩，F——作用力；L——力臂。

）（3）单位：_______ 。

（4）作用效果：使物体发生。

力矩越，物体的转动效果越明显；当力矩为时，物体不会发生转动。

（5）力矩的方向性：根据使物体转动的方向不同，力矩可分为顺转力矩和逆转力矩两种。

★使物体顺转的力矩，称为顺时针力矩；使物体逆转的力矩，称为逆时针力矩。

〖例2〗下图显示了用板手拧螺帽的几种情况。

在这些情景中，力的大小相同，均为30N，力的方向分别与扳手柄垂直(a、b)或成一夹角600(c)。

力的作用点与螺帽中心的距离OA分别为12cm(a、c)和20cm(b)。

求这些情况下F的力矩各是多少？3、有固定转动轴物体的平衡：（1）有固定转轴物体的平衡状态：匀速转动或静止不转。

（2）演示实验研究：①实验装置：如右图所示，力矩盘是均匀的，其重心在圆盘的中心，圆盘可以在竖直面内绕过中心的水平轴几乎无摩擦地转动。