初中数学青岛版九年级上册高效课堂资料3.5三角形的内切圆 学案

青岛版数学九年级上册3.5《三角形的内切圆》教学设计一. 教材分析《三角形的内切圆》是青岛版数学九年级上册3.5的内容。

本节课主要让学生掌握三角形的内切圆的定义、性质及求法，并能运用内切圆解决一些与三角形有关的问题。

教材通过实例引入内切圆的概念，引导学生探究内切圆的性质，最后通过例题和练习题巩固所学知识。

二. 学情分析学生在学习本节课之前，已经掌握了相似三角形的性质、圆的性质等知识。

但内切圆是一个较为抽象的概念，学生可能难以理解。

因此，在教学过程中，教师需要善于利用生活中的实例、模型等直观教具，帮助学生建立直观的形象，降低学习难度。

三. 教学目标1.了解三角形的内切圆的定义、性质及求法。

2.能运用内切圆解决一些与三角形有关的问题。

3.培养学生的空间想象能力、逻辑思维能力和解决问题的能力。

四. 教学重难点1.内切圆的定义及其性质。

2.内切圆在解决问题中的应用。

五. 教学方法1.情境教学法：通过生活实例引入内切圆的概念，激发学生的学习兴趣。

2.启发式教学法：在探究内切圆性质的过程中，引导学生主动思考、提问。

3.实践操作法：让学生动手操作模型，加深对内切圆的理解。

4.小组合作学习：引导学生分组讨论，培养学生的团队协作能力。

六. 教学准备1.准备内切圆的相关模型、图片等直观教具。

2.设计好PPT，展示教学过程和例题。

3.准备练习题，巩固所学知识。

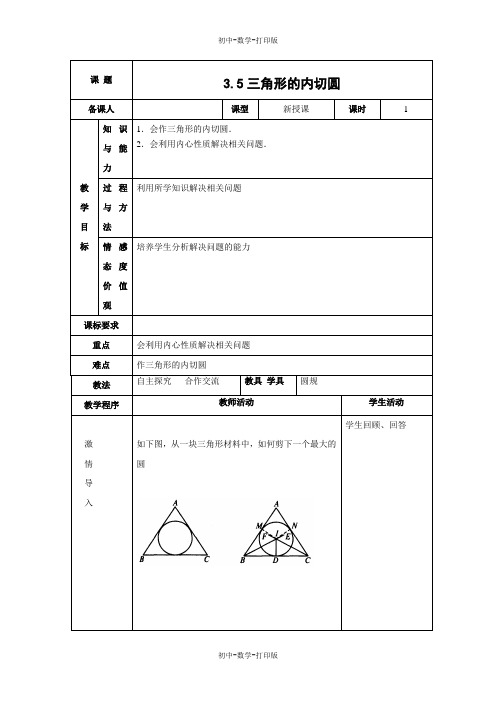
七. 教学过程1.导入（5分钟）利用生活中的实例，如花园里的花坛、水果店的苹果摆放等，引导学生思考：为什么这些形状看起来很协调？引入三角形的内切圆的概念，让学生初步了解内切圆。

2.呈现（10分钟）通过PPT展示内切圆的定义、性质及求法。

让学生直观地感受内切圆的特点，并引导学生思考如何求一个三角形的内切圆。

3.操练（10分钟）让学生分组讨论，每组选择一个三角形，尝试求出它的内切圆。

教师巡回指导，解答学生的疑问。

4.巩固（10分钟）出示一些练习题，让学生独立完成。

题目可以包括求三角形的内切圆半径、判断一个图形是否为某三角形的内切圆等。

BCAMNOA ．三角形的内心到三角形三个顶点的距离相等B ．三角形的内心不一定在三角形的内部C ．等边三角形的内心，外心重合D ．一个圆一定有唯一一个外切三角形2．在Rt △ABC 中，∠C=90°，AC=3，AB=5，则它的内切圆与外接圆半径分别为（ ）A ．1.5，2.5B ．2，5C ．1，2.5D ．2，2.5 3. 如果等边三角形的边长为a ，那么它的内切圆半径为（ ）A ．B ．a C ． a D ． a4.圆外一点引圆的两条切线互相垂直，这点与圆心的距离为4，则此圆的半径长为 .5.菱形ABCD 中，周长为40，∠ABC=120°，则内切圆的半径为____________.6.⊙O 是△ABC 的内切圆，D 、E 、F 是切点，∠A=50°，∠C=60°，则∠DOE 的度数是多少？四、变式训练，提升能力7.△ABC 中，E 是内心，∠A 的平分线和△ABC 的外接圆相交于点D. 求证：DE=DB.五、当堂检测1.下列图形中，一定有内切圆的四边形是（ ）DABCE（A）梯形（B）菱形（C）矩形（D）平行四边形2.正三角形的内切圆半径、外接圆半径和高的比为（）A．1∶2∶3 B．2∶3∶4 C．1∶∶ D．1∶∶23.正三角形内切圆与外接圆周长的比是（）A．1∶ B．1∶2 C．1∶3 D．1∶4. 已知三角形的三边a＝3，b＝4，c＝5，则它的内切圆的半径r＝________．5.如图，等边三角形ABC的内切圆的面积为9π，则△ABC的周长为________．6.设等边三角形的内切圆半径为r，外接圆半径为R，边长为a，则r︰R︰a＝________．7.锐角ΔABC中，∠B=80°，I是ΔABC的内心，则∠AIC=______________.8.直角三角形一直角边长为6，斜边上的高为4．8，则其内切圆面积为__________．六、小结，作业1、小结2、作业：必做题：习题课后拓展案已知⊙O为△ABC的内切圆，D、E、F为切点，则△DEF一定是________三角形．。

3.5三角形的内切圆【学习目标】1.了解三角形的内切圆相关的概念2.能利用三角形内心的性质进行证明和计算【教材重点】三角形的内切圆相关的概念【教材难点】用三角形内心的性质进行证明和计算课前预习【温故知新】1、什么叫三角形的外接圆？什么叫圆的内接三角形？什么叫三角形的外心？2、思考：⑴如何求作三角形的外心⑵三角形的外心有何性质:3、角平分线上的点到，到角两边距离相等的点在课内助学【试一试】如图是一块三角形木料，木工师傅要从中裁下一块圆形用料，怎样才能使裁下的圆的面积尽可能大呢？【探索新知】OAB活动一:思考、操作(1) 图一,在∠AOB 内作圆，使其与两边OA 、OB 都相切,满足上述条件的圆是否可以作出？ 如果可以作出,能作多少个?所作出的圆的圆心的位置有什么特征？你是如何确定圆的半径的？(2) 图二，在△ABC 内作圆，使其与各边都相切,满足上述条件的圆是否可以作出,如果可以作出,能作多少个?所作出的圆的圆心是如何确定的?半径是如何确定的?请在图中作出△ABC 的内切圆。

活动二:自学并思考：自学课本101-102页，完成下面问题：1、什么叫三角形的内切圆？什么叫圆的外接三角形?什么叫三角形的内心？2、三角形的内心的性质 活动三：讨论填表：名称 确定方法 图形 性质外心BCA BCEABCE内心【精讲点拨】例一：在△ABC 中,∠A=68°,点E 是内心。

求∠BEC 的度数。

巩固训练：1。

如图，点E 是△ABC 的内心，若∠BEC ＝140°则∠A 的度数为2.已知在△ABC 中，∠A=40°，∠B=70°,点I 是△ABC 的内心。

求∠AIB,∠BIC 和∠AIC 的度数.【探讨1】：设△ABC 的内切圆的半径为r ，△ABC 的各边长之和为C ，△ABC 的面积S ，我们会有什么结论? 【探讨2】:如图，直角三角形的两直角边分别是a,b ，斜边为c 则其内切圆的半径ｒ为: (以含ａ、ｂ、ｃ的代数式表示ｒ）【课堂小结】课末测学【当堂检测】1、⊙O 是边长为2的等边△ABC 的内切圆，则⊙O 的半径为 .第1题2、⊙O 是△ABC 的内切圆,与AB 、BC 、CA 分别相切于D 、E 、F ，∠DEF=45°。

《三角形的内切圆》教案探究版一、教学目标知识与技能1．理解三角形内切圆的有关概念，会作三角形的内切圆．2．掌握三角形内心的概念及性质，会利用内心的性质求一些角度的度数．过程与方法1．让学生经历自己画图、类比、分析的过程，深刻理解三角形内切圆的概念及内心的性质．2．通过观察、实验、猜想、验证、推理、交流等数学活动，进一步发展学生的演绎推理能力和发散思维．情感、态度1．在简单的操作活动中，发展学生的说理意识和主动探究的习惯，同时培养学生的合作意识和交流能力．2．让学生在动手、动脑主动参与课堂教学活动的过程中体会知识间的联系，激发学生的学习兴趣．二、教学重点、难点重点：掌握三角形内切圆的画法，理解三角形内切圆的有关概念．难点：画钝角三角形的内切圆．三、教学过程设计（一）复习引入已知△ABC，作出它的三条内角的平分线，并说说它们具有什么性质？师生活动：教师出示问题，学生作出该三角形的三条内角的平分线，并口述它们具有的性质．老师点评：1．在黑板上作出△ABC的三条内角平分线（简单回顾角平分线的作法），并口述其性质：①三条角平分线相交于一点；②交点到三条边的距离相等．今天我们将利用角平分线的性质来深入地研究直线与圆相切的情况．设计意图：回顾前面学过的知识，为新课作准备．（二）探究新知实验与探究（1）任意作一个∠AOB（如下图），如果在∠AOB内作圆，使其与两边OA，OB都相切，满足上述条件的圆是否可以作出？如果可以作出，能作多少个？所作出的圆的圆心的位置有什么特征？AOB师生活动：教师让学生先动手画图，然后分组讨论，最后得出结果．答：满足上述条件的圆可以作出，并且可以作无数个．其中每个圆的圆心到∠AOB的两边的距离都分别相等，所以这些圆的圆心都在∠AOB的平分线上．（2）任意作一个△ABC，如果在△ABC内作圆，使其与各边都相切，满足上述条件的圆是否可以作出？如果可以作出，能作多少个？所作出的圆的圆心的位置有什么特征？师生活动：教师让学生先动手画图，然后分组讨论，最后得出结果．答：通过画图得出：满足上述条件的圆可以作出，且只能作出一个，所作出的圆的圆心的位置到各边的距离都相等．（3）怎样用尺规作一个圆，使它与△ABC的各边都相切呢？师生活动：教师先让学生写出已知、求作，然后讨论作图方法，教师分析、引导：因为角平分线上的点到角的两边的距离相等，所以要求作的圆的圆心应是△ABC三个内角平分线的交点，最后师生共同完成作图过程．已知：△ABC（如图）．求作：⊙I，使它与△ABC各边都相切．作法：①作∠B ，∠C 的平分线BD ，CE ，BD 与CE 相交于点I （如下图所示）； ②过点I 作IF ⊥BC ，垂足为点F ；③以I 为圆心，IF 为半径作圆．⊙I 就是所求作的圆．（4）你能说出上面作图的道理吗？与三角形各边都相切的圆有几个？师生活动：教师出示问题，学生思考、讨论，教师找学生代表回答，然后订正． 因为角平分线上的点到角两边的距离相等，且三角形三条角平分线交于一点，所以在上图中以I 为圆心，IF 为半径作圆，该圆与△ABC 的各边都相切．由上面的作图过程可知，与三角形的各边都相同的圆能作并且只能作出一个．教师讲解：与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．注意：三角形的内心是三角形的三条角平分线的交点，它到三角形各边的距离相等．任何一个三角形都有且只有一个内心，三角形的内心在三角形的内部．设计意图：用师生共同探究的方法唤起学生的参与意识，完成作图方法和定义的学习，活跃了课堂气氛，锻炼了学生的合作能力．（三）例题精讲例1 如图，在△ABC 中，∠A =68°，点I 是内心．求∠BIC 的度数．CB AIF EDCBA师生活动：教师出示例题，学生思考、讨论，教师分析、引导：在△IBC 中，因为∠IBC ，∠ICB 分别是△ABC 中∠ABC 和∠ACB 的一半，从而由三角形的内角和定理，可由∠A 的度数求出∠BIC 的度数．师生共同完成解题过程．解：∵点I 是△ABC 的内心， ∴∠1=12∠ABC ，∠2=12∠ACB ．因而∠1+∠2=12(∠ABC +∠ACB )=12(180°-∠A )=12(180°-68°)=56°．∴∠BIC =180°-(∠1+∠2)=180°-56°=124°． 思考 你能用关于∠A 的代数式表示出∠BIC 吗？ 师生活动：教师出示思考问题，让学生完成． 答：∵∠IBC =12∠ABC ，∠ICB =12∠ACB ，∴∠IBC +∠ICB =12(∠ABC +∠ACB )=12(180°-∠A )∴∠BIC =180°-(∠IBC +∠ICB )=180°-12(180°-∠A )=90°+12∠A ．设计意图：实现知识的内化和升华，培养学生解决问题的能力．例2 △ABC 的内切圆⊙O 与BC ，CA ，AB 分别相切于点D ，E ，F ，且AB =9，BC =14，CA =13．求AF ，BD ，CE 的长．师生活动：学生思考并解决问题，教师选取几名学生的解答过程投影并订正． 解：设AF =x ，则AE =x ，CD =CE =AC -AE =13-x ，BD =BF =AB -AF =9-x ．OFEDCBA由BD +CD =BC ，得(9-x )+(13-x )=14． 解得x =4．因此AF =4，BD =5，CE =9．设计意图：让学生在应用知识的过程中，进一步加深对所学知识的认识与理解，培养学生的应用意识和能力．（四）挑战自我（1）已知△ABC 的三边长分别为a ，b ，c ，它的内切圆半径为r ．求△ABC 的面积． （2）已知Rt △ABC 的两条直角边AC ，BC 的长分别为b ，a ．求它的内切圆半径． 参考答案解：（1）如图所示，作△ABC 的内切圆，内心为点O ，E ，F ，G 为切点，连接OE ，OF ，OG ，OA ，OB ，OC ．设AB =c ，AC =b ，BC =a ，内切圆半径为r ．∵E 为切点， ∴OE ⊥BC ． ∴1122BOC S BC OE ar =⋅=△． 同理可得12AOB S cr =△，12AOC S br =△．∴1()2ABC AOB BOC AOC S S S S a b c r =++=++△△△△．（2）依题意作图，如下图所示，设Rt △ABC 的内切圆的半径为r ，AB =c ，⊙O 分别切AB ，BC ，AC 于点D ，E ，F ，连接OD ，OE ，OF ，则四边形OECF 是正方形，∴CE =CF =r ．B∴AF =AD =b -r ，BE =BD =a -r ． ∵AD +BD =AB ， ∴b -r +a -r =c ．∴r =2a b c+-． 又∵c∴r．设计意图：通过本环节让教师查看学生对刚刚学过的知识的掌握情况． （五）课堂练习1．在△ABC 中，∠A =40°，∠B =70°，点I 是△ABC 的内心．求∠AIB ，∠BIC 和∠AIC 的度数．2．已知⊙O 是△ABC 的内切圆，切点为D ，E ，F ，如果AE =2，CD =1，BF =3，且△ABC 的面积为6．求内切圆O 的半径r ．师生活动：教师找几名学生板演，讲解出现的问题． 参考答案1．解：如下图所示．∵∠BAC =40°，∠AB C=70°， ∴∠ACB =180°-40°-70°=70°．FB由例1得出的公式可得∠AIB=90°+12∠ACB，∠BIC=90°+12∠BAC，∠AIC=90°+12∠ABC．∴∠AIB=90°+12×70°=125°，∠BIC=90°+12×40°=110°，∠AIC=90°+12×70°=125°．2．解：连接AO，BO，CO．∵⊙O是△ABC的内切圆，且D，E，F是切点，∴AF=AE=2，BD=BF=3，CE=CD=1．∴AB=5，BC=4，AC=3．又S△ABC=6，∴1(453)62r++=．∴r=1．所以所求的内切圆O的半径为1．设计意图：通过本环节的学习，让学生巩固所学知识．（六）课堂小结这节课我们主要学习了：1．三角形的内切圆及其相关概念与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．注意：三角形的内心是三角形的三条角平分线的交点，它到三角形各边的距离相等．任何一个三角形都有且只有一个内心，三角形的内心在三角形的内部．2．三角形内切圆的作法．任选三角形的两个内角，分别作这两个内角的角平分线，以这两个内角平分线的交点为圆心，以该点到任意一条边的距离为半径画圆，该圆就是三角形的内切圆．师生活动：教师引导学生归纳总结本节课所学内容．设计意图：通过总结使学生梳理本节课所学内容，掌握本节课的核心内容．四、课堂检测设计1．△ABC的内切圆与三边的切点构成△EDF，则△EDF一定为（）．A．锐角三角形B．直角三角形C．钝角三角形D．等边三角形2．等边三角形的内切圆的半径、外接圆的半径和高的比为（）．A．1B．1∶2C．1 2 D．1∶2∶33．三角形的内心是三角形_____________的交点．4．在△ABC中，∠A=60°，∠B=80°，O是△ABC的内心，则∠AOB=________．5．如下图，⊙O是△ABC的内切圆，切点分别为D、E、F，∠B=60°，∠C=70°．求∠EDF 的度数．参考答案1．A．2．D．3．三条内角平分线．4．110°．5．解：如图，连接OE、OF．在△ABC中，∠A=180°-(∠B+∠C)=180°-(60°+70°)=50°．∵⊙O是△ABC的内切圆，∴AB⊥OF，AC⊥OE（圆的切线垂直于经过切点的半径）．在四边形AFOE中，∠EOF=360°-(∠A+∠AFO+∠AEO)=360°-(50°+90°+90°)=130°，∴∠EDF=12∠EOF=65°．。

三角形的内切圆学习目标:1、了解三角形内切圆的相关概念2、会画任意三角形内切圆,并会写作法 ３、掌握三角形内心的性质及简单应用 学习重点:内心的性质及简单应用 学习难点:内心的性质及简单应用 学习过程： 一、温故知新1、如右图:如果⊙O 经过△ABC 的三个顶点,则⊙O 叫做△ABC 的 ，圆心O 叫做△AB Ｃ的，反过来,△ＡBC叫做⊙O 的 。

△ABC 的外心就是A Ｃ、B Ｃ、AB 边的 交点。

2、三角形的三边的 交于一点，三角形的三个内角的 交于一点, 二、探究新知 (一)自主学习 1、内切圆 ①内切圆相关概念如图2，与三角形各边都 的圆叫做三角形的 ,三角形的内切圆的圆心叫做三角形的 ．这个三角形叫做圆的 ．三角形的内心就是三角形三条内角 的交点． 即：如图2,如果⊙Ｉ与△ABC 的三边 ,则⊙I 叫做△ABC 的 ,圆心I 叫做△ABC 的 ,反过来，△ＡBC 叫做⊙I 的 ．△ABC 的内心就是△ＡBC 的三个的交点。

②内切圆的作法已知△ABC ，画它的内切圆⊙O 作法：图2ﻬ1、分别作∠A,∠B 的 ,两平分线交于点Ｏ2、过点O 作AB 的垂线段,交AB 于D3、以点 为圆心，以 的长为半径，画圆 那么,所画的⊙O 就是△ABC 的（二)合作探究:1、三角形的内心与外心有什么区别?2、在三角形ABC 中,∠A ＝６８°，点Ｉ是内心,求∠ＢIC 的度数．(三）达标训练１、如图，⊙Ｏ是△ABC 的内切圆,与ＡB 、BC 、C Ａ分别切于点D 、E 、Ｆ， ∠D ＯE =1２０°，∠ＥOF =15０°，求∠A ＝ ,∠B ＝ ，∠Ｃ=2、如图为一张三角形铁皮,如何在它上面截一个面积最大的圆形铁皮?ﻫ(要求:写出作法)解:这个圆其实就是 作法：1、ﻬ2、B CC(第1题)3、３、△ABＣ的内切圆⊙Ｏ与AC、AＢ、BＣ分别相切于点Ｄ、E、F，且ＡB＝5厘米,BC=9厘米,ＡC=6厘米,求ＡＥ、BＦ和CD的长。

《三角形的内切圆》作业设计方案（第一课时）一、作业目标本作业旨在巩固学生对三角形的内切圆概念的理解，掌握内切圆的基本性质，以及能正确应用内切圆进行相关的计算和问题解决。

通过本作业的完成，提高学生的空间想象能力和逻辑推理能力。

二、作业内容（一）基础练习1. 掌握内切圆的定义及性质，能正确画出三角形的内切圆。

2. 理解内切圆半径与三角形边长的关系，能通过已知条件计算内切圆半径。

3. 掌握内切圆与三角形各边的关系，如内角平分线与对应边的关系等。

（二）进阶应用1. 通过具体实例，运用内切圆解决与三角形面积、周长等相关的实际问题。

2. 探索三角形内切圆与外接圆的关系，理解它们的异同点。

3. 理解并掌握利用内切圆解决几何问题的基本思路和方法。

（三）综合实践1. 完成一份关于三角形的内切圆的综合练习题，包括选择题、填空题和解答题等。

2. 小组合作，共同探讨三角形的内切圆在实际生活中的应用，并形成书面报告。

三、作业要求1. 独立完成：要求学生独立完成作业，不得抄袭他人答案。

2. 规范书写：要求学生书写规范，步骤清晰，逻辑严谨。

3. 及时反馈：要求学生按时完成作业，并做好错题记录，及时反馈学习中的疑问和困惑。

4. 注重过程：在解题过程中，要体现出对概念的理解和对方法的掌握，而不仅仅是答案的正确性。

5. 小组讨论：对于综合实践部分，要求学生积极参与小组讨论，充分发表自己的观点和看法，并做好记录和总结。

四、作业评价1. 评价标准：以准确性、规范性、完整性、创新性等方面为评价标准，全面评价学生的作业完成情况。

2. 互评与自评：鼓励学生进行互评和自评，互相学习和借鉴，提高解决问题的能力。

3. 教师点评：教师根据学生的作业完成情况，进行针对性的点评和指导，帮助学生查漏补缺，提高学习效果。

五、作业反馈1. 对于学生在作业中出现的共性问题，教师将在课堂上进行集中讲解和指导。

2. 对于个别学生的问题，教师将通过个别辅导的方式，帮助学生解决问题，提高学习效果。