第三章-目标规划
- 格式:doc
- 大小:149.50 KB
- 文档页数:9
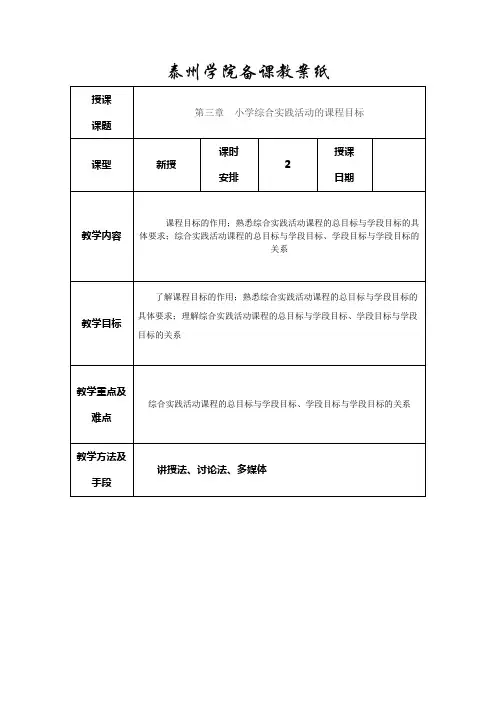

第三章课程目标与课程内容教学目标:理解课程目标的内涵、取向及其确定的依据;掌握课程内容的取向及其选择与组织原则;了解当代小学教育课程的目标与课程内容。
在整个教育系统中,确定课程目标,具有举足轻重的意义。
课程目标有助于指明课程编制工作的方向,有助于课程内容的选择与组织,并可作为课程实施的依据和课程评价的准则。
只有解决了课程目标是什么或为什么要教的问题,才能解决应该教什么的问题即课程内容问题。
因此,怎样确定课程目标,怎样选择课程内容,这是课程论和课程改革的基本问题。
一.课程目标(一)涵义课程目标是指那些人们需要掌握和形成的能力、态度、习惯、鉴赏和知识的形式(博比特)。
课程目标是根据教育宗旨和教育规律而提出的课程的具体价值和任务指标。
课程目标是对教育方针和教育目的的反映。
每一门课程既具有一般性的总体目标,又具有具体化的学段目标。
相关概念:教育宗旨、教育方针、教育目的、教育目标、教学目标宗旨、目的、目标具有内在的联系,从宗旨到目的再到目标是一个从宏观到中观再到微观的过程,越来越具体。
在教育系统中,教育宗旨、教育目的、教育目标、课程目标、教学目标等构成一个有机整体。
宗旨是指最终的价值追求,具有较强的理想色彩,一般体现为宏观的理念。
教育宗旨常以教育方针的形式贯彻、落实。
教育方针是国家根据政治、经济、文化发展的要求,为实现教育目的所规定的教育工作总方向,是教育政策的总概括,内容包括教育指导思想、培养人才的规格及实现教育目的的基本途径。
不同时期对教育方针的表述不同。
我国现阶段的教育方针:党的十七大报告指出,要“坚持育人为本、德育为先,实施素质教育,提高教育现代化水平,培养德智体美全面发展的社会主义建设者和接班人,办好人民满意的教育。
在教育理论界,教育宗旨往往表现为对教育目的的研究。
教育目的是教育活动的总目标,是社会对教育所培养的人才的总要求,它规定了人的质量规格和基本素质。
教育目的是教育实践活动的出发点。
教育目的受制于社会制度、民族文化传统与教育思想。


学习计划的目录应该怎么写第一章:学习目标与规划
- 学习目标的制定
- 学习计划的规划
- 时间管理技巧
第二章:学习方法与技巧
- 高效学习方法
- 记忆技巧与方法
- 阅读理解技巧
- 写作技巧与方法
第三章:学习动力与心态
- 提升学习动力
- 克服学习困难
- 保持学习心态
第四章:学习资源的获取与利用
- 网络学习资源的获取
- 图书馆学习资源的利用
- 社交学习资源的获取与利用
第五章:学习科目的策略
- 语文学习策略
- 数学学习策略
- 外语学习策略
- 科学学习策略
- 社会学习策略
第六章:学习效果的评价
- 学习成果的评价与分析
- 学习进程的监控
- 学习效果的改进与提高
第七章:学习整理与总结- 学习笔记的整理与总结
- 学习成果的总结
- 经验与教训的总结
第八章:学习技能的提高- 学习方法的提高
- 学习能力的提高
- 学习思维的拓展
第九章:学习社交与合作- 学习合作的方式和方法
- 学习社交的技巧
- 学习团队的建立与发展
第十章:学习生活的规划- 学习生活的平衡
- 学习生活的习惯
- 学习生活的享受
第十一章:学习未来的规划- 学业生涯的规划
- 职业生涯的规划
- 个人发展的规划
结语
以上为学习计划目录的初步规划,具体内容可根据实际情况进行调整和补充。
希望能够帮助大家更好地制定学习计划,提高学习效率,取得更好的学习成绩。

第三章课程与教学的目标和内容第一节。
课程与教学的目标第二节。
课程与教学的内容第一节课程与教学的目标一。
课程与教学目标概述(一)课程与教学目标的涵义课程与教学目标是指在课程与教学的设计(课程),实施和开发过程(教学)中所体现的教育价值的基本要求。
课程与教学目标是教育目的和培养目标的具体化(教育怎样的人,培养怎样的人)-------------也就是教育目的的表现形式就是上的课的目的1.课程目标(1)涵义:课程目标是指在课程设计与开发过程中(设计书本),课程本身要实现的具体要求。
---------------都是要求但是与课程与教学目标有什么不同(2)特征:课程目标具有整体性,连续性,层次性和积累性等特点。
--------整体性是指不可分割的,连续性也是,层次性指课程目标是指课程目标有大有小的,有总体的,有具体的,积累性是指目标是积累下来的。
(3)表述方式不同价值取向的课程目标有不同的表征方式。
泰勒等人主张“行为目标”的表述方式,认为课程目标是学习者预定发生的变化。
?斯坦豪斯则主张用“过程目标”或“内容目标”,即将课程目标表述为预先规定的学习内容,活动情境和过程。
-------------------------都是预定的,计划好的内容,活动情境,过程变化。
由于对课程目标的价值取向不同,所以,在制定课程目标时,其具体要求也不一样。
因此,当代各级各类课程目标的价值取向呈现多元化的趋势。
----------价值取向不同,制定的课程的目标也是不同的。
(4)课程目标的分类一门课程目标总是有一般性的总体目标和阶段性的目标组成的。
以新课程《语文》为例。
《语文课程标准》主要从总目标与阶段目标两个方面给了具体说明。
总目标共提出了10项要求,分别是:①在语文学习过程中,培养爱国主义感情,社会主义道德品质,逐步形成积极的人生态度和正确的价值观,提高文化品位和审美情趣。
②认识中华文化的丰厚博大,吸收民族文化智慧。
关心当代文化生活,尊重多样文化,吸取人类优秀文化的营养。



部门规划范文(最新)第一章:引言随着企业发展的不断壮大,各个部门的功能和职责也越来越明确。
为了更好地实现企业的战略目标,本部门制定了本部门规划,以确保目标的实现和持续增长。
第二章:部门概况2.1部门背景本部门隶属于企业的中枢部门,主要负责企业的市场拓展和销售业务。
2.2部门使命本部门的使命是通过市场拓展和销售业务,为企业创造价值,提升企业的品牌形象和市场地位。
2.3部门愿景本部门的愿景是成为市场拓展和销售领域的领先者,为企业持续增长提供强有力的支持。
2.4部门核心价值观本部门的核心价值观是团队合作、客户导向、创新求变、诚信可靠。
第三章:目标规划3.1长期目标通过市场拓展和销售业务,实现年度销售额的持续增长。
3.2中期目标建立强大的市场拓展团队,实现市场份额的增加。
3.3短期目标制定具体的销售计划,实现销售额的稳定增长。
第四章:策略规划4.1市场拓展策略通过分析市场需求,确定目标市场和客户群体,制定相应的市场拓展策略,打开新的销售渠道。
4.2销售策略建立高效的销售团队,制定具体的销售计划和销售目标,提升销售技巧和服务质量。
4.3客户关系管理策略建立完善的客户关系管理系统,加强对客户的维护和服务,提高客户满意度和忠诚度。
第五章:实施计划5.1组织结构调整根据部门的发展需求,合理安排部门的组织结构和人员配置,建立高效的团队。
5.2培训计划制定培训计划,提升团队成员的专业知识和业务技能,提高团队的整体素质。
5.3绩效考核制度建立科学、公正的绩效考核制度,激发员工的工作积极性和创造力,推动团队目标的实现。
5.4信息化建设通过引入先进的信息化系统,提高部门的工作效率和管理水平,实现数据的快速统计和分析。
第六章:风险控制6.1市场风险及时关注市场变化,预测市场趋势,制定应对策略,降低市场风险对部门发展的影响。
6.2销售风险建立合理的销售目标和销售预测机制,加强对销售过程的监控和管理,减少销售风险的发生。
6.3客户风险认真进行客户调研,了解客户需求和意见,及时回应客户反馈,提高客户满意度,减少客户风险的发生。

第三章 职业目标定位及其分解组合1.职业目标的确定综合第一部分(自我分析)及第二部分(职业生涯条件分析)的主要内容得出本人职业定位的SWOT 分析:结论:职业目标——将来从事(IT 行业的) 程序员职业职业发展策略——进入国营类型的组织(回到山东济南地区发展)职业发展路径——走管理路线2.职业目标的分解与组合把职业目标分成三个规划期,即:近期规划、中期规划和远期规划,并对各个规划期及其要实现的目标进行分解。
职业生涯规划总表计划名称时间跨度总目标分目标计划内容策略和措施备注短期计划(大学计划)2015年—2019年大学毕业时要达到英语六级水平,专业课要达到教学要求。
如果有精力可以考虑其他技能的大一要达到英语四级;大二要达到英语六级或在专业课方面要达到优秀。
计算机等级考试通专业学习、职业技能培养、职业素质提升、职业实践计划等大一以适应大学生活为主;大二以专业学习和掌握职业技能为主以及在人际关系的处理能力上有一个新的跨越;大三已经对大学生活有了一个更为准确的体会和大学生职业规划的重点优势因素(S)弱势因素(W)内部环境因素性格坚定,柔韧,遇到困难能够直面面对对于新环境的适应能力较差,不能很快地融入其中 机会因素(O)威胁因素(T)外部环境因素 一直生活在顺境中,享受着很好生活条件和教育条件, 社会大环境和谐社会就业形势复杂,人际关系复杂多变 分析在顺畅的社会环境,有更多好机遇,施展自己的才能 社会斗争现实残酷,性格上的适应力,使得今后踏入社会面临的挑战也便增多学习。
过认识,应更加注重专业技能的培养,特别是实际操作能力的培养;大四,更多面临的挑战是如何从大学生变为一个社会人。
积极地进行实践,锻炼自己的适应能力,为将来踏入社会积累经验中期计划(毕业后五年的计划)2019年—2024年计划毕业后第五年时要达到中阶层管理人员职位毕业后第一二年积累工作经验,从基层人员做起;第三年争取晋升机会,做团队的小组长等;第四五年随着工作经验的丰富,考虑向更有挑战岗位晋升,做到中高阶管理人员职场适应、三脉积累(知脉、人脉、金脉)、岗位转换及升迁等脱离大学,难免有不适应的过程。


《运筹学》教案-目标规划数学模型第一章:目标规划概述1.1 目标规划的定义与意义1.2 目标规划与其他规划方法的区别1.3 目标规划的应用领域1.4 目标规划的发展历程第二章:目标规划的基本原理2.1 目标规划的基本假设2.2 目标规划的数学模型2.3 目标规划的求解方法2.4 目标规划的评估与决策第三章:目标规划的数学模型3.1 单一目标规划模型3.2 多目标规划模型3.3 带约束的目标规划模型3.4 动态目标规划模型第四章:目标规划的求解方法4.1 线性规划求解方法4.2 非线性规划求解方法4.3 整数规划求解方法4.4 遗传算法求解方法第五章:目标规划的应用案例5.1 生产计划目标规划案例5.2 人力资源规划目标规划案例5.3 投资组合目标规划案例5.4 物流配送目标规划案例第六章:目标规划的高级应用6.1 目标规划在供应链管理中的应用6.2 目标规划在项目管理中的应用6.3 目标规划在金融管理中的应用6.4 目标规划在能源管理中的应用第七章:目标规划的软件工具7.1 目标规划软件工具的介绍7.2 常用目标规划软件工具的操作与应用7.3 目标规划软件工具的选择与评估7.4 目标规划软件工具的发展趋势第八章:目标规划在实际问题中的应用8.1 目标规划在制造业中的应用案例8.2 目标规划在服务业中的应用案例8.3 目标规划在政府决策中的应用案例8.4 目标规划在其他领域的应用案例第九章:目标规划的局限性与挑战9.1 目标规划的局限性分析9.2 目标规划在实际应用中遇到的问题9.3 目标规划的发展趋势与展望9.4 目标规划的未来研究方向10.1 目标规划的意义与价值10.2 目标规划在国内外的发展现状10.3 目标规划在未来的发展方向10.4 对运筹学领域的发展展望重点和难点解析重点环节一:目标规划的数学模型补充和说明:在讲解目标规划的数学模型时,重点关注单一目标规划模型和多目标规划模型的构建。
十四五规划和2035目标中能源电力内容2021年3月13日凌晨2点31分,新华社公开了正式版的《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要》。
第一篇开启全面建设社会主义现代化国家新征程第三章主要目标第二节“十四五”时期经济社会发展主要目标——生态文明建设实现新进步。
国土空间开发保护格局得到优化,生产生活方式绿色转型成效显著,能源资源配置更加合理、利用效率大幅提高,单位国内生产总值能源消耗和二氧化碳排放分别降低13.5%、18%,主要污染物排放总量持续减少,森林覆盖率提高到24.1%,生态环境持续改善,生态安全屏障更加牢固,城乡人居环境明显改善。
第三篇加快发展现代产业体系巩固壮大实体经济根基第八章深入实施制造强国战略第二节提升产业链供应链现代化水平立足产业规模优势、配套优势和部分领域先发优势,巩固提升高铁、电力装备、新能源、船舶等领域全产业链竞争力,从符合未来产业变革方向的整机产品入手打造战略性全局性产业链。
第三节推动制造业优化升级培育先进制造业集群,推动集成电路、航空航天、船舶与海洋工程装备、机器人、先进轨道交通装备、先进电力装备、工程机械、高端数控机床、医药及医疗设备等产业创新发展。
第四节实施制造业降本减负行动允许制造业企业全部参与电力市场化交易,规范和降低港口航运、公路铁路运输等物流收费,全面清理规范涉企收费。
第九章发展壮大战略性新兴产业着眼于抢占未来产业发展先机,培育先导性和支柱性产业,推动战略性新兴产业融合化、集群化、生态化发展,战略性新兴产业增加值占GDP比重超过17%。
第一节构筑产业体系新支柱聚焦新一代信息技术、生物技术、新能源、新材料、高端装备、新能源汽车、绿色环保以及航空航天、海洋装备等战略性新兴产业,加快关键核心技术创新应用,增强要素保障能力,培育壮大产业发展新动能。
推动生物技术和信息技术融合创新,加快发展生物医药、生物育种、生物材料、生物能源等产业,做大做强生物经济。
-------学业规划姓名:吴广贵 系别: 电子工程系专业班级: 11级电子信息2班 学号:201130140202DongGuang Vocational & Technical College目录第一章引言1.1 引言第二章自我分析2.1个人情况2.2自我盘点2.3自我总结第三章学业规划3.1专业现状分析3.2学习情况分析3.3课余生活安排计划第四章结束语第一章1.1 引言规划学业,追求卓越当你的眼神开始回到书本,全神贯注地投入学习时候,似乎带着高中的惯性,你像是上了发条般机械的侵吞一切遇到的知识。
埋头书海,无暇四顾。
当你日日奔波在寝室,课堂与图书馆时候,你或许暗自庆幸,享受着这种忙碌而又充实的时光。
然而,当你抬头向前方探寻,却是茫然一片,云里雾里。
难道就要这样放弃对梦想的追逐,放弃对成功的追求,放弃自己兀自存留的对精彩的希冀?我知道你在害怕生命就这样苍白地逝去,我知道你不甘青春在日复一日的绝望中流逝,我知道你在嘈杂的课堂上被喧嚣叩击着心灵,痛苦万分,却难以自拔。
你回望曾经,那时的你可以肆无忌惮的叫嚣十年之后成为千万富翁,那时的你可以对着全班同学的面决心改革中国教育现状,那时的那时,一切只因为那时。
只因为那时的年少轻狂,只因为那时的少不更事。
而现在,当你真的要准备去实现当年的豪言壮语时,却不得不蜷缩在现实的角落,弱弱地呼吸,探出手来想要拿起就在手边却布满灰尘的纸片,上面写着:信仰。
你不该丢弃信仰,你应该对自己负责,人生这本书今天翻到了大学这一页,如何装点,如何规划,是你我必须面对的问题,现在我选择做一份自己的学业规划,期待它成为我未来学习生活的罗盘针、导向标。
第二章自我分析2.1 个人情况我出生于广西一个偏远的山区,去年八月份被东莞职业技术学院录取。
我喜欢写字,喜欢与人交谈,身体心理状况都很好,是一个非常有活力并且乐观向上的一个大学生。
2.2 自我盘点内因是事物发展的根本原因。
对自己有一个正确客观全面的评价是追求卓越的必要条件,清醒的认识自己的优缺点,明白自己的长处和不足,才能在大学生活中有所提升,有所斩获。
管理实训:第三章分析一份计划书下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!第一节:引言在管理实训课程中,学生们常常需要分析并评价一份计划书。
第三章 目标规划 第一节 目标规划的数学模型目标规划法是求一组变量的值,在一组资源约束和目标约束条件下,实现管理目标与实际目标之间的偏差最小的一种方法。
应用目标规划法解决多种目标决策问题时,首先要建立目标规划模型。
目标规划模型由变量、约束和目标函数组成。
为具体说明目标规划与线性规划在处理问题方法上的区别,先通过例子介绍目标规划的有关概念及数学模型。
一、举例例 1 某厂生产Ⅰ、Ⅱ两种产品,已知计划期有关数据如下,求获利最大的生产方案。
生产有关数据表ⅠⅡ 拥有量 原材料 (公斤) 2 1 11 设备台时(小时) 利润 (元/件) 1 82 1010用线性规划方法求解:设Ⅰ、Ⅱ两种产品产量分别为x 1,x 2⎪⎩⎪⎨⎧≥≤+≤++=0,102112108max 21212121x x x x x x x x z可得 Z=62元,X=(4,3)T但实际决策时,有可能考虑市场等其它方面因素,例如按重要性排序的下列目标:据市场信息,产品Ⅰ销售量下降,要求产品Ⅰ产量低于产品Ⅱ产量; 尽可能充分利用现有设备,但不希望加班; 达到并超过计划利润指标56元。
这样考虑生产计划问题即为多目标规划问题。
下面结合上述例题介绍有关建立目标规划数学模型的基本概念。
二、目标规划基本概念1. 设x 1,x 2为决策变量,并引入正、负偏差变量d +、d —正偏差变量d +表示决策值超过目标值的部分;负偏差变量d —表示决策值未达到目标值的部分,d +,d -≥0。
决策值不可能既超过又未达到目标值,因此恒有d +×d -=0。
2.绝对约束和目标约束绝对约束指必须严格满足的“≤,≥,=” 约束,称为硬约束,例如线性规划中的约束,不满足它们的约束称为非可行解;目标约束是目标规划所特有的,它把约束的右端常数项看作追求的目标值,允许出现正、负偏差,用“d +、d -”表示,称为软约束。
约束的一般形式为:i i i j iij g d d X C =-++-∑式中i g ——第i 个目标约束的目标值;ij C ——目标约束中决策变量的参数;+-i i d d 、——以目标值i g 为标准而设置的偏差变量。
线性规划问题的目标函数,在给定目标值和加入正、负偏差变量后可变为目标约束;同样,线性规划问题的绝对约束,加入正、负偏差变量后也可变为目标约束。
例如,例1中线性规划问题的目标函数:Z = 8 x 1 + 10x 2 ,可变换为目标规划问题中的目标约束:8 x 1 + 10x 2 =56 + d +-d - ;而同样,线性规划问题的绝对约束:2x 1 + x 2 ≤11,可变换为目标规划问题中的目标约束:2x 1 + x 2 = 11-d - 。
建立约束需注意的问题时:(1)对于绝对约束,i g 则为资源限制值,上式中不加+-i i d d 、。
(2)非负约束是指偏差变量非负,0≥+-i i d d 、,至于决策变量是否要求非负,依具体问题要求决定。
(3)在目标规划约束中,凡已列入目标约束的资源约束,不应再列入资源约束。
(4)如果有明显的目标要求,可在+-i i d d 和中只选一个。
3.优先级与权系数要解决的规划问题往往有多个目标,而决策者对于要达到的目标是有主次之分的。
要求首先达到的目标赋予优先级P 1,稍次者赋予P 2 ,…。
这里规定:不同级目标重要性差异悬殊,P k >> P k+1,即先保证上一级目标实现的基础上再考虑下一级目标,低级目标的多大收获也不能弥补高级目标的微小损失。
若要区别具有相同优先级的目标的差别,可赋予不同的权系数w j 。
4.目标函数目标规划问题的目标函数是由各目标约束不同的正、负偏差变量d +、d -,优先级P k 与权系数w j 所构成的。
与线性规划不同的是目标函数中不含决策变量x j 。
当各目标值确定之后,决策者希望的是尽可能缩小对目标值的偏离。
因此,目标规划问题的目标函数只能是:Min Z = f (d +,d -)。
其基本形式有下列三种:要求恰好达到目标值,即正、负偏差变量都应尽可能的小,这时目标函数的形式:min Z = f (d + + d -)要求不超过目标值,即正偏差变量应尽可能的小,这时目标函数的形式: min Z = f (d + )要求超过目标值,即负偏差变量应尽可能的小,这时目标函数的形式: min Z = f ( d -)由此可见,目标规划比线性规划体现了新的灵活思想,约束和目标都不看作是绝对的。
决策者根据要求赋予各目标不同的优先级、权系数,构造目标函数。
下面举例说明。
例2 某构件公司商品混凝土车间生产能力为20t/h ,每天工作8h ,现有2个施工现场分别需要商品混凝土A 为150t ,商品混凝土B 为100t ,两种混凝土的构成、单位利润及企业所拥有的原材料见下表所示,现管理部门提出:原材料消耗、拥有量R 单位利润表(1)充分利用生产能力; (2)加班不超过2h ;(3)产量尽量满足两工地需求; (4)力争实现利润2万元/天试建立目标规划模型拟定一个满意的生产计划。
解: 1.确定变量设21x x 、分别为两种混凝土的产量。
2.约束条件 (1)目标约束:1P 级:要求生产能力充分利用,即要求剩余工时越小越好。
1601121=-+++-d d x x 其中要求01→-d2P 级:要求可以加班,但每日不超过2h ,即日产量不超过200t 。
2002221=-+++-d d x x 其中要求02→+d3P 级:两个工地需求尽量满足,但不能超过需求。
15031=+-d x 其中要求03→-d10042=+-d x 其中要求04→-d因需求量不能超过其需求,故++43d d ,=04P 级:目标利润超过2万元。
20000801005521=-+++-d d x x 其中要求05→-d(2)资源约束水泥需求不超过现有资源:5025.035.021≤++x x砂需求不超过现有资源:1306.055.021≤++x x(3)非负约束)521(00021,,,、,, =≥≥≥+-i d d x x i i3.目标函数依目标约束中的要求,第三层目标中有两个子目标,其权数可依其利润多少的比例确定,即100:80,故W 1=5,W 2=4。
故目标函数为---+++++=544332211min )45(d P d d P d P d P Z整理得该问题的目标规划模型为:目标:---+++++=544332211min )45(d P d d P d P d P Z 约束条件:1601121=-+++-d d x x 2002221=-+++-d d x x15031=+-d x10042=+-d x20000801005521=-+++-d d x x5025.035.021≤++x x 1306.055.021≤++x x)521(00021,,,、,, =≥≥≥+-i d d x x i i例 3 例1的决策者在原材料供应受严格限制的基础上考虑:产品Ⅰ产量低于产品Ⅱ产量;其次,尽可能充分利用现有设备,但不希望加班;再次,达到并超过计划利润指标56元,求决策方案。
解 按决策者的要求,分别赋予三个目标不同的优先级P 1,P 2,P 3。
然后建立目标规划模型如下:min z = P 1d 1+ + P 2(d 2++d 2-) + P 3d 3- 2x 1 + x 2 ≤ 11 x 1-x 2 + d 1-- d 1+ = 0 x 1 +2x 2 + d 2-- d 2+ = 10 8x 1 +10x 2 + d 3--d 3+ = 56x 1,x 2,d i -,d i + ≥ 0, i = 1,2,3目标规划数学模型的一般形式:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥==≥≤==-++=+-=+-=++=--=∑∑∑∑n j d d x m i b x a K k g d d x c d w d w p z k k j n j i j ij k k k n j j kj k lk Kk k lk Ll l ,,2,1,0,,,,2,1,),(,,1,)(min 1111建立目标规划数学模型时,需要确定目标值,优先级,权系数等,它们都具有一定的主观性,模糊性,通常采用专家评定法给予量化。
第二节 目标规划的图解法对于只有两个决策变量的目标规划数学模型,可采用图解法分析求解,这对于了解目标规划一般问题的解题思路也很有帮助。
下面用例2加以说明。
类似于线性规划,先在平面直角坐标系第一象限绘出各约束条件。
绝对约束的作图与线性规划相同,对于目标约束,先绘出d i +,d i -= 0对应的直线,然后在直线旁相应侧标注d i +,d i -,如图3-1所示。
根据目标函数中的优先级对下图进行分析,即可找到满意解(由于目标规划问题常出现非可行解,因此称目标规划问题的最优解为满意解)。
图3-1例2的目标规划的图解由图可见,首先考虑绝对约束:2x 1 + x 2 ≤11,解的可行域为三角形 0AB ,然后按优先级P 1,目标函数中要求min d 1+,解域缩减至0BC 内;再按优先级P 2,目标函数中要求min (d 2++d 2-),解域缩减至线段ED 上;最后按优先级P 3,目标函数中要求min d 3-,因此最终满意解域为线段GD 。
可求得相应坐标:G (2,4),D (10/3,10/3)。
GD 的凸线性组合都是该目标规 划的解。
目标规划问题求解时,把绝对约束作为最高优先级(但不必赋P 1)例中能依次满足d 1+=0,d 2++d 2-=0 d 3-=0,因此z *=0。
但大多数情况下并非如此,还可能出现矛盾,这可以通过下面的例子加以说明。
FE例3某电子设备厂装配A、B两种型号同类产品,每装配一台需占用装配线1小时。
每周装配线开动40小时,预计每周销售:A产品24台,每台可获利80元;B产品30台,每台可获利40元。
该厂确定的目标为:第一目标:充分利用装配线每周开动40小时;第二目标:允许装配线加班,但加班时间每周不超过10小时;第三目标:装配数量尽量满足市场需求。
要求建立上述问题的数学模型并求解。
解设x1,x2分别为产品A、B的计划产量。
对于第三目标,由于每台A 产品利润是B产品的2倍,因此取其权系数分别为2,1。
建立目标规划模型:min z = P1d1-+ P2d2+ + P3(2d3-+d4-)x1 + x2 + d1--d1+ = 40x1+ x2 + d2--d2+ = 50x1 + d3--d3+ = 24x2 + d4--d4+ = 30x1,x2,d i-,d i+≥0,i = 1,2,3,4图3-2 例3的目标规划的图解由图3-2可见,在考虑了第一目标和第二目标之后,x1和x2的取值范围为ABCD。