河北科技大学2007—2008高数试卷A

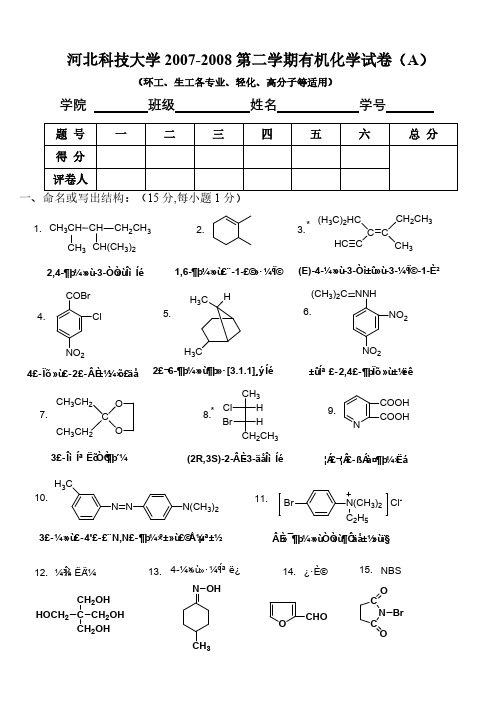
河北科技大学2007——2008学年第二学期《生物化学》期末考试试卷学院班级姓名学号一名词解释（每题3分，共18分）1．结构域：2．别构效应：3．增色效应：4．糖酵解途径：5．酮体：6．转氨基作用：二选择题（每题1分，共20分）1．下列寡糖中，不具有还原性的是 ( )A．蔗糖 B. 乳糖 C. 麦芽糖 D. 纤维二糖2．下列脂质中，属于不可皂化脂质的有( )A．磷脂 B.糖脂 C. 甘油磷脂 D. 萜3. 下列沉淀蛋白质的方法中，没有导致蛋白变性的方法是( )A．等电点沉淀 B.重金属盐沉淀法 C.生物碱和酸沉淀法 D. 加热变性沉淀法4. 参与酚试剂反应的氨基酸是( )A．Tyr Trp B. Met Trp C. Tyr Ser D. Ser Met5. 可以使得二硫键氧化断裂的试剂是( )A．尿素 B.巯基乙醇 C.二硫苏糖醇 D.过甲酸6. 下列分离蛋白质的方法中，( )不是根据蛋白电荷不同的性质进行分离的A．电泳 B.离子交换层析 C.亲和层析 D.聚丙烯酰胺凝胶电泳7. 有一混合蛋白质溶液，各种蛋白质的pI分别为4.6、5.0、5.3、6.7 ,电泳时欲使各种蛋白质都泳向正极，缓冲液的pH值应该是( )A．5.0 B. 4.0 C. 6.0 D. 7.08. 下列氨基酸中，( )含氮量最高A．Arg B. His C. Lys D.Pro9. 酶的竞争性抑制剂具有下列哪种动力学效应( )A．V max不变，Km增大 B. V max不变，K m减小C. V max增大，K m不变D. V max减小，K m不变10. 能与受体结合，形成激素－受体复合物，进入细胞核调节基因表达的激素是( ) A．甲状腺素 B.肾上腺素 C. 糖皮质激素 D.前列腺素11. 将RNA转移到硝酸纤维素膜上，进行分子杂交的技术叫( )A．Southern杂交法 B. Northern杂交法C. Eastern 杂交法D. Western 杂交法12. 最终经三羧酸循环彻底氧化为CO2和H2O和产生能量的物质有( )A．丙酮酸 B. 脂肪酸 C.β－羟丁酸 D.以上都是13．线粒体外脂肪酸合成的限速酶是( )A．酰基转移酶 B.乙酰CoA羧化酶C. 内毒碱脂酰CoA转移酶Ⅰ D．内毒碱脂酰CoA转移酶Ⅱ14. 人类嘌呤分解代谢的最终产物是( )A．尿酸 B.氨 C. 尿素 D.β－氨基异丁酸15. 核糖核苷酸还原为脱氧核糖核苷酸是在核苷二磷酸水平上完成的，而脱氧尿苷酸转化为脱氧胸苷酸是在( )完成的。

河北科技大学2017-2018学年《高等数学》（上册）期末考试A 卷一、 单项选择题（每小题3分，共15分）1. 若函数21,,()1,x x f x x ax b ≤⎧=⎨>+⎩在1x =处连续且可导，则【 】 A. 0,1a b == B. 2,1a b ==- C. 1,1a b =-= D. 3,2a b ==2. 曲线2y x =与直线1x =及0y =所围成的图形绕着y 轴旋转一周所形成的旋转体的体积为【 】 A. π2 B. π5 C. 3π2 D. 5π43. 当0x →时，sin e e x x -与n x 是同阶的无穷小量，则n 的值为【 】A. 1B. 2C. 3D. 44. 函数2ln(1)y x =+图形的凹区间是【 】A. []2,2-B. []1,4C. []1,1-D. []0,15. 方程510x x +-=【 】A. 只有一个正实根B. 无实根C. 有两个实根D. 有五个实根二、 填空题（每小题3分，共15分）1. 极限20lim ln x x x +→= . 2. 曲线1e y y x =+在点(0,1)处的切线的斜率k = .3. π42π2(cos sin )d x x x x --=⎰ .4. 若1ln cos y x=，则d y = . 5. 若()f x 的一个原函数是2ln x x ，则(e )d x f x =⎰ .三、 计算题（每小题7分，共21分）1. 设21,cos ,x t y t ⎧=+⎨=⎩，求π2d d t y x =与22d d y x . 2.求x ⎰.3.设21()d t f x t -=，求10x ⎰. 四、 解答题（每小题8分，共24分）1. 讨论函数11ln(1),10,()e ,0,1x x x f x x x -+-<<⎧⎪=⎨⎪≥≠⎩的连续性，若有间断点，指出其类型. 2. 求函数543121540y x x x =+-的极值.3. 求圆3cos r θ=与心形线1cos r θ=+所围的公共部分的面积.五、 解答题（每小题8分，共16分）1. 设()f x 在0x =的某邻域内有定义且(0)0f =，若20sin ()1lim 2e 1x x xf x →⋅=-，求(0)f '. 2. 已知函数()f x 在区间(,)-∞∞内可导，且lim ()e x f x →∞'=，又lim x x x c x c →∞+⎛⎫ ⎪-⎝⎭[]lim ()(1)x f x f x →∞=--，试利用拉格朗日中值定理求常数c 的值. 六、 证明题（9分） 设函数0()cos d xS x t t =⎰.（1）当n 为正整数，且π(1)πn x n ≤<+时，利用定积分的几何意义和性质证明2()2(1)n S x n ≤<+；（2）证明()2lim πx S x x →+∞=.。

河北科技大学2018-2019学年《高等数学》（上册）期末考试A 卷 一、单项选择题（每小题3分，共15分） 1. 11(cos 3)d =x x x x -+⎰【 】 A. 1 B. 0 C. 2- D. 22. 设函数()y f x =在点0x x =处有0()2f x '=，则当0x ∆→时，该函数在点0x x =处的微分d y 【 】A. 是与x ∆等价的无穷小B. 是与x ∆同阶的无穷小C. 是比x ∆低阶的无穷小D. 是比x ∆高阶的无穷小3. 当0x >时，总有()()()g x f x h x ≤≤，且lim ()lim ()2x x g x h x →+∞→+∞==，则lim ()x f x →+∞=【 】A.0B.1C.2D. 34. 曲线y =y x =所围成的图形的面积为【 】 A.112 B.16 C.14D. 2 5. 如果当0x >时，31()d 3xf x x x C =+⎰，则311d ()x f x =⎰【 】 A.ln 3 B.ln 2 C.1 D. 0二、 填空题（每小题3分，共15分）1. 极限22lim 1e xx a x a →∞⎛⎫+= ⎪-⎝⎭，则a = . 2. 过点(0,1)且切线斜率为23x 的曲线方程为 . 3. 设函数20cos d ()x t tF x x =⎰，则极限0lim ()x F x →= . 4. 函数3223y x x =-的极小值为 .5. 设sin 2y x =，则(6)()y x = .三、 计算题（每小题7分，共21分）1. 计算不定积分.2.已知函数sin,0,(),0,x xf xx x<⎧=⎨≥⎩求其导数()f x'.3.求由曲线2y x=，直线1x=，0y=所围成的图形分别绕着x轴及y轴旋转一周，计算所形成的两个旋转体的体积.四、解答题（每小题8分，共40分）1.讨论函数,11,()1,11x xf xx x-≤≤⎧=⎨<->⎩或的连续性，若有间断点，判别其类型.2.计算不定积分x x⎰.3.求曲线(y x=-.4.求曲线sin,cos2x ty t=⎧⎨=⎩在π4t=处的切线方程和法线方程.5.求定积分e1ln d x x x⎰的值.五、综合题（9分）设函数()f x在闭区间[0,2]上连续，在开区间(0,2)内可导，且(0)1f=，(1)(2)2f f+=，证明：在(0,2)内至少存在一点ξ，使得()0fξ'=.。

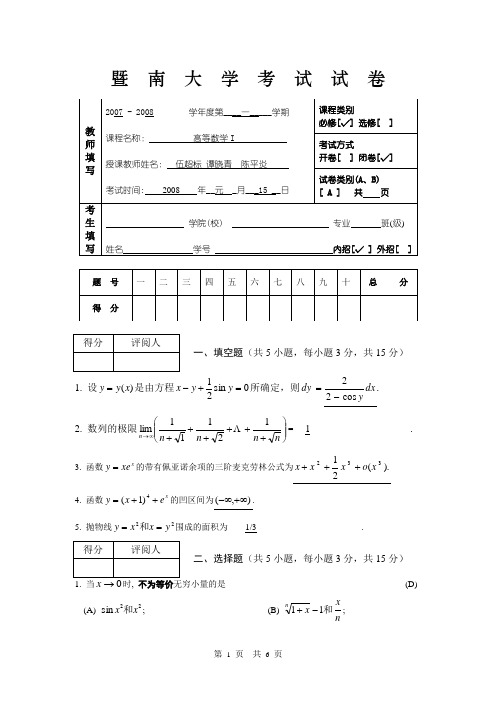
暨 南 大 学 考 试 试 卷一、填空题（共5小题，每小题3分，共15分）1. 设)(x y y =是由方程0sin 21=+-y y x 所确定，则=dy dx ycos 22-. 2. 数列的极限⎪⎪⎭⎫⎝⎛++++++∞→n n n n n 12111lim = __1____________________. 3. 函数xxe y =的带有佩亚诺余项的三阶麦克劳林公式为).(21332x o x x x +++4. 函数xe x y ++=4)1(的凹区间为),(+∞-∞.5. 抛物线22y x x y ==和围成的面积为____1/3________________________.二、选择题（共5小题，每小题3分，共15分）1. 当时, 不为等价无穷小量的是 (D) (A) 22sin x x 和; (B)nx x n和11-+;(C) x x 和)1ln(+; (D) 2cos 1x x 和-.2.设]1,0[上0)(">x f ,则)1()0()0()1(),1('),0('f f f f f f --或几个数的大小顺序为(B)(A) );0()1()0(')1('f f f f ->> (B) );0(')0()1()1('f f f f >-> (C) );0(')1(')0()1(•f f f f >>- (D) ).0(')1()0()1('f f f f >-> 3. 以下函数有可去间断点的是 (B )(A) ⎩⎨⎧>-≤-=;0,3,0,1)(x x x x x f (B) ;39)(2--=x x x f(C) ⎪⎩⎪⎨⎧=≠=;0,0,0,1sin )(x x xx f (D) .|sin |)(x x x f = 4. 摆线⎩⎨⎧-=-=)cos 1(),sin (θθθa y a x 的一摆)20(πθ≤≤的长度为 (D)(A) a 2; (B) a 4; (C) a 6; (D) a 8.5. 函数],[)(b a x f 在区间上连续是],[)(b a x f 在可积的 (A) (A) 充分条件; (B) 必要条件;(D) 即不是充分条件也不是必要条件.三、计算题（共7小题，每小题7分，共49分）1. 求定积分⎰210arcsin xdx ;解: 原式⎰--=21022101|arcsin dx xx x x ----------------------------------4⎰--+=21022)1(112112x d x π----------------------------------5 2102112x -+=π--------------------------------------------6.12312-+=π----------------------------------------------7 2. 求极限3sin 1tan 1limx xx x +-+→;解: 原式)sin 1tan 1()sin 1(tan 1lim3x x x x x x ++++-+=→-------------------------------------------------230sin tan lim21x xx x -=→ )21~cos 1,~sin ,0(cos )cos 1(sin lim 21230x x x x x xx x x x -→-=→时当 --------5.4121lim 21320=⋅=→x x x x -----------------------------------------------------------------73. 设)(x y y =由参数方程⎪⎩⎪⎨⎧==te y t e x ttsin ,cos 所确定，求22dx y d ; 解:)sin (cos t t e dt dx t -=, )cos (sin t t e dtdyt +=,-------------------------------------2,s in c o s c o s s in t t t t dtdx dt dy dx dy -+==-------------------------------------------------------4dx dtt t t t dt d dx dy dx d dx y d ⋅-+==)sin cos cos sin ()(22------------------------------------------------6 )sin (cos 1)sin (cos )cos (sin )cos (sin 222t t e t t t t t t t -⋅-++-=.)s i n (c o s 23t t e t -=--------------------------------------------------------------------74. 求不定积分⎰+x x xdxcos sin cos ;解: 原式⎰+-++=dx x x x x x x cos sin )sin (cos )sin (cos 21-------------- -- ----------------------3⎰⎰+++=x x x x d dx cos sin )cos (sin 2121----------------------------------------------------5C x x x +++=|cos sin |ln 2121.---------------------------------------------------75. 求极限2020222)1(limxdte t x x tx ⎰-→+;解: 原式22222)1(limxdt e t ex t x x ⎰+=-→------------- ---------------------------------------222022)1(limx dt e t x t x ⎰+=→-----------------------------------------------------------4xxe x x x 22)1(lim 440⋅+=→------------------------------------------------------------61)1(lim 440=+=→x x e x .-------------------------------------------------------------76. 求过点)0,23(与曲线21xy =相切的直线方程; 解: 设切点为)1,(20x x , 32'xy -=, 所以切线方程为-----------------------------1 )(21032x x x x y --=-.-----------------------4因)0,23(过切线, 所以)23(210032x x x --=-.-----------------------6 解得.10=x 因此切线方程为 .032=-+x y --------------------------------------7 7. 讨论瑕积分⎰10q x dx(q >0)的收敛性，如果收敛则计算其值.解: 对任意)1,0(∈ε,⎪⎪⎩⎪⎪⎨⎧≠--=-=-==--⎰.1),1(1111,1,ln |ln 11111q q x q q x x dx q q q εεεεε------------------------------------------3因此⎪⎩⎪⎨⎧≥∞+<-=⎰+→.1,,1,11lim10q q q x dx qεε--------------------------------------------------------------------6即1≥q 发散,当1<q 时收敛,其值为q-11.----------------------------------------------------------7四、应用题（共2小题，每小题8分，共16分）h m, 底面半径为r m , 桶内盛满了某种液体. 试问要把桶内的液体全部吸出需要作多少功? 已知这种液体的密度为ρ.解: 建立如图所示的坐标. 在任一小区间 上的一薄液体的 O的重力为dx r g 2ρπ(KN)----------------------------------3这薄层液体吸出桶外所做的功(功元素)为 xdx r g dW 2ρπ=----------------------------5所求的功为 hh x r g xdx r g W 02202|21ρπρπ==⎰2221h r g ρπ=(KN).---------------------8 2. 要做一个容积为V 的圆柱形罐头筒, 怎样设计才能使所用的材料最省? 解: 设底面半径为r , 则高为2r Vπ,表面积为 .0,2222222>+=⋅+=r r Vr rV r r S ππππ------------------------------------3令022'2=-=rV r S π得3πV r =,--------------------------------------------------------------------------5 又0|)42(|'333>+===πππV r Vr r V S , 因此当3πV r =时S 取最--------------------------------------7 即当底面半径为3πV,高为3πV时所用的材料最少.--------------------------------------------------8五、证明题（共1小题，每小题5分，共5分）1. 设)(x f 在区间],[b a 上连续,且0)(>x f ,⎰⎰∈+=x bx ab a x t f dtdt t f x F ],[,)()()(. 证明: (1) 2)('≥x F ; (2) 方程0)(=x F 在),(b a 内有且仅有一个根.证明: (1) .2)(1)(2)(1)()('=⋅≥+=x f x f x f x f x F ---------------------------------------------2 (2) )(x F 在],[b a 上连续, 且]d ,[x x x +0)()()()()()()(<-===⋅⎰⎰⎰⎰b a b a baa bdt t f t f dt •dt t f t f dt x F b F a F ,因此由介值定理)(x F 在),(b a 至少有一根, ----------------------------------------------------------4 又0)('>x F , 所以)(x F 在],[b a 上单调增, 因此)(x F 在),(b a 是只有一根.----------------5。

学院 专业 班级 学 姓名封线内不要答题 密封线内不要答题江 苏 科 技 大 学 07 － 08 学年（2）学期高等数学A2课程试题(A )卷一． 填空题(每小题4分，共20分)1．设),,(22xy e y x f z -=其中f 具有一阶连续偏导数,则____________________=∂∂xz2._____________________222=++⎰ds z y x L,其中3,sin ,cos :===z t y t x L)0(π≤≤t3.微分方程065=-'+''y y y 的通解_____________________=4.幂级数nn n xn n 11)1(21+--∑∞=-的收敛域为___________________________5.⎰=++-Lxxdy x e dx y ye_______________________________)()(33,其中L 是顺时针方向的圆周122=+y x二、单项选择题(每小题4分，共20分)1.曲面3=+-xy z e z 在点)0,1,2(P 处的法线方程是( ))(A 001122-=-=-z y x )(B 101122--=-=-z y x )(C02112-=-=-z y x )(D102112--=-=-z y x2.),(y x f x ',),(y x f y '在),(00y x 处存在是),(y x f 在该点的方向导数存在的( ))(A 充分条件)(B 必要条件 )(C 充要条件 )(D 无关条件3.设{}0,1),(22≥≤+=x y x y x D ,),(y x f 为D 上的连续函数,则dxdyy x f D)(22⎰⎰+为( ))(A rdr r f )(12⎰π⎰1)()(r d r r f B π ⎰1)(2)(r d r r f C π⎰12)(2)(r d r r f D π4.级数)cos1()1(1na n n --∑∞=(常数0>a )( ))(A 发散 )(B 条件收敛 )(C 绝对收敛 )(D 收敛性与a 的取值有关5.方程x e y y y x 2sin 52=+'-''的一个特解应具有的形式( )x Ae A x 2cos )()2s i n 2c o s ()(x B x A xe B x +)2sin 2cos ()(x B x A e C x+)2s i n 2c o s ()(2x B x A e x D x +三.解下列各题(3⨯6分=18分)1.计算dxdy x y x D)(22-+⎰⎰ 其中D 是由直线x y y ==,2及x y 2=所围成的闭区域2.判别级数nn n 5sin31π∑∞=的敛散性3．求微分方程sin =-+xx x y dxdy 满足初始条件1==πx y的特解四 .解下列各题(3⨯7分=21分) 1．设)11(11x y f x z -+=求证:222z yz yxz x =∂∂+∂∂2．计算dSy x z )342(⎰⎰∑++,其中∑为平面1432=++z y x 在第一卦限中的部分3．将积分dzz dy dx y x yx x⎰⎰⎰--+-2222222110化为球面坐标系下的积分并求其值五（本题共8分）计算⎰⎰∑++zdxdy ydzdx xdydz ,其中∑为半球面222yx R z --=的上侧六.(本题共7分) 将651)(2++=x x x f 展开成1+x 的幂级数七．(本题6分)设)(x f 与)(x g 在()+∞∞-,内可导,0)(≠x g ,且有)()(x g x f =', )()(x f x g =',)()(22x g x f ≠,试证明方程0)()(=x g x f 有且仅有一个实根07-08高等数学A2课程试题（A ）卷参考答案及评分标准一．填空题（每小题4分，共20分） 1．122xy xf yf e ''+ 2．2π3．612x x y c e c e -=+ 4．(1,1)- 5．32π-二．单项选择题（每小题4分，共20分） 1（C ） 2（D ） 3（A ） 4（C ） 5（B ）三.解下列各题（每小题6分，共18分） 1. 22()Dx y x dxdy +-⎰⎰解:222102()yydy x y x dx =+-⎰⎰3分=1366分2．解：1113sin5limlim3sin5n n n n n nnnu u ππ+++→∞→∞=2分=315< 5分因此原级数收敛 6分 3．解：1sin (),()x P x Q X xx==1分()()()P xdx Px dx y e Q x e dx c -⎡⎤⎰⎰=+⎢⎥⎣⎦⎰ 2分=11sin dx x x dx e dx c x x e⎰⎡⎤⎢⎥-+⎢⎥⎣⎦⎰⎰3分=1(cos )x c x-+ 4分 当,1x y ππ==时,c=-1 5分1(cos 1)y x xπ∴=-+-特解为6分三．解下列各题（每小题7分，共21分） 1.证明：令1111(,,)()F x y z f zx yx=--1分则221111()x F f xy x x ''=--2分22111111()()()y F f f yxyyx y'''=---=-3分21z F z'=-4分22111()x z F zz f x F x y x '⎡⎤∂'∴=-=--⎢⎥'∂⎣⎦ 5分2211()z z f yyyx∂'=-∂ 6分因此222z z x yz x y∂∂+=∂∂ 7分2..解:4423z x y =--42,3z z xy∂∂=-=-∂∂2分原式=44(42)233Dx y x y ⎡--++⎢⎣⎰⎰ 5分 (其中D 是0,0,123x y x y ==+=直线围攻成的区域)=43Ddxdy ⎰⎰= 7分3.解:001z y x ≤≤⎪Ω≤≤⎨⎪≤≤⎪⎩在球面坐标系下变为在球面坐标系下变为: 00402r πϕπθ⎧⎪≤≤⎪⎪≤≤⎨⎪⎪≤≤⎪⎩ 4分原式=42240cos sin d d drππθϕϕϕ⎰⎰157分五.(本题8分)解:,,P x Q y R z ===1,1,1P Q R xyZ∂∂∂===∂∂∂ 1分x d y d zy d z d xz d x d yx d y d zy d z'∑∑+++++⎰⎰⎰⎰ =3dxdydz Ω⎰⎰⎰(其中'∑为平面0z =的下侧,Ω为'∑∑与围成的封闭区域) 4分=314323R π⨯⨯=32R π 5分又xdydz ydzdx zdxdy '∑++⎰⎰=0 7分则xdydz ydzdx zdxdy ∑++⎰⎰=32R π 8分六. (本题7分)21()56f x x x =++111(2)(323x x x x ==-++++=1111(1)2(1)2x x -++++2分而1(1)(1)201(1nnn x x x ∞==-+-<<++∑4分11(1)(1)311222(1)2nnnn x x x ∞=+=--<<++∑6分因此2111()(1)(1)(1)562nnn n f x x x x ∞+===--+++∑20x -<< 7分七.证明:()()()()f x g x g x f x ''==()()f x f x ''∴= 1212()()x xx x f x c e c e g xc ec e--=+=-2分04)()(2122≠=-c c x g x f 则21c c 与都不为零 又210)(c c x g 与∴≠是异号的常数不妨设0021<>c c 和 则-∞=+∞=+∞→+∞→)(lim )(lim x f x f x x()+∞∞-∴,)(在x f 内至少有一个实根 4分又)()(x g x f ='>0 )(x f ∴单调增加 0)(=∴x f 有且仅有一个实根 0)(≠x g 0)()(=∴x g x f 有且仅有一个实根0021><c c 和的情况同理可证. 6分。

2007-2008学年第一学期2007级电气、电子、工程管理、机制、教技、土木工程、计算机、农机、网络工程、物理专业高等数学Ⅰ 试卷A 参考答案一、填空题(填对每空得2分，填错或不填每空得0分，计20分) 1．982442424++++x x x x ．2．3-e．3． 3 ． 4． 3 ． 5． （ 0 ，-1 ）． 6．21．7．0144=++y x ．8．51．9． 0 ． 10．14．二、选择题（选对每题得2分，不选、选错或多选每题得0分，计10分） 1．（ D ） 2．（ B ） 3．（ C ） 4．（ A ） 5．（ B ）三、计算题（每小题5分，计20分）1．解： xx x x x x x x sin )sin 21(1lim sin 2cos 1lim 200--=-→→…………………………2分xx xx sin sin 2lim 20→= …………………………………3分 x xx sin 2lim0→=..........................................4分 2=． (5)分2．解：应用洛必达法则得xxx xtd t t x xx 2arctan limarctan lim20-=∞-→∞-→⎰………………………3分x x a r c t a nlim 21∞-→-= ………………………4分 4)2(21ππ=-⨯-=. ………………………5分3．解： ⎰dx xx2sin ⎰-=x xd cot ……………………………………1分 ⎰+-=xdx x x cot cot ， …………………………2分 ⎰+-=dx x x x x sin cos cot ……………………………3分 ⎰+-=x d x x x s i n s i n1c o t ………………………4分c x x x ++-=|s i n |ln cot ．………………………5分4．解： ⎰-+1021xx dx ⎰+=20cos sin cos sin πtt tdt tx ……………………………1分⎰++=202)cos (sin )cos (sin cos πt t dt t t t (2)分⎰+++=202sin 112cos 2sin 21πdttt t……………………3分⎰⎪⎭⎫ ⎝⎛++=202sin 12cos 121πdt t t ………………………4分 4)2sin 1ln(212120ππ=⎥⎦⎤⎢⎣⎡++=t t ．………………5分四、解答题（每小题5分，计20分） 1．解：)sin ()cos 1(t t ad t ad dxdy --= (1)分ttcos 1sin -=． …………………………………………2分)sin (cos 1sin 22t t ad t t d dxy d -⎪⎭⎫ ⎝⎛-= ………………………………………3分)cos 1()cos 1(sin )cos 1(cos 22t a t t t t ----=……………………………4分23)cos 1(1)cos 1(1cos t a t a t --=--=． …………………5分 2．解： 方程两边同时微分得)()(y x e d xy d += ………………………1分即 )(dy dx e xdy ydx y x +=++ ……………………3分 整理得 ydx dx e dy e xdy y x y x -=-++， …………………4分 从而得 dx ex yedy yx yx ++--=．……………………………5分3．解：令u e x=可得u x ln =，代入已知式得 ……………………………1分 u u f ln )(='， c u u u udu +-=⎰ln ln …………………2分 从而有 0ln )(c u u u u f +-= ……………………………………3分 由0)1(=f 得 10=c ……………………………………………4分 因此 1ln )(+-=x x x x f ． ……………………………………5分4．解：设所求平面的法线向量为0),,(≠=C B A n ，两个已知平面的法线向量分别为)4,2,1(,)2,5,3(21-=-=n n， ……………………………………1分则有n n n n⊥⊥21, 即有 ⎩⎨⎧=+-=-+0420253C B A C B A ………………………2分得 A C A B 1611,87-=-=，0≠A ……………………………………3分 所以所求平面的方程为 0)3(161187)2(=+---z A Ay x A ，………4分整理得所求平面的方程为 065111416=---z y x ． …………………5分五、证明题（6分×2题＝12分） 1．证明：由题设有hx f h x f x f h )()(lim)(0000-+='→，所以…………………1分hx f h x f x f h x f hh x f h x f h h )]()5([)()3(lim)5()3(lim 00000000----+=--+→→……………2分⎥⎦⎤⎢⎣⎡----+=→h x f h x f h x f h x f h )()5()()3(lim 00000…………3分hx f h x f h x f h x f h h 5)()5(lim53)()3(lim3000000---+-+=→→……5分)(8)(5)(3000x f x f x f '='+'=． (6)分2．证：设x x x x f -++=)1ln()1()(，则0)0(=f ，………………………1分 又 )1l n ()(x x f +='． ……………………………………………2分 当0>x 时， 0)(>'x f ，函数单调增加， ……………………3分当01<<-x 时， 0)(<'x f ，函数单调减少．………………………4分 从而，当01≠<-x 时有0)(>x f ，且0)0(=f ， ………………………5分因此，当1->x 时，x x x ≥++)1ln()1(． ……………………………6分六、综合应用题（6分×3题＝18分）解：由⎩⎨⎧=+-=022y x x y 得两曲线交点为)4,2(),1,1(-， …………………1分1．图形面积为 ⎰--+=212)2(dx x x A …………………………3分 29312212132=⎥⎦⎤⎢⎣⎡-+=-x x x ， …………………6分2．图形绕x 轴旋转一周所得旋转体的体积为⎰--+=21222])()2[(dx x x V x π……………………………9分 57251)2(312153ππ=⎥⎦⎤⎢⎣⎡-+=-x x ……………………12分3．曲线2x y =交y 轴于点)0,0(，直线02=+-y x 与y 交于点)2,0( ……………………………13分图形绕y 轴旋转一周所得旋转体的体积为⎰⎰--=4422)2(dy y ydy V y ππ， (15)分 316)2(32423402πππ=--=y y ； ………………………18分。

高等数学（一）、（二）（上）试题（A ）评分标准与分工一、 填空题（每小题4分, 共24分）1．e . 2． =a －１. 3．)4ln 2,2(+ .4．０ . 5． x e x C C y )(21+=）. 6.21=ξ注：该题评分原则是 非对即错二、选择题 (每小题4分, 共20分) D C BB C 三、（5分）解: 30sin tan sin limx x x x -→30tan sin lim xxx x -=→ x x x x x sin cos 1cos lim 30-=→22021lim xx x -=→21-= -------------------------------- 5分注：该题评分原则 体现方法3分、结果正确2分；主要有以下几种方法 1）洛必达法则、2）等价无穷小替换、3）其他 四、（8分）解: 212)111(22tt t tdtdxdt dy dx dt dt dy dx dy =++-==⋅=； ------------- 4分t t dt dx t dt d dx dy dx d dx y d 412222+=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=……. ------------- 4分 五、（8分）1）⎰-+x x e e dx ⎰+=xxede 21-------------------------------- 4分 C e x+=arctan -------------------------------- 4分2）. 解: ⎰⎰⎰⎰+=+=ππππ002200222]2cos [2122cos 1cos xdx x dx x dx x x xdx x ………2分 （第一个积分1分；第二个积分3分）⎰⎰⎰-==ππππ22122122122sin 0|2sin 2sin 2cos xdx x x x d x xdx x ………3分=⎰⎰=-=ππππ0022121212cos 0|2cos 2cos xdx x x x xd4361ππ+=∴原式 ……………………………………3分 注：本题主要考察学生对分部积分的内容的掌握情况。

河北科技大学2007——2008学年第一学期《质量管理》期末考试试卷（B´）学院班级姓名学号一、单选题(在每小题的备选答案中选出一个正确的答案，并将正确答案的号码填在题干的括号内。

每小题1分，共20分)1. 如果工序中存在形位偏差或某种加工习惯，则抽样所得直方图形状可能是（）。

A．平顶型B．偏向型C．双峰型D．孤岛型2. 生产要素的5M1E是指( )。

A．人、机、料、检、环、测B．人、检、料、法、测、机C．机、料、法、检、环、测D．人、机、料、法、测、环3. ( )是指国家质量监督机构站在第三方的立场上，公正地处理质量争议中的问题。

A．质量监督B．抽查型质量监督C．评价型质量监督D．仲裁型质量监督4.下列特性中属于汽车产品固有特性的是（）。

A．汽车的价格B．汽车交付的及时性C．汽车百公里耗油量D．汽车交付的方式5. 推动PDCA循环，关键在于( )。

A．计划阶段B．执行阶段C．检查阶段D．总结阶段6. 根据给定的技术标准，将单位产品的质量特性用连续尺度测量出其具体数值并与标准对比的检验为( )。

A．计量检验B．计点检验C．计数检验D．计件检验7. 质量管理的所有工作都是通过( )来实现的。

A．资源B．程序C．组织结构D．过程8. 在下列产品的可靠性设计中，相对来说更需要采用冗余技术的是( )。

A．汽车B．飞机C．摩托车D．火车9. 直方图定量表示的主要特征值标准差S越小，表明( )。

A．数据分散程度越小，加工精度越差B．数据分散程度越小，加工精度越好C．数据分散程度越大，加工精度越差D．数据分散程度越大，加工精度越好10. 在正态分布的情况下，质量特性值落在6σ范围内的概率为( )。

A．95.45% B．97.7% C．99.73% D．100% 1. 下面关于11. 全面质量管理与质量标准体系不同之处的叙述正确的是( )。

A．全面质量管理是静态要求，质量标准体系是动态要求B．全面质量管理是最基本的要求，质量标准体系是更高的要求C．全面质量管理是协商性、一致性要求，质量标准体系是差异性要求D．质量标准体系是最基本的要求，全面质量管理是更高的要求12. 我国有关产品质量的基本法律是( )。

河北科技大学2012——2013学年《高等数学》（上册）期末考试A 卷一. 单项选择题（每小题4分，共20分）1. 设λ是常数，函数⎪⎩⎪⎨⎧≤>--=1,01,11cos )1(1)(x x x x x g λ处处可微，则必有( )A.1-<λB. 01<≤-λC. 10<≤λD. λ≤12. 设函数⎪⎩⎪⎨⎧≥+<+=0,10,1sin cos )(2x x x xx x x f 则0=x 是函数()f x 的( ) A. 可去间断点 B. 跳跃间断点 C. 振荡间断点 D.连续点3. 已知函数()f x 二阶导数连续，且0)0(=f ，2)(lim 20-=-→x f x x ，则0)0(=f （ ） A.是函数)(x f 的极小值 B.是函数)(x f 的极大值C.不是函数)(x f 的极值D.不一定是函数)(x f 的极值4. 设在区间],[b a 上0)(>x f ，0)(<'x f ，0)(<''x f ，令))((1a b a f S -=， ))](2([2a b b a f S -+=，))](()([213a b b f a f S -+=，则 ( ) A. 321S S S << B. 312S S S << C. 123S S S << D. 213S S S <<5. 已知θae r =，则从0=θ到πθ=的弧长为( )A.)1(-πe aB. )1(2-πe aC. πae 2D. )1(2πe a -二.填空题（每小题4分，共20分）1. 设函数()f x 二阶导数连续，且0)(lim 0=+→x x f x ，2)0(=''f ，则=++→x x x x f 10])(1[l i m . 2. 函数x e x y +=sin 上点)1,0(处的法线方程是 .3. 设1arcsin )1()(+-+=x x x x x x f ，则=')1(f .4. 设曲线2x y =与直线2=x 及x 轴所围成的图形的面积为A ，则=A .5.⎰-=+-+225)cos |11|(ln ππdx x xx . 三. 计算下列各题：（每小题7分，共35分）1. 求极限⎰⎰+→022020)]1[ln(sin lim 2x x x dt t t dt t .2. 已知参数方程为⎩⎨⎧-=+=tt y t x arctan )1ln(2（其中t 为参数），求y ''.3. 设⎪⎩⎪⎨⎧<+≥+=--0,)1(0,)1()(11x e x x x f x ，求定积分⎰-20)1(dx x f 的值. 4. 求不定积分⎰-dx x x 2)(sin .5.求曲线311-+=x y 的凹凸区间及拐点.四．解答下列各题（第一小题9分，第二小题8分，共17分）1. 设函数)(x f 在),(+∞-∞内有定义，且1)0(='f ，对任意的数y x ,恒有等式 xy y f x f y x f 2)()()(++=+成立，求函数)(x f 的表达式.2. 求曲线2x y =在区间)1,0(内的一条切线，使该切线与直线0=x ，1=x 和曲线2x y =所围成图形的面积最小.五. 证明题（8分）设函数)(x f ，)(x g 二阶可导，且当0>x 时，)()(x g x f ''>''，又)0()0(g f =，)0()0(g f '='，证明：当0>x 时，恒有)()(x g x f >.。