2019年高三数学二轮复习试题：专题二 第1讲 三角恒等变换 含解析

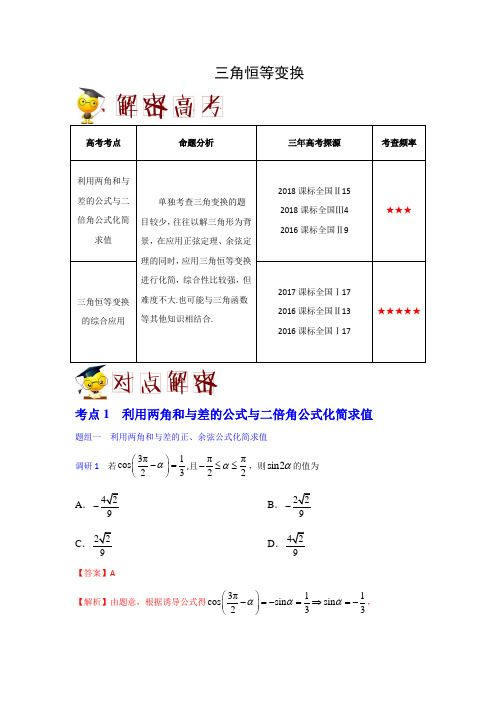
三角恒等变换考点1 利用两角和与差的公式与二倍角公式化简求值题组一 利用两角和与差的正、余弦公式化简求值 调研1，则sin2α的值为AB C ．9D ．9【答案】A又因为sin 0α<cos α=，所以1sin22sin cos 2339ααα⎛⎫==⨯-⨯=- ⎪⎝⎭， 故选A ．调研2 已知3π4πθ≤≤，且=，则θ=A B CD 【答案】D【名师点睛】此题考查了三角函数的化简求值，涉及的知识有：二倍角的余弦函数公式，两角和与差的正弦函数公式，以及绝对值的代数意义，熟练掌握公式是解本题的关键；根据α的范围求出2α的范围，确定出cos 02θ>，sin 02θ<，所求式子利用二倍角的余弦函数公式及绝对值的代数意义化简，再利用两角和与差的余弦函数，结合角的范围即可求出.☆技巧点拨☆三角恒等变换的“四大策略”：(1)常值代换：特别是“1”的代换，1＝sin 2θ＋cos 2θ＝tan 45° 等；(2)项的分拆与角的配凑：如sin 2α＋2cos 2α＝(sin 2α＋cos 2α)＋cos 2α，α＝(α－β)＋β等； (3)降次与升次：正用二倍角公式升次，逆用二倍角公式降次； (4)弦、切互化：一般是切化弦．题组二 利用两角和与差的正切公式化简求值调研3 若2tan 1α=，tan 2β=-，则()tan αβ+=__________． 【答案】34-【解析】()()121322tan 1tan tan 124122αααβ-=∴=∴+==--⨯-，，. 调研4 已知π,π2α⎛⎫∈⎪⎝⎭，tan 2α=-． （1）求πtan 4α⎛⎫+⎪⎝⎭的值． （2）求sin2cos2αα+的值． 【答案】（1）13-；（2）75-【解析】（1）∵tan 2α=-，∴()πtan tanπtan 12114tan π41tan 1231tan tan 4ααααα++-+⎛⎫+====- ⎪---⎝⎭-． （2）由π,π2α⎛⎫∈⎪⎝⎭，tan 2α=-，得sin α=，cos α=， ∴22437sin2cos22sin cos cos sin 555αααααα+=+-=--=-．【思路点拨】（1）利用两角和的正切公式可得结果； （2）根据角α的范围，由正切求出sin α=，cos α=，再利用二倍角公式即可得结果.☆技巧点拨☆公式的常见变形：（1）tan tan tan()(1tan tan )αβαβαβ±=±；tan tan tan tan tan tan 11tan()tan()αβαβαβαβαβ+-=-=-+-.（2）降幂公式：21cos 2sin2αα-=；21cos 2cos 2αα+=；1sin cos sin 22ααα=. （3）升幂公式：21cos 22cos αα+=；21cos 22sin αα-=；21sin 2(sin cos )ααα+=+；21sin 2(sin cos )ααα-=-.（4）辅助角公式：sin cos a x b x +)x ϕ=+，其中cos ϕϕ==tan baϕ=.考点2 三角恒等变换的综合应用题组一 与三角函数的图象及性质相结合 调研1 将函数()sin f x x =的图象向右平移π3个单位后得到函数()y g x =的图象,则函数()y f x =+()π,,π2g x x ⎡⎤∈⎢⎥⎣⎦的最小值为 .【解析】由题意得()πsin ,3g x x ⎛⎫=-⎪⎝⎭∴y =()()f x g x +=πsin sin 3x x ⎛⎫+-⎪⎝⎭=ππsin sin cos cos sin 33x x x +-=3sin 2x x -=π6x ⎛⎫- ⎪⎝⎭.π,π2x ⎡⎤∈⎢⎥⎣⎦,∴ππ5π ,636x ⎡⎤-∈⎢⎥⎣⎦,∴当π5π66x -=时,min y =调研 2 （安徽省A10联盟2019届高三11月段考数学试题）已知函数()225sin cos f x x x x +-.（1）求函数()f x 的单调递增区间； （2）求函数()2y f x =-在π7π,66⎡⎤⎢⎥⎣⎦上的零点. 【答案】（1）()π5ππ,π1212k k k ⎡⎤-++∈⎢⎥⎣⎦Z ；（2）π2π7π,,636.【解析】（1）()225sin cos f x x x x =+-()()511cos21cos222x x x =+--+3cos22x x =-+π223x ⎛⎫=-+ ⎪⎝⎭.令πππ2π22π,232k x k k -+≤-≤+∈Z ，得π5πππ,1212k x k k -+≤≤+∈Z ， ∴函数()f x 的单调递增区间为()π5ππ,π1212k k k ⎡⎤-++∈⎢⎥⎣⎦Z .（2）由()π2203f x x ⎛⎫-=-= ⎪⎝⎭，得：πsin 203x ⎛⎫-= ⎪⎝⎭. ∴()π2π3x k k -=∈Z ， ∴()1ππ26x k k =+∈Z ，∵π7π66x ≤≤， ∴π2π7π,,636x =，即函数()2y f x =-在π7π,66⎡⎤⎢⎥⎣⎦上的零点是π2π7π,,636.【名师点睛】本题考查了三角函数的恒等变换，考查了正弦型三角函数y =A sin （ωx +∅）的图象和性质，解答本题的关键是灵活应用二倍角的余弦公式和两角差的正弦公式将函数式化简为y =A sin （ωx +∅）+B 的形式.（1）利用三角函数关系式的恒等变换()π223f x x ⎛⎫=-+ ⎪⎝⎭，得，进而利用正弦函数的单调性，求出函数的单调递增区间；（2）将求函数()2y f x =-在π7π,66⎡⎤⎢⎥⎣⎦上的零点转化为求正弦型函数图象在π7π,66⎡⎤⎢⎥⎣⎦内与x 轴的交点，再根据正弦函数的性质求解. 题组二 与向量相结合调研3 已知()1cos ,1x ω=+-a ,)x ω=b (0ω>),函数()f x =⋅a b ,函数()f x 的最小正周期为2π． (1)求函数()f x 的表达式;(2)设π0,2θ⎛⎫∈ ⎪⎝⎭,且()65f θ=,求cos θ的值．【解析】(1)())1cos sin f x x x ωω=⋅+-a b π2sin 3x ω⎛⎫- ⎪⎝⎭, 因为函数()f x 的最小正周期为2π, 所以2π2πω=,解得1ω=,所以()π2sin 3f x x ⎛⎫=- ⎪⎝⎭．(2)由()65fθ=,得π3sin 35θ⎛⎫-=- ⎪⎝⎭,因为π0,2θ⎛⎫∈ ⎪⎝⎭,所以πππ,336θ⎛⎫-∈- ⎪⎝⎭, 所以π4cos 35θ⎛⎫-= ⎪⎝⎭,所以cos θ=ππcos 33θ⎛⎫-+ ⎪⎝⎭=ππππcos cos sin sin 3333θθ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=413525⎛⎫⨯-- ⎪⎝⎭=410+． 题组三 与解三角形相结合调研4 在ABC △中,角,,A B C 的对边分别为,,a b c ,且)3cos cos cos a A c B b C =+. （1）求tan2A 的值;（2）若πsin ,23B c ⎛⎫+==⎪⎝⎭求ABC △的面积.【答案】（1）（2）3.【解析】（1）由)3cos cos cos a A c B b C =+及正弦定理得 )()3sin cos sin cos sin cos A A C B B C B C A =+=+=， ∵sin 0A ≠，cos A ∴=∵π0,2A ⎛⎫∈ ⎪⎝⎭，sin 3A ∴=∴tan 2A =．22tan tan21tan AA A∴==-（2）由πsin 23B ⎛⎫+= ⎪⎝⎭得cos 3B = ∵()0,πB ∈，1sin 3B ∴=．∴()sin sin sin cos cos sin 3C A B A B A B =+=+= 由正弦定理得sin sin a c A C=，∴sin 2sin c Aa C===，∴△ABC的面积111sin 2223S ac B ==⨯⨯=． 【思路点拨】（1）由条件及正弦定理可得3sin cos A A A =，故cos 3A =，所以sin tan 32A A ==，由倍角公式可得tan2A = （2）由条件得cos 3B =，故得1sin 3B =，由正弦定理得2a =，从而可得△ABC的面积1sin 2S ac B ==． 【名师点睛】利用正、余弦定理求解三角形面积问题的题型与方法：(1)利用正弦、余弦定理解三角形，求出三角形的各个边、角后，直接求三角形的面积． (2)把面积作为已知条件之一，与正弦、余弦定理结合求出三角形的其他各量．(3)求三角形面积的最值或范围时，一般要先得到面积的表达式，再通过基本不等式、三角函数的求最值的方法求得面积的最值或范围．☆技巧点拨☆此类题中的角是在三角形中，每个角的范围限制在(0，π)内，如果是锐角三角形，则需要限制各个角均在π(0,)2内．角的范围在解题中至关重要，做题时要特别注意.1．（内蒙古呼和浩特市2018届高三年级质量普查调研考试数学试题）若()1sin π3α-=，且ππ2α≤≤，则sin2α的值为A ．B ．C D 2．（四川省资阳市2018-2019学年高三第一次诊断性考试数学试题）在直角坐标系xOy 中，角α的始边为x 轴的非负半轴，其终边上的一点P 的坐标为()2m m ，（其中0m <），则cos2α=A ．45 B ．35 C ．35-D ．45-3．（河南省八市学评2018届高三下学期第一次测评数学）已知2sin 23θ=，则2πtan 4θ⎛⎫-= ⎪⎝⎭A ．15B ．56C ．5D ．64．（江西省吉安一中、九江一中等八所重点中学2018届高三4月联考数学试题）若点(),0θ是函数()sin 2cos f x x x =+的图象的一个对称中心，则cos2sin cos θθθ+=A ．1110 B ．1110-C ．1D ．-15．（湖北省八校2018届高三上学期第一次联考（12月）数学试题）若αβ∈R ，且()πππ,π22k k k αβ≠+≠+∈Z ，则“2π+=3αβ”是“)114αβ--=”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．（福建省宁德市2018届高三下学期第二次（5月）质量检查数学试题）将周期为π的函数()ππcos (0)66f x x x ωωω⎛⎫⎛⎫=+++> ⎪ ⎪⎝⎭⎝⎭的图象向右平移π3个单位长度后，所得的函数解析式为 A ．π2sin 23y x ⎛⎫=-⎪⎝⎭B ．π2cos 23y x ⎛⎫=-⎪⎝⎭ C ．2sin2y x =D ．2π2cos 23y x ⎛⎫=-⎪⎝⎭7．（江西省上饶市2018届高三下学期第三次高考模拟考试数学试题）由射线43y x =（0x ≥）逆时针旋转到射线512y x =-（0x ≤）的位置所成角为θ，则cos θ= A ．1665-B ．1665±C ．5665-D ．5665±8．（四川省凉山州2019届高三第一次诊断性检测数学试题）设函数()πs i n c o s 4f x x x ⎛⎫=- ⎪⎝⎭，对任意x ∈R 都满足()()f c x f c x +=-，则c 的值可以是A ．π8 B ．3π8 C ．π2D ．5π89．（华大新高考联盟2018届高三4月教学质量检测试卷数学试题）锐角ABC △的外接圆半径为1，AC BC AB =>，且满足cos cos A C =C = A ．π12 B ．π6 C ．π4D ．5π1210．（山西省孝义市2018届高三下学期一模考试数学试题）已知函数()2cos2cos 1(0)222xxxf x ωωωω=+->的周期为π，当π0,2x ⎡⎤∈⎢⎥⎣⎦时，方程()f x m =恰有两个不同的实数解1x ，2x ，则()12f x x +=A ．2B ．1C ．1-D ．2-11．（河北省唐山市2018-2019学年高三上学期第一次摸底考试数学试题）已知函数()[]sin sin 3,0,2πf x x x x =-∈，则()f x 的所有零点之和等于A ．8πB ．7πC ．6πD ．5π12．（上海市杨浦区2018届高三下学期质量调研（二模）数学试题）若()()3sin cos cos sin 5x y x x y x ---=，则tan2y 的值为________.13．（四川省广安、眉山2018届毕业班第一次诊断性考试数学试题）已知π4cos 45α⎛⎫-= ⎪⎝⎭，则πsin 4α⎛⎫+= ⎪⎝⎭__________． 14．（黑龙江省大庆实验中学2019届高三上学期第一次月考数学试题）已知a ，b ，c 分别是△ABC 的三个内角A ，B ，C 所对的边，若c sin A ＝－a cos C A －cos 3π4B ⎛⎫+ ⎪⎝⎭的取值范围是________.15．（天津市静海区2019届高三上学期三校联考数学试题）已知函数()2π2cos 14f x x x ⎛⎫=-++ ⎪⎝⎭.（1）求()f x 的单调递增区间；（2）求()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的最值.16．（云南省曲靖市第一中学2019届高三高考复习质量监测三数学试题）已知()π11sin ,cos 453βαβ⎛⎫-=+=- ⎪⎝⎭，其中ππ0,022αβ<<<<.（1）求sin2β的值； （2）求πcos 4α⎛⎫+ ⎪⎝⎭的值.17．（江苏省清江中学2019届高三第二次教学质量调研数学试题）在△ABC 中，已知()22sin sin sin sin sin A B A C C -=-．（1）求内角B 的大小；（2）若cos 3A =，求sin 2C 的值．18．（广东省深圳实验、珠海一中等六校2019届高三第二次联考数学试题）已知向量)()2,1,sin ,cos x x x =-=m n ，函数()12f x =⋅+m n .（1）若()π0,,43x f x ⎡⎤∈=⎢⎥⎣⎦，求cos2x 的值；（2）在ABC △中，角,,A B C 对边分别是,,a b c ，且满足2cos 2b A c ≤，求()f B 的取值范围.19．（山西省吕梁市2019届高三上学期第一次阶段性测试数学试题）已知函数())()sin cos cos 02f x x x x ωωωω=-+>图象的一条对称轴为3π8x =． （1）求ω的最小值；（2）当ω取最小值时，若π3245f α⎛⎫+= ⎪⎝⎭，π02α-<<π2+4α⎛⎫ ⎪⎝⎭的值．1．（2018新课标全国Ⅲ理科）若1sin 3α=，则cos2α=A ．89B ．79 C ．79-D ．89-2．（2016新课标全国Ⅱ理科）若cos(4π−α)=53，则sin 2α= A ．725 B ．15C ．−15D ．−7253．（2018新课标全国Ⅱ理科）已知sin cos 1αβ+=，cos sin 0αβ+=，则s i n()αβ+=__________．4．（2016新课标全国Ⅱ理科）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，若cos A =45，cos C =513，a =1，则b = . 5．（2016新课标全国Ⅰ理科）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，已知2cos (cos cos ).C a B+b A c =（I ）求C ；（II ）若c ABC △=ABC △的周长．6． （2017新课标全国Ⅰ理科）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，已知ABC△的面积为23sin a A. （1）求sin B sin C ;（2）若6cos B cos C =1，a =3，求ABC △的周长.三角恒等变换考点1 利用两角和与差的公式与二倍角公式化简求值题组一 利用两角和与差的正、余弦公式化简求值 调研1，则sin2α的值为ABC ．9D ．9【答案】A又因为sin 0α<cos 3α=， 所以1sin22sincos 2339ααα⎛⎫==⨯-⨯=- ⎪⎝⎭， 故选A ．调研2 已知3π4πθ≤≤，且2=，则θ=ABCD 【答案】D【名师点睛】此题考查了三角函数的化简求值，涉及的知识有：二倍角的余弦函数公式，两角和与差的正弦函数公式，以及绝对值的代数意义，熟练掌握公式是解本题的关键；根据α的范围求出2α的范围，确定出cos 02θ>，sin 02θ<，所求式子利用二倍角的余弦函数公式及绝对值的代数意义化简，再利用两角和与差的余弦函数，结合角的范围即可求出.☆技巧点拨☆三角恒等变换的“四大策略”：(1)常值代换：特别是“1”的代换，1＝sin 2θ＋cos 2θ＝tan 45° 等；(2)项的分拆与角的配凑：如sin 2α＋2cos 2α＝(sin 2α＋cos 2α)＋cos 2α，α＝(α－β)＋β等； (3)降次与升次：正用二倍角公式升次，逆用二倍角公式降次； (4)弦、切互化：一般是切化弦．题组二 利用两角和与差的正切公式化简求值调研3 若2tan 1α=，tan 2β=-，则()tan αβ+=__________． 【答案】34-【解析】()()121322tan 1tan tan 124122αααβ-=∴=∴+==--⨯-，，. 调研4 已知π,π2α⎛⎫∈⎪⎝⎭，tan 2α=-． （1）求πtan 4α⎛⎫+⎪⎝⎭的值． （2）求sin2cos2αα+的值． 【答案】（1）13-；（2）75-【解析】（1）∵tan 2α=-，∴()πtan tanπtan 12114tan π41tan 1231tan tan 4ααααα++-+⎛⎫+====- ⎪---⎝⎭-．（2）由π,π2α⎛⎫∈⎪⎝⎭，tan 2α=-， 得sinα=，cos α=， ∴22437sin2cos22sin cos cos sin 555αααααα+=+-=--=-．【思路点拨】（1）利用两角和的正切公式可得结果； （2）根据角α的范围，由正切求出sinα=，cos α=，再利用二倍角公式即可得结果.☆技巧点拨☆公式的常见变形：（1）tan tan tan()(1tan tan )αβαβαβ±=±；tan tan tan tan tan tan 11tan()tan()αβαβαβαβαβ+-=-=-+-.（2）降幂公式：21cos 2sin 2αα-=；21cos 2cos 2αα+=；1sin cos sin 22ααα=. （3）升幂公式：21cos 22cos αα+=；21cos 22sin αα-=；21sin 2(sin cos )ααα+=+；21sin 2(sin cos )ααα-=-.（4）辅助角公式：sin cos a x b x +)x ϕ=+，其中cos ϕϕ==tan baϕ=.考点2 三角恒等变换的综合应用题组一 与三角函数的图象及性质相结合调研1 将函数()sin f x x =的图象向右平移π3个单位后得到函数()y g x =的图象,则函数()y f x =+()π,,π2g x x ⎡⎤∈⎢⎥⎣⎦的最小值为 .【解析】由题意得()πsin ,3g x x ⎛⎫=- ⎪⎝⎭∴y =()()f x g x +=πsin sin 3x x ⎛⎫+-⎪⎝⎭=ππsin sin cos cos sin 33x x x +-=3sin 2x x -=π6x ⎛⎫- ⎪⎝⎭. π,π2x ⎡⎤∈⎢⎥⎣⎦,∴ππ5π ,636x ⎡⎤-∈⎢⎥⎣⎦,∴当π5π66x -=时,min y =调研 2 （安徽省A10联盟2019届高三11月段考数学试题）已知函数()225sin cos f x x x x +-.（1）求函数()f x 的单调递增区间； （2）求函数()2y f x =-在π7π,66⎡⎤⎢⎥⎣⎦上的零点. 【答案】（1）()π5ππ,π1212k k k ⎡⎤-++∈⎢⎥⎣⎦Z ；（2）π2π7π,,636.【解析】（1）()225sin cos f x x x x =+-()()511cos21cos222x x x =+--+3cos22x x =-+π223x ⎛⎫=-+ ⎪⎝⎭.令πππ2π22π,232k x k k -+≤-≤+∈Z ，得π5πππ,1212k x k k -+≤≤+∈Z ， ∴函数()f x 的单调递增区间为()π5ππ,π1212k k k ⎡⎤-++∈⎢⎥⎣⎦Z .【名师点睛】本题考查了三角函数的恒等变换，考查了正弦型三角函数y =A sin （ωx +∅）的图象和性质，解答本题的关键是灵活应用二倍角的余弦公式和两角差的正弦公式将函数式化简为y =A sin （ωx +∅）+B 的形式.（1）利用三角函数关系式的恒等变换()π223f x x ⎛⎫=-+ ⎪⎝⎭，得，进而利用正弦函数的单调性，求出函数的单调递增区间； （2）将求函数()2y f x =-在π7π,66⎡⎤⎢⎥⎣⎦上的零点转化为求正弦型函数图象在π7π,66⎡⎤⎢⎥⎣⎦内与x 轴的交点，再根据正弦函数的性质求解. 题组二 与向量相结合调研3 已知()1cos ,1x ω=+-a ,)x ω=b (0ω>),函数()f x =⋅a b ,函数()f x 的最小正周期为2π． (1)求函数()f x 的表达式;(2)设π0,2θ⎛⎫∈ ⎪⎝⎭,且()65f θ=,求cos θ的值．【解析】(1)())1cos sin f x x x ωω=⋅+-a b π2sin 3x ω⎛⎫- ⎪⎝⎭, 因为函数()f x 的最小正周期为2π, 所以2π2πω=,解得1ω=,所以()π2sin 3f x x ⎛⎫=-⎪⎝⎭．(2)由()65fθ=,得π3sin 35θ⎛⎫-=- ⎪⎝⎭,因为π0,2θ⎛⎫∈ ⎪⎝⎭,所以πππ,336θ⎛⎫-∈- ⎪⎝⎭, 所以π4cos 35θ⎛⎫-= ⎪⎝⎭,所以cos θ=ππcos 33θ⎛⎫-+ ⎪⎝⎭=ππππcos cos sin sin 3333θθ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=4135252⎛⎫⨯--⨯ ⎪⎝⎭． 题组三 与解三角形相结合调研4 在ABC △中,角,,A B C 的对边分别为,,a b c ,且)3cos cos cos a A c B b C =+. （1）求tan2A 的值;（2）若πsin ,23B c ⎛⎫+==⎪⎝⎭求ABC △的面积.【答案】（1）（2.【解析】（1）由)3cos cos cos a A c B b C =+及正弦定理得 )()3sin cos sin cos sin cos A A C B B C B C A =+=+=， ∵sin 0A ≠，cos A ∴=∵π0,2A ⎛⎫∈ ⎪⎝⎭，sin 3A ∴=∴tan 2A =．22tan tan21tan AA A∴==-（2）由πsin 2B ⎛⎫+=⎪⎝⎭得cos 3B = ∵()0,πB ∈，1sin 3B ∴=． ∴()sin sin sin cos cos sin C A B A B A B =+=+= 由正弦定理得sin sin a cA C=，∴sin 2sin c Aa C===，∴△ABC的面积111sin 2223S ac B ==⨯⨯=． 【思路点拨】（1）由条件及正弦定理可得3sin cos A A A =，故cos A =，所以sin tan 32A A ==，由倍角公式可得tan2A = （2）由条件得cos 3B =，故得1sin 3B =，由正弦定理得2a =，从而可得△ABC的面积1sin 23S ac B == 【名师点睛】利用正、余弦定理求解三角形面积问题的题型与方法：(1)利用正弦、余弦定理解三角形，求出三角形的各个边、角后，直接求三角形的面积． (2)把面积作为已知条件之一，与正弦、余弦定理结合求出三角形的其他各量．(3)求三角形面积的最值或范围时，一般要先得到面积的表达式，再通过基本不等式、三角函数的求最值的方法求得面积的最值或范围．☆技巧点拨☆此类题中的角是在三角形中，每个角的范围限制在(0，π)内，如果是锐角三角形，则需要限制各个角均在π(0,)2内．角的范围在解题中至关重要，做题时要特别注意.1．（内蒙古呼和浩特市2018届高三年级质量普查调研考试数学试题）若()1sin π3α-=，且ππ2α≤≤，则sin2α的值为A ．B ．C D 【答案】B【解析】∵()1sin πsin 3αα-==，ππ2α≤≤，∴cos 3α==-，∴1sin22sin cos 2339ααα⎛==⨯⨯-=- ⎝⎭. 故选B.2．（四川省资阳市2018-2019学年高三第一次诊断性考试数学试题）在直角坐标系xOy 中，角α的始边为x 轴的非负半轴，其终边上的一点P 的坐标为()2m m ，（其中0m <），则cos2α=A ．45 B ．35 C ．35-D ．45-【答案】B【解析】0,m P <∴在第三象限，且r =，由正弦函数的定义可得sin5α==-，223cos212sin 155αα∴=-=-=.故选B.【名师点睛】本题主要考查三角函数的定义以及二倍角的余弦公式，意在考查综合运用所学知识解决问题的能力，属于中档题.利用三角函数的定义求出sin α的值，由二倍角的余弦公式可得结果.3．（河南省八市学评2018届高三下学期第一次测评数学）已知2sin 23θ=，则2πtan 4θ⎛⎫-= ⎪⎝⎭A ．15B ．56C ．5D ．6【答案】A【解析】由题意可知ππ2sin2cos 2cos 2243θθθ⎡⎤⎛⎫⎛⎫=-=-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦， 则22π2π52cos 1cos 4346θθ⎛⎫⎛⎫--=⇒-=⎪ ⎪⎝⎭⎝⎭，22π2π112sin sin 4346θθ⎛⎫⎛⎫--=⇒-= ⎪ ⎪⎝⎭⎝⎭，所以222πsin π14tan π45cos 4θθθ⎛⎫- ⎪⎛⎫⎝⎭-== ⎪⎛⎫⎝⎭- ⎪⎝⎭.故选A ．4．（江西省吉安一中、九江一中等八所重点中学2018届高三4月联考数学试题）若点(),0θ是函数()sin 2cos f x x x =+的图象的一个对称中心，则cos2sin cos θθθ+=A ．1110 B ．1110-C ．1D ．−1【答案】D5．（湖北省八校2018届高三上学期第一次联考（12月）数学试题）若αβ∈R ，且()πππ,π22k k k αβ≠+≠+∈Z ，则“2π+=3αβ”是“)114αβ--=”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A【解析】)114αβ--=，即3tan tan 14αβαβ+=，tan tan tan αβαβ--=即t a n t a n 1t a n t a n αβαβ+=-即()t a n αβ+=所以2ππ3k αβ+=+，当0k =时，2π3αβ+=，所以“2π3αβ+=”是“)114αβ--=”的充分不必要条件.故选A.【名师点睛】本题考查切化弦公式，两角和的正余弦公式，充分不必要条件的概念，已知三角函数值求角，属于中档题. 根据切化弦公式，两角和的正余弦公式将原等式化成：()tan αβ+=，这便可求出2ππ3k αβ+=+，这样便会得到2π3αβ+=是)114αβ--=充分不必要条件．6．（福建省宁德市2018届高三下学期第二次（5月）质量检查数学试题）将周期为π的函数()ππcos (0)66f x x x ωωω⎛⎫⎛⎫=+++> ⎪ ⎪⎝⎭⎝⎭的图象向右平移π3个单位长度后，所得的函数解析式为 A ．π2sin 23y x ⎛⎫=-⎪⎝⎭B ．π2cos 23y x ⎛⎫=-⎪⎝⎭ C ．2sin2y x =D ．2π2cos 23y x ⎛⎫=-⎪⎝⎭【答案】A【名师点睛】（1）本题主要考查三角函数解析式的求法，考查函数图象的变换，意在考查学生对这些基础知识的掌握能力.先化简f (x )，再求出ω的值，再求平移后的函数解析式得解. （2）把函数()f x 的图象向右平移(0)a a >个单位，得到函数()f x a -的图象，把函数()f x 的图象向左平移(0)a a >个单位，得到函数()f x a +的图象,简记为“左加右减”.7．（江西省上饶市2018届高三下学期第三次高考模拟考试数学试题）由射线43y x =（0x ≥）逆时针旋转到射线512y x =-（0x ≤）的位置所成角为θ，则cos θ= A ．1665- B ．1665±C ．5665-D ．5665±【答案】A【解析】设43y x =（0x ≥）的倾斜角为α，则43sin cos 55αα==，， 射线512y x =-（0x ≤）的倾斜角为β，则512sin cos 1313ββ==-，，∴()3124516cos cos cos cos sin sin ()51351365θβααβαβ=-=+=⨯-+⨯=-.故选A.【名师点睛】本题主要考查了三角函数的定义及两角差的余弦函数公式，考查了逻辑推理能力与运算求解能力，属于中档题.8．（四川省凉山州2019届高三第一次诊断性检测数学试题）设函数()πs i n c o s 4f x x x ⎛⎫=- ⎪⎝⎭，对任意x ∈R 都满足()()f c x f c x +=-，则c 的值可以是A ．π8 B ．3π8 C ．π2D ．5π8【答案】B【解析】函数()πsin cos sin cos 44224f x x x x x x ⎛⎫⎛⎫=--=+- ⎪ ⎪ ⎪⎝⎭⎝⎭2244x x =-1πsin 224x ⎛⎫=- ⎪⎝⎭， 对任意x ∈R 都满足()()f c x f c x +=-，即x c =为函数图象的对称轴.令ππ22π,42x k k -=+∈Z ，解得3ππ,8x k k =+∈Z . 当0k =时，3π8x =.故选B.【名师点睛】本题主要考查了两角差的余弦展开公式、二倍角公式、辅助角公式及三角函数的对称性，属于中档题.化简函数得()1πsin 224f x x ⎛⎫=- ⎪⎝⎭，由()()f c x f c x +=-，得x c =为函数图象的对称轴，令ππ22π,42x k k -=+∈Z 解出对称轴即可得解. 9．（华大新高考联盟2018届高三4月教学质量检测试卷数学试题）锐角ABC △的外接圆半径为1，AC BC AB =>，且满足1cos cos 4A C =，则C = A ．π12 B ．π6 C ．π4D ．5π12【答案】C【解析】因为ππsin 0,,.23B B B ⎛⎫==∈∴= ⎪⎝⎭因为1cos cos 4A C =，所以22π113c o s co s,3422C C C C C⎛⎫-=∴-+= ⎪⎝⎭即1πcos 22246C C C ⎛⎫-=-=⎪⎝⎭， 因此ππ2=63C -或π2π2=63C -，即π=4C 或5π=12C ， 因为BC AB >，所以π3C <，即π=4C .故选C.10．（山西省孝义市2018届高三下学期一模考试数学试题）已知函数()2cos2cos 1(0)222xxxf x ωωωω=+->的周期为π，当π0,2x ⎡⎤∈⎢⎥⎣⎦时，方程()f x m =恰有两个不同的实数解1x ，2x ，则()12f x x +=A ．2B ．1C ．1-D ．2-【答案】B【解析】函数()2cos2cos 1222xxxf x ωωω=+-πcos 2sin 6x x x ωωω⎛⎫=+=+ ⎪⎝⎭，由周期2ππT ω==，可得()π2,2sin 26f x x ω⎛⎫=∴=+ ⎪⎝⎭，πππ7π0,,22666x x ⎡⎤∈∴≤+≤⎢⎥⎣⎦，()12f x ∴-≤≤，且()f x 的对称轴为π6x =，方程()f x m =恰有两个不同的实数解12,x x ，12π3x x ∴+=，则()12π2ππ5π2sin 2sin 13366f x x f ⎛⎫⎛⎫+==+== ⎪ ⎪⎝⎭⎝⎭. 故选B.11．（河北省唐山市2018-2019学年高三上学期第一次摸底考试数学试题）已知函数()[]sin sin 3,0,2πf x x x x =-∈，则()f x 的所有零点之和等于A ．8πB ．7πC ．6πD ．5π【答案】B【解析】由已知函数()[]sin sin3,0,2πf x x x x =-∈，令()0f x =，即sin sin30x x -=，即2sin sin3sin cos2cos sin2sin cos22sin cos x x x x x x x x x x ==+=+， 即()2sin cos22cos 10x x x +-=，解得sin 0x =或2cos22cos 10x x +-=， 当[]sin 0,0,2πx x =∈时，0x =或πx =或2πx =；当2cos22cos 10x x +-=时，即222cos 2cos 20x x +-=，解得cos x =±， 又由[]0,2πx ∈，解得π4x =或3π4或5π4或7π4， 所以函数()f x 的所有零点之和为π3π5π7π0π2π7π4444++++++=. 故选B.【名师点睛】本题主要考查了函数的零点问题的综合应用，其中解答中熟记函数的零点的概念，以及熟练应用三角函数恒等变换的公式，求解方程的根是解得关键，试题有一定的难度，属于中档试题，着重考查了分析问题和解答问题的能力，以及推理与运算能力.根据函数的零点的定义，令()0f x =，得sin sin30x x -=，根据三角恒等变换的公式，求解方程的根，即可得到所有的零点之和，得到答案.12．（上海市杨浦区2018届高三下学期质量调研（二模）数学试题）若()()3sin cos cos sin 5x y x x y x ---=，则tan2y 的值为________.【答案】247±【解析】由已知有()3sin 5x y x ⎡⎤--=⎣⎦，即3sin 5y =-，y ∴为第三或第四象限的角. 当y 为第三象限的角时，3tan 4y =，则22tan 24tan 21tan 7y y y ==-； 当y 为第四象限的角时，3tan 4y =-，则22tan 24tan 21tan 7y y y ==--，24tan 27y ∴=±. 13．（四川省广安、眉山2018届毕业班第一次诊断性考试数学试题）已知π4cos 45α⎛⎫-= ⎪⎝⎭，则πsin 4α⎛⎫+= ⎪⎝⎭__________． 【答案】45【解析】)π4cos cos sin 45ααα⎛⎫-=+= ⎪⎝⎭，所以)π4sin sin cos 425ααα⎛⎫+=+= ⎪⎝⎭.故答案为45. 14．（黑龙江省大庆实验中学2019届高三上学期第一次月考数学试题）已知a ，b ，c 分别是△ABC 的三个内角A ，B ，C 所对的边，若c sin A ＝－a cos C A －cos 3π4B ⎛⎫+ ⎪⎝⎭的取值范围是________.【答案】⎛ ⎝⎭【解析】因为c sin A ＝－a cos C ，所以sin C sin A =-sin A cos C ，所以tan C =-1，即C =3π4.A －cos 3π4B ⎛⎫+ ⎪⎝⎭sin A +cos A =2sin(A +π6)，因为πππ5π1π0,,sin 46612264A A A ⎛⎫<<∴<+<∴<+< ⎪⎝⎭所以π12sin 62A ⎛⎫<+< ⎪⎝⎭.故答案为⎛⎝⎭. 【名师点睛】(1)本题主要考查正弦定理，考查三角恒等变换和三角函数的图象和性质，意在考查学生对这些知识的掌握水平和分析推理计算能力.先利用正弦定理求出∠C ,再化A －cos 3π4B ⎛⎫+⎪⎝⎭得2sin(A +π6)，再利用三角函数的图象和性质求解. (2)对于复合函数的问题自然是利用复合函数的性质解答，求复合函数的最值，一般从复合函数的定义域入手，结合三角函数的图象一步一步地推出函数()sin y A wx hφ=++的最值.15．（天津市静海区2019届高三上学期三校联考数学试题）已知函数()2π2cos 14f x x x ⎛⎫=-++ ⎪⎝⎭.（1）求()f x 的单调递增区间；（2）求()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的最值.【答案】（1）()5πππ,π1212k k k ⎡⎤-+∈⎢⎥⎣⎦Z ；（2）最大值为2，最小值为.【解析】（1）函数()2ππ2cos 1cos 242f x x x x x ⎛⎫⎛⎫=-++=-+ ⎪ ⎪⎝⎭⎝⎭sin2x x =+π2sin 23x ⎛⎫=+ ⎪⎝⎭.令πππ2π22π,232k x k k -≤+≤+∈Z ，解得5ππππ,1212k x k k -≤≤+∈Z ， ∴()f x 的单调递增区间为()5πππ,π+1212k k k ⎡⎤-∈⎢⎥⎣⎦Z . （2）当π0,2x ⎡⎤∈⎢⎥⎣⎦时，ππ4π2,333x ⎡⎤+∈⎢⎥⎣⎦，∴πsin 2,132x ⎡⎤⎛⎫+∈-⎢⎥ ⎪⎝⎭⎣⎦，∴()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值为2，最小值为且π12x =时()f x 取得最大值2，π2x =时()f x 取得最小值【名师点睛】本题主要考查辅助角公式、二倍角的余弦公式以及正弦函数的单调性，属于中档题. 函数()sin y A x ωϕ=+（0,0A ω>>）的单调区间的求法：把x ωϕ+看作是一个整体，由π2π2k x ωϕ+≤+≤()3π2π2k k +∈Z 求得函数的减区间；由ππ2π2π22k x k ωϕ-+≤+≤+求得函数的增区间. （1）利用二倍角公式以及两角和的正弦公式将函数()f x 化为π2sin 23x ⎛⎫+ ⎪⎝⎭，利用正弦函数的单调性解不等式，可得到函数()f x 的递增区间；（2）当π0,2x ⎡⎤∈⎢⎥⎣⎦时，ππ4π2,333x ⎡⎤+∈⎢⎥⎣⎦，由正弦函数的单调性可得πsin 232x ⎡⎤⎛⎫+∈-⎢⎥ ⎪⎝⎭⎣⎦，从而可得结果.16．（云南省曲靖市第一中学2019届高三高考复习质量监测三数学试题）已知()π11sin ,cos 453βαβ⎛⎫-=+=- ⎪⎝⎭，其中ππ0,022αβ<<<<.（1）求sin2β的值；（2）求πcos 4α⎛⎫+⎪⎝⎭的值. 【答案】（1）2325；（2）215.【解析】（1）因为()π1sin sin cos 425βββ⎛⎫-=-= ⎪⎝⎭，所以sin cos 5ββ-=， 所以()2222sin cos sin cos 2sin cos 1sin225βββββββ-=+-=-=， 所以23sin225β=． （2）因为π1sin 45β⎛⎫-= ⎪⎝⎭，()1cos 3αβ+=-，其中π02α<<，π02β<<，()πcos sin 453βαβ⎛⎫∴-=+=⎪⎝⎭， 所以()ππc o s44ααββ⎡⎤⎛⎫⎛⎫+=+-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦()()ππco s co44αββαββ⎛⎫⎛⎫=+-++- ⎪ ⎪⎝⎭⎝⎭21133515⎛⎫=-+= ⎪⎝⎭．【名师点睛】在解决三角中的给值求值问题时，解题的关键往往是要进行角的变换，将已知条件作为整体进行求解；同时在运用平方关系求三角函数值时，要注意所得结果的符号．（1）由π1sin 45β⎛⎫-= ⎪⎝⎭，可得sin cos 5ββ-=，两边平方后可得所求． （2）根据题意求出()πcos sin 43βαβ⎛⎫-=+= ⎪⎝⎭，然后根据()ππc o s c o s 44ααββ⎡⎤⎛⎫⎛⎫+=+-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦求解即可．17．（江苏省清江中学2019届高三第二次教学质量调研数学试题）在△ABC 中，已知()22sin sin sin sin sin A B A C C -=-．（1）求内角B 的大小；（2）若cos A =，求sin 2C 的值．【答案】（1）π3B =；（2）6.【解析】（1）在ABC △中，设,,A B C 的对边分别为,,a b c ， 由正弦定理sin sin sin a b c A B C==及()22sin sin sin sin sin A B A C C -=-得，222a b a c c -=-，即222a c b ac +-=，由余弦定理得2221cos 22a cb B ac +-==， 因为0πB <<， 所以π3B =. 【名师点睛】本题主要考查正弦定理、余弦定理解三角形，考查三角恒等变换求值，意在考查学生对这些知识的掌握水平和分析推理能力.（1）由正弦定理得222a c b ac +-=，再利用余弦定理化简得π3B =. （2）先求出sin2A ，cos2A ，再求sin2C .18．（广东省深圳实验、珠海一中等六校2019届高三第二次联考数学试题）已知向量)()2,1,sin ,cos x x x =-=m n ，函数()12f x =⋅+m n .（1）若()π0,,43x f x ⎡⎤∈=⎢⎥⎣⎦，求cos2x 的值；（2）在ABC △中，角,,A B C 对边分别是,,a b c ，且满足2cos 2b A c ≤，求()f B 的取值范围.【答案】（1）2-；（2）11,22⎛⎤- ⎥⎝⎦.【解析】（1）由题意知()21cos cos 2f x x x x =-+1cos22x x =-πsin 26x ⎛⎫=- ⎪⎝⎭.∴πsin 263x ⎛⎫-= ⎪⎝⎭. 又π0,4x ⎡⎤∈⎢⎥⎣⎦，πππ2663x ∴-≤-≤，πcos 263x ⎛⎫∴-=⎪⎝⎭， ππcos2cos 266x x ⎡⎤⎛⎫∴=-+ ⎪⎢⎥⎝⎭⎣⎦ππ1cos 2sin 2662x x ⎛⎫⎛⎫=---⨯ ⎪ ⎪⎝⎭⎝⎭12=-=（2）由2co s 23b A c ≤，得222222b c a b c bc+-⋅≤，即222a c b +-≥，222cos 22a cb B ac +-∴=≥，()0,π,B ∈π06B ∴<≤, 从而得πππ2666B -<-≤，故()π11sin 2,622f B B ⎛⎫⎛⎤=-∈- ⎪ ⎥⎝⎭⎝⎦. 【名师点睛】本题考查了三角恒等变换、三角函数求值及解三角形，考查了学生的化简运算能力，属于中档题．（1）利用三角恒等变换化简可得()πsin 263f x x ⎛⎫=-= ⎪⎝⎭，从而可得πcos 26x ⎛⎫-=⎪⎝⎭cos2x 的值；（2）化简可得222222222b c a b c c b bc+-⋅≤+-≥，从而可得222cos 22a cb B bc +-=≥，从而解得()f B 的取值范围．19．（山西省吕梁市2019届高三上学期第一次阶段性测试数学试题）已知函数())()sin cos cos 02f x x x x ωωωω=-+>图象的一条对称轴为3π8x =． （1）求ω的最小值；（2）当ω取最小值时，若π3245f α⎛⎫+= ⎪⎝⎭，π02α-<<π2+4α⎛⎫ ⎪⎝⎭的值．【答案】（1）1；（2）1725.【解析】（1）由题意得())sin cos cos f x x x x ωωω=-+2cos 2x x x ωωω=+sin2cos222x x ωω=- πsin 24x ω⎛⎫=- ⎪⎝⎭．因为函数()y f x =的一条对称轴为3π8x =，所以()3ππππ442k k ω-=+∈Z ， 所以()413k k ω=+∈Z ，又0ω>，所以ω的最小值为1．（2）由（1）知()πsin 24f x x ⎛⎫=-⎪⎝⎭．∴ππππ3sin 2sin 2424445f ααα⎡⎤⎛⎫⎛⎫⎛⎫+=+-=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦．∵π02α-<<， ∴π4cos 45α⎛⎫+= ⎪⎝⎭，πππππ2+2sin2cos244444αααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+-=+-+ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 23441722155525⎛⎫=⨯⨯-⨯+= ⎪⎝⎭．【思路分析】（1）由题意得()πsin 24f x x ω⎛⎫=- ⎪⎝⎭，又函数()f x 图象的一条对称轴为3π8x =，所以()3ππππ442k k ω-=+∈Z ，根据条件可得所求； （2）由（1）知()πsin 24f x x ⎛⎫=-⎪⎝⎭，可得π3245f α⎛⎫+= ⎪⎝⎭，根据同角关系可得π4cos 45α⎛⎫+= ⎪⎝⎭πππ2+2444αα⎡⎤⎛⎫⎛⎫=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦求解可得所求的结果．【名师点睛】（1）解答形如()siny A x ωϕ=+的函数的问题时，需要把x ωϕ+作为一个整体，并结合正弦函数的相关性质求解，解题时注意,A ω的符号对结果的影响． （2）在解答“给值求值”型的问题时，要注意角的变换，通过“拆”、“凑”等方法将所求角用已知角表示出来，然后再将所给条件作为整体进行求解．1．（2018新课标全国Ⅲ理科）若1sin 3α=，则cos2α=A ．89B ．79C ．79-D ．89-【答案】B【解析】2217cos 212sin12()39αα=-=-⨯=.故选B.【名师点睛】本题主要考查三角函数的求值，考查考生的运算求解能力，考查的核心素养是数学运算.2．（2016新课标全国Ⅱ理科）若cos(4π−α)=53，则sin 2α= A ．725 B ．15 C ．−15D ．−725【答案】D【解析】2237cos 22cos 12144525αα⎡π⎤π⎛⎫⎛⎫⎛⎫-=--=⨯-=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，又cos 2cos(2)sin 242ααα⎡π⎤π⎛⎫-=-=⎪⎢⎥⎝⎭⎣⎦，所以7sin 225α=-，故选D ．【名师点睛】对于三角函数的给值求值问题，关键是把待求角用已知角表示： (1)已知角为两个时，待求角一般表示为已知角的和或差．(2)已知角为一个时，待求角一般与已知角成“倍的关系”或“互余、互补”关系．3．（2018新课标全国Ⅱ理科）已知sin cos 1αβ+=，cos sin 0αβ+=，则s i n()αβ+=__________．【答案】【解析】因为，，所以，因此4．（2016新课标全国Ⅱ理科）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，若cos A =45，cos C =513，a =1，则b = . 【答案】2113【解析】因为45cos ,cos 513A C ==，且,A C 为三角形的内角，所以312sin ,sin 513A C ==，63sin sin[π()]sin()sin cos cos sin 65B AC A C A C A C =-+=+=+=，又因为sin sin a b A B =，所以sin 21sin 13a Bb A ==.【名师点睛】在解有关三角形的题目时，要有意识地考虑用哪个定理更适合，或是两个定理都要用，要抓住能够利用某个定理的信息．一般地，如果式子中含有角的余弦或边的二次式时，要考虑用余弦定理；如果式子中含有角的正弦或边的一次式时，则考虑用正弦定理；以上特征都不明显时，则要考虑两个定理都有可能用到．5．（2016新课标全国Ⅰ理科）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，已知2cos (cos cos ).C a B+b A c =（I ）求C ；（II ）若c ABC △=的面积为2，求ABC △的周长．【答案】（I ）π3；（II ）5． 【解析】（I ）由已知及正弦定理得()2cos sin cos sin cos sin C ΑΒΒΑC +=，()2cos sin sin C ΑΒC +=．故2sin cos sin C C C =． 可得1cos 2C =，所以π3C =．（II ）由已知，1sin 22ab C =． 又π3C =，所以6ab =． 由已知及余弦定理得，222cos 7a b ab C +-=． 故2213a b +=，从而()225a b +=．所以ΑΒC △的周长为5+．【名师点睛】三角形中的三角变换常用到诱导公式,()()sin sin ,cos cos ,A B C A B C +=+=- ()tan tan A B C +=-,这是常用的结论,另外利用正弦定理或余弦定理处理条件中含有边或角的等式,常考虑对其实施“边化角”或“角化边”.6． （2017新课标全国Ⅰ理科）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，已知ABC△的面积为23sin a A. （1）求sin B sin C ;（2）若6cos B cos C =1，a =3，求ABC △的周长.【答案】（1）23；（2）3+【解析】（1）由题设得21sin 23sin a ac B A =，即1sin 23sin ac B A=.由正弦定理得1sin sin sin 23sin AC B A =. 故2sin sin 3B C =.【名师点睛】在处理解三角形问题时，要注意抓住题目所给的条件，当题设中给定三角形的面积，可以使用面积公式建立等式，再将所有边的关系转化为角的关系，有时需将角的关系转化为边的关系；解三角形问题常见的一种考题是“已知一条边的长度和它所对的角，求面积或周长的取值范围”或者“已知一条边的长度和它所对的角，再有另外一个条件，求面积或周长的值”，这类问题的通法思路是：全部转化为角的关系，建立函数关系式，如sin()y A x b ωϕ=++，从而求出范围，或利用余弦定理以及基本不等式求范围；求具体的值直接利用余弦定理和给定条件即可.。

训练　三角恒等变换与解三角形 一、选择题(每小题5分，共25分) 1．已知α，β都是锐角，若sin α＝，sin β＝，则α＋β＝( )． A. B. C.和 D．－和－ 2．已知sin α－cos α＝，α(0，π)，则tan α＝( )． A．－1 B．－ C. D．1 3．在ABC中，a＝4，b＝，5cos(B＋C)＋3＝0，则角B的大小为( )． A. B. C. D.π 4．ABC中，角A、B、C所对的边分别为a、b、c，若＜cos A，则ABC为( )． A．钝角三角形 B．直角三角形 C．锐角三角形 D．等边三角形 5．若ABC的内角A，B，C所对的边a，b，c满足(a＋b)2－c2＝4，且C＝60°，则a＋b的最小值为( )． A. . C. D. 二、填空题(每小题5分，共15分) 6．在ABC中，三个内角A，B，C的对边分别为a，b，c，若b＝2，B＝，sin C＝，则c＝________；a＝________.7．在ABC中，sin2C＝sin Asin B＋sin2B，a＝2b，则角C＝________. 8．在ABC中，角A，B，C的对边分别为a，b，c，已知4sin2－cos 2C＝，且a＋b＝5，c＝，则ABC的面积为________．三、解答题(本题共3小题，共35分) 9．(11分)已知函数f(x)＝2sin， xR. (1)求f的值； (2)设α，β，f＝，f(3β＋2π)＝，求cos(α＋β)的值． 10．(12分)在ABC中，a，b，c分别是角A，B，C的对边，且2sin2－cos 2A＝. (1)求角A的度数； (2)若a＝，b＋c＝3(b＞c)，求b和c的值． 11．(12分)如图，某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度：在C处进行该仪器的垂直弹射，观测点A、B两地相距100米，BAC＝60°，在A地听到弹射声音的时间比B地晚秒．A地测得该仪器在C处时的俯角为15°，A地测得最高点H的仰角为30°，求该仪器的垂直弹射高度CH.(声音的传播速度为340米/秒)1．A　[因为α、β都为锐角，所以cos α＝＝，cos β＝＝.所以cos(α＋β)＝cos α·cos β－sin α·sin β＝，所以α＋β＝，故选A.] 2．A　[利用辅助角公式求出α，再求其正切值．由sin α－cosα＝sin＝，α(0，π)，解得α＝，所以tanα＝tan＝－1.] 3．A　[由5 cos(B＋C)＋3＝0，得cos A＝，则sin A＝， ＝，sin B＝.又a＞b，B必为锐角，所以B＝.] 4．A　[依题意，得＜cos A，sin C＜sin Bcos A，所以sin(A＋B)＜sin Bcos A，即sin Bcos A＋cos BsinA－sin Bcos A＜0，所以cos Bsin A＜0.又sin A＞0，于是有cos B＜0，B为钝角，ABC是钝角三角形，选A.] 5．D　[由余弦定理可得：c2＝a2＋b2－2abcos C＝a2＋b2－ab＝(a＋b)2－3ab＝(a＋b)2－4，所以有ab＝≤2，解得a＋b≥.] 6．解析　利用正弦定理可知：c＝＝2，b2＝a2＋c2－2accos B，a2－4a－12＝0，a＝6. 答案：2　6 7．解析　由正弦定理知，c2＝ab＋b2，所以cos C＝＝＝＝＝，所以C＝. 答案 8．解析　因为4sin2－cos 2C＝， 所以2[1－cos(A＋B)]－2cos2C＋1＝， 2＋2cos C－2cos2C＋1＝， cos2C－cos C＋＝0，解得cos C＝. 根据余弦定理有cos C＝＝，ab＝a2＋b2－7， 3ab＝a2＋b2＋2ab－7＝(a＋b)2－7＝25－7＝18， ab＝6. 所以S＝absin C＝×6×＝. 答案 9．解　(1)由题设知：f＝2sin＝2sin＝. (2)由题设知：＝f＝2sin α， ＝f(3β＋2π)＝2sin＝2cos β， 即sin α＝，cos β＝.又α，β，cos α＝，sin β＝，cos(α＋β)＝cos αcos β－sin αsinβ＝×－×＝. 10．解 (1)由2sin2－cos 2A＝及A＋B＋C＝180°， 得2[1－cos (B＋C)]－2cos2A＋1＝， 4(1＋cos A)－4cos2A＝5. 4cos2A－4cos A＋1＝0.cos A＝. ∵0°＜A＜180°，A＝60°. (2)由余弦定理，得cos A＝.∵cos A＝，＝.∴(b＋c)2－a2＝3bc.将a＝，b＋c＝3代入上式得bc＝2. 由及b＞c，得 11．解　由题意，设|AC|＝x，则|BC|＝x－×340＝x－40， 在ABC内，由余弦定理：|BC|2＝|BA|2＋|CA|2－2|BA|·|CA|·cosBAC，即(x－40)2＝x2＋10 000－100x，解得x＝420. 在ACH中，|AC|＝420，CAH＝30°＋15°＝45°，CHA＝90°－30°＝60°，由正弦定理：＝，可得|CH|＝|AC|·＝140. 答：该仪器的垂直弹射高度CH为140米．。

第2讲三角恒等变换与解三角形（文理)JIE TI CE LUE MING FANG XIANG解题策略·明方向⊙︱考情分析︱1．三角恒等变换是高考的热点内容，主要考查利用各种三角函数公式进行求值与化简,其中二倍角公式、辅助角公式是考查的重点，切化弦、角的变换是常考的内容．2．正弦定理、余弦定理以及解三角形问题是高考的必考内容，主要考查：(1）边、角、面积的计算;（2）有关边、角的范围问题；(3)实际应用问题．⊙︱真题分布︱（理科)年份卷别题号考查角度分值202 0Ⅰ卷9、16三角恒等变换和同角间的三角函数关系求值；利用余弦定理解三角形10Ⅱ卷17解三角形求角和周长的12（文科）KAO DIAN FEN LEI XI ZHONG DIAN考点分类·析重点考点一三角恒等变换错误!错误!错误!错误!三角恒等变换与求值1．两角和与差的正弦、余弦、正切公式(1）sin(α±β)＝sin αcos β±cos αsin β。

(2）cos(α±β）＝cos αcos β∓sin αsin β。

(3)tan(α±β)＝错误!。

2．二倍角的正弦、余弦、正切公式(1)sin 2α＝2sin αcos α。

（2)cos 2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α.（3）tan 2α＝错误!.3．辅助角公式a sin x＋b cos x＝错误!sin(x＋φ）（其中tan φ＝错误!)典错误!错误!错误!典例1（1)（2020·全国Ⅱ卷模拟）cos2 40°＋2sin 35°sin 55°sin 10°＝（A)A．错误!B．错误!C．错误!＋错误!D．错误!(2)(2020·宜宾模拟）已知α∈错误!,且3sin2α－5cos2α＋sin 2α＝0，则sin 2α＋cos 2α＝（A)A．1B．－错误!C．－错误!或1D．－1（3）已知函数f（x）＝错误!cos x cos错误!＋sin2错误!－错误!.①求f（x)的单调递增区间;②若x∈错误!，f（x)＝错误!,求cos 2x的值．【解析】（1）原式＝cos240°＋2sin 35°cos 35°sin 10°＝cos240°＋sin 70°sin 10°＝12＋12cos 80°＋sin 70°sin 10°＝错误!＋错误!(cos 70°cos 10°－sin 70°sin 10°＋2sin 70°sin 10°）＝错误!＋错误!(cos 70°cos 10°＋sin 70°sin 10°）＝错误!＋错误!cos 60°＝34。

高三数学三角函数三角恒等变换解三角形试题答案及解析1.已知函数的图象上关于轴对称的点至少有3对，则实数的取值范围是（）A．B．C．D．【答案】A【解析】原函数在轴左侧是一段正弦型函数图象，在轴右侧是一条对数函数的图象，要使得图象上关于轴对称的点至少有对，可将左侧的图象对称到轴右侧，即，应该与原来轴右侧的图象至少有个公共点如图，不能满足条件，只有此时，只需在时，的纵坐标大于，即，得．【考点】分段函数，函数图象，正弦型函数，对数函数2.若，则函数的最大值是___________．【答案】【解析】由题意因为，所以，所以函数的最大值是．【考点】求最大值．3.已知，，则下列不等式一定成立的是A．B．C．D．【答案】D【解析】,【考点】三角函数的性质4.若，且为第二象限角，则（）A．B．C．D．【答案】B【解析】由得又为第二象限角，所以，选B．【考点】两角差余弦公式5.设函数对任意的，都有，若函数，则的值是（）A．1B．-5或3C．-2D．【答案】C【解析】根据题意有是函数图像的对称轴，从而有，所以有，故选C．【考点】三角函数的性质．6.设的最小值为，则．【答案】【解析】，根据题意，结合二次函数在某个区间上的最值问题，对参数进行讨论，当时，其最小值为，所以不合题意，当时，其最小值为，解得，当时，其最小值为，无解，所以．【考点】倍角公式，二次函数在给定区间上的最值问题．7.设函数对任意的，都有，若函数，则的值是（）A．1B．-5或3C．D．-2【答案】D【解析】根据题意有是函数图像的对称轴，从而有，所以有，故选D．【考点】三角函数的性质．8.下列函数中，以为最小正周期的偶函数是（）A．y=sin2x+cos2xB．y=sin2xcos2xC．y=cos（4x+）D．y=sin22x﹣cos22x【答案】D【解析】因为A项为非奇非偶函数，B项是奇函数，C项是奇函数，只有D项是符合题意的，故选D．【考点】诱导公式，倍角公式，三角函数的奇偶性和周期．9.函数的最大值为．【答案】【解析】解析式表示过的直线的斜率，由几何意义，即过定点（4，3）与单位圆相切时的切线斜率为最值．所以设切线得斜率为k，则直线方程为，即 ,【考点】三角函数最值【方法点睛】本题主要考查三角函数最值问题及转化的思想，解决问题的根据是根据所给函数式子转化为直线与圆的位置关系问题，即将所给式子看做定点与单位圆上点的连线的斜率的范围问题，通过模型转化使问题定点巧妙解决，属于经典试题．10.（本题满分12分）如图，在中，边上的中线长为3，且，．（1）求的值；（2）求边的长．【答案】（1）（2）4【解析】（1）利用角的关系，再结合两角差正弦公式展开就可求解（2）先在三角形ABD中，由正弦定理解出BD长，即CD长：由正弦定理，得，即，解得…故；再在三角形ADC中由余弦定理解出AC：；AC= 4试题解析：（1）（2）在中，由正弦定理，得，即，解得…故，从而在中，由余弦定理，得；AC= 4 ；【考点】正余弦定理11.中，，则的最大值为．【答案】【解析】设，由余弦定理的推论，所以，设，代入上式得，，故，当时，此时，符合题意，因此最大值为，故答案为：．【考点】解三角形．【思路点睛】首先假设，然后再根据余弦定理的推论，可得，找到与的关系，再设，代入上式得，利用根的判别式，进而求出结果．本题的关键是利用余弦定理的推论．12.已知函数的部分图象如图所示．（1）求函数的解析式；（2）若，求函数在区间上的单调减区间．【答案】（1）；（2），．【解析】（1）由图象中的最高点和最低点的纵坐标得到关于的方程组求得，再利用图象得到函数的周期，进而得到值，最后代入最低点坐标或最高点坐标结合的范围求出，即得到函数的解析式；（2）先求出，利用两角和差的正弦公式将其化为的形式，再利用整体思想求其单调递减区间．试题解析：（1）由图知，解得，又，所以，所以，将点代入，得，再由，得，所以；（2）因为由，解得；又，故所求的单调减区间为，．【考点】1.三角函数的图象与性质；2.三角恒等变形．13.已知角的终边经过点（-4，3），则= ，= ；【答案】;【解析】由题意可得.【考点】任意角三角函数的定义.14.在△ABC中，a、b、c分别是角A、B、C的对边，且．（Ⅰ）求角B的大小；（Ⅱ）若，求△ABC的面积．【答案】（Ⅰ）；（Ⅱ）．【解析】（Ⅰ）在解三角形的背景下，考查正弦定理，余弦定理，知值求值．（Ⅱ）综合余弦定理，求三角形的面积公式，需要把作为整体求之．试题解析：（Ⅰ）由正弦定理得将上式代入已知即，即．∵∵∵B为三角形的内角，∴．（Ⅱ）由余弦定理得，结合，可得，所以△ABC的面积．【考点】正弦定理，余弦定理，三角形的面积公式．15.在△中，角，，所对的边分别为，，，表示△的面积，若，，则．【答案】【解析】∵，∴，∴，∴，．∵，∴，∴，∴，∴．【考点】解三角形．【思路点睛】先利用余弦定理和三角形的面积公式可得，可得，再用正弦定理把中的边换成角的正弦，利用两角和公式化简整理可求得，最后根据三角形内角和，进而求得．16.中，角A，B，C的对边分别为a，b，c，若的面积，则 .【答案】【解析】由余弦定理，，又，，，即，，．【考点】1、余弦定理；2、同角三角函数的基本关系；3、三角形面积公式.【思路点睛】本题主要考查的是余弦定理、同角三角函数基本关系、三角形的面积公式，属于容易题.因为题目求，且的面积，边的平方的形式一般想到余弦定理，面积展开后利用余弦定理即可求得与的关系，从而利用同角三角函数的基本关系求得.17.（2012•安徽）设△ABC的内角A、B、C所对边的长分别为a、b、c，且有2sinBcosA=sinAcosC+cosAsinC．（Ⅰ）求角A的大小；（Ⅱ）若b=2，c=1，D为BC的中点，求AD的长．【答案】（Ⅰ）；（Ⅱ）【解析】（Ⅰ）根据2sinBcosA=sinAcosC+cosAsinC，可得2sinBcosA=sin（A+C），从而可得2sinBcosA=sinB，由此可求求角A的大小；（Ⅱ）利用b=2，c=1，A=，可求a的值，进而可求B=，利用D为BC的中点，可求AD的长．解：（Ⅰ）∵2sinBcosA=sinAcosC+cosAsinC∴2sinBcosA=sin（A+C）∵A+C=π﹣B∴sin（A+C）=sinB＞0∴2sinBcosA=sinB∴cosA=∵A∈（0，π）∴A=；（Ⅱ）∵b=2，c=1，A=∴a2=b2+c2﹣2bccosA=3∴b2=a2+c2∴B=∵D为BC的中点，∴AD=．【考点】余弦定理；三角函数的恒等变换及化简求值．18.在中，已知．（Ⅰ）求sinA与角B的值；（Ⅱ）若角A,B,C的对边分别为的值．【答案】（Ⅰ）；（Ⅱ），．【解析】（I）给出了关于角的两个三角函数值，利用诱导公式和同角三角函数的基本关系式可求得其正弦、余弦，再根据三角形的性质可求得的值；（II）在第一问的基础上，利用正弦定理可求得边，再由余弦定理求边，注意利用三角形基本性质舍解．试题解析：（Ⅰ）∵，，又∵，．∵，且，．（Ⅱ）由正弦定理得，，另由得，解得或（舍去），，．【考点】三角函数的诱导公式，同角三角函数的基本关系式及利用正、余弦定理在解三角形．19.已知，则的值为．【答案】．【解析】，故填：．【考点】三角恒等变形．20.在中，角A，B，C的对边分别为，，，若，则角的值为（）A．或B．或C．D．【答案】A．【解析】，，∴或，故选A．【考点】余弦定理．【思路点睛】由已知条件，可先将切化弦，再结合正弦定理，将该恒等式的边都化为角，然后进行三角函数式的恒等变形，找出角之间的关系；或将角都化成边，然后进行代数恒等变形，可一题多解，多角度思考问题，从而达到对知识的熟练掌握．21.为了得到函数的图象，只需把函数图象上的所有点（）A．横坐标缩短到原来的倍，纵坐标不变B．横坐标伸长到原来的2倍，纵坐标不变C．纵坐标缩短到原来的倍，横坐标不变D．纵坐标缩短到原来的2倍，横坐标不变【答案】A【解析】这是一个三角函数的图象变换问题，一般的为了得到函数的图象，只需把函数的图象上所有点的横坐标伸长（）或缩短（）到原来的倍（纵坐标不变）即可，因此为了得到函数的图象，只需把函数图象上的所有点横坐标缩短到原来的倍，纵坐标不变，故选A.【考点】三角函数的图象变换．【方法点睛】本题是一个三角函数的图象变换问题，属于容易题.一般的要得到函数（其中）的图像可按以下步骤进行：先把的图象向左（）或向右（）平移个单位，再将所得函数的图象上各点的横坐标扩大（）或缩小（）为原来的（纵坐标不变），再把所得函数图象上各点的纵坐标扩大（）或缩小（）为原来的倍（横坐标不变），最后再将所得图像向上（）或向下（）平移个单位，即可得到函数的图象.22.如图，在中，，，点在边上，且，.（I）求；（II）求的长.【答案】（Ⅰ）；（Ⅱ），.【解析】（Ⅰ）由图可知，所以，又，所以，再由两角差的正弦公式可求得；（Ⅱ）由题意可用正弦定理、余弦定理即可求出、的长，在中，有，又从而可求得；在中，由余弦定理得，，从而可求出.试题解析：（Ⅰ）在中，因为，所以，所以（Ⅱ）在中，由正弦定理得，在中，由余弦定理得，所以【考点】1.解三角形；2.两角差的正弦公式.23.设的内角对边分别为，已知，且.（1）求角的大小；（2）若向量与共线，求的值.【答案】(1);(2)。

第2讲 三角恒等变换与解三角形[做真题]题型一 三角恒等变换1．(·高考全国卷Ⅱ)已知α∈⎝⎛⎭⎫0，π2，2sin 2α＝cos 2α＋1，则sin α＝( ) A ．15B ．55C ．33D ．255解析：选B.由2sin 2α＝cos 2α＋1，得4sin αcos α＝1－2 sin 2α＋1，即2sin αcos α＝1－sin 2α.因为α∈⎝⎛⎭⎫0，π2，所以cos α＝1－sin 2α，所以2sin α1－sin 2α＝1－sin 2 α，解得sin α＝55，故选B.2．(·高考全国卷Ⅲ)若sin α＝13，则cos 2α＝( )A ．89B ．79C ．－79D ．－89解析：选B.cos 2α＝1－2sin 2α＝1－2×⎝⎛⎭⎫132＝79. 3．(·高考全国卷Ⅱ)若cos ⎝⎛⎭⎫π4－α＝35，则sin 2α＝( ) A ．725B ．15C ．－15D ．－725解析：选D.因为cos ⎝⎛⎭⎫π4－α＝cos π4cos α＋sin π4sin α＝22(sin α＋cos α)＝35，所以sin α＋cos α＝325，所以1＋sin 2α＝1825，所以sin 2α＝－725，故选D.题型二 三角形中的边角计算问题1．(·高考全国卷Ⅱ)在△ABC 中，cos C 2＝55，BC ＝1，AC ＝5，则AB ＝( )A ．4 2B ．30C ．29D ．2 5解析：选A.因为cos C 2＝55，所以cos C ＝2cos 2C 2－1＝2×⎝⎛⎭⎫552－1＝－35.于是，在△ABC中，由余弦定理得AB 2＝AC 2＋BC 2－2AC ·BC ·cos C ＝52＋12－2×5×1×⎝⎛⎭⎫－35＝32，所以AB ＝4 2.故选A.2．(·高考山东卷)△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，已知b ＝c ，a 2＝2b 2(1－sin A )，则A ＝( )A ．3π4B ．π3C ．π4D ．π6解析：选C.由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝2b 2－2b 2cos A ，所以2b 2(1－sin A )＝2b 2(1－cos A )，所以sin A ＝cos A ，即tan A ＝1，又0<A <π，所以A ＝π4.3．(·高考全国卷Ⅰ)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，设(sin B －sin C )2＝sin 2A －sin B sin C .(1)求A ；(2)若2a ＋b ＝2c ，求sin C .解：(1)由已知得sin 2B ＋sin 2C －sin 2A ＝sin B sin C ，故由正弦定理得b 2＋c 2－a 2＝bc . 由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝12.因为0°＜A ＜180°， 所以A ＝60°.(2)由(1)知B ＝120°－C ，由题设及正弦定理得2sin A ＋sin(120°－C )＝2sin C ，即62＋32cos C ＋12sin C ＝2sin C ，可得cos(C ＋60°)＝－22.由于0°＜C ＜120°，所以sin(C ＋60°)＝22，故 sin C ＝sin(C ＋60°－60°)＝sin(C ＋60°)cos 60°－cos(C ＋60°)sin 60° ＝6＋24. 题型三 与三角形面积有关的问题1．(·高考全国卷Ⅲ)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .若△ABC 的面积为a 2＋b 2－c 24，则C ＝( ) A ．π2B ．π3C ．π4D ．π6解析：选C.根据题意及三角形的面积公式知12ab sin C ＝a 2＋b 2－c 24，所以sin C ＝a 2＋b 2－c 22ab ＝cos C ，所以在△ABC 中，C ＝π4.2．(·高考全国卷Ⅱ)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .若b ＝6，a ＝2c ，B ＝π3，则△ABC 的面积为________．解析：法一：因为a ＝2c ，b ＝6，B ＝π3，所以由余弦定理b 2＝a 2＋c 2－2ac cos B ，得62＝(2c )2＋c 2－2×2c ×c cos π3，得c ＝23，所以a ＝43，所以△ABC 的面积S ＝12ac sin B ＝12×43×23×sin π3＝6 3.法二：因为a ＝2c ，b ＝6，B ＝π3，所以由余弦定理b 2＝a 2＋c 2－2ac cos B ，得62＝(2c )2＋c 2－2×2c ×c cos π3，得c ＝23，所以a ＝43，所以a 2＝b 2＋c 2，所以A ＝π2，所以△ABC 的面积S ＝12×23×6＝6 3.答案：6 33．(·高考全国卷Ⅲ)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知a sinA ＋C2＝b sin A .(1)求B ；(2)若△ABC 为锐角三角形，且c ＝1，求△ABC 面积的取值范围． 解：(1)由题设及正弦定理得 sin A sinA ＋C2＝sin B sin A . 因为sin A ≠0，所以sin A ＋C2＝sin B .由A ＋B ＋C ＝180°，可得sin A ＋C 2＝cos B 2，故cos B 2＝2sin B 2cos B2.因为cos B 2≠0，故sin B 2＝12，因此B ＝60°.(2)由题设及(1)知△ABC 的面积S △ABC ＝34a . 由正弦定理得a ＝c sin A sin C ＝sin （120°－C ）sin C ＝32tan C ＋12.由于△ABC 为锐角三角形，故0°<A <90°，0°<C <90°. 由(1)知A ＋C ＝120°，所以30°<C <90°，故12<a <2，从而38<S △ABC <32.因此，△ABC 面积的取值范围是⎝⎛⎭⎫38，32. [山东省学习指导意见]1．三角恒等变换(1)会利用向量推导出两角差的余弦公式，并能从两角差的余弦公式导出两角和与差的正弦、余弦、正切公式，二倍角的正弦、余弦、正切公式，了解它们的内在联系．(2)能运用上述公式进行简单的恒等变换． 2．解三角形(1)通过对任意三角形边长和角度关系的探索，掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题．(2)能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题．三角恒等变换与求值[考法全练]1．(·高考全国卷Ⅰ)tan 255°＝()A．－2－3B．－2＋ 3C．2－ 3 D．2＋ 3解析：选D.由正切函数的周期性可知，tan 255°＝tan(180°＋75°)＝tan 75°＝tan(30°＋45°)＝33＋11－33＝2＋3，故选D.2．(一题多解)(·福建五校第二次联考)已知cos⎝⎛⎭⎫π4－α＝45，则sin 2α＝() A．15B．－15C ．725D ．－725解析：选C.法一：因为cos ⎝⎛⎭⎫π4－α＝45，所以sin 2α＝sin ⎣⎡⎦⎤π2－2⎝⎛⎭⎫π4－α＝cos 2⎝⎛⎭⎫π4－α＝2cos 2⎝⎛⎭⎫π4－α－1＝2×⎝⎛⎭⎫452－1＝725.故选C. 法二：令π4－α＝θ，则α＝π4－θ，cos θ＝45，所以sin 2α＝sin 2⎝⎛⎭⎫π4－θ＝sin ⎝⎛⎭⎫π2－2θ＝cos 2θ＝2cos 2θ－1＝2×⎝⎛⎭⎫452－1＝725.故选C.法三：因为cos ⎝⎛⎭⎫π4－α＝45，所以22(cos α＋sin α)＝45，所以cos α＋sin α＝425，平方得1＋sin 2α＝3225，得sin 2α＝725.故选C.3．(·山东高考模拟)已知cos ⎝⎛⎭⎫α＋π6－sin α＝435，则sin ⎝⎛⎭⎫α＋11π6＝________．解析：根据题意得cos ⎝ ⎛⎭⎪⎫α＋π6－sin α＝32cos α－32sin α＝435，所以sin ⎝ ⎛⎭⎪⎫α－π6＝－45，所以sin ⎝ ⎛⎭⎪⎫α＋11π6＝sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α－π6＋2π＝sin ⎝⎛⎭⎪⎫α－π6＝－45.答案：－454．(·贵州黔东南一模改编)已知sin α＋3cos α＝－10，则tan 2α＝________，tan ⎝⎛⎭⎫α＋π4＝________．解析：因为(sin α＋3cos α)2＝sin 2α＋6sin αcos α＋9cos 2α＝10(sin 2α＋cos 2α)，所以9sin 2α－6sin αcos α＋cos 2α＝0，则(3tan α－1)2＝0，即tan α＝13，所以tan 2α＝2tan α1－tan 2α＝34，tan ⎝⎛⎭⎫α＋π4＝13＋11－13＝2. 答案：342三角恒等变换要遵循的“三看”原则一看“角”，通过看角之间的差别与联系，把角进行合理的拆分；二看“函数名称”，是需进行“切化弦”还是“弦化切”等，从而确定使用的公式；三看“结构特征”，了解变式或化简的方向．三角形的基本量的计算[典型例题]命题角度一求解三角形中的角(1)(·江西七校第一次联考)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知b ＝a (cos C ＋33sin C )，a ＝2，c ＝263，则角C ＝( ) A ．3π4B ．π3C ．π6D ．π4(2)已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且b cos C ＋b sin C ＝a . ①求角B 的大小；②若BC 边上的高等于14a ，求cos A 的值．【解】 (1)选D.由b ＝a ⎝⎛⎭⎫cos C ＋33sin C ， 得sin B ＝sin A ⎝⎛⎭⎫cos C ＋33sin C .因为sin B ＝sin []π－（A ＋C ）＝sin(A ＋C )， 所以sin A cos C ＋cos A sin C ＝sin A cos C ＋33sin A sin C (sin C ≠0)，即cos A ＝33sin A ，所以tan A ＝ 3.因为0<A <π，所以A ＝π3.由正弦定理a sin A ＝c sin C ，得sin C ＝22.因为0<C <2π3，所以C ＝π4.故选D.(2)①由b cos C ＋b sin C ＝a ， 得sin B cos C ＋sin B sin C ＝sin A . 因为A ＋B ＋C ＝π，所以sin B cos C ＋sin B sin C ＝sin(B ＋C )，即sin B cos C ＋sin B sin C ＝sin B cos C ＋cos B sin C ， 因为sin C ≠0，所以sin B ＝cos B . 因为B ∈(0，π)，所以B ＝π4.②设BC 边上的高为AD ，则AD ＝14a .因为B ＝π4，所以BD ＝AD ＝14a ，所以CD ＝34a ，所以AC ＝AD 2＋DC 2＝104a ，AB ＝24a . 由余弦定理得cos A ＝AB 2＋AC 2－BC 22AB ·AC ＝－55.利用正、余弦定理求三角形角的方法(1)已知两边及其夹角，先由余弦定理求第三边，再由正弦定理求角． (2)已知三边，直接由余弦定理求角．(3)已知两边及其中一边的对角，先由正弦定理求另一边的对角，再由三角形内角和求第三角．[技能] 利用正、余弦定理求角时的两个失分点：(1)已知两边及其中一边的对角求其他角时，有一解、两解的情况，容易把握不准而出错；(2)在变形时，直接两边约去公因式，没有移项后提公因式，产生漏解．命题角度二 求解三角形中的边与面积如图所示，在△ABC 中，点D 为BC 边上一点，且BD ＝1，E 为AC 的中点，AE ＝32，cos B ＝277，∠ADB＝2π3. (1)求AD 的长； (2)求△ADE 的面积．【解】 (1)在△ABD 中，因为cos B ＝277，B ∈(0，π)，所以sin B ＝1－cos 2B ＝1－⎝⎛⎭⎫2772＝217， 所以sin ∠BAD ＝sin(B ＋∠ADB )＝217×⎝⎛⎭⎫－12＋277×32＝2114. 由正弦定理知AD sin B ＝BD sin ∠BAD ，得AD ＝BD ·sin Bsin ∠BAD＝1×2172114＝2. (2)由(1)知AD ＝2，依题意得AC ＝2AE ＝3，在△ACD 中，由余弦定理得AC 2＝AD 2＋DC 2－2AD ·DC cos ∠ADC ，即9＝4＋DC 2－2×2×DC cos π3，所以DC 2－2DC －5＝0，解得DC ＝1＋6(负值舍去)，所以S △ACD ＝12AD ·DC sin ∠ADC ＝12×2×(1＋6)×32＝3＋322，从而S △ADE ＝12S △ACD ＝3＋324.利用余弦定理求边，一般是已知三角形的两边及其夹角．利用正弦定理求边，必须知道两角及其中一边，如该边为其中一角的对边，要注意解的多样性与合理性．而三角形的面积主要是利用两边与其夹角的正弦值求解．[技能] 三角形的面积主要是利用S ＝12ab sin C 求解，有时可以直接利用余弦定理求出ab的整体值再求面积，而不必分别求出a ，b 的值．[对点训练]1．(水浒原创)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c . (1)从下列两个条件中任选一个作条件，求角B ； ①a ＝b cos C ＋12c ，②a 2＋c 2－b 2＝ab cos A ＋a 2cos B .(2)利用(1)的结果，若b ＝27，tan C ＝32，求△ABC 的面积． 解：(1)若选①，由a ＝b cos C ＋12c 及正弦定理，得sin A ＝sin B cos C ＋12sin C ，又sin A ＝sin(B ＋C )＝sin B cos C ＋cos B sin C ，所以cos B sin C ＝12sin C ．又在△ABC 中，sin C ≠0，所以cos B ＝12，B ＝π3.若选②，因为a 2＋c 2－b 2＝ab cos A ＋a 2cos B ，所以由余弦定理，得2ac cos B ＝ab cos A ＋a 2cos B ，又a ≠0，所以2c cos B ＝b cos A ＋a cos B ，由正弦定理，得2sin C cos B ＝sin B cos A ＋sin A cos B ＝sin(A ＋B )＝sin C ，又C ∈(0，π)，sin C >0，所以cos B ＝12.因为B ∈(0，π)，所以B ＝π3.(2)由tan C ＝32，C ∈(0，π)，得sin C ＝217，cos C ＝277， 所以sin A ＝sin(B ＋C )＝sin B cos C ＋cos B sin C ＝32×277＋12×217＝32114. 由正弦定理a sin A ＝b sin B ，得a ＝b sin Asin B＝27×3211432＝6， 所以△ABC 的面积为12ab sin C ＝12×6×27×217＝6 3.2．(·郑州市第一次质量预测)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 的面积为S ，且满足sin B ＝b 24S.(1)求sin A sin C ；(2)若4cos A cos C ＝3，b ＝15，求△ABC 的周长． 解：(1)由三角形的面积公式可得S ＝12bc sin A ，又sin B ＝b 24S，所以2bc sin A sin B ＝b 2，即2c sin A sin B ＝b ，由正弦定理可得2sin C sin A sin B ＝sin B ， 因为sin B ≠0，所以sin A sin C ＝12.(2)因为4cos A cos C ＝3，所以cos A cos C ＝34，所以cos A cos C －sin A sin C ＝34－12＝14，即cos(A ＋C )＝14，所以cos B ＝－14，因为0<B <π，所以sin B ＝154，因为a sin A ＝b sin B ＝c sin C ＝15154＝4，所以sin A sin C ＝ac 16＝12，所以ac ＝8，因为b 2＝a 2＋c 2－2ac cos B ＝(a ＋c )2－2ac －2ac cos B ， 所以(a ＋c )2＝15＋12＝27， 所以a ＋c ＝3 3.所以△ABC 的周长为a ＋b ＋c ＝33＋15.解三角形的综合问题[典型例题]命题角度一 以平面几何为载体的解三角形问题(·洛阳尖子生第二次联考)如图，在平面四边形ABCD 中，∠ABC 为锐角，AD ⊥BD ，AC 平分∠BAD ，BC ＝23，BD ＝3＋6，△BCD 的面积S ＝3（2＋3）2.(1)求CD ； (2)求∠ABC .【解】 (1)在△BCD 中，S ＝12BD ·BC ·sin ∠CBD ＝3（2＋3）2，因为BC ＝23，BD ＝3＋6， 所以sin ∠CBD ＝12.因为∠ABC 为锐角，所以∠CBD ＝30°.在△BCD 中，由余弦定理得CD 2＝BC 2＋BD 2－2BC ·BD ·cos ∠CBD ＝(23)2＋(3＋6)2－2×23×(3＋6)×32＝9，所以CD ＝3. (2)在△BCD 中，由正弦定理得BC sin ∠BDC ＝CDsin ∠CBD ，即23sin ∠BDC ＝3sin 30°，解得sin ∠BDC ＝33.因为BC <BD ，所以∠BDC 为锐角，所以cos ∠BDC ＝63. 在△ACD 中，由正弦定理得AC sin ∠ADC ＝CDsin ∠CAD，即AC cos ∠BDC ＝3sin ∠CAD.①在△ABC 中，由正弦定理得AC sin ∠ABC ＝BCsin ∠BAC，即AC sin ∠ABC ＝23sin ∠BAC.②因为AC 平分∠BAD ，所以∠CAD ＝∠BAC . 由①②得sin ∠ABCcos ∠BDC ＝323，解得sin ∠ABC ＝22.因为∠ABC 为锐角，所以∠ABC ＝45°.解决以平面几何为载体的问题，主要注意以下几方面：一是充分利用平面几何图形的性质；二是出现多个三角形时，从条件较多的三角形突破求解；三是四边形问题要转化到三角形中去求解；四是通过三角形中的不等关系(如大边对大角，最大角一定大于等于π3)确定角或边的范围．命题角度二 三角形中的最值或范围问题(1)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，外接圆的半径为1，且tan A tan B ＝2c －bb，则△ABC 面积的最大值为________．(2)已知△ABC 的内角A ，B ，C 的对边分别是a ，b ，c ，且(a 2＋b 2－c 2)(a cos B ＋b cos A )＝abc ，则c ＝________．若a ＋b ＝2，则c 的取值范围为________．【解析】 (1)因为tan A tan B ＝2c －b b ，所以b sin A cos A ＝(2c －b )sin Bcos B ，由正弦定理得sin B sin A cos B＝(2sin C －sin B )sin B cos A ，又sin B ≠0，所以sin A cos B ＝(2sin C －sin B )cos A ，所以sin A cos B ＋sin B cos A ＝2sin C cos A ，即sin(A ＋B )＝2sin C cos A ，即sin C ＝2sin C cos A ，又sin C ≠0，所以cos A ＝12，sin A ＝32.设外接圆的半径为r ，则r ＝1，由余弦定理得bc ＝b 2＋c 2－a 22cos A ＝b 2＋c 2－a 2＝b 2＋c 2－(2r sin A )2＝b 2＋c 2－3≥2bc －3(当且仅当b ＝c 时，等号成立)，所以bc ≤3，所以S △ABC ＝12bc sin A ＝34bc ≤334.所以△ABC 面积的最大值为334.(2)由sin A cos B ＋sin B cos A ＝sin(A ＋B )＝sin C 及正弦定理，可知a cos B ＋b cos A ＝c ，则由(a 2＋b 2－c 2)(a cos B ＋b cos A )＝abc ，得a 2＋b 2－c 2＝ab ，由余弦定理可得cos C ＝12，则C ＝π3，B ＝2π3－A ，由正弦定理a sin A ＝b sin B ＝c sin C ，得a sin A＝b sin ⎝⎛⎭⎫2π3－A ＝c sin π3，又a ＋b ＝2，所以c sin A32＋c sin ⎝⎛⎭⎫2π3－A 32＝2，即c ＝3sin A ＋sin ⎝⎛⎭⎫2π3－A ＝1sin ⎝⎛⎭⎫A ＋π6，因为A ∈⎝⎛⎭⎫0，2π3，所以A ＋π6∈⎝⎛⎭⎫π6，5π6，sin ⎝⎛⎭⎫A ＋π6∈⎝⎛⎦⎤12，1，则c ∈[1，2)． 【答案】 (1)334 (2)π3[1，2)解三角形中的最值与范围问题主要有两种解决方法：一是利用基本不等式求得最大值或最小值；二是将所求式转化为只含有三角形某一个角的三角函数形式，结合角的范围确定所求式的范围．[对点训练]1.(·重庆市七校联合考试)如图，在平面四边形ABCD 中，E 为AB 边上一点，连接CE ，DE .CB ＝2，BE ＝1，∠B ＝∠CED ＝2π3.(1)求sin ∠AED 的值； (2)若AB ∥CD ，求CD 的长．解：(1)在△BEC 中，由余弦定理得，CE ＝CB 2＋BE 2－2CB ·BE cos ∠B ＝7，又BEsin ∠BCE＝CE sin ∠B，所以sin ∠BCE ＝2114，因为∠B ＝∠CED ，所以sin ∠AED ＝sin ∠BCE ＝2114. (2)因为AB ∥CD ，所以∠CDE ＝∠AED ， 所以sin ∠CDE ＝sin ∠AED ＝2114，在△CDE 中，CD sin ∠CED ＝CEsin ∠CDE ，所以CD ＝CE sin ∠CED sin ∠CDE＝7×322114＝7. 2．(·福建五校第二次联考)在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，且3a cos C ＝(2b －3c )cos A .(1)求角A 的大小；(2)若a ＝2，求△ABC 面积的最大值．解：(1)由正弦定理可得，3sin A cos C ＝2sin B cos A －3sin C cos A ， 从而3sin(A ＋C )＝2sin B cos A ，即3sin B ＝2sin B cos A . 又B 为三角形的内角，所以sin B ≠0，于是cos A ＝32，又A 为三角形的内角，所以A ＝π6. (2)由余弦定理a 2＝b 2＋c 2－2bc cos A ，得4＝b 2＋c 2－2bc ×32≥2bc －3bc ，所以bc ≤4(2＋3)，所以S △ABC ＝12bc sin A ≤2＋3，故△ABC 面积的最大值为2＋ 3.[A 组 夯基保分专练]一、选择题1．已知sin(α＋π4)＝35，π4<α<3π4，则cos 2α的值为( )A ．－725B ．－7225C ．－2425D ．－1225解析：选C.因为sin(α＋π4)＝35，π4<α<3π4，π2<α＋π4<π，所以cos(α＋π4)<0，可得cos(α＋π4)＝－45，所以sin α＝sin[(α＋π4)－π4]＝sin(α＋π4)cos π4－cos(α＋π4)sin π4＝7210，cos 2α＝1－2sin 2α＝1－4925＝－2425，故选C.2．(·高考全国卷Ⅰ)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知a sin A －b sin B ＝4c sin C ，cos A ＝－14，则bc＝( )A ．6B ．5C ．4D ．3解析：选A.由题意及正弦定理得，b 2－a 2＝－4c 2，所以由余弦定理得，cos A ＝b 2＋c 2－a 22bc ＝－3c 22bc ＝－14，得b c＝6.故选A. 3．在△ABC 中，内角A ，B ，C 的对边分别是a ，b ，c ，若c ＝2a ，b sin B －a sin A ＝12a sinC ，则sin B 为( )A ．74B ．34C ．73D ．13解析：选A.由b sin B －a sin A ＝12a sin C ，且c ＝2a ，得b ＝2a ，因为cos B ＝a 2＋c 2－b 22ac ＝a 2＋4a 2－2a 24a 2＝34，所以sin B ＝1－⎝⎛⎭⎫342＝74.4．(一题多解)在△ABC 中，已知AB ＝2，AC ＝5，tan ∠BAC ＝－3，则BC 边上的高等于( )A ．1B ． 2C ． 3D ．2解析：选A.法一：因为tan ∠BAC ＝－3，所以sin ∠BAC ＝310，cos ∠BAC ＝－110.由余弦定理，得BC 2＝AC 2＋AB 2－2AC ·AB ·cos ∠BAC ＝5＋2－2×5×2×⎝⎛⎭⎫－110＝9，所以BC ＝3，所以S △ABC ＝12AB ·AC ·sin ∠BAC ＝12×2×5×310＝32，所以BC 边上的高h ＝2S △ABC BC ＝2×323＝1，故选A.法二：因为tan ∠BAC ＝－3，所以cos ∠BAC ＝－110<0，则∠BAC 为钝角，因此BC 边上的高小于2，故选A.5.如图，在△ABC 中，∠C ＝π3，BC ＝4，点D 在边AC 上，AD ＝DB ，DE ⊥AB ，E 为垂足．若DE ＝22，则cos A 等于( )A ．223B ．24C ．64D ．63解析：选C.依题意得，BD ＝AD ＝DE sin A ＝22sin A ，∠BDC ＝∠ABD ＋∠A ＝2∠A .在△BCD 中，BC sin ∠BDC ＝BD sin C ，4sin 2A ＝22sin A×23＝423sin A ，即42sin A cos A ＝423sin A ，由此解得cos A ＝64.6．(多选)下列命题中，正确的是( ) A ．在△ABC 中，若A >B ，则sin A >sin BB ．在锐角三角形ABC 中，不等式sin A >cos B 恒成立C ．在△ABC 中，若a cos A －b cos B ＝0，则△ABC 必是等腰直角三角形D ．在△ABC 中，若B ＝60°，b 2＝ac ，则△ABC 必是等边三角形 解析：选ABD.对于A ，在△ABC 中，由正弦定理可得a sin A ＝bsin B，所以sin A >sin B ⇔a >b ⇔A >B ，故A 正确；对于B ，在锐角三角形ABC 中，A ，B ∈⎝⎛⎭⎫0，π2，且A ＋B >π2，则π2>A >π2－B >0，所以sin A >sin ⎝⎛⎭⎫π2－B ＝cos B ，故B 正确；对于C ，在△ABC 中，由a cos A ＝b cos B ，利用正弦定理可得sin 2A ＝sin 2B ，得到2A ＝2B 或2A ＝π－2B ，故A ＝B 或A ＝π2－B ，即△ABC是等腰三角形或直角三角形，故C 错误；对于D ，在△ABC 中，若B ＝60°，b 2＝ac ，由余弦定理可得，b 2＝a 2＋c 2－2ac cos B ，所以ac ＝a 2＋c 2－ac ，即(a －c )2＝0，解得a ＝c .又B ＝60°，所以△ABC 必是等边三角形，故D 正确．故选ABD.二、填空题7．(·济南联考改编)若tan(α＋2β)＝2，tan β＝－3，则tan(α＋β)＝________，tan α＝________．解析：因为tan(α＋2β)＝2，tan β＝－3，所以tan(α＋β)＝tan(α＋2β－β)＝tan （α＋2β）－tan β1＋tan （α＋2β）tan β＝2－（－3）1＋2×（－3）＝－1.tan α＝tan(α＋β－β)＝－1－（－3）1＋（－1）×（－3）＝12.答案：－1 128．已知a ，b ，c 是△ABC 中角A ，B ，C 的对边，a ＝4，b ∈(4，6)，sin 2A ＝sin C ，则c 的取值范围为________．解析：由4sin A ＝c sin C ，得4sin A ＝csin 2A ，所以c ＝8cos A ，因为16＝b 2＋c 2－2bc cos A ，所以16－b 2＝64cos 2A －16b cos 2A ，又b ≠4，所以cos 2A ＝16－b 264－16b ＝（4－b ）（4＋b ）16（4－b ）＝4＋b16，所以c 2＝64cos 2A ＝64×4＋b16＝16＋4b .因为b ∈(4，6)，所以32<c 2<40，所以42<c <210. 答案：(42，210)9．(一题多解)(·合肥市第一次质检测)设△ABC 的内角A ，B ，C 的对边a ，b ，c 成等比数列，cos(A －C )－cos B ＝12，延长BC 至点D ，若BD ＝2，则△ACD 面积的最大值为________．解析：法一：由题意知b 2＝ac ，由正弦定理得sin 2B ＝sin A sin C ①，又由已知，得cos(A －C )＋cos(A ＋C )＝12，可得cos A cos C ＝14 ②，②－①，得14－sin 2B ＝－cos B ，所以cos 2B ＋cos B －34＝0，解得cos B ＝12或cos B ＝－32(舍去)，所以B ＝60°，再由题得cos(A －C )＝1，则A－C ＝0，即A ＝C ，则a ＝c ，所以△ABC 为正三角形，则∠ACD ＝120°，AC ＝b ，CD ＝2－b ，故S △ACD ＝12×b ×(2－b )×32≤34⎝ ⎛⎭⎪⎫b ＋2－b 22＝34，当且仅当b ＝2－b ，即b ＝1时取等号．故填34. 法二：由题意知b 2＝ac ，且cos(A －C )＋cos(A ＋C )＝12，即cos A cos C ＋sin A sin C ＋cos A cosC －sin A sin C ＝12，即cos A cos C ＝14，由余弦定理得b 2＋c 2－a 22bc ·b 2＋a 2－c 22ab ＝14，整理得b 4－(a 2－c 2)2＝b 4，所以a 2－c 2＝0，即a ＝c ，又b 2＝ac ，所以a ＝b ＝c ，即△ABC 为正三角形，所以S △ACD ＝S △ABD －S △ABC ＝12×2×c ×32－34c 2＝－34(c －1)2＋34≤34，当c ＝1时取等号，故填34. 答案：34三、解答题10．(·广东六校第一次联考)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且a 2＋c 2－b 2＝ab cos A ＋a 2cos B .(1)求角B ；(2)若b ＝27，tan C ＝32，求△ABC 的面积． 解：(1)因为a 2＋c 2－b 2＝ab cos A ＋a 2cos B ，所以由余弦定理，得2ac cos B ＝ab cos A ＋a 2cos B ，又a ≠0，所以2c cos B ＝b cos A ＋a cos B ，由正弦定理，得 2sin C cos B ＝sin B cos A ＋sin A cos B ＝sin(A ＋B )＝sin C ，又C ∈(0，π)，sin C >0，所以cos B ＝12.因为B ∈(0，π)，所以B ＝π3.(2)由tan C ＝32，C ∈(0，π)，得sin C ＝217，cos C ＝277， 所以sin A ＝sin(B ＋C )＝sin B cos C ＋cos B sin C ＝32×277＋12×217＝32114. 由正弦定理a sin A ＝b sin B ，得a ＝b sin Asin B＝27×3211432＝6， 所以△ABC 的面积为12ab sin C ＝12×6×27×217＝6 3.11．(·武汉模拟)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，A ＝2B ，cos B ＝255.(1)求sin C 的值；(2)若角A 的平分线AD 的长为5，求b 的值． 解：(1)由cos B ＝255及0<B <π，得sin B ＝55，又A ＝2B ，所以sin A ＝sin 2B ＝2sin B cos B ＝2×55×255＝45， cos A ＝cos 2B ＝2cos 2B －1＝35.故sin C ＝sin(A ＋B )＝sin A cos B ＋cos A sin B ＝45×255＋35×55＝11525.(2)由题意得，∠ADC ＝B ＋12∠BAC ＝∠BAC (如图)，所以sin ∠ADC ＝45.在△ADC 中，AD sin C ＝ACsin ∠ADC ，即511525＝AC 45，AC ＝2011，故b ＝2011.12．(·高考天津卷)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知b ＋c ＝2a ，3c sin B ＝4a sin C .(1)求cos B 的值； (2)求sin ⎝⎛⎭⎫2B ＋π6的值． 解：(1)在△ABC 中，由正弦定理b sin B ＝csin C ，得b sin C ＝c sin B ，又由3c sin B ＝4a sin C ，得3b sin C ＝4a sin C ，即3b ＝4a .又因为b ＋c ＝2a ，得到b ＝43a ，c ＝23a .由余弦定理可得cos B＝a 2＋c 2－b 22ac ＝a 2＋49a 2－169a 22·a ·23a ＝－14.(2)由(1)可得sin B ＝1－cos 2B ＝154， 从而sin 2B ＝2sin B cos B ＝－158，cos 2B ＝cos 2B －sin 2B ＝－78， 故sin ⎝⎛⎭⎫2B ＋π6＝sin 2B cos π6＋cos 2B sin π6＝－158×32－78×12＝－35＋716. [B 组 大题增分专练]1．(·江西七校第一次联考)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知a (sin A －sin B )＝(c －b )(sin C ＋sin B )．(1)求角C ；(2)若c ＝7，△ABC 的面积为332，求△ABC 的周长．解：(1)由a (sin A －sin B )＝(c －b )(sin C ＋sin B )及正弦定理，得a (a －b )＝(c －b )(c ＋b )， 即a 2＋b 2－c 2＝ab .所以cos C ＝a 2＋b 2－c 22ab ＝12，又C ∈(0，π)，所以C ＝π3.(2)由(1)知a 2＋b 2－c 2＝ab ，所以(a ＋b )2－3ab ＝c 2＝7， 又S ＝12ab sin C ＝34ab ＝332，所以ab ＝6，所以(a ＋b )2＝7＋3ab ＝25，a ＋b ＝5. 所以△ABC 的周长为a ＋b ＋c ＝5＋7.2．(一题多解)(·福州模拟)如图，在△ABC 中，M 是边BC 的中点，cos ∠BAM ＝5714，cos ∠AMC ＝－277.(1)求∠B 的大小；(2)若AM ＝21，求△AMC 的面积．解：(1)由cos ∠BAM ＝5714，得sin ∠BAM ＝2114， 由cos ∠AMC ＝－277，得sin ∠AMC ＝217.又∠AMC ＝∠BAM ＋∠B ， 所以cos ∠B ＝cos(∠AMC －∠BAM ) ＝cos ∠AMC cos ∠BAM ＋sin ∠AMC sin ∠BAM ＝－277×5714＋217×2114＝－12，又∠B ∈(0，π)，所以∠B ＝2π3. (2)法一：由(1)知∠B ＝2π3，在△ABM 中，由正弦定理AM sin ∠B ＝BMsin ∠BAM ，得BM ＝AM sin ∠BAMsin ∠B＝21×211432＝ 3.因为M 是边BC 的中点， 所以MC ＝ 3.故S △AMC ＝12AM ·MC ·sin ∠AMC ＝12×21×3×217＝332.法二：由(1)知∠B ＝2π3，在△ABM 中，由正弦定理AM sin ∠B ＝BMsin ∠BAM ，得BM ＝AM sin ∠BAMsin ∠B＝21×211432＝ 3.因为M 是边BC 的中点，所以S △AMC ＝S △ABM ，所以S △AMC ＝S △ABM ＝12AM ·BM ·sin ∠BMA ＝12×21×3×217＝332.3．(·昆明市质量检测)△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，已知2(c －a cos B )＝3b .(1)求角A ；(2)若a ＝2，求△ABC 面积的取值范围．解：(1)由2(c －a cos B )＝3b 及正弦定理得2(sin C －sin A cos B )＝3sin B ， 所以2sin(A ＋B )－2sin A cos B ＝3sin B ，即2cos A sin B ＝3sin B ， 因为sin B ≠0，所以cos A ＝32，又0<A <π，所以A ＝π6. (2)因为a ＝2，由正弦定理得b ＝4sin B ，c ＝4sin C ， 所以S △ABC ＝12bc sin A ＝14bc ，所以S △ABC ＝4sin B sin C ，因为C ＝π－(A ＋B )＝5π6－B ，所以sin C ＝sin ⎝⎛⎭⎫5π6－B ， 所以S △ABC ＝4sin B sin ⎝⎛⎭⎫5π6－B ＝4sin B ⎝⎛⎭⎫12cos B ＋32sin B ，即S △ABC ＝2sin B cos B ＋23sin 2B ＝sin 2B －3cos 2B ＋ 3 ＝2sin ⎝⎛⎭⎫2B －π3＋ 3. 因为0<B <5π6，所以－π3<2B －π3<4π3，所以－32<sin ⎝⎛⎭⎫2B －π3≤1， 所以0<S △ABC ≤2＋ 3.即△ABC 面积的取值范围为(0，2＋3]．4．已知在△ABC 中，角A ，B ，C 所对的边长分别为a ，b ，c ，AB 边上的高h ＝23c .(1)若△ABC 为锐角三角形，且cos A ＝35，求角C 的正弦值；(2)若C ＝π4，M ＝a 2＋b 2＋13c 2ab，求M 的值．解：(1)作CD ⊥AB ，垂足为D ，因为△ABC 为锐角三角形，且cos A ＝35，所以sin A ＝45，tan A ＝43，所以AD ＝c 2，BD ＝AB －AD ＝c2，所以BC ＝CD 2＋BD 2＝⎝⎛⎭⎫23c 2＋⎝⎛⎭⎫c 22＝5c 6，由正弦定理得sin ∠ACB ＝AB sin ABC ＝c ×455c 6＝2425.(2)因为S △ABC ＝12c ×23c ＝12ab sin ∠ACB ＝24ab ，所以c 2＝324ab ，又a 2＋b 2－c 2＝2ab cos ∠ACB ＝2ab ， 所以a 2＋b 2＝2ab ＋c 2，所以a 2＋b 2＋13c 2＝2ab ＋43c 2＝2ab ＋43×324ab ＝22ab ，所以M ＝a 2＋b 2＋13c 2ab ＝22abab ＝2 2.。

考点20 三角恒等变换1．设α，β∈[0，π]，且满足sin αcos β－cos αsin β＝1，则sin(2α－β)＋sin(α－2β)的取值范围为( ) A ．[－2，1] B ．[－1，2] C ．[－1,1] D ．[1，2]【答案】C2．已知2sin 2θ＋sin 2θ1＋tan θ＝k,0<θ<π4，则sin ⎝⎛⎭⎫θ－π4的值为( ) A ．随着k 的增大而增大B ．有时随着k 的增大而增大，有时随着k 的增大而减小C ．随着k 的增大而减小D ．是与k 无关的常数 【答案】A【解析】2sin 2θ＋sin 2θ1＋tan θ＝2sin θθ＋cos θsin θ＋cos θcos θ＝2sin θcos θ＝sin 2θ，∵0<θ<π4，∴0<sin θ<22<cosθ<1,0<2θ<π2，∴k ＝sin 2θ∈(0,1)，(sin θ－cos θ)2＝1－sin 2θ，sin θ－cos θ＝－1－sin 2θ＝－1－k ，故sin ⎝⎛⎭⎫θ－π4＝22(sin θ－cos θ)＝－2－2k 2，其值随着k 的增大而增大，故选A. 3．函数在区间上的最大值为______．【答案】【解析】函数；∵，∴当时，取得最大值为，故答案为.4．在锐角三角形ABC 中，已知2sin2 A+ sin2B = 2sin2C，则的最小值为___．【答案】故答案为：.5．已知，则______．【答案】【解析】∵，∴.故答案为：6．三角形ABC中，，AC=1，以B为直角顶点作等腰直角三角形BCD（A、D在BC两侧），当∠BAC变化时，线段AD的长度最大值为._______________.【答案】3＝5﹣2cos∠BAC+2sin∠BAC＝5+4sin（∠BAC﹣45°），∴当∠BAC＝135°时AD2最大为9，AD最大值为3，故答案为：3．7．在平面直角坐标系中，角的顶点在原点，始边与轴的非负半轴重合，终边过点，则__________.【答案】【解析】，所以.8．计算：______【答案】9．对于三次函数有如下定义：设是函数的导函数，是函数的导函数，若方程有实数解，则称点为函数的“拐点”。

高三数学三角函数三角恒等变换解三角形试题答案及解析1.已知中，那么角=【答案】π/4【解析】略2.已知f(α)＝(1)化简f(α)；(2)若α是第三象限角，且cos(α－)＝，求f(α)的值．【答案】(1)f(α)＝＝－cosα.(2)∵α是第三象限角，且cos(α－)＝－sinα＝，∴sinα＝－，∴cosα＝－＝－，∴f(α)＝－cosα＝.【解析】略3.已知函数为奇函数，且，其中（1）求的值;（2）若，求的值．【答案】（1） , ；（2）【解析】（1）由为奇函数，可得，函数化为，又根据可求；（2）由（1）可得，由得又因为，所以，再根据两角和的正弦可求试题解析：因为为奇函数，所以，，则（2），因为，即又因为，所以，【考点】函数的奇偶性，三角函数的性质4.设命题函数是奇函数；命题函数的图象关于直线对称．则下列判断正确的是（）A．为真B．为假C．为假D．为真【答案】C【解析】因为是偶函数，所以命题是假命题，由余弦函数的性质可知命题是假命题，选项C正确.【考点】1.三角函数性质；2.逻辑联结词与命题.5.（本小题满分12分）某同学用五点法画函数在某一个周期内的图像时，列表并填入了部分数据，如下表：5-5（1）请将上表数据补充完整，并直接写出函数的解析式；（2）若函数的图像向左平移个单位后对应的函数为，求的图像离原点最近的对称中心．【答案】（1）；（2）．【解析】第一问结合三角函数的性质，确定出对应的值，完善表格，从而确定出函数解析式，第二问利用图形的平移变换，将函数的解析式求出来，利用函数的性质，找出函数图像的对称中心，给赋值，比较从而确定出离原点最近的对称中心．试题解析：（1）根据表中已知数据，解得数据补全如下表：050-50函数表达式为（2）函数图像向左平移个单位后对应的函数是，其对称中心的横坐标满足，所以离原点最近的对称中心是．【考点】三角函数的性质，图像的变换．6.（本小题满分10分）已知函数．（1）求的最小正周期；（2）设，求的值域和单调递减区间．【答案】（1）；（2）【解析】（1）先根据二倍角公式和两角和与差的公式进行化简，再求出周期即可；（2）先根据x的范围求得，再结合正弦函数的性质可得到函数f（x）的值域，求得单调递减区间．试题解析：（1）（2）∵，，的值域为．的递减区间为．【考点】三角函数的周期性及其求法；正弦函数的定义域和值域；正弦函数的单调性7.（本小题满分12分）在中，角的对边分别为，已知，向量，且∥．（1）求角的大小；（2）若成等差数列，求边的大小．【答案】（1）；（2）【解析】（1）利用数量积运算、正弦定理即可得出；（2）由成等差数列，可得，或，即2a=b．再利用直角三角形的边角关系、余弦定理即可得出．试题解析：（1）∥，得，由正弦定理可得，（2）成等差，所以化简整理得：即或得或若若【考点】正弦定理；平面向量数量积运算8.在中，角所对的边为．已知，且．（1）求的值；（2）当时，求的面积．【答案】（1）；（2）．【解析】（1）根据已知条件中的式子，结合正弦定理，将其化为的方程，即可求解；（2）利用已知条件，结合余弦定理，可求得，的值，再利用三角形面积计算公式即可求得的值．试题解析：（1）∵，∴①，又∵，∴②，联立①②，即可求得，；（2）由（1）结合余弦定理可知，或，由已知易得，∴，∴，．【考点】1．正余弦定理解三角形；2．三角恒等变形．9.（本题满分12分）已知，,函数．（1）求的最小正周期，并求其图像对称中心的坐标；（2）当时，求函数的值域．【答案】（1）的最小正周期为，其对称中心的坐标为（）（）；（2）的值域为．【解析】（1）先用降幂公式和辅助角公式，将进行化简整理得到，然后根据正弦函数的周期公式可得函数的最小正周期，进而求出函数的零点，即为函数的图像对称中心的坐标；（2）根据可得到，最后结合正弦函数的图像与性质可得函数的值域．试题解析：（1）因为=，所以的最小正周期为，令，得，∴故所求对称中心的坐标为（）（）．（2）∵，∴，∴，即的值域为．【考点】1、三角函数中的恒等变换；2、三角函数的周期性及其求法；3、正弦函数的图像及其性质．【方法点晴】本题考查了三角函数中的恒等变换、三角函数的周期性及其求法和正弦函数的图像及其性质，重点考查学生对三角函数的基本概念、基本性质和基本原理，属中档题．解决这类问题最关键的一步是运用降幂公式、倍角公式及三角函数的和差公式等将函数的表达式化简为同角的正弦或余弦形式．因此需要大家应熟练掌握相关公式并结合三角函数的图像及其性质进行求解．10.若函数在上单调递减，且在上的最大值为，则的值为（）A．B．C．D．【答案】A【解析】由题意得：，解得，选A．【考点】正切函数性质11.（本小题满分12分）已知向量，．（1）当时，求的值；（2）设函数，已知在中，内角、、的对边分别为、、，若，，，求当时，的取值范围．【答案】（1）；（2）．【解析】（1）平方关系和商数关系式中的角都是同一个角，且商数关系式中，利用，得出，把转化为的式子，从而求解；（2）熟悉三角公式的整体结构，灵活变换，要熟悉三角公式的代数结构，更要掌握公式中角和函数名称的特征，要体会公式间的联系，掌握常见的公式变形，倍角公式应用是重点，涉及倍角或半角的都可以利用倍角公式及其变形，把形如化为，研究函数的性质由的取值范围确定的取值范围，再确定的取值范围．试题解析：（1），，，（2）由正弦定理得，得或，，因此，，即．【考点】1、同角三角函数的基本关系；2、三角函数的化简；3、求三角函数的值域．12.（2012秋•泰安期中）已知函数f（x）=2sinωxcosωx﹣2sin2ωx+（ω＞0），直线x=x1，x=x2是函数y=f（x）的图象的任意两条对称轴，且|x1﹣x2|的最小值为．（Ⅰ）求ω的值；（Ⅱ）求函数f（x）的单调增区间；（Ⅲ）若f（α）=，求sin（π﹣4α）的值．【答案】（Ⅰ）1；（Ⅱ）见解析；（Ⅲ）﹣．【解析】（I）利用二倍角公式即辅助角公式，化简函数，利用直线x=x1，x=x2是函数y=f（x）的图象的任意两条对称轴，且|x1﹣x2|的最小值为，可得函数的最小正周期为π，根据周期公式，可求ω的值；（II）利用正弦函数的单调性，可得函数f（x）的单调增区间；（III）由f（a）=，可得sin（2a+）=，根据sin（π﹣4a）=sin[﹣2（2a+）]=﹣cos[2（2a+）]=2sin2（2a+）﹣1，即可求得结论．解：（I）∵f（x）=2sinωxcosωx﹣2sin2ωx+=sin2ωx+cos2ωx=2sin（2ωx+）∵直线x=x1，x=x2是函数y=f（x）的图象的任意两条对称轴，且|x1﹣x2|的最小值为，∴函数的最小正周期为π∴=π∴ω=1；（II）由（I）知，f（x）=2sin（2x+）∴﹣+2kπ≤2x+≤+2kπ，k∈Z∴﹣+kπ≤x≤+kπ，k∈Z∴函数f（x）的单调增区间为[﹣+kπ，+kπ]，k∈Z；（III）∵f（a）=，∴sin（2a+）=∴sin（π﹣4a）=sin[﹣2（2a+）]=﹣cos[2（2a+）]=2sin2（2a+）﹣1=﹣．【考点】三角函数中的恒等变换应用；由y=Asin（ωx+φ）的部分图象确定其解析式；复合三角函数的单调性．13.已知向量，且函数在时取得最小值．（Ⅰ）求的值；（Ⅱ）在中，分别是内角的对边，若，，，求的值．【答案】（Ⅰ）；（Ⅱ）【解析】（Ⅰ）利用向量的数量积公式，结合辅助角公式，求的值；（Ⅱ）先求出，再利用正弦定理，即可求的值．试题解析：（Ⅰ）由于（Ⅱ）由上知,于是由正弦定理得:【考点】正弦定理，余弦定理，两角和与差的三角函数，向量的数量积14.已知，函数在单调递减，则的取值范围是．【答案】【解析】，，由题意，所以，由于，所以只有，．【考点】三角函数的单调性．【名师】求形如y＝Asin（ωx＋φ）或y＝Acos（ωx＋φ）（其中A≠0，ω＞0）的函数的单调区间，可以通过解不等式的方法去解答，列不等式的原则是：①把“ωx＋φ（ω＞0）”视为一个“整体”；②A＞0（A＜0）时，所列不等式的方向与y＝sin x（x∈R），y＝cos x（x∈R）的单调区间对应的不等式方向相同（反）．15.（2015秋•南京校级期中）将函数f（x）=2sin（2x﹣）的图象向左平移m个单位（m＞0），若所得的图象关于直线x=对称，则m的最小值为．【答案】【解析】由条件利用函数y=Asin（ωx+φ）的图象变换规律，正弦函数的图象的对称性，求得m的最小值．解：将函数f（x）=2sin（2x﹣）的图象向左平移m个单位（m＞0），可得y=2sin[2（x+m）﹣]=2sin（2x+2m﹣）的图象．∵所得的图象关于直线x=对称，∴2•+2m﹣=kπ+，k∈Z，即 m=+，k∈Z，则m的最小值为，故答案为：．【考点】函数y=Asin（ωx+φ）的图象变换．16.（2015秋•昌平区期末）已知函数．（Ⅰ）求函数f（x）的最小正周期；（Ⅱ）求函数f（x）的单调递减区间．【答案】（Ⅰ）；（Ⅱ）函数f（x）的单调递减区间是．）【解析】（Ⅰ）利用三角函数的倍角公式以及辅助角公式进行化简，即可求函数f（x）的最小正周期；（Ⅱ）利用三角函数的单调性即可求函数f（x）的单调递减区间．解：（Ⅰ）==所以最小正周期．（Ⅱ）由，得．所以函数f（x）的单调递减区间是．）【考点】三角函数中的恒等变换应用；正弦函数的图象．17.已知函数．（1）求的最小正周期和在上的单调递减区间；（2）若为第四象限角，且，求的值．【答案】（1）；（2）．【解析】（1）对的表达式进行三角恒等变形，利用三角函数的性质即可求解；（2）利用同角三角函数的基本关系求得的值后即可求解．试题解析：（1）由已知，所以最小正周期，由，得，故函数在上的单调递减区间；（2）因为为第四象限角，且，所以，所以．【考点】三角函数综合．18.已知是第二象限角，且，则（）A．B．C．D．【答案】C【解析】由,得，又∵是第二象限角,∴，∴原式=；故选C．【考点】1.诱导公式；2.同角三角函数基本关系式．19.在中，角所对的边分别为，且，则的最大值为_____.【答案】【解析】由及正弦定理得，又因为，于是可得，所以，所以，则的最大值为，故答案填.【考点】1、正弦定理；2、两角和与差的三角函数；3、基本不等式.20.将函数图象上各点的横坐标伸长到原来的倍，再向左平移个单位，纵坐标不变，所得函数图象的一条对称轴的方程是（）A．B．C．D．【答案】D【解析】将函数图象上各点的横坐标伸长到原来的倍，得，再向左平移个单位，得，令，解得，令，得，即所得函数图象的一条对称轴的方程是，故选D．【考点】三角函数的图象变换与三角函数的性质．21.设平面向量.（1）若，求的值；（2）若，求的取值范围.【答案】（1）；（2）.【解析】（1）先利用向量数量积的坐标表示求出，利用商数关系求出得值，再利用二倍角公式求出的值，最后代入到的展开式即可求得；（2）欲求，先求出，再根据求的范围，从而可得的取值范围.试题解析：（1）因为，所以，∴，∴.（2），，.【考点】1、向量数量积的坐标表示；2、二倍角公式；3、三角函数；4、商数关系；5、向量的模．22.设中的内角所对的边长分别为，且.（1）当时，求角的度数；（2）求面积的最大值.【答案】（1）；（2）.【解析】（1）求出,再由正弦定理求出,求出角；（2）求三角形面积的最大值,即求的最大值,由,,求出,就可以求出面积的最大值.试题解析：解：（1）因为，所以.因为，由正弦定理可得.因为，所以是锐角，所以.（2）因为的面积，所以当最大时，的面积最大.因为，所以.因为，所以，所以（当时等号成立）.所以面积的最大值为.【考点】1.正弦定理；2.余弦定理；3.重要不等式.23.在中，内角的对边为，已知.（1）求角的值；（2）若，且的面积为，求.【答案】（1）；（2）.【解析】根据正弦定理可得，根据内角和定理和两角和的正弦公式整理可得，即得角的值；（2）由的面积为，求得的值，根据余弦定理表示构造的另一个方程，解方程组即可求得.试题解析：（1）∵，∴，∴，即，∴，∴，又∵是三角形的内角，∴（2）∵，∴，∴，又∵，∴，∴，∴【考点】正余弦定理解三角形.24.的三个内角满足：，则（）A．B．C．D．或【答案】B【解析】由已知条件以及正弦定理可得：，即，再由余弦定理可得，所以，故选B.【考点】正弦定理、余弦定理.25.在中，角，，的对边分别是，，，已知，．（I）求的值；（II）若角为锐角，求的值及的面积．【答案】（I）；（II）【解析】（I）根据题意和正弦定理求出a的值；（II）由二倍角的余弦公式变形求出sin2A，由A 的范围和平方关系求出cosA，由余弦定理列出方程求出b的值，代入三角形的面积公式求出△ABC的面积．试题解析：（I）因为，且，所以．因为，由正弦定理，得．（II）由得．由余弦定理，得．解得或（舍负）．所以．【考点】正弦定理；余弦定理26.如图所示的是函数和函数的部分图象，则函数的解析式是（）A．B．C．D．【答案】C.【解析】由题意得，，故排除B，D；又∵，故排除A，故选C.【考点】三角函数的图象和性质．27.已知，则=（）A．B．C．D．【答案】A【解析】，故选A．【考点】和差倍半的三角函数．28.在中，角所对的边分别为,．（Ⅰ）求的值；（Ⅱ）若，，求的面积．【答案】（Ⅰ）（Ⅱ）【解析】（Ⅰ）先根据正弦定理将边统一成角：，再利用三角形内角关系、诱导公式、两角和正弦公式将三角统一成两角：，最后根据同角三角函数关系将弦化切：（Ⅱ）由（Ⅰ）易得，已知两角一对边，根据正弦定理求另一边：，利用三角形内角关系求第三角的正弦值：，最后根据面积公式求面积：试题解析：解：（Ⅰ）由及正弦定理得.所以,所以.（Ⅱ）,所以, ,,所以的面积为.【考点】正弦定理，弦化切【方法点睛】解三角形问题，多为边和角的求值问题，这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系，从而达到解决问题的目的.其基本步骤是：第一步：定条件即确定三角形中的已知和所求，在图形中标出来，然后确定转化的方向.第二步：定工具即根据条件和所求合理选择转化的工具，实施边角之间的互化.第三步：求结果.29.同时具有性质“①最小正周期是，②图象关于直线对称；③在上是增函数”的一个函数是（）A．B．C．D．【答案】C【解析】由题意得，函数的最小周期为，则，又函数图象关于直线对称，则函数为函数的最小值，则只有B、C满足，由当时，，则函数是单调递增函数，故选C．【考点】三角函数的性质．30.若函数的最大值为5，则常数______.【答案】【解析】，其中，故函数的最大值为，由已知得，，解得.【考点】三角函数的图象和性质.【名师】解决三角函数性质问题的基本思路是通过化简得到，结合角的范围求解.. 本题难度不大，能较好地考查考生的逻辑推理能力、基本计算能力等.31.定义在区间[0，]上的函数的图象与的图象的交点个数是 .【答案】7【解析】由，因为，所以故两函数图象的交点个数是7.【考点】三角函数图象【名师】求函数图象的交点个数，有两种方法：一是直接求解，如本题，解一个简单的三角方程，此方法立足于易于求解；二是数形结合，分别画出函数图象，数出交点个数，此法直观，但对画图要求较高，必须准确，尤其是要明确函数的增长幅度.32.△ABC的内角A、B、C的对边分别为a、b、c.已知，，，则b=（A）（B）（C）2 （D）3【答案】D【解析】由余弦定理得，解得（舍去），选D.【考点】余弦定理【名师】本题属于基础题,考查内容单一,根据余弦定理整理出关于b的一元二次方程,再通过解方程求b.运算失误是基础题失分的主要原因,请考生切记！33.将函数y=2sin（2x+）的图像向右平移个周期后，所得图像对应的函数为A．y=2sin（2x+）B．y=2sin（2x+）C．y=2sin（2x–）D．y=2sin（2x–）【答案】D【解析】函数的周期为，将函数的图像向右平移个周期即个单位，所得图像对应的函数为，故选D.【考点】三角函数图像的平移【名师】函数图像的平移问题易错点有两个,一是平移方向,注意“左加右减”；二是平移多少个单位是对x而言的,不要忘记乘以系数.34.如图，在Rt△ABC中，AC⊥BC，D在边AC上，已知BC＝2，CD＝1，∠ABD＝45°，则AD＝．【答案】5【解析】，，所以，．【考点】解三角形．【名师】在解直角三角形时，直角三角形中的三角函数定义是解题的桥梁，利用它可以很方便地建立边与角之间的关系．35.设函数的部分图象如图所示，直线是它的一条对称轴，则函数的解析式为（）A．B．C．D．【答案】C【解析】因为直线是它的一条对称轴，排除B，D，因为图象过点，排除选项A,选C.【考点】三角函数图象与性质.36.在中，角，，的对边分别为，，，且满足，则角等于（）A．B．C．D．【答案】A【解析】由正弦定理可得，即，由余弦定理可得，所以，故应选A。

2019湖南高考数学二轮练习-三角恒等变换注意事项：认真阅读理解，结合历年的真题，总结经验，查找不足！重在审题，多思考，多理解！无论是单选、多选还是论述题，最重要的就是看清题意。

在论述题中，问题大多具有委婉性，尤其是历年真题部分，在给考生较大发挥空间的同时也大大增加了考试难度。

考生要认真阅读题目中提供的有限材料，明确考察要点，最大限度的挖掘材料中的有效信息，建议考生答题时用笔将重点勾画出来，方便反复细读。

只有经过仔细推敲，揣摩命题老师的意图，积极联想知识点，分析答题角度，才能够将考点锁定，明确题意。

I 卷【一】选择题1、计算1－2sin 222.5°的结果等于()A 、12B 、22C 、33D 、32 【答案】B2、函数y ＝2cos 2⎝⎛⎭⎫x －π4－1是()A 、最小正周期为π的奇函数B 、最小正周期为π的偶函数C 、最小正周期为π2的奇函数D 、最小正周期为π2的偶函数【答案】A3、函数y ＝sin ⎝⎛⎭⎫x －π6cos x 的最大值为()A 、12B 、14C 、1D 、22【答案】B4、以下各式与tan α相等的是()A 、1－cos2α1＋cos2αB 、sin α1＋cos αC 、sin α1－cos2αD 、1－cos2αsin2α【答案】D5、△ABC 的三内角A 、B 、C 的对边边长分别为a 、b 、c .假设a ＝52b ，A ＝2B ，那么cos B ＝()A 、53B 、54C 、55D 、56 【答案】B6、cos α＝45，且32π<α<2π，那么tan α2等于()A 、－13B 、13C 、－13或13D 、－3 【答案】A7、函数f (x )＝sin 2x ＋3sin x cos x 在区间π4，π2上的最大值是()A 、1B 、1＋32C 、32D 、1＋ 3【答案】C8、角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x 上，那么cos2θ＝()A 、－45B 、－35C 、35D 、45【答案】B9、假设tan α＝3，那么sin2αcos 2α的值等于()A 、2B 、3C 、4D 、6【答案】D10、函数f (x )＝3sin ωx ＋cos ωx (ω＞0)，y ＝f (x )的图象与直线y ＝2的两个相邻交点的距离等于π，那么f (x )的单调递增区间是()A 、⎣⎡⎦⎤k π－π12，k π＋5π12，k ∈ZB 、⎣⎡⎦⎤k π＋5π12，k π＋11π12，k ∈ZC 、⎣⎡⎦⎤k π－π3，k π＋π6，k ∈ZD 、⎣⎡⎦⎤k π＋π6，k π＋2π3，k ∈Z【答案】C11、cos39°cos(－9°)－sin39°sin(－9°)等于()A 、12B 、32C 、－12D 、－32 【答案】B12、假设0tan sin <αα，那么α2cos 1+等于〔〕 A 、αcos 2 B 、-αcos 2 C 、αsin 2 D 、-αsin 2【答案】BII 卷【二】填空题13、函数y ＝cos ⎝⎛⎭⎫x ＋π3cos ⎝⎛⎭⎫x ＋2π3的最大值是______、【答案】3414、sin ⎝⎛⎭⎫α－π4＝35，α∈⎝⎛⎭⎫0，π2，那么sin α＝________.【答案】721015、cos(π－2α)sin(α－π4)＝－22，那么sin α＋cos α＝________.【答案】－1216、0<α<π4，β为f (x )＝cos ⎝⎛⎭⎫2x ＋π8的最小正周期，a ＝⎝⎛⎭⎫tan ⎝⎛⎭⎫α＋14β，－1，b ＝(cos α，2)，且a ·b ＝m ，那么2cos 2α＋sin 2(α＋β)cos α－sin α＝________. 【答案】4＋2m【三】解答题17、【答案】222222222222222223sin 5cos cos 3sin 5cos cos cos cos cos cos cos 4tan 3tan 5423251tan 121os os αααααααααααααααααααα--+--=+--⨯-⨯-===++4sin （2）sin 4sin sin18、在△ABC 中，假设B ＝30°，求cos A sin C 的取值范围、【答案】由题意得cos A sin C ＝12sin(A ＋C )－sin(A －C )＝12sin(π－B )－sin(A －C )＝14－12sin(A －C )、∵－1≤sin(A －C )≤1，∴－14≤14－12sin(A －C )≤34，∴cos A sin C 的取值范围是⎣⎡⎦⎤－14，34、19、函数f (x )＝2sin(π－x )cos x .(1)求f (x )的最小正周期；(2)求f (x )在区间⎣⎡⎦⎤－π6，π2上的最大值和最小值、【答案】(1)∵f (x )＝2sin(π－x )cos x＝2sin x cos x ＝sin2x ，∴函数f (x )的最小正周期为π.(2)由－π6≤x ≤π2⇒－π3＜2x ≤π， ∴－32≤sin2x ≤1，∴f (x )在区间⎣⎡⎦⎤－π6，π2上的最大值为1，最小值为－32、20、函数1()2sin(),.36f x x x R π=-∈ (Ⅰ〕求5()4f π的值；(Ⅱ〕设，，，，、56)23(1310)23(20=+=+⎥⎦⎤⎢⎣⎡∈πβπαπβαf f 求cos()αβ+的值. 【答案】(Ⅰ)55()2sin()2sin 41264f ππππ=-==. (Ⅱ〕1310sin 2]6)23(31sin[2)23(==-+=+αππαπαf ，5sin 13α∴=， 又[0,]2πα∈，12cos 13α∴=. 56cos 2)2sin(2]6)23(31sin[2)23(==+=-+=+βπβππβπβf ，3cos 5β∴=， 又[0,]2πβ∈，4sin 5β∴=， 所以16cos()cos cos sin sin 65αβαβαβ+=-=.21、如图，在平面直角坐标系xOy 中，以Ox 轴为始边做两个锐角α、β，它们的终边分别与单位圆相交于A 、B 两点，A 、B的横坐标分别为,105、(Ⅰ〕求)tan(βα+的值；(Ⅱ〕求2αβ+的值、【答案】由条件及三角函数的定义可知，cos αβ==因为α,β为锐角，所以.55cos 1sin ,1027cos 1in 22=-==-=ββααs 因此.21cos sin tan ,7cos sin tan ====βββααα(Ⅰ〕.32171217tan tan 1tan tan )(tan -=⨯-+=-+=+βαβαβα(Ⅱ〕解法一：ββαββαβαtan )tan(1tan )tan()2(tan +-++=+.121)3(1213-=⨯--+-=.432πβα=+∴ 解法二：因为22tan 4tan 21tan 3βββ==-，所以()tan tan 2tan 211tan tan 2αβαβαβ++==--..432πβα=+∴22、复数z 1＝sin2x ＋λi ，z 2＝m ＋(m －3cos2x )i(λ，m ，x ∈R)，且z 1＝z 2.(1)假设λ＝0且0<x <π，求x 的值；(2)设λ＝f (x )，当x ＝α时，λ＝12，试求cos ⎝⎛⎭⎫4α－2π3 的值、【答案】(1)∵z 1＝z 2，∴⎩⎪⎨⎪⎧ sin2x ＝m ，λ＝m －3cos2x .∴λ＝sin2x －3cos2x ，假设λ＝0，那么sin2x －3cos2x ＝0，得tan2x ＝3、 ∵0<x <π，∴0<2x <2π.∴2x ＝π3或2x ＝4π3、∴x ＝π6或2π3、(2)∵λ＝f (x )＝sin2x －3cos2x＝2⎝ ⎛⎭⎪⎫12sin2x －32cos2x＝2⎝⎛⎭⎫sin2x cos π3－cos2x sin π3＝2sin ⎝⎛⎭⎫2x －π3，又∵当x ＝α时，λ＝12，∴2sin ⎝⎛⎭⎫2α－π3＝12，sin ⎝⎛⎭⎫2α－π3＝14， ∴cos(4α－2π3)＝1－2sin 2(2α－π3) ＝1－2×116＝78、。