色谱速率理论武汉大学

第四章速率理论一范·第姆特（Van Deemter）方程二戈莱（Golay）方程三范·第姆特（Van Deemter）曲线四色谱柱和色谱操作参数的调整和统一⒈涡流扩散项（A项）中参数的调整和统一⒉气相分子扩散项（B项）中参数的调整和统一⒊气相传质阻力项（C项）中参数的调整和统一g项）中参数的调整和统一⒋液相传质阻力项（Cl五在气相色谱法中样品的分离第四章速率理论4-1第四章速率理论在第三章中我们已经宏观地讨论了柱的溶剂效率和塔板理论。

在溶剂效率方面，我们讨论了样品组分（以下简称“组分”）在指定固定液上的分配系数K，它决定了组分在色谱柱上的相对保留值α，且组分的分配系数K和相对保留值α均为温度的函数；在塔板理论中，我们利用克莱格二项式分布的多级萃取过程来解释组分在色谱过程中的色带展宽，并由此引出了柱效率的概念，以及可以用理论塔板数或有效理论塔板数来评价柱效率的高低。

根据有效理论塔板数N的计算式可知，这说明色带的展宽与色谱柱的有效理论塔板数的平方根是成正比的。

在线性分布等温线理想色谱法中，我们基于如下假设：①色谱柱内的所有各点的分配都相等；②载气的流速是均匀的；③在两相内都不存在样品组分分子（以下简称“组分分子”）的轴向分子扩散；④两相间的平衡在瞬间完成，不存在质量传递阻力。

从宏观上考虑，除由于柱顶端到柱尾部间存在的压差使载气流速不可能在柱中保持一致外，其它的假设似乎都能成立；但是，从微观的方面考虑，以下这些现象都是影响柱分离效率的因素：首先，由于柱管本身的长度、内径以及固定相对载气流动的阻力，整个色谱柱内都存在着压力梯度，即沿柱的方向从柱顶端到柱尾部的载气压力将逐点下降，同时沿此方向的载气流速和载气分子的线速度却在逐点升高（见图4-1示意）。

图4-1色谱柱内的压力梯度对载气流速的影响此外，在柱管管壁，特别是在毛细管柱的涂有固定液液膜的管壁上，载气分子的线速度将由于摩擦阻力而减速，而沿柱管中心流动的载气分子因较少这种阻力而移动得相对地较快，这种“莱4-2现代气相色谱实践曼流动”（Laminar flow）使柱管壁对柱管中心产生压差（图4-2）。

简述色谱基础理论中的塔板理论和速率理论塔板理论是由以下四个假设构成的：1、在柱内一小段长度H内，组分可以在两相间迅速达到平衡。

这一小段柱长称为理论塔板高度H。

2、流动相（如载气）进入色谱柱不是连续进行的，而是脉动式，每次进气为一个塔板体积（ΔVm）。

3、所有组分开始时存在于第0号塔板上，而且试样沿轴（纵）向扩散可忽略。

4、分配系数在所有塔板上是常数，与组分在某一塔板上的量无关。

（3分）速率理论：是由荷兰学者范弟姆特等提出的。

结合塔板理论的概念，把影响塔板高度的动力学因素结合进去，导出的塔板高度H与载气线速度u的关系：H?A?B?Cuu其中：A 称为涡流扩散项，B 为分子扩散项，C 为传质阻力项涡流扩散项A 气体碰到填充物颗粒时，不断地改变流动方向，使试样组分在气相中形成类似“涡流”的流动，因而引起色谱的扩张。

由于A=2λdp ，表明A 与填充物的平均颗粒直径dp 的大小和填充的不均匀性λ有关，而与载气性质、线速度和组分无关，因此使用适当细粒度和颗粒均匀的担体，并尽量填充均匀，是减少涡流扩散，提高柱效的有效途径。

分子扩散项B/u 由于试样组分被载气带入色谱柱后，是以“塞子”的形式存在于柱的很小一段空间中，在“塞子”的前后( 纵向) 存在着浓差而形成浓度梯度，因此使运动着的分子产生纵向扩散。

而B=2rDg r 是因载体填充在柱内而引起气体扩散路径弯曲的因数( 弯曲因子) ， D g为组分在气相中的扩散系数。

分子扩散项与 D g 的大小成正比，而 D g 与组分及载气的性质有关：相对分子质量大的组分，其 D g 小, 反比于载气密度的平方根或载气相对分子质量的平方根，所以采用相对分子质量较大的载气( 如氮气) ，可使 B 项降低， D g 随柱温增高而增加，但反比于柱压。

弯曲因子r 为与填充物有关的因素。

传质项系数Cu C 包括气相传质阻力系数 C g 和液相传质阻力系数 C 1 两项。

所谓气相传质过程是指试样组分从移动到相表面的过程，在这一过程中试样组分将在两相间进行质量交换，即进行浓度分配。

简述色谱速率理论及各项意义
色谱速率理论是一种研究物质在不同温度和压力条件下分离的
理论。

它可以帮助科学家们了解物质在色谱分离中的过程，有助于提高和优化色谱分离的效率和质量。

色谱速率理论的基本原理是：物质在某一温度或压力下，在某一色谱介质中的分离速度是确定的。

物质的分离影响因素包括色谱介质的粘度、对流、溶解度和温度等，以及每一分离步骤的时间和条件参数等等。

色谱速率理论有许多实际应用，其中最普遍的是分离物质的质量和纯度。

它可以用来控制色谱仪器，以便达到理想的物质分离效果。

另外，色谱速率理论还可以用来调节流动相中的比热容，降低色谱分离温度，增加分离效率，提高分离质量，以及提高分离质量。

此外，色谱速率理论还可以用于研究物质的峰积分离、衍生物分离和电喷雾分离等技术的控制及效率提升。

该理论的发展促进了物质的色谱分离研究，为制备更高纯度的药物和更高精度的化学分析提供了新的思路。

综上所述，色谱速率理论是一门关于物质从一种色谱介质中分离出来的过程。

它在物质分离得到质量和纯度更高的产品，物质分离技术控制和效率提升等方面发挥着重要作用。

它为科学家们探索物质的色谱分离新方法提供了基础，同时也能帮助科学家们更好地控制并优化色谱仪器的性能。

- 1 -。

气相色谱分析速率理论速率理论是从动力学观点动身，按照基本的试验事实讨论各种操作条件(载气的性质及流速、固定液的液膜厚度、载体颗粒的直径、色谱柱填充的匀称程度等)对理论塔板高度的影响，从而说明在色谱柱中色谱峰形扩张的缘由。

其可用范第姆特(Van Deemter)方程式表示。

范第姆特等人认为使色谱峰扩张的缘由是受涡流蔓延、分子蔓延、气液两相的传质阻力的影响，因而导出速率方程式或称范氏方程：式中λ—固定相填充不匀称因子； dp—载体的平均颗粒直径，Gm; γ—载体颗粒大小不同而引起的气体蔓延路径弯曲因子，简称弯曲因子； Dg—组分在气相中的蔓延系数，cm2/s; k—分配比； df—固定液在载体上的液膜厚度，cm; Dl—组分在液相中的蔓延系数，cm2/s; u—载气在柱中的平均线速度，cm/s。

范氏方程可简化为下式：式中，A为涡流蔓延项；为分子蔓延项；Cu为传质阻力项。

范氏方程的研究如下。

(一)涡流蔓延项(A) A＝2λdp (8-17) 涡流蔓延项也称多流路效应项。

它与填充物的平均颗粒直径dp有关，也与填充不匀称因子λ有关，即填充愈匀称、颗粒愈小，则塔板高度愈小、柱效愈高。

涡流蔓延的方向垂直于载气流淌方向，所以也称径向蔓延或多路效应。

它与载气的性质、线速度、组分的性质、固定液用量无关。

但是当填充物颗粒大小不一，且颗粒粗壮，填充又不匀称，则会造成色谱峰形扩展，8-43。

图8-43 涡流蔓延引起峰形扩展暗示图图中三个起点相同的组分，因为在柱中通过的路径长短不一，结果三个质点不同时流精彩谱柱，造成了色谱峰的扩展。

(二)分子蔓延项(B/u) B＝2γDg (8-18) B称分子蔓延系数，它与组分在气相中的蔓延系数Dg,填充柱的弯曲因子γ有关。

对于空心柱γ=1，对于填充柱，因为颗粒使蔓延路径弯曲，所以γ 1，常用硅藻土载体γ=0.5～0.7。

分子蔓延也叫纵向蔓延，这是基于载气携带样品进入色谱柱后，样品组分形成浓差梯度，因此产生浓差蔓延，因为沿轴向蔓延，故称纵向蔓延(图8-44)。

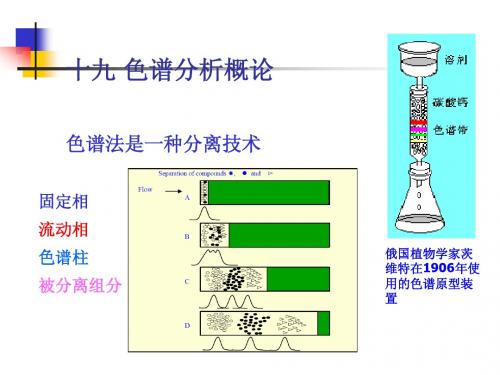
第18章　色谱法导论18-1 试说明分离的含义及热力学限制、分析分离与制备分离的区别与联系。

答：（1）分离的含义及热力学限制①含义。

分离（separation）是指利用混合物中各组分在物理性质或化学性质上的差异，通过适当的装置或方法，使各组分分配至不同的空间区域或在不同的时间依次分配至同一空间区域的过程。

②热力学限制。

由热力学第二定律可知，混合是一个熵增的自发过程，稀释或分子离散都是熵增加的自发过程，而分离和浓缩过程熵值减小，必须要外加能量，或者说必须做功才能完成，这是分离的热力学限制。

（2）分析分离与制备分离的区别与联系g①由于色谱分析所需试样量少，试样用量量级一般在mg、级别甚至更少，可测定混合物中含量极低的痕量成分，分析分离常在极微小体系内完成，如毛细管、芯片式的微通道。

②与分析分离相比，制备分离处理试样的量级在mg至g级范围，它们分离的目的也不完全相同。

18-2 什么是色谱分离？色谱过程中试样各组分的差速迁移和同组分分子离散分别取决于何种因素？答：（1）色谱分离是指基于不同物质在由固定相和流动相构成的体系中具有不同的分配系数，在采用流动相洗脱过程中呈现不同保留时间，从而实现分离的技术。

（2）色谱过程中试样各组分的差速迁移和同组分分子离散分别取决于组分和溶质与固定相作用力差异，与组分在两相中分布常数有关。

分布常数大小则由组分或溶质、固定相、流动相分子结构及作用力的差别有关。

18-3 色谱热力学、色谱动力学研究的对象是什么？它们有什么区别与联系？在色谱条件选择上有何实用价值？答：（1）色谱热力学研究的对象是分子结构与色谱保留值的关系及溶质在各种色谱条件下保留值的变化规律，色谱动力学研究的对象是色谱过程流体分子运动规律。

（2），色谱热力学与色谱动力学的区别与联系：色谱热力学是发展高选择性色谱体系，特别是研发色谱固定相，探讨色谱分离机理，评价色谱固定相、流动相，建立色谱定性方法的理论基础。

色谱动力学是发展高效色谱柱材料、柱技术和色谱方法的理论基础。