当前位置：文档之家 › 结构动力学(运动方程)

结构动力学(运动方程)

  • 格式：ppt
  • 大小：2.41 MB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

结构动力学第二章 运动方程的建立

结构动力学第二章 运动方程的建立

h—框架结构的高度 E—弹性模量 Ib和Ic—梁和柱的截面惯性矩
ρ→∞：
k
24EIc h3
ρ→0
：
k
6EIc h3
2.1 基本动力体系
3. 阻尼力（Damping Force）
阻尼：引起结构能量的耗散，使结构振幅逐渐变小的一种作用 阻尼来源（物理机制）： (1)固体材料变形时的内摩擦，或材料快速应变引起的热耗散； (2)结构连接部位的摩擦，结构构件与非结构构件之间的摩擦； (3)结构周围外部介质引起的阻尼。例如，空气、流体等。
非保守力做功的变分等于0。
t2 (T V )dt t2 Wncdt 0
t1
t1
Wnc Pncju j
j
其中：
T —— 体系的总动能； V —— 体系的位能，包括应变能及任何保守力的势能； Wnc—— 作用于体系上非保守力（包括阻尼力及任意外荷载）所做的功； δ —— 指（在指定时间段内）所取的变分。
p(t) fI fD fs 0 fI mu fD cu fs ku
mu cu ku p(t)
图2.8 单质点体系的受力分析
2.2 运动方程的建立
3. 虚位移原理
虚位移原理的优点：虚位移原理是建立在对虚功分析的基础之 上，而虚功是一个标量，可以按代数方式运算，因 而比Newton第二定律，或D’Alembert原理中需要采 用的矢量运算更简便。
对如下图所示结构体系，用虚位移原理建立方程更简便一些
2.2 运动方程的建立
4. Hamilton原理
应用变分法来建立结构体系的运动方程。 动力学中广泛应用的变分法是Hamilton原理 体系的平衡位置是体系的稳定位置，在稳定位置，体系的能量取得极值, 一般是极小值。

结构动力学

结构动力学

第2章 单自由度系统
§2.4 简谐荷载的强迫振动
2.4.1 无阻尼系统
1、运动方程
mx kx F0 sin t
2、解的形式
x x x
设：
x A sin t
(m 2 k ) A F0
第2章 单自由度系统
解得：
A
A
(m 2 k )
F0 k xst (1 2 2 ) (1 2 )
已知
结构
荷载
响应
荷载
已知或未知
结构
已知
第1章 绪论
§1.2 研究对象
1、结构——弹性恢复力 fk(x) 2、外力——时变特性 fp(t)
§1.3 研究内容
1、结构动力特性——固有频率、振型、阻尼 2、结构响应——位移、速度、加速度
第1章 绪论
§1.4 研究方法
1、时域法——解析法、逐步积分法 2、频域法——谱分析法

k m
①简支梁问题
m l
第2章 单自由度系统
1 k
l3 48 EI
k
48EI l3
48EI ml 3

第2章 单自由度系统
②悬臂梁问题 弯曲变形
x

l 3EI
3
m
k
3EI l3
k
剪切变形
l3 12EI
k
12EI l3
弯曲变形 剪切变形
第2章 单自由度系统

2 i i ,max m xi ki xi2,maxi
第2章 单自由度系统
m x
i 2 i i ,max
2 2 J max m2 xmax
1 2 2 m1l 2 max m2l 2 max 3 1 2 m1l 2 m2l 2 max 3

结构动力学_运动控制方程_分段解析法

结构动力学_运动控制方程_分段解析法

结构动力学运动控制方程分段解析法1. 引言1.1 概述在工程领域中，结构动力学是研究结构物体受外界力或激励下的响应和振动特性的一门学科。

结构动力学广泛应用于建筑、桥梁、飞机等领域，对于确保结构物的安全性和稳定性具有重要意义。

随着现代科技的发展，运动控制方程在结构动力学中扮演着至关重要的角色。

通过运动控制方程，我们可以深入理解和预测结构物运动的规律，并为其设计合适的控制策略。

因此，研究和解析这些方程是结构动力学研究中必不可少的一部分。

1.2 文章结构本文将按照以下顺序进行组织和阐述：首先，在第二部分中，我们将简要介绍结构动力学的定义和原理，以及涉及到的动力学方程。

接着，在第三部分中，我们将详细介绍分段解析法作为一种常见的求解方法，包括其基本原理、算法步骤以及相关应用案例。

在第四部分中，我们将描述所设计实验的参数设置，并对实验结果进行分析和讨论。

最后，在第五部分中，我们将总结本文的主要结论，并展望未来研究方向。

1.3 目的本文的主要目的是通过对结构动力学和运动控制方程的介绍，以及分段解析法的应用案例分析，进一步加深对相关理论和方法的理解。

同时，希望为研究者提供一个清晰、系统的框架，以便于更好地理解和应用这些内容。

鉴于分段解析法在结构动力学领域具有广泛应用和良好效果，本文还旨在为读者提供相关方法在实际工程问题中的指导参考。

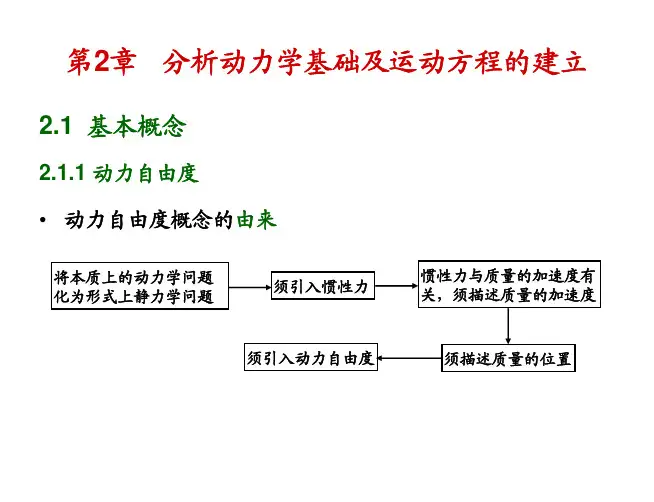
2. 结构动力学2.1 定义和原理结构动力学是一门研究物体在受到外部力作用下的运动规律的领域。

它主要涉及质点的运动学和动力学，以及刚体与弹性体的运动特性。

在结构工程中，结构动力学用于分析和预测建筑物、桥梁、飞机等工程结构在自然环境或人为作用下的响应情况，并提供相应的设计依据。

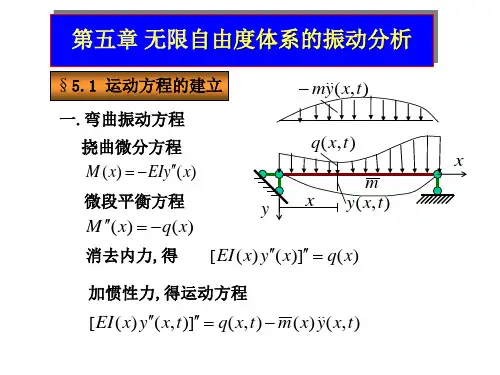
2.2 动力学方程结构动力学理论通过牛顿定律和哈密顿原理等基本原理推导出结构系统的运动方程。

这些方程描述了结构物各个部分之间的相互关系，并包括质量、刚度、阻尼等参数。

根据实际工程问题，可以选择合适的数值解法求解这些方程，从而得到结构系统随时间变化的运动状态。

结构动力学4

结构动力学4
2
4.2 有阻尼体系的简谐振动
通解uc对应于有阻尼自由振动反应：
u c (t ) = e
−ζω n t
( A cos ω D t + B sin ω D t )
特解up可以设为如下形式 :
u p (t ) = C sin ωt + D cos ωt
p0 && & u + 2ζω n u + ω n u = sin ωt m
1 − (ω / ω n ) 2 C = u st [1 − (ω / ω n ) 2 ]2 + [2ζ (ω / ω n )]2 − 2ζω / ω n D = u st [1 − (ω / ω n ) 2 ]2 + [2ζ (ω / ω n )]2
运动方程的全解：u(t)=uc+up ：
u(t ) = e
u (t ) = C sin ωt + D cos ωt = u 0 sin(ωt − ϕ )
u0 —稳态振动的振幅 φ —相角，反映体系振动位移与简谐荷载的相位关系
D 2 2 −1 u 0 = C + D , ϕ = tan (− ) C
u 0 = u st 1 [1 − (ω / ω n ) 2 ] 2 + [ 2ζ (ω / ω n )] 2
uc (t ) = A cos ωn t + B sin ωn t
ωn = k / m
c - complementary
4.1 无阻尼体系的简谐振动
&& mu + ku = p 0 sin ωt
特解—满足运动方程的解，记为up(t) ，是由动 荷载p0sinωt直接引起的振动解。 设特解为：u p (t ) = C sin ωt + D cos ωt

结构动力学第二章

结构动力学第二章

∂T ∂V d ∂T ( )− + = Pncj (t ), & dt ∂u j ∂u j ∂u j
其中： T —— 体系的动能；
j = 1,2,L , N
V —— 体系的位能，包括应变能及任何保守力的势能； Pncj ——与 uj 相应的非保守力（包括阻尼力及任意外荷载）。
– 红色部分为引入动力自由度概念的目的，蓝色部分为实 现此目的的手段。 – 概念中的“全部”、“独立”两个条件非常关键。
• 严格来说，所以结构体系质量都是连续分布的，为无限自 由度体系，研究比较困难。但许多情况下，可以作一定的 简化，变为有限自由度体系。 • 简化并确定结构动力自由度最典型的方法：集中质量法
动能
1 & mu 2 转动质量 2
T =
1 &2 Jθ 2
1 2 V = ku 转动弹簧 2
1 &2 V = kθ θ 2
位能
1 1 & & &j T = ∑ ∑ mij u i u j = ∑ m j u 2 2 i j 2 j
V =
1 ∑ ∑ kij ui u j 2 i j
∫
1 体系的动能：T = mu 2 & 2
粘滞(性)阻尼力可表示为：
& f D = -cu
D — 表示阻尼（damping） c — 阻尼系数（Damping coefficient）
k c
u m
f S(t) m f D(t) f I (t)
& u — 质点的运动速度
阻尼系数 c 的确定：
• 不能像结构刚度 k 那样可通过结构几何尺寸、构件尺寸等 来获得，因为 c 是反映了多种耗能因素综合影响的系数， 阻尼系数一般是通过结构原型振动试验的方法得到。 • 粘性（滞）阻尼理论仅是多种阻尼中最为简单的一种。 • 其它常用的阻尼：

结构动力学方程及有限元方程

结构动力学方程及有限元方程

，则：
• 方程的通解为：
• 则n 自由度无阻尼系统受迫振动广义坐标下的稳态响应为：
上一页
返回
8.5 复杂系统动力学模型
• 对于复杂机械系统多用拉格朗日法研究其动力学模型，在广义坐标、 功和能的基础上建立微分方程，即：
• 式中 T ——系统动能； • U ——系统势能； • D ——虚功； • j Q′ ——广义势力； • j q ——系统广义坐标。
8.2 单元特性矩阵
• 其单元质量矩阵[M]为2× 2阶矩阵。其集中质量矩阵为：m =W / g = ρ Al ，载荷均匀分布，节点i和节点 j各承担m / 2。则有：
• 杆单元的形函数矩阵为：
上一页 下一页 返回
8.2 单元特性矩阵
• 则杆单元的一致质量矩阵为： • （2）三角形平面单元的一致质量矩阵为：
的微分方程的求解问题，式（8.72）则可以写为：
上一页 下一页 返回
8.4 振动系统响应分析
• 利用单自由度的概念和方法，可得到稳态响应为： • hr（ t） 为第r 阶模态的脉冲响应函数，则： • 代入整理得：
上一页 下一页 返回
8.4 振动系统响应分析
• 系统施加的初始条件为{δ (0)}和
上一页 下一页 返回
8.3 固有特性分析
• 将解代入振动方程中，同时消去因子e jω t ，得：
• 系统的固有频率和振型是结构固有的特性，它仅与结构的质量和刚度 有关，而与外界影响无关。外界扰动只能影响振幅，不能改变其固有
频率，若要改变结构的固有频率，只能从改变结构的质量或刚度入手， 固有频率是结构动力性能的一个重要标志。
8.4 振动系统响应分析
• 则n 自由度无阻尼系统自由振动广义坐标下的稳态响应为：

结构的动力学方程

结构的动力学方程()g MX CX KX MIx t ++=-clear; clc; n=4;II=sqrt(-1);%主结构质量、阻尼、刚度矩阵123400000000000m mM m m ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦M=eye(n)*1.0e+4; K=eye(n)*1.6*1.0e+7; %主结构刚度矩阵聚合 zk=zeros(n);122223333444400000k k k kk k k K k k k k k k +-⎡⎤⎢⎥-+-⎢⎥=⎢⎥-+-⎢⎥-⎣⎦for j=1:(n-1)zk(j,j)=K(j,j)+K(j+1,j+1); zk(j,j+1)=-K(j+1,j+1); zk(j+1,j)=-K(j+1,j+1); endzk(n,n)=K(n,n); k=zk; m=M;%求解各阶模态频率 [tzxl,tzz]=eig(k,m); d=diag(sqrt(tzz)); %振型规一化 for i=1:n[tzz1(i),j]=min(d); tzxl1(:,i)=tzxl(:,j); d(j)=max(d)+1; end%振型归一化取第一层振型为1 for j=1:ntzxl1(:,j)=tzxl1(:,j)/tzxl1(1,j); endw0=tzz1;w=tzz1/(2*pi); zhx=tzxl1;广义阻尼矩阵1112220333444200002000020002M M C M M ζωζωζωζω⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦各阶模态阻尼比都取0.05i ζ= %阻尼比ks0=0.05;ks=ones(n,1)*ks0;第n 阶广义质量：Tn n n M M φφ=%求广义质量 Mn=zhx'*m*zhx; 阻尼矩阵为：()()110TC C φφ--=%求阻尼矩阵 C=zeros(n); for i=1:nC(i,i)=2*ks(i)*w0(i)*Mn(i,i); endc=(zhx')\C/zhx;()()4222022222244g g g g x g g gS S ωζωωωωωζωω+=-+参数eg 即g ζ%过滤白噪声参数 eg=0.6; wg=15.708; S0=0.001574;%按照书上的要求，取频率和时间的最大值和步长 %频率间隔 dw=0.3;%最大频率范围 maxw=45; %最大时间值 maxt=40; %时间间隔 dt=0.2;%各层各时间点频率点的功率谱密度,循环变量：层数，时间点，频率点 Pwt=zeros(n,maxt/dt,maxw/dw); %频率点数循环变量wn wn=1;%对频率进行循环，求解各频率点的时间历程 for w=0:dw:maxwx1=1+4*eg^2*(w/wg)^2;x2=(1-(w/wg)^2)^2+4*eg^2*(w/wg)^2; Sgw=x1*S0/x2; s=sqrt(Sgw);%采用精细积分法进行求解时间历程，得到位移和速度时程 [disp,velp]=JINGXI67(M,zk,c,dt,maxt,w,s,n); Ywt=disp;for kkk=1:maxt/dt%求确定频率下各时间点的功率谱 Yw=Ywt(:,kkk);()()()()()1234t t t t t y y y y y ωωωωω⎧⎫⎪⎪⎪⎪=⎨⎬⎪⎪⎪⎪⎩⎭每一时刻和频率点的位移向量，对其进行求共轭和装置得到协方差矩阵，对角上的元素即是每一时刻的各层的功率谱y1=conj(Yw);y2=transpose(Yw);()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()11121314212223243132333441424344t t t t t t t t t t t t t t t t yy t t t t t t t t t t t t t t t t y y y y y y y y y y y y y y y y S y y y y y y y y y y y y y y y y ωωωωωωωωωωωωωωωωωωωωωωωωωωωωωωωωω****************⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ %确定时间点确定频率下的功率谱Yw,取对角线元素Syyw=y1*y2; for kk=1:nPwt(kk,kkk,wn)=Syyw(kk,kk); end endwn=wn+1; end()()()()()()()()()()()()()()2012311231212222yyy yy yy yy n yy yy yy n yy yy n yy yy yy n S d S d S S S S S d S S S S S d σωωωωωωωωωωωωωωωω+∞+∞-∞--==⎡⎤ =⨯++++⋯+⎣⎦⎡⎤ =++++⋯+⎣⎦⎰⎰ %求解完成后实际上wn 为maxw/dw+2，实际频率点个数为maxw/dw+1%各层的时变方差，循环变量为：层数，时间点 Fangcha=zeros(n,maxt/dt); for tn=1:maxt/dt%求解各层的时变方差 for kk=1:nxx1=zeros(wn-1,1);%每一个时刻的方差对各频率点进行积分，频率点数取maxw/dw+1，即wn-1 for wn0=1:wn-1xx1(wn0)=Pwt(kk,tn,wn0); end%采用复合梯形求积公式对功率谱进行积分得到方差Fangcha(kk,tn)=(xx1(1)+xx1(wn-1)+2*sum(xx1(2:wn-1-1)))*dw; end end%画图c1=(1:maxt/dt)*dt; d1=Fangcha(1,:)/S0; d2=Fangcha(2,:)/S0; d3=Fangcha(3,:)/S0; d4=Fangcha(4,:)/S0; figure(3)plot(c1,d1,'k',c1,d2,'r',c1,d3,'m',c1,d4,'r-')精细积分的程序function [disp,velp]=JINGXI67(m,k,c,dt,maxt,w,s,n) %虚数单位 II=sqrt(-1); % i teω中的i ωIIW=II*w; I=eye(n); Z=zeros(n);离散化n 自由度结构受均匀调制演变随机激励(){}f t 时的运动微分方程可表示为：()()()My Cy Ky f t MIg t x t ++==-其中()x t 为平稳高斯白噪声随机过程向量，()g t 为调制函数。

【结构动力学】第1章 运动方程 2020

12
承受动力荷载的任何线性结构体系的主要物理特性是体系的质量、弹 性特性（刚度或柔度）、能量耗散机理或阻尼、以及外部扰力或荷载
单自由度
c
体系模型
k
y (t )
F(t) m
▪ 质量块m，用来表示结构的质量和惯性特性 ▪ 自由度只有一个：水平位移 y(t) ▪ 无重弹簧，刚度为 k，提供结构的弹性恢复力 ▪ 无重阻尼器，阻尼系数c，表示结构的能量耗散，提供结
y P (FI FD )
改写成：
FI
FD
1
y
P
28
位移方程：
FI
FD

1
y
P
其中：
p为动荷载 q(t) 引起的质量沿y方向的位移：
q (t)y(t )
P
5l 4 384 EI
q(t )
惯性力： FI my 阻尼力： FD cy
为自由度方向加单位力所引起的位移，即柔度： 由此得到体系的运动方程：
my cy ky F(t) (2-3)
y(t )
EI l 1
my
cy
12EI
l13
12EI l23
y
FP (t)
12EI 12EI
令： k FS1 FS 2 l13 l23
；k 为（等效）刚度系数。
由此得到体系的运动方程： my cy ky FP (t)
运动方程与(2-3)的形式是一样的！
my cy ky F(t)
（2-3）
14
直接平衡法(达朗贝尔原理)
直接平衡法，又称动静法，将动力学问题转化为任 一时刻的静力学问题：根据达朗贝尔原理，把惯性 力作为附加的虚拟力，并考虑阻尼力、弹性力和作 用在结构上的外荷载，使体系处于动力平衡条件， 按照静力学中建立平衡方程的思路，直接写出运动 方程。

结构动力学-第一章

1，集中质量法 2，广义坐标法 3，有限单元法
2019/9/16
38
2019/9/16
39
2019/9/16
40
2019/9/16
41
2019/9/16
42
2019/9/16
43
三. 自由度的确定
广义坐标法：广义坐标个数即为自由度个数； 有限元法：独立结点位移数即为自由度数； 集中质量法：独立质量位移数即为自由度数；
11

l3 3EI
柔度系数
my(t) 3 EI l3y( Nhomakorabea)
P(t)
2019/9/16
柔度法步骤： 1.在质量上沿位移正向加惯性力； 2.求外力和惯性力引起的位移； 3.令该位移等于体系位移。
49
二、刚度法
P(t)
m
1
my(t)
y(t)
l EI
y
k11
k11 y(t )
k11y(t) P(t) my(t)
变分法（Hamilton原理）以及lagrange等。
我们这节课主要介绍达朗泊尔原理建立的动力学微分方程，用能量法建立 微分方程的方法在以后的章节中介绍。
达朗泊尔原理
质点系运动的任意瞬时，除了实际作用于每个质点的主动力和约束反力外， 在加上假象的惯性力，则在该瞬时质点系处于假象的平衡状态。
m P(t) my(t)
结构动力学
2019/9/16
1/
思考问题
1，结构动力学和静力学的区别和联系在哪里？
运动方程为：
m y(t) c y(t) k y(t) p(t)
静力学方程为：
k y p
201所9/9/以16 两者的区别在于：动力学问题多了惯性力项以及由运动产生的阻尼力。 2

【结构动力学】第10章 多自由度体系2020


0
0
N
其中，ωn— 第n阶自振频率，{φ}n—第 n阶振型。
[Φ]和[Ω]也分别称为振型矩阵和谱矩阵。
13
5 DOF with uniform mass and stiffness
5 DOF Base Isolated 14
15
5 DOF with uniform mass and stiffness
k22 2m22 k2N 2m2n 0
k N1 2mN1 k N 2 2mN 2 k NN 2mNN
10
对于N个自由度的稳定结构体系，频率方程是关于ω2的 N次方程，
a N ( 2 ) N a N 1 ( 2 ) N 1 a1 2 a 0 0
由此可以解得N个正实根（ω12<ω22<ω32…<ωN2）。 ωn(n=1, 2, …, N)即为体系的自振频率。其中量值最小的 频率ω1叫基本频率(相应的周期T1=2π/ω1叫基本周期)。 从以上分析可知，多自由度体系只能按一些特定的频 率即按自振频率做自由振动。按某一自振频率振动时，结 构将保持一固定的形状，称为自振振型，或简称振型。
上述齐次方程组有非零解条件为：系数行列式为零
A [I ] 0
N×N矩阵[A]一般将有N个特征值，对应N个特征向量
6
§10-2 多自由度体系的自由振动
多自由度体系无阻尼自由振动的方程为：
M u K u 0
其中：[M]、[K]为N×N阶的质量和刚度矩阵 {u}和{ü}是N阶位移和加速度向量 {0}是N阶零向量
11
把相应的自振频率ωn代入运动方程的特征方程得到振型
K n 2 M n 0
{φ}n={φ1n, φ2n , …, φNn }T—体系的第n阶振型 。 ➢ 由于特征方程的齐次性(线性方程组是线性相关的)，振型向量 是不定的，只有人为给定向量中的某一值，例如令φ1n=1，才能确 定其余的值。 ➢ 实际求解时就是令振型向量中的某一分量取定值后才能求解。 虽然令不同的分量等于不同的量，得到的振型在量值上会不一样， 但其比例关系是不变的。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
mv cv ku Peq(t )
•式中：m质量；c阻尼系数；k刚度系数；Peq为等效 动荷载。 • 当动荷载直接作用在质量上时，Peq为动荷载的合 力在运动方向的投影； • 当动荷载不作用在质量上时，Peq为动荷载作用下 限制沿自由度运动的支座反力。
• 用刚度法还是用柔度法建立方程，看具体问题是 求刚度系数方便、还是求柔度系数方便来定。 • 没有等效动荷为自由振动，没第二项为无阻尼振 动
p(t)
m
d
2u(t) dt 2
mu&&(t)
3.2.1.1-2
式中： mu(t) 称为抵抗质量加速度的惯性力。
直接平衡法
通过动力体系各质点的力矢量平衡关系建立运动方程 的方法。质量所产生的惯性力与它的加速度成正比，但方 向相反。这一概念称为达兰贝尔原理。借助该原理可以把 运动方程表示为动力平衡方程。方程中的力包括多种作用 于质量上的力，如抵抗位移的弹性恢复力、抵抗速度的粘 滞阻尼力以及其它独立确定的外荷载。因此，运动方程的 表达式仅仅是作用于质量上所有力（包含惯性力）的平衡 表达式。在许多简单问题中，直接平衡法是建立运动方程 的最直接而且方便的方法。
对称振动。设质量竖向位移为v，向下为正。
• 利用对称性由（形常数）可得质量 点处所加支杆单位位移时的R（=？）。
•1•R
以m为隔离体，加上惯性力fI、阻尼力fd 如图所示，根据达朗泊尔原理和阻尼假
•fI+ fd
•R
定
fI mv fd cv
•R •P(t)
•因此由所示“外力”平衡可得•显然,整理後结果和例-2)
•2.1 建立运动方程的基本步骤
• 作为本科学习，这里只讨论用达朗泊尔原理通过
列平衡方程得•列到运位动移方方程的程“称直柔接度平衡法法”。以下讨
论中一律认为系统的阻尼是等效粘滞阻尼。 • 直接平衡法列方程的一般步骤为： • 1) 确定体系的自由度——质量独立位移数； • 2) 建立坐标系，确定未知位移（坐标正向为正）； • 3) 根据阻尼理论确定质量所受的阻尼力； • 4) 根据达朗泊尔原理在质量上假想作用有惯性力 （注意：惯性力是实际的，但它不作用在质量上）；
如图 3.2.1.1（b）所示，根据力的平衡可以得：
fI fD fS p(t) 即
3.2.1.1-3
mu&& cu& ku p(t)
3.2.1.1-4
公式 3.2.1.1-4 即为单自由度体系运动方程。
虚位移原理
虚位移原理可表述为：如果一组力作用下的平衡体系 承受一个虚位移（即体系约束所允许的任何微小位移）， 则这些力所作的总功（虚功）等于零，虚功为零和体系平 衡是等价的。因此，只要明了作用于体系质量上的全部力 （包括按照达兰贝尔原理所定义的惯性力），然后引入对 应每个自由度的虚位移，并使全部力作的功等于零，则可 导出运动方程。虚功为标量，故可依代数方法相加，这是 此法的主要优点。
• 5) 将动力外荷、惯性力、阻尼力作为“外力”， 按位移计算公式求各质量沿自由度方向的位移，其结 果应该等于未知位移（满足协调），由此建立方程。
•2.2 运动方程建立举例
•2.2.1 单自由度体系运动方程
•例-1) 试建立图示结构的运动方程。 •P(t) •m •解：由于横梁刚度无穷大，结构只能产 •EI •h
mmvvccvv2kRu P(t) 相同，k= -1
•2.2 运动方程建立举例
•2.2.1 单自由度体系运动方程
•m •P(t)
•例-5) 若例-2)简支梁动荷载作用在3l/4 •l/ •l/
处,试建立其运动方程
22
•解：将惯性力fI、阻尼力fd如图所示加于•梁作上业，：根据达
朗••仅泊在由尔fPI位原(t)移7理作6计和用m8E算阻v下I可尼mP知的假，位f定1d单移1P位由(荷位tc)v载l移3 下计简算支得梁•••物是跨P理什•2中l/•竖意麽f-I1的向义？••2f位ld/•P(t)
牛顿第二运动定律
任何质量 m 的动量变化率等于作用在这个质量上的力。这一关系在
数学上可用微分方程来表达：
p(t) d (m du(t)) dt dt
3.2.1.1-1
式中： p(t) 为作用力矢量；u(t) 为质量 m 的位移矢量。对于大多数的结
构动力学问题，可以假设质量不随时间变化，这时方程（1）可改写作
•因此，外力下位移为
理後结果和 例-1）相同，
k= -1
•1
•h
M1
u (P(t) mu cu)
•2.2 运动方程建立举例
•2.2.1 单自由度体系运动方程
•m•P(t)
•例-4) 试建立图示抗弯刚度为 EI 简支梁 •l/ •l/
的运动方程。（不计轴向变形）
22
•解：图示结构只能产生竖向位移，显然这是单自由度
利用关系 δu& d(δu) / dt ，上式中的第一项可表示为如下的分部积分：
t2 mu&δu&dt mu&δu t2 t2 mu&&δudt
t1
t1
t1
3.2.1.3-3
哈密尔顿原理假定变分 u 在积分限 t1 和 t2 时为零，故方程 3.2.1.3-3 右边第一项为
零，将上式代回方程 3.2.1.3-2，结果为
例：由刚体质量、支承弹簧与阻尼器组成的单自由度体系如图所示，刚体仅可 作单一方向运动。
x x
(a) 物理模型
(b) 平衡力系
图 3.2.1.1 理想化单自由度运动体系
图中 k 为弹簧刚度， m 为质量， c 为阻尼系数， p(t) 为外力。若 u 、 u&、 u&&分
别为体系的位移、速度和加速度反应，则质量块承受的惯性作用 fI mu&&，弹性恢 复力 fS ku ，粘滞阻尼力 fD cu&。
•
•例-3) 试建立图示结构的运动方程。 •P(t) •m
•解：由于横梁刚度无穷大，结构只能
•EI •h
产生水平位移。设质量m位移为u，向
右为正。根据达朗泊尔原理和假设的 •P(t) muu
阻尼力理论，加惯性力和阻尼力后受
力• 如由图超。静定位移计算可得（•显如然图，示整意） cu •h
h3
24EI
复力fef。I 根 据m达u朗泊尔原fd理和阻cu尼假定fe
•f
eБайду номын сангаас•m
•f
d
•fI
ku
•P(t)
•因此由所示“外力”平衡可得
mv cv ku P(t)
• 由这些例子显然可见，不管什麽单自由度结构，
运动方程的最终形式都是一样的。
•2.2 运动方程建立举例
•单自由度体系运动方程建立小结
• 任何单自由度结构，运动方程都可写为
•2.2 运动方程建立举例
•2.2.1 单自由度体系运动方程
•m•P(t)
•例-2) 试建立图示抗弯刚度为 EI 简支梁 •l/ •l/
的运动方程。（不计轴向变形）
22
•解：图示结构只能产生竖向位移，显然这是单自由度
对称振动。设质量竖向位移为v，向下为正。 •fd
• 将惯性力fI、阻尼力fd如图所示加于
t2 δ(T V )dt t1
t2 t1
δWncdt
0
3.2.1.3-1
式中：T 为体系的总动能；V 为体系的位能，包括应变能及任何保守外力（如 重力）的势能；Wnc 为作用于体系的非保守力（包括阻尼力及任意外荷载） 所作的功；δ 为在指定时间区间内所取的变分。哈密尔顿原理表明在任何时
间区间 t1 ~ t2 内，动能和位能的变分与非保守力所作的功的变分之和必须等
生水平位移。设x坐标向右（右手系）。
• 又设横梁（质量m）位移为u，以它 为隔离体，受力如图所示。
•P(t)
mu
• 图中Fs1和Fs2可由图是有位移法（实 Fs1 cuFs2
际直接可由形常数）得到
Fs1
Fms2u1c2huE3I
kuukPu(t 2
)
uu
•h
•列x方向全部力的平衡方程，即可得结
构的运动方程为
结构动力学
张系斌
2015.5.
•二、体系的运动方程建立
• • 2.1 建立运动方程的基本步骤 • • 2.2 运动方程建立举例
• 2.3 体系运动方程的一般形式 • 2.4 应注意的几个问题
• 2.5 刚度法、柔度法列方程的步骤 • • 2.6 运动方程建立总结
运动方程的建立
建立动力体系运动方程常用的三种方法是直接 平衡法、虚位移原理方法和哈密尔顿原理方法；运 动方程可用上述三种方法中的任一种建立。对于简 单体系，最明了的方法是采用直接平衡法建立包括 惯性力在内的作用于体系上的全部力的平衡关系， 得出运动方程。对于更复杂的体系，直接建立矢量 平衡关系可能是困难的，此时采用功和能等标量建 立平衡关系更为方便；其中包括虚位移原理方法和 哈密尔顿原理方法。上述三种方法的结果是完全相 同的，采用何种方法取决于是否方便、个人的喜好 以及动力体系的性质。
当结构体系相当复杂，且包含许多彼此联系的质量点 或有限尺寸的质量块时，直接写出作用于体系上的所有力 的平衡方程可能是困难的；尽管作用于体系的力可以容易 地用位移自由度来表示，但它们的平衡关系则可能十分复 杂。此时，利用虚位移原理建立运动方程更为方便。
例：假设给图 3.2.1.1（b）所示体系一个虚位移u （仅仅 是体系约束所允许的微小位移），则作用于体系的全部力都将做 功，体系所作的总功可写作
•fI
梁上，根据达朗泊尔原理和阻尼假定
•l/ •l/
fI mv fd cv
2 •P(t2)
• 由位移计算可知，单位荷载下简支梁跨中竖向位