简谐运动的动力学方程共34页

动的依据） 2.对称性——简谐振动物体具有对平衡位置的对称
性，在关于平衡位置对称的两个位置，动能、势 能相等，位移、回复力、加速度大小相等，方向 相反,速度大小相等，方向可能相同，也可能相 反,振动过程相对平衡位置两侧的最大位移值相等.
3.周期性——简谐运动的物体经过相同时间t=nT(n) 为整数,必回复到原来的状态,经时间t=(2n+1) T2 (n为整数)，则物体所处的位置必与原来的位置 关于平衡位置对称，因此在处理实际问题中，
图2 3.简谐运动的能量
简谐运动过程中动能和势能相互转化，机械能 守恒，振动能量与 振幅 有关， 振幅 越大， 能量越大.
二、简谐运动的两种基本模型
弹簧振子（水 平）
单摆
模型示意图
条件 平衡位置
回复力
忽略弹簧质量、 无摩擦等阻力
细线不可伸长、质量 忽略、无空气等阻力、 摆角很小
弹簧处于原长处
最低点
度方向上的力充当向心力，即F向=F-mgcosθ；摆 球重力在平行于速度方向上的分力充当摆球的回复
力.当单摆做小角度摆动时，由于F回=-mgsinθ= - mg x=-kx，所以单摆的振动近似为简谐运动.
l
3.单摆的周期公式 (1)单摆振动的周期公式T=2π l ,该公式提供了
g
一种测定重力加速度g的方法. (2)l为等效摆长,表示从悬点到摆球重心的距离, 要区分摆长和摆线长，悬点实质为摆球摆动所在
2. 简谐运动的描述 （1）描述简谐运动的物理量 ①位移x：由平衡位置指向振动质点所在位置的 有向线段表示振动位移，是矢量. ②振幅A：振动物体离开平衡位置的最大距离， 是标量，表示振动的强弱. ③周期T和频率f:做简谐运动的物体完成 一次 全振动所需要的时间叫周期，而频率则等于单 位时间内完成 全振动的次数 ；它们是表示振动 快慢的物理量.二者互为倒数关系.

23

6
1 s1
t 0
A vm 31.4 10cm
3.14
x 10 cos( t )cm
6


2
o
v
t 1s
A
x02
(v0

)2

mg k
1 2kh (m M )g
最大位移=
x0

A
mg k

mg k
1 2kh (m M )g

mg k
1
1
(m
2kh M
)g

一、简谐振动的动力学方程
小ቤተ መጻሕፍቲ ባይዱ
d2 dt
x
2


2
x

0
结
二、简谐振动的运动学方程
x Acos(t )
弹簧振子 k
m
单 摆 g
l
T 2 m
k
T 2 l
g
1 k 2 m
1 g 2 l
复 摆 mgh T 2 I 1 mgh
I
mgh
2 I
(3) 位相和初位相
x Acos(t 0 )
t 0 — 位相，决定谐振动物体的运动状态 0 是t =0时刻的位相—初位相
X
v0=-Asin>0 , sin 0 <0, 取0=3/2
x=9.810-2cos(10t+3/2) m
固有频率 1 g 1.6Hz 2 2 l
例 已知某简谐振动的 速度与时间的关系曲线 如图所示，试求其振动方程。
解：方法1 设振动方程为
x Acos(t 0 )

dυ dω f =m = ml dt dt d2θ = ml 2 dt
2
dt
dθ ω= ) dt
dθ ml 2 = −mgθ dt
dθ g + θ =0 2 dt l
2
g ω= l
l T = 2π g
动力学解决问题的思路：分析系统受力， 根据系统初始条件，解出系统在任意时刻 的状态。 简 受到回复力的作用 谐 F = −kx 运 系统的初始条件 动 x0 v0 的 系 统
m T =2 π k
运动学
描述物体在空间中的运动和其随时 间的变化的一种学问。 具体的说 位移、速度 就是描质点的位移 速度 加速度 位移 速度、加速度 及其对时间的变化关系 对时间的变化关系。 对时间的变化关系
x = A cos(ωt + ϕ ) 解析法
υ = −ω A sin( ω t + ϕ )
a = −ω 2 x
f 弹 = −kx
弹簧的弹力
准弹性力举例
总结
简谐运动 ⇔ 回复力 F = − kx 动力学计算
d2x k + x =0 2 dt m
动力学方程
k ω= m
A = x +( )
2 0
ωv ϕ = arctan( − 0 ) ωx0 l 周期公式： 单摆 T = 2π 弹簧振子
g
x0,v0
v0
2
x = Acos(ωt +ϕ)
解
d 2x + ω dt 2
2
x = 0
x = A cos( ω t + ϕ )
质点作简谐运动
⇒
受到回复力
F = − kx
的作用
受到回复力
F = −kx

t 超前、落后以<
-A1
的相位角来判断。
1
2
, 2
0
1
3
2
,
2
0
2-1>0 ，x2比x1超前 π/2 1-2>0 ，x1比x2超前 3π/2
位 移 ：x(t) Acos(t )
速 度 ：(t) Asin(t )
加 速 度 ：a(t) 2 x(t)
x、 、a
2A
A
A
x
o
-A
- A
dt
2
a(t)
d 2 x(t) dt 2
2 Acos(t
)
2 x(t)
m
加速度与位移成正比而反向
x、 、a
2A
A
A
x
o
-A
- A
- 2A
a < 0 a<0 加速
<0 >0 减速
o
x
x
>0 >0 加速
T t
>0 <0 减速
三. 描述简谐运动的特征量 x(t)=Acos( t+)
1.振幅A(amplitude) 偏离平衡位置的最大距离 其值与运动如何开始有关
波动与光学
第1章 振 动 (Vibration)
生活中观察的：摇曳的树枝、飘荡的小船， 人类发明中的：颤动的琴弦或鼓膜， 人类自身中的：声带、耳膜、心脏， 不易感觉的：传递声音的空气分子的振动、
传递温度的固体内原子的振动、 传递信息的天线中电子的振动…… 周期性过程：指不断有规律重复的过程或状态。
2.周期T (period) 振动往复一次所需时间 频率v (frequency) 单位时间内的振动次数

解 取挂上物体，物体处于平衡时的位置为 坐标原点o，向下为y 轴的正向，如图所示当物 体偏离平衡位置时它所受的合力为-ky ，因此 动力学方程为
第4章 机械振动
4–2 简谐振动的运动学
14
m
d2y dt 2
ky
令 2 k
m
则上式变为
d2y dt 2
2Leabharlann y0k o
m
y
y
物体在作简谐振动，只要求出三要素， 即可写出振动方程.
v
o 0.04
x/m
0.08
第4章 机械振动
4–2 简谐振动的运动学
32
已知 m 0.01kg, A 0.08m,T 4s
t 0, x 0.04m, v0 0 求 t 1.0s, x, F
解 A 0.08m 2π π s1
T2
t 0，x 0.04m
代入 x Acos(t )
v/ (m s-1)
v Asin(t )
vm sin(t ) -0.5vm o
t/s
-vm
第4章 机械振动
4–2 简谐振动的运动学
30
t 0, v 1 2
由矢量图得
vm
sin π
1 2
6
π or 5π
66
- vm /(m s1)
- vm 2
v/ (m s-1)
t=0
π
6
第4章 机械振动
4旋–2转简矢谐量振动Ar的与运谐动振学 动的对应关系
21
旋转矢量
r A
简谐振动 符号或表达式
模 角速度 r t=0时，A 与ox夹角 旋转周期r tr时刻，A与ox夹角
A 在ox 上的投影 r A 端点速度在ox 上的投影 r A 端点加速度在ox 上的投影

点旋以转o矢为量原A
的端点在 x轴
上的投影点的
运动为简谐运 动.
第17页/共32页
x Acos(t )
t 0
o
A
x0 x
x0 Acos
点旋以转o矢为量原A
的端点在 x轴
上的投影点的
运动为简谐运 动.
第18页/共32页
t t
o
A
t
x
x Acos(t )
点旋以转o矢为量原A
的端点在 x轴
x1
A1
cos(t
1
)
x A cos(t )
2
2
2
(t 2 ) (t 1)
2
1
第25页/共32页
2 1
0同步 x
超前
π 反相 为其它 落后
x
x
o
to
o
t
t
第26页/共32页
例 一质量为0.01 kg的物体作简谐运动，其振幅 为0.08 m，周期为4 s，起始时刻物体在x=0.04 m 处，向ox轴负方向运动（如图）.试求 （1）t=1.0 s时，物体所处的位置和所受的力；
2
0.04 π)
3
m
t 1.0 s 代入上式得
x 0.069 m
F kx m 2 x 1.70103 N
A π 3
0.08 0.04 o 0.04 0.08
x/m
第28页/共32页
（2）由起始位置运动到x = -0.04 m处所需要的最短时间.
法一 设由起始位置运动到x= -0.04 m处所需要的最短 时间为t
A cos(t π)
2
o
A
a A 2 cos(t )

简谐振动的方程
一、简谐振动的动力学方程
1.弹簧振子
l0 k
m
d2x m dt2
F
kx
A o
x
A
k 2
m
d2x k
dt 2
m
x0
d2 dt
x
2
2
x
0
(1)
2 单摆
sin
(ml
2
)
d2
dt 2
M mgl
d2
dt 2
g l
0
(2)
记 2 g x
l
d2x dt 2
2x
0
(1)
O
l
T
mg
mg k
1
1
(m
2kh M
)g
一、简谐振动的动力学方程
小
d2 dt
x
2
2
x
0
结
二、简谐振动的运动学方程
x Acos(t )
t t A
t
t 0 x
o
x
x Acos(t )
旋转矢量法
初始条件确定A 初位相
例:如图m=2×10-2kg,弹簧的静止形变为l=9.8 cm. t=0 时,x0=-9.8cm,v0=0
2 描述简谐振动的特征量
(1)振幅 A
x Acos(t )
(2)周期、频率、圆频率
弹簧振子 k
m
单 摆 g
l
T 2 m
k
T 2 l
g
1 k 2 m
1 g 2 l
复 摆 mgh T 2 I 1 mgh
I
mgh
2 I
(3) 位相和初位相
x A cos(t 0 )

d2 x = ω 2 x a= 2 dt
d 2θ β = 2 = ω 2θ dt
11-2
简谐运动的动力学特征
第11章 振动学基础
二,简谐运动的能量
F = kx
x = A cos( ω t + ) v = A ω sin( ω t + )
1 2 2 E = Ek + Ep = kA ∝ A 2
d 2U 2 +ω U = 0 如:交流电压U 2 dt
ω为常数
11-2
简谐运动的动力学特征
第11章 振动学基础
2.单摆
θ <5
回复力矩
时 , sinθ
ห้องสมุดไป่ตู้
≈θ
A
M = mgl sin θ
≈ mglθ
转动 正向
θ l
FT
负号: 力矩的转向与角位移的转向相反 由转动定律: M = J β
m
o
J = ml
2
dθ mglθ = J 2 dt
2
P
11-2
dθ mglθ = J 2 dt d 2θ g = θ 2 dt l 2 dθ 2 β = 2 = ω θ dt
简谐运动的动力学特征 2
第11章 振动学基础
J = ml
2
2
g 令ω = l
与θ 成正比且反向
θ = θ m cos( ω t + )
3
x =
2
2 Ep mω
2
= 0.5 × 10 m
4
2
x = ±0.707cm
�
o
能量
xt
T
=0 t x = A cosωt v t v = Aω sin ω t

x
m
dx dt
0
式中
2 0
k m
系统固有频率
令
2m
称阻尼因子
阻尼振动方程为
d2 dt
x
2
2
dx dt
02
x
0
解 x A0et cos(t )
其中
2 0
2
第40页/共62页
2 0
2
三种阻尼振动
x
欠阻尼： 0
1.解析表达式 x Acos( t )
2.曲线描述
x
可知t 时刻质点
位置及速度方向
A
t
o
t
T
第5页/共62页
3.旋转矢量描述
用匀速圆周运动 几何地描述 简谐振动
t
逆时针转
t
A t0
-A
ox A x
矢量端点在x轴上的投影式 x Acos(t )
第6页/共62页
A
t
t=0
A
t+
o
x
x = A cos( t + )
物体做简谐振动
x0
mg kx0
o
x Acos( t ) Acos( k t )
x
m
x
思考：光滑斜面上的弹簧振子（k+m）平衡位置在何处？
是否简谐振动？若是，其w=?
第19页/共62页
3.单摆:无阻尼小角度摆动,摆长为l
平衡位置：摆球受合外力矩为零处（θ=0处）
任q角处：M合 J J m l2
第27页/共62页
3.一质点做简谐振动，其振动方程为
x
6.0
102
cos(
1 3
t

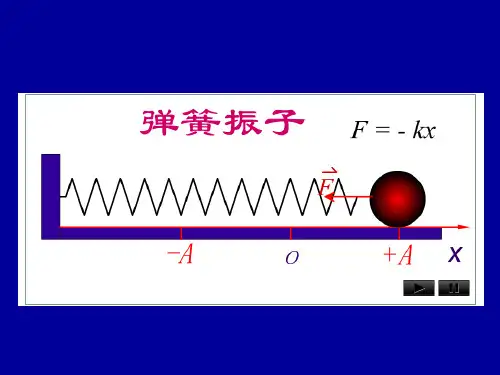
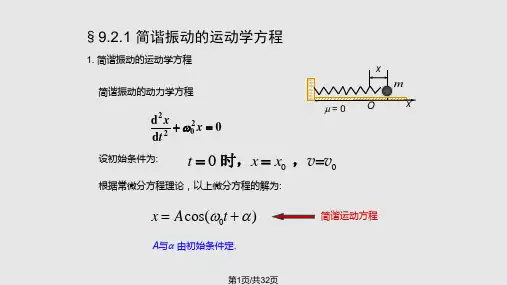
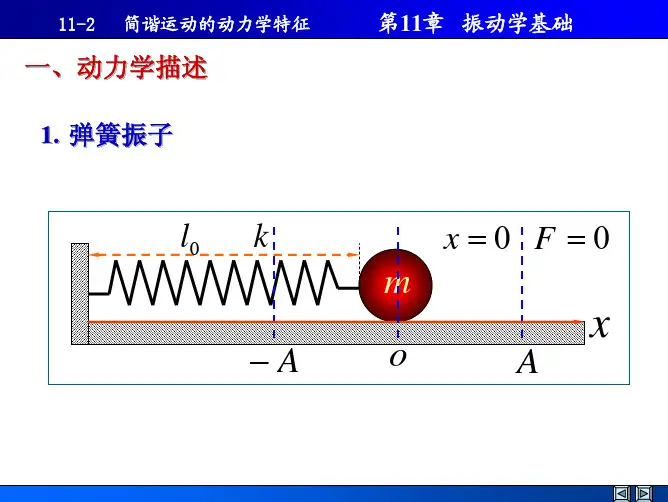
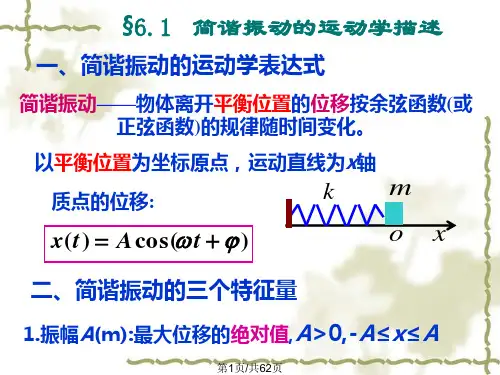
在振动过程中, 物体所受到的合外力与其相对于平衡位 置的位移成正比而反向(始终指向平衡位置), 这样的力称为 线性恢复力.
简谐运动的动力学方程
由牛顿第二定律
m d 2x kx dt2
或
d2x k x 0
dt2 m
令
2 k
m
得
d2x2 x 0
dt2
—简谐运动动力学方程
微分方程的解为 x Acos(t)
(1)单摆
如图, 细线的上端固定, 另一 端悬挂一可看作质点, 质量为 m 的重物, 细线的质量和伸长可忽 略不计. 这一振动系统叫做单摆. 重物叫做摆球, 细线叫做摆线.
若把摆球从平衡位置略为拉 开后放手, 摆球就在竖直平面内 来回摆动.
解: 规定: 右方顺时针 > 0 左方逆时针 < 0
在忽略空气阻力的情况下, 合外力沿 切线方向的分力(即重力分力) 为
它拉开一个微小角度 θ后释放. 若忽
略阻力和摩擦力, 则物体将绕轴 O作微 小的自由摆动. 这样的装置叫做复摆.
简谐运动的动力学方程
简谐运动的动力学方程
解: 复摆在力矩 M的作用下的作用下的作用下的作用下,,由
定定轴律转动定M律由m定g轴l转J动定d律2由定轴转动定律由定轴转动
dt2
动力学方程为 d2 mgl
Fτ mgsin
切向运动方程为
mgsin maτ ml
d2
dt2
即
d2 g sin 0
dt2 l
为非简谐运动.
简谐运动的动力学方程
Fτ
当θ很小时 < 50 0.0873rad sin
为简谐运动 d22
dt2
0
单摆的角频率和周期分别为

定作简谐运动。 也就是说，质点在与对平衡位 置的位移成正比而反向的合外力作用下的运动就 是简谐运动。其为简谐运动的动力学定义。
7
讨论2
得到
比较
a

d 2x dt 2

2 x
d2x dt 2

k m
x

0
简谐运动的角频率
k m
令 2 k
m
简谐运动的周期 T 2π m k
d2x dt 2
摆球的切向加速度为：
a
l
d 2
dt 2
转动
A
正向
l

FT m
o
P
9
由牛顿第二定律
ml
d 2
dt 2
mg
d 2
dt 2

g
l

0
具有
d2x k dt 2 m x 0
的形式
在角位移很小的情况下，单 摆的振动是简谐运动。
转动
A
正向
l

FT m
o
P
10
m cos(t )

2x

0
简谐运动的周期和频率仅与振动系统本身的物理 性质有关。这一周期和频率分别叫振动系统的固 有周期和固有频率。
8
2. 三个简谐振动的实例
(1) 单摆 一个质量可以忽略不 计并且不会伸缩的细线，上 端固定，下端系一可看作质 点的重物就构成一个单摆。
5 时 ,sin
Ft mg sin mg
振幅
A

2 A1 cos 2π
2
1
2
t
Amax 2 A1 Amin 0

同号时为加速 异号时为减速
O
X
A
A
第33页/共66页
振动质点位移、速度与特征点 (t=0时对应的φ)
v
xv x
x0>0时Φ在1,4象限 v0>0时Φ在3,4象限
x
v
x
第34页/共66页
x
x
xv x
例1. 一物体沿 x 轴作简谐振动，A= 12cm, T = 2s
x 当t = 0时, 0= 6cm, 且向x正方向运动。
t 时刻与x轴的夹角
( t﹢ )
相位
A
A
第32页/共66页
11
旋转矢量端续点 上M 作匀速圆周运动
其 速率
A
振子的运动速度（与 X 轴同向为正）
A
t
旋转矢量端点 M 的加速度为
法向加速度，其大小为
A
和
t
A
X O
振子的运动加速度（与 X 轴同向为正）
A
t
任一时刻的 和 值，
其正负号仅表示方向。
• 任意位置
Fmsgin
悬线的张力和重力的合力沿悬线的垂直方向指向平衡位置。
第16页/共66页
Fmsgin
当θ很小时 sinθ ≈ θ ( θ ＜ 5 °)
恢复力 Fmg
符合简谐振动的动力学定义
由牛顿第二定律
mat mg
d2
ml
mg
dt2
令 2 g l
d2 2 0
dt2
T 2 2
l g
单摆运动学方程： mcots()
弹簧振子 t= 0 时
m = 5×10 -3 kg
例三 k = 2×10 -4 N·m -1