当前位置：文档之家 › 102-简谐运动的动力学方程

102-简谐运动的动力学方程

  • 格式：doc
  • 大小：232.50 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

2021年高考复习：机械振动点点清专题3 简谐运动的公式和图像

2021年高考复习：机械振动点点清专题3 简谐运动的公式和图像

1机械振动点点清专题 3 简谐运动的公式和图像1.简谐运动的公式和图像（1）表达式①动力学表达式：F ＝－kx ，其中“－”表示回复力与位移的方向相反.②运动学表达式：x ＝A sin(ωt ＋φ0)，A 表示简谐运动的振幅，ω是一个与周期成反比、与 频率成正比的量，叫做简谐运动的“圆频率”，表示简谐运动的快慢，ω＝2π＝2πf 。

φT叫做初相，ωt ＋φ0代表简谐运动的相位。

（2）图象①从平衡位置开始计时，函数表达式为 x ＝A sin ωt ，图象如图 1 甲所示.②从最大位移处开始计时，函数表达式为 x ＝A cos ωt ，图象如图乙所示.2.简谐运动图象中可获取的信息：(1)简谐运动的图像不是振动质点的轨迹,它表示的是振动质点的位移随时间变化的规律随 时间的增加而延伸。

(2)某时刻质点的位移，振幅 A 、周期 T (或频率 f )和初相位φ0(如图 5 所示).图 5 中 t1、t2 时刻的位移分别为 x1＝7 cm ，x2＝－5 cm.图 5 中的振幅 A ＝10 cm.周期 T ＝0.2 s ，频率 f ＝1/T ＝5 Hz ，OD 、AE 、BF 的间隔都等于振动周期．图 5(3)确定质点的回复力和加速度的方向,比较它们的大小：回复力总是指向平衡位置，回复力和加速度的方向相同，在图象上总是指向 t 轴.图中 t1 时刻回复力 F1、加速度 a1 为负，t2 时刻回复力 F2、加速度 a2 为正，又因为|x1|>|x2|，所以|F1|>|F2|.|a1|>|a2|.(4)确定某时刻质点的振动方向，比较不同时刻质点的速度大小：曲线上各点切线的斜率的大小和正负分别表示各时刻质点的速度的大小和速度的方向，速度的方向也可根据下一时刻质点的位移的变化来确定.若下一时刻位移增加,振动质点的速度方向就是背离平衡位置;若下一时刻位移减小,振动质点的速度方向就是指向平衡位置。

图中的 t1、t3 时刻，质点向正方向运动；t2 时刻，质点向负方向运动．(5)某段时间内质点的位移、回复力、加速度、速度、动能和势能的大小变化情况.F＝kx――→F＝ma――→质点的位移越大，它所具有的势能越大，动能则越小，速度越小3.简谐运动的对称性：(图 6)(1)相隔Δt＝(n＋1)T(n＝0,1,2，…)的两个时刻，弹簧振子的位置关于平衡位置对称，位2移、速度、回复力、加速度等大反向，动能、势能大小相等。

简谐振动动力学方程推导

简谐振动动力学方程推导

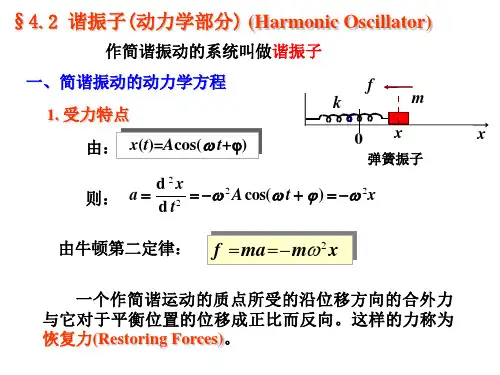
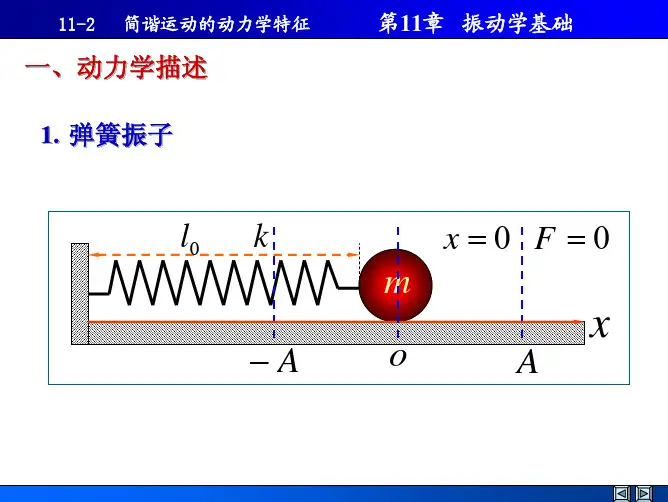
简谐振动动力学方程推导
简谐运动可以看做圆周运动的投影，所以其周期也可以用圆周运动的公式来推导。

圆周运动的；很明显v无法测量到，所以根据得到。

其中向心力F便可以用三角函数转换回复力得到即（F=-kx中负号只表示方向，所以在这省略）。

所以得到；
因为x与r之间的关系是：x=rcosα，所以上式继续化简得
到：。

然后再将v带入之前的圆周运动T中，即可得到。

将R记为匀速圆周运动的半径，即：简谐运动的振幅；
将ω记为匀速圆周运动的角速度，即：简谐运动的圆频率，
则：；
将φ记为 t=0 时匀速圆周运动的物体偏离该直径的角度（逆时针为正方向），即：简谐运动的初相位。

则，在t时刻：
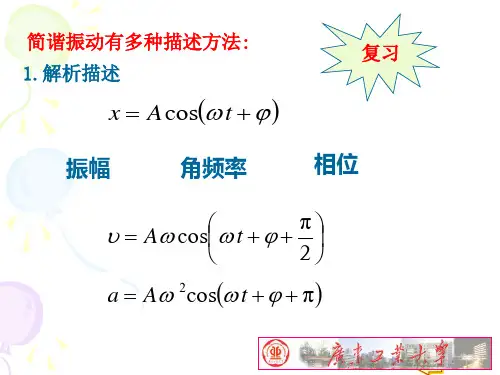
简谐运动的位移x=Rcos（ωt+φ）；
简谐运动的速度v=-ωRsin（ωt+φ）；
简谐运动的加速度a=-ω2Rcos（ωt+φ），上述三式即为简谐运动的方程。

简谐运动的表达式动力学表达式

简谐运动的表达式动力学表达式
动的依据） 2.对称性——简谐振动物体具有对平衡位置的对称
性，在关于平衡位置对称的两个位置，动能、势 能相等，位移、回复力、加速度大小相等，方向 相反,速度大小相等，方向可能相同，也可能相 反,振动过程相对平衡位置两侧的最大位移值相等.
3.周期性——简谐运动的物体经过相同时间t=nT(n) 为整数,必回复到原来的状态,经时间t=(2n+1) T2 (n为整数)，则物体所处的位置必与原来的位置 关于平衡位置对称，因此在处理实际问题中，
图2 3.简谐运动的能量
简谐运动过程中动能和势能相互转化，机械能 守恒，振动能量与 振幅 有关， 振幅 越大， 能量越大.
二、简谐运动的两种基本模型
弹簧振子（水 平）
单摆
模型示意图
条件 平衡位置
回复力
忽略弹簧质量、 无摩擦等阻力
细线不可伸长、质量 忽略、无空气等阻力、 摆角很小
弹簧处于原长处
最低点
度方向上的力充当向心力，即F向=F-mgcosθ；摆 球重力在平行于速度方向上的分力充当摆球的回复
力.当单摆做小角度摆动时，由于F回=-mgsinθ= - mg x=-kx，所以单摆的振动近似为简谐运动.
l
3.单摆的周期公式 (1)单摆振动的周期公式T=2π l ,该公式提供了
g
一种测定重力加速度g的方法. (2)l为等效摆长,表示从悬点到摆球重心的距离, 要区分摆长和摆线长，悬点实质为摆球摆动所在
2. 简谐运动的描述 （1）描述简谐运动的物理量 ①位移x：由平衡位置指向振动质点所在位置的 有向线段表示振动位移，是矢量. ②振幅A：振动物体离开平衡位置的最大距离， 是标量，表示振动的强弱. ③周期T和频率f:做简谐运动的物体完成 一次 全振动所需要的时间叫周期，而频率则等于单 位时间内完成 全振动的次数 ；它们是表示振动 快慢的物理量.二者互为倒数关系.

谐振子

谐振子

O
2) 由： A
02
2 0
和已知条件：
2
0
x0
b
x0
mg k
0.05
m
b
O' 0
x0
可得：A 0.07 m
x
3)
由
tg 0
0 0
1
和初速度为负值，可知：0 4
4) (t) Acos(t ) 0.07cos(4t 4) (m)
5) E 1 kA2 0.039 (J) 6) 做图略
x0
和速度
0，由：
x0
Acos Asin
0
联立可得：
A
x02
2 0
2
tg1( 0 ) x0
简谐运动实例：
( 1 ) 单摆
准弹性力：
l
1. 细线质量不计 约
ft mg
定 2. <5 以保证sin 由牛顿定律：
m
ft
3. 阻力忽略不计
ft
பைடு நூலகம்
mg
mat
m
l
ml
d2
dt 2
mg
d2g 0
dt2 l
一个作简谐运动的质点所受的沿位移方向的合外力 与它对于平衡位置的位移成正比而反向。这样的力称为 恢复力(Restoring Forces)。
2. 动力学方程 (以水平弹簧振子为例)
由 f ma m d2 x dt2
及 f kx 得
f
k
m
0x
x
弹簧振子
d2 x m d t 2 kx
d 2x dt2
§4.2 谐振子(动力学部分) (Harmonic Oscillator)

简谐振动方程

简谐振动方程
简谐振动的方程
一、简谐振动的动力学方程
1.弹簧振子
l0 k
m
d2x m dt2
F
kx
A o
x
A
k 2
m
d2x k
dt 2
m
x0
d2 dt
x
2
2
x
0
(1)
2 单摆
sin
(ml
2
)
d2
dt 2
M mgl
d2
dt 2
g l
0
(2)
记 2 g x
l
d2x dt 2
2x
0
(1)
O
l
T
mg
mg k
1
1
(m
2kh M
)g
一、简谐振动的动力学方程
小
d2 dt
x
2
2
x
0
结
二、简谐振动的运动学方程
x Acos(t )
t t A
t
t 0 x
o
x
x Acos(t )
旋转矢量法
初始条件确定A 初位相
例:如图m=2×10-2kg,弹簧的静止形变为l=9.8 cm. t=0 时,x0=-9.8cm,v0=0
2 描述简谐振动的特征量
(1)振幅 A
x Acos(t )
(2)周期、频率、圆频率
弹簧振子 k
m
单 摆 g
l
T 2 m
k
T 2 l
g
1 k 2 m
1 g 2 l
复 摆 mgh T 2 I 1 mgh
I
mgh
2 I
(3) 位相和初位相
x A cos(t 0 )

11-2 简谐运动的动力学特征

11-2 简谐运动的动力学特征

d2 x = ω 2 x a= 2 dt
d 2θ β = 2 = ω 2θ dt
11-2
简谐运动的动力学特征
第11章 振动学基础
二,简谐运动的能量
F = kx
x = A cos( ω t + ) v = A ω sin( ω t + )
1 2 2 E = Ek + Ep = kA ∝ A 2
d 2U 2 +ω U = 0 如:交流电压U 2 dt
ω为常数
11-2
简谐运动的动力学特征
第11章 振动学基础
2.单摆
θ <5
回复力矩
时 , sinθ
ห้องสมุดไป่ตู้
≈θ
A
M = mgl sin θ
≈ mglθ
转动 正向
θ l
FT
负号: 力矩的转向与角位移的转向相反 由转动定律: M = J β
m
o
J = ml
2
dθ mglθ = J 2 dt
2
P
11-2
dθ mglθ = J 2 dt d 2θ g = θ 2 dt l 2 dθ 2 β = 2 = ω θ dt
简谐运动的动力学特征 2
第11章 振动学基础
J = ml
2
2
g 令ω = l
与θ 成正比且反向
θ = θ m cos( ω t + )
3
x =
2
2 Ep mω
2
= 0.5 × 10 m
4
2
x = ±0.707cm
�
o
能量
xt
T
=0 t x = A cosωt v t v = Aω sin ω t

简谐振动的动力学方程

简谐振动的动力学方程


1 T
t T
Ek dt
t
1 kA2 4
E P

1 T
t T

E dt P
t

1 kA2 4
(3) 机械能
E

Ek

Ep

1 kA2 2
简谐振动系统 机械能守恒
(3) 机械能
E

Ek

Ep

1 kA2 2
弹簧振子总的机械能和振幅的平方成正比， 这一结论对其它的简谐振动系统也是正确的， 从能量的角度看振幅不仅反映振动的幅度， 还反映振动的强度
k max
2
k min
P max
2
P min
1 KA2 2
o
EE
P
K
x
E
E E
K
P
t
E 1 kA2 sin 2 ( t )
K
2
E 1 kA2 cos2 ( t )
P
2
E
1 kA2 , E
0
k max
2
k min
E
1 kA2 , E
0
P max
2
P min
Ek
O
l
m o
t 时刻细绳与竖直方向
夹角为θ
忽略空气阻力，
小球受力如图.
小球所受合外力矩为

M M M
T
G
选择逆时针方向为正
●
l
T
o mg
M mgl sin
M 0 T
M mgl sin G
M mgl sin
由转动定律 d 2
M J dt 2

简谐运动的动力学方程

简谐运动的动力学方程
在振动过程中, 物体所受到的合外力与其相对于平衡位 置的位移成正比而反向(始终指向平衡位置), 这样的力称为 线性恢复力.
简谐运动的动力学方程
由牛顿第二定律
m d 2x kx dt2
或
d2x k x 0
dt2 m
令
2 k
m
得
d2x2 x 0
dt2
—简谐运动动力学方程
微分方程的解为 x Acos(t)
(1)单摆
如图, 细线的上端固定, 另一 端悬挂一可看作质点, 质量为 m 的重物, 细线的质量和伸长可忽 略不计. 这一振动系统叫做单摆. 重物叫做摆球, 细线叫做摆线.
若把摆球从平衡位置略为拉 开后放手, 摆球就在竖直平面内 来回摆动.
解: 规定: 右方顺时针 > 0 左方逆时针 < 0
在忽略空气阻力的情况下, 合外力沿 切线方向的分力(即重力分力) 为
它拉开一个微小角度 θ后释放. 若忽
略阻力和摩擦力, 则物体将绕轴 O作微 小的自由摆动. 这样的装置叫做复摆.
简谐运动的动力学方程
简谐运动的动力学方程
解: 复摆在力矩 M的作用下的作用下的作用下的作用下,,由
定定轴律转动定M律由m定g轴l转J动定d律2由定轴转动定律由定轴转动
dt2
动力学方程为 d2 mgl
Fτ mgsin
切向运动方程为
mgsin maτ ml
d2
dt2
即
d2 g sin 0
dt2 l
为非简谐运动.
简谐运动的动力学方程
Fτ
当θ很小时 < 50 0.0873rad sin
为简谐运动 d22
dt2
0
单摆的角频率和周期分别为

振动与波动第1讲——简谐运动及其描述

振动与波动第1讲——简谐运动及其描述

m

A cos(t );
M A M0 a n t

O
x
X
初相位： ; 频率： ; 周期： T 速度： m sin( t ) A sin( t )
加速度：a an cos( t ) A 2 cos( t )
图 19
O x
解：k = m0g / Dl

0.1 9.8 N/m 12 .25 N/m 0.08
图 19
12.25 1 k/m s 7 s 1 0.25
21 2 A x v / 4 ( ) cm 5 cm 7
2 0 2 0 2 2
O x
tg v 0 /( x0 ) (21) /(4 7) 3 / 4
2
mg
0 cos(t )
2、复摆
d M mgl sin J 2 , dt 2 d mgl mgl sin 2 J dt J
2
O

l
C
mg

( 要求 5 )
可见
mgl / J , mgl / J ,
2
2 J T 2 , mgl
作业： 做习题6.3、6.4、6.10、6.18； 预习：§6.4-6.7 复习：本讲
0 cos(t )
四、旋转矢量图示法
1、旋转矢量图示法 旋转矢量 作匀速圆周运动的 质点对圆心O的矢径。 旋转矢量图示法
M A
t
O

M0
X
用旋转矢量及质点运动的相关物理量形象地 表示简谐运动的物理量的方法。
四、旋转矢量图示法

简谐运动的动力学方程

简谐运动的动力学方程
定作简谐运动。 也就是说，质点在与对平衡位 置的位移成正比而反向的合外力作用下的运动就 是简谐运动。其为简谐运动的动力学定义。
7
讨论2
得到
比较
a

d 2x dt 2

2 x
d2x dt 2

k m
x

0
简谐运动的角频率
k m
令 2 k
m
简谐运动的周期 T 2π m k
d2x dt 2
摆球的切向加速度为：
a
l
d 2
dt 2
转动
A
正向
l

FT m
o
P
9
由牛顿第二定律
ml
d 2
dt 2
mg
d 2
dt 2

g
l

0
具有
d2x k dt 2 m x 0
的形式
在角位移很小的情况下，单 摆的振动是简谐运动。
转动
A
正向
l

FT m
o
P
10
m cos(t )

2x

0
简谐运动的周期和频率仅与振动系统本身的物理 性质有关。这一周期和频率分别叫振动系统的固 有周期和固有频率。
8
2. 三个简谐振动的实例
(1) 单摆 一个质量可以忽略不 计并且不会伸缩的细线，上 端固定，下端系一可看作质 点的重物就构成一个单摆。
5 时 ,sin
Ft mg sin mg
振幅
A

2 A1 cos 2π
2
1
2
t
Amax 2 A1 Amin 0

机械振动

机械振动

例.试画出 试画出x=Acos(ωt+π/4)的x~t 图线 试画出 的
x ω a x
•
a′
•
• •
b′ T/2 5T/8
π/4
b c d o e o
•
T
T/8
•
•
t
c′ •
•d′
• e′
例题.P9 例题
一轻弹簧的右端连着一物体,弹簧的劲度系数为 一轻弹簧的右端连着一物体 弹簧的劲度系数为k=0.72N/m, 物 弹簧的劲度系数为 体的质量m 把物体从平衡位置向右拉到x 体的质量 =20g. (1)把物体从平衡位置向右拉到 = 0.05m 处 把物体从平衡位置向右拉到 停下后再释放, 求简谐运动方程; (2)求物体从初位置运动到第 停下后再释放 求简谐运动方程 求物体从初位置运动到第 一次经过A/2处时的速率 (3)如果物体在 = 0.05m处时速度不 处时的速率; 如果物体在 如果物体在x 一次经过 处时的速率 处时速度不 等于零, 而是具有向右的初速度v 求其运动方程. 等于零 而是具有向右的初速度 0= 0.30m/s, 求其运动方程 解（1）先求角频率 、振幅 、初相位 ）先求角频率ω 振幅A、初相位φ 2 k 0.72 v0 −1 2 ω= = = 6.0s A = x0 + 2 = x0 = 0.05m m 0.2 ω − v0 tgϕ = =0 ϕ = 0或π 由旋转矢量图知φ=0 由旋转矢量图知 ωx0 所以运动方程为： 所以运动方程为：
x = Acos(ωt + ϕ)
A、φ为待定系数 、 为待定系数
那么速度为: 那么速度为 式中v 式中 m=ωA 为速度振幅 加速度为: 加速度为 式中a 式中 m= ω2A 为 加速度振幅

简谐振动的运动学

简谐振动的运动学
上页 下页 返回 结束
第九章 振 动
ω v = − A ω sin( ω t + ϕ ) π = Aω cos(ωt + ϕ + ) 2 2 a = − A ω cos( ω t + ϕ )
= Aω cos(ωt + ϕ + π )
2
x = A cos(ωt + ϕ ) 2π T= 取ϕ = 0
A −A
下页 返回 结束
x = Acos(ω0t + α )
第九章 振 动
讨论
0 = A cos α
已知 t = 0, x = 0, v0 < 0 求
π α =± 2
r v
α
x
Q v0 = − Aω0 sin α < 0
o
x
∴ sin α
π > 0取 α = 2
x −t图
T
T 2
π x = A cos(ω0t + ) 2
上页
下页
返回
结束
第九章 振 动 [例题 某简谐振动规律为 x = A cos( 10 t + α ) 初始条件 例题3] 例题 求该振动的初相位. 为 t = 0, x0 = 1, v0 x = −10 3 ，求该振动的初相位 [解] 解
x = Acos(ω0t + α )
vx = − Aω0 sin(ω0t + α )
上页
下页
返回
结束
第九章 振 动
ω
t =t
ωt + ϕ
v A
x
o
x = A cos(ωt + ϕ )
以 o 为原 v 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

102简谐运动的动力学方程
1. 选择题
1，一弹簧振子，物体的质量为m ，弹簧的劲度系数为k ，该振子作振幅为A 的简谐振动。

当物体通过平衡位置且向规定的正方向运动时开始计时。

则其振动方程为： (A) )2
1/(cos π+=t m k A x ； (B) )21/cos(π-=t m k A x ；
(C) )2
1/cos(
π-=t k m A x ； (D) t m /k A x cos
=。

[ ]
2，一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2。

将它们拿到月球上去，相应的周期分别为1T '和2T '。

则有
(A) 11T T >'且22T T >'； (B) 11T T <'且22T T <'；
(C) 11T T ='且22T T ='； (D) 11T T ='且22T T >'。

[ ]
3，两个质量分别为1m 、2m 并由一轻弹簧的两端连结着的小球放在光滑的水平桌面上。

当1m 固定时，2m 的振动频率为2ν，当2m 固定时，1m 的振动频率1ν为：
（A ）2ν ； （B ）122
m m ν ； （C ）221
m m ν ； （D
）2
ν
[ ]
4，两个质量相同的物体分别挂在两个不同的弹簧下端，弹簧的伸长分别为1l ∆和2l ∆，且1l ∆=22l ∆，两弹簧振子的周期之比T 1：T 2为
（A ）2； （B ）
2； （C ）
2
1； （D ）2/1。

[ ]
5，同一弹簧振子悬挂相同的质量，分别按如图（a ）、（b ）、（c ）所示的三种方式放置，摩擦力
都忽略不计，它们的振动周期分别为a T 、
b T 、
c T ，则三者之间的关系为
（A ）a b c T T T == ； （B ）a b c T T T => ； （C ）
a b c T T T >> ； （D ）a b c T T T << 。

[ ]
6，如图所示，质量为m 的物体由劲度系数为k 1和k 2的两个轻弹簧连接在水平光滑导轨上作微小振动，则该系统的振动周期为
(A)
T =
； (B)
2T = ；
（a ）
（b ）
（c ）
(C)
2
T=；(D)
2
T=。

[ ]
7，如图所示，质量为m的物体，由劲度系数为k1和k2的两个轻弹簧连接到固定端，在水平光滑导轨上作微小振动，其振动频率为
(B)
m
k
k
2
1
2
+
π
=
ν；(B)
m
k
k
2
1
2
1+
π
=
ν；
(C)
2
1
2
1
2
1
k
mk
k
k+
π
=
ν；(D)
)
(
2
1
2
1
2
1
k
k
m
k
k
+
π
=
ν。

[ ] 8，一质量为m的物体挂在劲度系数为k的轻弹簧下面，振动角频率为ω ，若把此弹簧分割成二等份，将物体m挂在分割后的一根弹簧上，则振动角频率是
(A) 2ω ；(B) ；(C) 2
/
ω；(D) /2
ω。

[ ]
2. 判断题
1，简谐振动的周期、频率及圆频率由初始条件决定。

2，一给定劲度系数的弹簧振子作简谐振动，若弹簧所悬挂物体的质量m不同，则其振动频率也不同。

3，质点在与对平衡位置的位移成正比而反向的合外力作用下的运动就是简谐运动。

4，任何一个实际的弹簧都是有质量的，如果考虑弹簧的质量，弹簧振子的振动周期将变大。

3. 填空题
1，在两个相同的弹簧下各悬一物体，两物体的质量比
12
:
m m为4:1，则二者作简谐
振动的周期之比
12
:
T T为_______________________。

2，一弹簧振子，弹簧的劲度系数为k，重物的质量为m，则此系统的固有振动周期为______________________。

3，用40Ｎ的力拉一轻弹簧，可使其伸长20 cm。

此弹簧下应挂__________kg的物体，才能使弹簧振子作简谐振动的周期T = 0.2π s。

4，将质量为0.2 kg的物体，系于劲度系数k = 19 N/m的竖直悬挂的弹簧的下端。

假定在弹簧不变形的位置将物体由静止释放，然后物体作简谐振动，则振动频率为__________。

5，一个弹簧振子，第一次用力把弹簧压缩x后开始振动，第二次把弹簧压缩2x后开始振动，则两次振动的周期之比为。

6，摆球质量为m，摆长为l的单摆，当其作角谐振动时，从正向最大偏移位置运动到正向角位移一半处，所需的最短时间是。

7，一物块悬挂在弹簧下方作简谐振动，当这物块在平衡位置时，弹簧的长度比原长长
∆l ，这一振动系统的周期为________________。

8，有两相同的弹簧，其劲度系数均为k 。

把它们串联起来，下面挂一个质量为m 的重物，此系统作简谐振动的周期为___________________。

4. 计算题
1，一质量为0.20 kg 的质点作简谐振动，其振动方程为 10.6cos(5)2
x t =+
π (SI)
求：(1) 质点的初速度； (2) 质点在正向最大位移一半处所受的力。

2，质量为2 kg 的质点，按方程0.2sin[5]6
x t =-
π （SI ）沿着x 轴振动。

求：
(1) t = 0时，作用于质点的力的大小；
(2) 作用于质点的力的最大值和此时质点的位置。

3，由质量为M 的木块和劲度系数为k 的轻质弹簧组成在光滑水平台上运动的谐振子，如图所示。

开始时木块静止在O 点，一质量为m 的子弹以速率v 0沿水平方向射入木块并嵌在其中，然后木块（内有子弹）作简谐振动。

若以子弹射入木块并嵌在木块中时开始计时，试写出系统的振动方程。

取x 轴如图。

M。