当前位置：文档之家 › 2单自由度系统振动1

2单自由度系统振动1

  • 格式：pptx
  • 大小：4.10 MB
  • 文档页数：76

下载文档原格式

  / 76

合集下载

振动理论07(1-2)-二自由度系统

振动理论07(1-2)-二自由度系统

振动理论(7-1)第七章二自由度系统陈永强北京大学力学系二自由度自由振动●单自由度系统⏹解释共振,计算固有频率,测振仪器原理,振动隔离●为了解释更复杂的现象，必须建立更复杂的理论⏹实际工程需要更多的自由度来描述⏹多自由度系统●二自由度系统⏹最简单的多自由度系统⏹本质上是相同的模型简化建立运动微分方程求解系统的响应特性2●典型的二自由度系统⏹耦合的弹簧-质量体系⏹两个单自由度系统通过弹簧耦合起来⏹对应的扭振/电磁激荡二自由度系统二自由度自由振动3m 1m 2●自由振动●整理之后二自由度自由振动4二自由度自由振动●假定质量和作谐振动⏹具有相同的频率⏹不同的振幅和●代入振动微分方程：5方程有非零解的条件为和的系数行列式为零●上式展开后是的二次方程，即为频率方程，或称特征方程●有两个根，称为特征值，确定了系统的两个固有频率6现在从另一个角度考虑这一问题方程组在任何瞬时都成立的条件：求出和使上面方程成立7得到频率方程：令，，，有解得这就是系统的两个固有频率：第一阶固有频率(基频)和第二阶固有频率8自由振动的振幅比利用第二个方程其中, 9B 频率方程改写成圆方程的形式：二自由度自由振动O D A EC2a OA ω=2b OB ω=2abBC ω=作图法：Mohr’s circle10考虑如下对称简化情形：,二自由度自由振动k x 1kmm x 2k 311系统的固有频率二自由度自由振动k 1x 1k 2m 1m 2x 2k 3起始扰动：1,起始扰动：,起始扰动：x 1=+1,x 2=0节点12二自由度自由振动起始扰动：x1=+1,x2=0看成是两部分的和：1. ＋2.－11221211cos cos2211cos cos22x t tx t tωωωω=+=-假定振动是以下两个运动的迭加：满足微分方程和初始条件，因而是正确的解13●持续振动是第一种振动方式（振幅和频率）,迭加在第二种方式的振动上（振幅,频率)●只要不为零，和必不相等，因此合成运动肯定不是正弦运动●如果相对很小，和很接近，合成运动会有拍的现象发生，两个频率之间的差别会把两个振动的相位改变。

第1章--单自由度系统的自由振动题解

第1章--单自由度系统的自由振动题解

习 题1-1一单层房屋结构可简化为题1-1图所示的模型，房顶质量为m ，视为一刚性杆；柱子高h ，视为无质量的弹性杆，其抗弯刚度为EJ 。

求该房屋作水平方向振动时的固有频率。

解：由于两根杆都是弹性的，可以看作是两根相同的弹簧的并联。

等效弹簧系数为k 则 mg k δ=其中δ为两根杆的静形变量，由材料力学易知δ=324mgh EJ=则 k =324EJh设静平衡位置水平向右为正方向，则有 "m x kx =- 所以固有频率3n 24mhEJp =1-2 一均质等直杆，长为 l ，重量为W ，用两根长h 的相同的铅垂线悬挂成水平位置，如题1-2图所示。

试写出此杆绕通过重心的铅垂轴作微摆动的振动微分方程，并求出振动固有周期。

解：给杆一个微转角2a ＝h题1-1图题1-2图θF sin α2θαhmgθ2F cos ＝mg由动量矩定理：aha mg a mg Fa M ml I M I 822cos sin 12122-=-≈⋅-====αθαθ&&其中12cossin ≈≈θααhl ga p ha mg ml n 22222304121==⋅+θθ&& g h a l gah l p T n 3π23π2π222===1-3求题1-3图中系统的固有频率，悬臂梁端点的刚度分别是k 1和k 3，悬臂梁的质量忽略不计。

解：悬臂梁可看成刚度分别为k 1和k 3的弹簧，因此，k 1与k 2串联，设总刚度为k 1ˊ。

k 1ˊ与k 3并联，设总刚度为k 2ˊ。

k 2ˊ与k 4串联，设总刚度为k 。

即为21211k k k k k +='，212132k k kk k k ++='，4241213231421432421k k k k k k k k k k k k k k k k k k k k ++++++=)(42412132314214324212k k k k k k k k k k m k k k k k k k k k p ++++++=1-4求题1-4图所示的阶梯轴一圆盘系统扭转振动的固有频率。

结构力学课件15动力学(1)

结构力学课件15动力学(1)

（计个3算最）时便两可于个根计外据算形体来相系选似的用的具。结体构情，况如，果视周δ期、相k差、悬Δs殊t 三，参则数动中力哪性一
能相差很大。反之，两个外形看来并不相同的结构，如果其
2自021振/7/2周3 期相近，则在动荷载作用下的动力性能基本一致。2
例4、图示三根单跨梁，EI为常数，在梁中点有集中质量m， 不考虑梁的质量，试比较三者的自振频率。
EI
l
w=
k11 =
3EI l3
+k
m
m
•对于静定结构一般计算柔度系数方便。
•如果让振动体系沿振动方向发生单位位移时，所有刚节点
都不能发生转动（如横梁刚度为∞刚架)计算刚度系数方便。
两端刚结的杆的侧移刚度为：
12 l
EI
3
一端铰结的杆的侧移刚度为：
2021/7/23
3 EI l3
5
五、阻尼对自由振动的影响
忽略阻尼影响时所得结果 大能体不上能 反映实际结构的振动规律。
忽略阻尼的振动规律
考虑阻尼的振动规律
结构的自振频率是结构的固有特性，与外因无关。
简谐荷载作用下有可能出现共振。
自由振动的振幅永不衰减。
自由振动的振幅逐渐衰减。
共振时的振幅趋于无穷大。 共振时的振幅较大但为有限值。
产生阻尼的原因：结构与支承之间的外摩擦；材料之间的内摩
擦；周围介质的阻力。
阻尼力的确定：总与质点速度反向;大小与质点速度有如下关系：
①与质点速度成反比（比较常用，称为粘滞阻尼）。
②与质点速度平方成反比（如质点在流体中运动受到的阻力）。
③与质点速度无关（如摩擦力）。
粘滞阻尼力的分析比较简单，(因为R(t)=－Cy ).
机械系统动力学 第三章 机械系统运动微分方程的求解1

机械系统动力学 第三章 机械系统运动微分方程的求解1

第3章 机械系统运动微分方程的求解
• 3-1机械系统运动方程求解方法-解析法 • 3-2机械系统的运动方程求解方法-数值法 • 3-3机械系统的运动方程求解方法-半解析数
值法
3-1机械系统运动方程求解方法-解析法
3-1-1 单自由度系统的振动
1.问题的提法 工程中大量的动力学问题都可以 归结于图3-1-1 单自由度振动系 统的力学模型,其动力学问题的数 学模型表示为常微分方程的初值 问题 控制方程:
n
3-1机械系统运动方程求解方法-解析法
3-1-1 单自由度系统的振动
在初始条件为 x(0) x0, x(0) x0 欠阻尼条件下，方程的定解
x(t)
ent ( x0
cos d t
x0
x0 d
sin dt)
[1
(
X st
)2 ]2 [2 (
)]2
sin(d t
)
n
n
上中的第一项为单自由度系统自由振动响应，当t
图3-1-1 单自由度振动系 统的力学模型
mx cx kx F(t)
满足初始条件:
x(0) x0, x(0) x0
3-1机械系统运动方程求解方法-解析法
3-1-1 单自由度系统的振动
2. 单自由度振动系统简谐激励作 用下的响应
运动微分方程:
mx cx kx F0 sin t
图3-1-1 单自由度振动系 统的力学模型
3-1机械系统运动方程求解方法-解析法
3-1-1 单自由度系统的振动 2）特解
特解的求法很多，有比较系数法、旋转矢量法、拉 氏变换法等，较简单快捷的方法是旋转矢量法
设特解： x2(t) X sin(t )
代入方程 mx cx kx F0 sin t
第3章 单自由度体系1(时域)

第3章 单自由度体系1(时域)

第三章单自由度体系自由振动和强迫振动时域分析3.1力学模型•单自由度体系：SDOF（Single－Degree－of－Freedom ）System•结构的运动状态仅需要一个几何参数即可以确定•分析单自由度体系的意义：1、单自由度系统包括了结构动力分析中涉及的所有物理量及基本概念。

2、很多实际的动力问题可以直接按单自由度体系进行分析计算。

3、多自由度系统在很多情况下可以转变为单自由度系统进行分析重力的影响1、考虑重力影响时，结构体系的运动方程与无重力影响时的运动方程完全一样，此时u是由动荷载引起的动力反应。

在研究结构的动力反应时，可以完全不考虑重力的影响，建立体系的运动方程，直接求解动力荷载作用下的运动方程，即得到结构体系的动力解。

2、当需要考虑重力影响时，结构的总位移为总位移=静力解+动力解应用叠加原理将结构的动力反应和静力反应相加即得到结构的总体反应。

在结构反应问题中，应用叠加原理可将静力问题（一般是重力问题）和动力问题分开计算。

重力的影响3、注意1：由于应用了叠加原理，上述结论是用于线弹性体系。

4、注意2，在以上推导过程中，假设悬挂的弹簧―质点体系只发生竖向振动，在动荷载作用之前，重力被弹簧的弹性变形所平衡，而施加荷载后，重力始终被弹性变形所平衡。

如果重力的影响没有预先被平衡，则在施加动力荷载产生进一步变形后，可以产生二阶影响问题，例如P―Δ效应。

1.1无阻尼自由振动运动方程的通解为：121212()n n i ti ts ts tu t c e c ec ec eωω−=+=+指数函数与三角函数的关系：cos sin cos sin ixixe x i x ex i x−=+=−运动方程的解：()cos sin n n u t A t B tωω=+A ，B —待定常数，由初始条件确定。

一些重要性质：（1）自振周期只与结构的质量和结构的刚度有关，与外界的干扰因素无关。

（2）自振周期与质量的平方根成正比，质量越大，周期越大（频率越小）；自振周期与刚度的平方根成反比，刚度越大，周期越小（频率越大）；要改变结构的自振周期，只有从改变结构的质量或刚度着手。

第一章(单自由度系统的振动)

第一章(单自由度系统的振动)


单自由度系统的振动方程
c
k
m
s k
c
o
u
m
u
f (t)
mu(t) k[u(t) s ] cu(t) mg f (t)
k (u s ) cu
m
mg
f (t)
mg k s
mu(t) cu(t) k u(t) f (t)（单自由度系统振动方程的一般形式）
结论：只要以系统静平衡位置为坐标原点，那么在列写系统运动方程 时就可以不考虑系统重力的作用。
问题2
k1
k2
k3
m
k4
k1 k3
k2
√
k4
问题2
k1
k2
k3
m
k4
k1
k3
k2
╳
k4 k1
k3
k2
m
k4
问题3
无质量弹性杆
刚性杆
k
m
等效
k
m
F
k F /
第一章：单自由度系统的振动
第二讲：
无阻尼单自由度系统的自由振动
•正确理解固有频率的概念 •会求单自由度无阻尼系统的固有频率
无阻尼单自由度系统的自由振动
4
o 势能：V mg(R r)(1 cos ) 1 mg(R r) 2
2
R
m 简谐运动： max sin(nt )
B
rC
Tmax
3m 4
(
R
r
)2
(n
max
)
2
A
D
mg
Vmax
1 2
mg
(
R
r
)m2 ax
Tmax Vmax
飞行器结构动力学_第1章_2014版 [兼容模式]

飞行器结构动力学_第1章_2014版 [兼容模式]

• 分析力学基础（另加） • 2DOF系统自由振动 • 动力吸振减振 • MDOF系统振动特性(阻尼/固有频率、振型） • MDOF系统响应
– 第四章：连续系统
• 杆的振动 轴的振动 • 梁的振动 薄板振动
– 第五章：结构动力学建模
• 有限元模型建立（第6章） • 结构模态分析（第7章）
第1章 概 论
第1章 概 论
现代有限元分析——结果
第1章 概 论
实验手段
地面静力实验
第1章 概 论
地面振动实验（Ground Vibration Test，GVT）
• 确保边界条件 • 激励方式
第1章 概 论
• 传感器布置 • 信号处理
F-16 GVT悬吊
第1章 概 论
风洞实验——颤振
第1章 概 论
NASA兰利
第1章 概 论
结构动力学建模（2）
• 原则 – 保持原有系统的动力学特性（或近似） – 必须和观察到的实际模型尽可能相似
• 初步设计阶段可采用一定简化，详细设计阶段 尽可能细化
• 方法 – 1.集中参数描述的离散系统 – 2.分布参数描述 – 3.两种方法的混合
• 例子： – 导弹在空中飞行；飞机在空中飞行
• 量子场理论（quantum field theory，QFT）：具有很多自由度的量子一级
的问题 第1章 概 论
背景知识（续）
牛顿
• 牛顿三定律
– 奠定了经典力学基础 • 《自然哲学的数学原理》
– 对第2、3定律给出了合理的科学和数学描述 – 阐述了动量守恒和角动量守恒原理 • 万有引力定律 – 最先给出引力的科学、准确的表达式 • 牛顿运动定律和万有引力定律 – 对经典力学进行了最完整和最准确的描述 – 适用于日常物体和天体 • 发明了微积分 – 莱布尼茨发明了现在常用的求导和积分符号
2022-2023年注册结构工程师《结构专业基础考试一级》考前冲刺卷I(答案解析23)

2022-2023年注册结构工程师《结构专业基础考试一级》考前冲刺卷I(答案解析23)

2022-2023年注册结构工程师《结构专业基础考试一级》考前冲刺卷I（答案解析）全文为Word可编辑，若为PDF皆为盗版，请谨慎购买！第I卷一.综合考点题库(共50题)1.下列关于工作面的说法不正确的是（）。

A.工作面是指安排专业工人进行操作或者布置机械设备进行施工所需的活动空间B.最小工作面所对应安排的施工人数和机械数量是最少的C.工作面根据专业工种的计划产量定额和安全施工技术规程确定D.施工过程不同，所对应的描述工作面的计量单位不一定相同正确答案：B本题解析：工作面表明了施工对象上可能安置多少工人进行操作或布置多少机械进行施工的场所空间的大小。

最小工作面指施工队为保证安全生产和充分发挥劳动效率所必须的工作面，最小工作面所对应安排的施工人数和机械数量是最多的。

2. 单自由度体系自由振动时，实测振动5周后振幅衰减为y5＝0.04y0，则阻尼比等于（）。

A.0、05B.0、02C.0、008D.0、1025正确答案：D本题解析：知识点:阻尼比的计算；单自由度体系有阻尼自由振动时，阻尼比的计算公式为。

3.某杆件与节点板采用22个M24的螺栓连接，沿受力方向分两排按最小间距排列，螺栓承载力折减系数是（）。

A.0、75B.0、80C.0、85D.O、90正确答案：D本题解析：根据《钢结构设计规范》(GB 50017—2003)第7.2.4条规定，折减系数公式为：4.钢屋盖桁架结构中，腹杆和弦杆直接连接而不采用节点板，则腹杆的计算长度系数为（）。

A.1B.0.9C.0.8D.0.7正确答案：A本题解析：根据《钢结构设计标准》（GB 50017—2017）第7.4.1条规定，除钢管结构外，无节点板的腹杆计算长度在任意平面内均应取其等于几何长度。

因此其计算长度系数为1。

5.在评定混凝土强度时，下列哪一种方法较为理想？（）A.回弹法B.超声波法C.钻孔后装法D.钻芯法正确答案：D本题解析：钻芯法是指在被测结构构件有代表性的部位钻芯取圆柱形芯样，经必要的加工后进行抗压强度试验，由抗压强度来推定混凝土的立方体抗压强度的方法。

建筑工程之结构力学讲义两个自由度体系的自由振动(参考2)

建筑工程之结构力学讲义两个自由度体系的自由振动(参考2)


1）假设位移形状函数为抛物线
Y (x) x(l x)
2

2EIl ml5 / 60
满足边界条件且与 第一振型相近
2

120EI ml4
x y
EI m
l
10.95 EI
l2 m
2）假设均布荷载q作用下的挠度曲线作为Y(x)
Y (x) q x(l 3 2lx 2 x3 ) 24EI
整理得： (12 22 )(m1Y11Y12 m2Y21Y22 ) 0
因 1 2 ，则存在：
m1Y11Y12 m2Y21Y22 0 (15.51)
两个主振型相互正交，因与质量有关，称为第一正交关系。3
由功的互等定理：
(m112Y11)Y12 (m212Y21)Y22 (m122Y12 )Y11 (m222Y22 )Y21
D

11m1

1
2
21m1
12m2
22m2

1
2
0
令


1
2
2 (11m1 22m2 ) (11 22m1m2 12 21m1m2 ) 0
1 2

1 2
(11m1
22m2 )
1
1
1
(11m1 22m2 )2 4(11 22 12 21)m1m2

2

0l qY( 0l mY 2
x)dx (x)dx
q m
x
2l 5 120EI
q 24EI
2
31 630
l
9


9.87 l2
EI m
关于模态分析的一些问题（一）

关于模态分析的一些问题（一）

关于模态分析的⼀些问题（⼀）谐响应分析为什么可以使⽤模态叠加进⾏求解？谐响应分析是个动⼒学问题，因此⼏乎每⼀本振动⼒学的书籍都会提到如何计算，⽽在⼤学⾥本科阶段⼀般的专业对此并没有较深⼊的教学，如果没有⾃学，⽽有限元软件教学的书籍通常也不会讲，所以就出现了上⾯的问题。

下⾯将书上的内容摘于此处，并对其中部分加以解释。

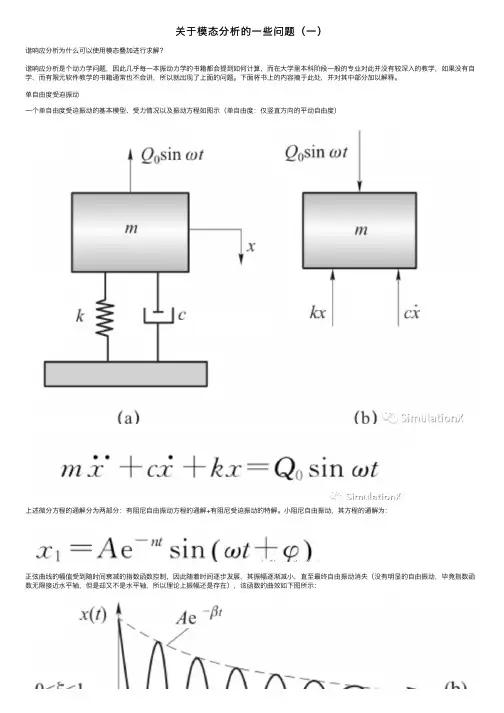
单⾃由度受迫振动⼀个单⾃由度受迫振动的基本模型、受⼒情况以及振动⽅程如图⽰（单⾃由度：仅竖直⽅向的平动⾃由度）上述微分⽅程的通解分为两部分：有阻尼⾃由振动⽅程的通解+有阻尼受迫振动的特解。

⼩阻尼⾃由振动，其⽅程的通解为：正弦曲线的幅值受到随时间衰减的指数函数控制，因此随着时间逐步发展，其振幅逐渐减⼩，直⾄最终⾃由振动消失（没有明显的⾃由振动，毕竟指数函数⽆限接近⽔平轴，但是却⼜不是⽔平轴，所以理论上振幅还是存在），该函数的曲效如下图所⽰：⼩阻尼受迫振动，其⽅程的特解为：⼩阻尼受简谐振动微分⽅程的特解还是⼀个谐函数，且该谐函数的频率与激振频率⼀致，振幅、相位取决于系统⾃⾝的固有属性和激励幅值。

让⼈⽐较好奇的是，⼤多数分析说的是激励，⽽谐响应，细品，居然说的是响应。

激励与响应具有同样的特性，都是谐函数。

实际上受到稳态激励的作⽤，其响应包括三部分组成：第⼀部分由初始条件产⽣的⾃由振动、第⼆部分由简谐激励⼒产⽣的受迫振动，第三部分是伴随受迫振动产⽣的⾃由振动。

由于系统中存在的阻尼，随时间变化，在⼀开始产⽣的⾃由振动以及伴⽣⾃由振动（伴随受迫振动产⽣的⾃由振动）逐渐消亡，仅留下稳态受迫振动部分。

因为谐响应关注的是稳态响应，开始的两类并不考虑。

⽅程耦合接触模态常听到“耦合”⼆字，那什么是耦合呢，前前后后也问过许多⼈，可真的是没有弄清楚，现在还是。

但是现在找到了合适的理解⽅法，哪怕只能意会，也可以。

耦合，想到的是“藕断丝连”，即多个对象（⼴义的对象）相互联系作⽤的⼀种关系。

观察下⾯这个例⼦就可以意会了：这是⼀个⼆⾃由度系统，其振动微分⽅程如下所⽰：将上述微分⽅程写成矩阵的形式，得到如下：上⾯的矩阵，除了质量矩阵外，刚度与阻尼矩阵都不是对⾓矩阵。

第二章1-单自由度系统无阻尼自由振动上课讲义

第二章1-单自由度系统无阻尼自由振动上课讲义


x&0 0
3 2
,2
结论1
▪ 单自由度无阻尼自由振动为简谐振动—— 位移可以表示为时间的简谐函数（正弦或 余弦）
结论2 响应满足叠加原理
▪ 系统在初始位移单独 x 0 作用下的自由振动，
此时
x&0 ， 0
x1 x0cosnt
▪ 系统在初始速度 x& 0 单独作用下的自由振动，
此时
x 0 ， 0
x2
x&0
n
sin nt
系统总响应
▪ 振动系统总的响应=上述两部分响应之和
xx1x2x0cosnt x& 0 nsinnt
▪ 叠加性是线性系统的重要特征
数字特征
▪ A ——振幅，振动物体离开静平衡位置的最
大位移
▪
▪T
n
——圆频率 ——振动周期，旋转矢量转动一周
（2 ），振动物体的位移值也就重复一次，
m& x&F
方程化简
▪ 对于无阻尼自由振动，我们有
Fkx
▪ 因此，原方程改写为：
m& x& kx0
确定微分方程的初始条件
▪ 在t=0时，初始位移为 x 0 ，初始速度为 x& 0
▪ 则方程的初始条件为：
x(0) x0 和 x&(0) x&0
完整形式
▪ 单自由度无阻尼自由振动的运动微分方程 为：
第二章1-单自由度系统无阻尼自 由振动
几种单自由度系统的示例
O θ
S
隔离体受 力分析
kx
k
x(t)
m
O
S
O θ J
2-1无阻尼自由振动
▪ 自由振动：系统在初始激励下，或外加激 励消失后的一种振动形态。

第1章 单自由度系统的振动

第1章 单自由度系统的振动1.1概述机械振动是工程中常见的物理现象。

悬挂在弹簧上的物体在外界干扰下所作的往复运动就是最简单直观的机械振动。

广泛地说，各种机器设备及其零部件和基础，都可以看成是不同程度的弹性系统。

例如桥梁在车辆通过时引起的振动，汽轮机、发电机由于转子不平衡引起的振动等。

因此，机械振动就是在一定的条件下，振动体在其平衡位置附近所作的往复性的机械运动。

实际中的振动系统是很复杂的。

为了便于分析研究和运用数学工具进行计算，需要在满足工程要求的条件下，把实际的振动系统简化为力学模型。

例如图示1.1-1就是个最简单的单自由度质量(m )—弹簧(k )系统。

如果实际系统很复杂，要求的精度较高，简化的力学模型也就复杂。

振动系统中和参数的动态特性，可以用常系数线性微分方程来描述的，称为线性振动。

但工程实际中也有很多振动系统是不能线性化的，如果勉强线性化，就会使系统的性质改变，所得的系统只能按非线性振动系统处理。

机械振动分析方法很多。

对于简单的振动系统，可以直接求解其微分方程的通解。

由于计算机进行数值计算非常方便，所以振动仿真是一种最直接的方法。

由于振动模型中尤其是多自由度振动很方便用矩阵微分方程来描述，所以MATLAB 语言在振动仿真中体现出十分优越的特性。

本章先介绍机械振动的单自由度、多自由度振动的基础，然后介绍仿真计算的各种计算公式，最后通过MATLAB 语言来实现。

1.2单自由度系统的振动1.2.1 无阻尼自由振动如图1.1-1所示的单自由度振动系统可以用如下微分方程描述：0=+kx xm (1.2.1-1) 令mkn =2ω ，方程的通解为t b t a x n n ωωcos sin += (1.2.1-2)式(1.2.1-2)表示了图示(1.1-1)中质量m 的位置随时间而变化的函数关系，反映了振动的形式与特点，称为振动函数。

式(1.2.1-2)中，a 、b 为积分常数，它决定于振动的初始条件。

1-2单自由度系统无阻尼振动(1)


选圆柱体在最低点为零势能 点，则系统势能：
圆柱体作微摆：
势能参考点的选取
势能是一个参考值，其具体值的大小和参考点选取有关。
d T U 0 在使用 dt 时，要注意，势能基准值的选 取，应使振动系统在动能最大时，势能为零。
(1)静变形法 （3）瑞利法
(2)能量法
运用能量原理，把一个分布质量系统简化为一个单自由度系统，从而把 弹簧的分布质量对系统频率的影响考虑进去，得到相对准确的固有频率值。
系统的初始条件只决定振动的振幅和初相位
结论4 系统参数对振动特性的影响
振系的质量越大，弹簧越软，则固有频率越低，周期越 长；质量越小，弹簧越硬，则固有频率越高，周期越短， 这个结论对复杂的振动系统也同样的适用。
m , k f , T m , k f , T
3 固有频率的计算
梁的等 效质量
一般来说，假定振型与实际振型之间是 有差异的。这种差异可以认为是由于系统受 到外加约束而增加了系统的刚性所致。因此 用瑞利法求出的固有频率是一偏高的近似值。
4 等效弹簧—质量系统
等效质量 等效刚度
刚度：使系统的某点在指定方向产生单位位移（或角位移）时，在该点同一 方向所要施加的力（或力矩），称为系统在该点在指定方向的刚度。 同一弹性元件，根据所要研究的振动方向不同，刚度亦不同。 左图为一端固定的等直物体，长为l，截面积为A，截面惯 性矩为J，截面极惯性矩为Jp，材料弹性模量为E，剪切 弹性模量为G。Oxy坐标如图。 分析自由端B不同方向的刚度。
解：以为广义坐标，以系统的静平 衡位置为零势能点，则：
ቤተ መጻሕፍቲ ባይዱ
若令
则得：
2.运动微分方程的求解
单自由度自由振动的微分方程：

无阻尼单自由度体系的自由振动方程

无阻尼单自由度体系的自由振动方程
无阻尼单自由度体系的自由振动方程是描述物体在无阻尼情况下自由振动的方程。

这个方程是由牛顿第二定律和胡克定律推导出来的。

我们需要了解什么是无阻尼单自由度体系。

无阻尼指的是物体在振动过程中没有受到任何阻力的影响，单自由度指的是物体只有一个自由度可以振动。

例如，一个弹簧与一个质点组成的系统就是一个无阻尼单自由度体系。

接下来，我们来推导无阻尼单自由度体系的自由振动方程。

根据牛顿第二定律，物体的加速度与作用力成正比，与物体的质量成反比。

因此，我们可以得到以下公式：
F = ma
其中，F是作用在物体上的力，m是物体的质量，a是物体的加速度。

根据胡克定律，弹簧的伸长或缩短与受力成正比。

因此，我们可以得到以下公式：
F = -kx
其中，k是弹簧的劲度系数，x是弹簧的伸长或缩短量。

将上述两个公式结合起来，我们可以得到无阻尼单自由度体系的自
由振动方程：
m(d^2x/dt^2) + kx = 0
其中，d^2x/dt^2表示物体的加速度，也就是二阶导数。

这个方程描述了物体在无阻尼情况下的自由振动。

解这个方程可以得到物体的振动周期和振幅。

振动周期是指物体完成一次完整振动所需要的时间，振幅是指物体振动时的最大位移。

无阻尼单自由度体系的自由振动方程是描述物体在无阻尼情况下自由振动的方程。

这个方程可以帮助我们了解物体的振动特性，对于研究物理学和工程学都有重要的意义。

结构抗震

单选题(共100题)(1). 抗震计算时，结构角部构件只考虑单向水平地震作用得到的地震作用效应应提高()(1分)回答:正确答案: C.30%得分: 0(2). 震级大的远震与震级小的进震对某地区产生相同的烈度，则对该地区产生的地震影响是()(1分)回答:正确答案: B.震级大的远震对柔性结构产生的震害大得分: 0(3). 下列哪一项不是多层砌体结构的抗震验算基本步骤中的内容()(1分)回答:正确答案: D.对弹性层间位移进行验算得分: 0(4). 抗震设计时，下列哪一项不在应沿柱全长加密箍筋的范围内()(1分)回答:正确答案: A.底层柱得分: 0(5). 单质点弹性体系在地震作用下的运动微分方程的特解可由下列哪一项求出？()(1分)回答:正确答案: C.杜哈密积分得分: 0(6). 土质条件对地震反应谱的影响很大，土质越松软，加速度谱曲线表现为()(1分)回答:正确答案: C.谱曲线峰值右移得分: 0(7). 下列哪一种方法不能用于框架和剪力墙协同工作的分析？()(1分)回答:正确答案: C.矩阵迭代法得分: 0(8). 对于多层砌体结构房屋，应优先采用以下哪种方案()(1分)正确答案: A.横墙承重的结构布置方案得分: 0(9). 底部框架-抗震墙房屋底部框架中水平地震作用分配()(1分)回答:正确答案: B.在弹性阶段，只考虑抗震墙抗剪得分: 0(10). 下列关于抗震横墙间距的描述，哪一项不正确()(1分)回答:正确答案: C.横墙间距过小时，楼盖刚度可能不足以传递水平地震力到相邻墙体得分: 0(11). 以下荷载：Ⅰ.水平地震作用Ⅱ.竖向地震作用Ⅲ.重力荷载Ⅳ.风荷载。

在结构抗震设计中进行荷载内力效应组合时，需要考虑的荷载包括()(1分)回答:正确答案: D.Ⅰ、Ⅱ、Ⅲ、Ⅳ得分: 0(12). 进行抗震设计时，下列哪一项关于对结构构件承载力加以调整的考虑因素是正确的()(1分)回答:正确答案: A.动力荷载下材料强度比静力荷载下高得分: 0(13). 抗震等级为一级的框架梁、柱、节点核心区、框支梁、框支柱所用混凝土强度等级不应低于()(1分)回答:正确答案: C.C30得分: 0(14). 底部剪力法中的顶部附加地震作用系数是为了考虑下列哪一项的影响？()(1分)回答:正确答案: B.高阶振型地震作用影响得分: 0(15). 多层砖房抗侧力墙体的楼层水平地震剪力分配()(1分)回答:正确答案: B.与楼盖刚度有关得分: 0(16). 下列哪一项不是高层结构抗震墙的主要震害形式()(1分)正确答案: C.墙体发生弯曲破坏得分: 0(17). 单自由度体系在下列哪一种阻尼状态下可以产生振动()(1分)回答:正确答案: C.阻尼比<1得分: 0(18). 《抗震规范》给出的设计反应谱中，当结构自振周期在0.1s-Tg之间时，谱曲线为()(1分)回答:正确答案: A.水平直线得分: 0(19). 我国建筑抗震设计规范规定隔震结构的水平向减震系数不宜低于()(1分)回答:正确答案: C.0.25得分: 0(20). 屈曲约束支撑是根据下面哪一项原理实现抗震设计的？()(1分)回答:正确答案: B.耗能减震得分: 0(21). 下列哪一项不是圈梁在砌体结构抗震中发挥的作用()(1分)回答:正确答案: D.可以提高构造柱的承载能力得分: 0(22). 按照现有的抗震设计规范设计的建筑结构，可以认为是()(1分)回答:正确答案: D.延性结构得分: 0(23). 关于地震动的卓越周期，下列哪一项是错误的()(1分)回答:正确答案: C.与地震发生的类型有关得分: 0(24). 结构进入非弹性变形状态后，下列哪一项描述正确()(1分)回答:正确答案: C.刚度矩阵改变得分: 0(25). 框架结构计算地震作用时，层剪力按各柱的刚度分配给各柱，通常需要假定()(1分)回答:正确答案: C.楼屋盖在其平面内的刚度为无穷大得分: 0(26). 以下哪一类结构无需进行多遇地震下结构允许弹性变形验算()(1分)回答:正确答案: A.砌体结构得分: 0(27). 下列哪一项关于砌体结构房屋震害规律的描述不正确()(1分)回答:正确答案: D.刚性楼盖房屋，上层破坏重、下层破坏轻得分: 0(28). 钢梁构件的滞洄模型，宜采用下述哪一种模型()(1分)回答:正确答案: C.双线性模型得分: 0(29). 通过内力组合得出的设计内力，还需进行调整，下列哪一项不是调整的目的()(1分)回答:正确答案: C.剪切破坏先于弯曲破坏得分: 0(30). 在推导地震作用下单自由度体系的运动方程时，质点上没有考虑的力是哪一项？()(1分)回答:正确答案: B.重力得分: 0(31). 抗震设计时，框架柱的截面高度和宽度均不宜小于()(1分)回答:正确答案: D.300mm得分: 0(32). 规范规定不考虑扭转影响时，用什么方法进行水平地震作用效应组合的计算？()(1分)回答:正确答案: B.平方和开方的方法（SRSS法）得分: 0(33). 计算层数较少且较为规则的框架在水平地震作用下的内力时，可采用()(1分)回答:正确答案: C.D值法得分: 0(34). 多遇地震作用下结构允许弹性变形验算的主要目的是()(1分)回答:正确答案: C.防止非结构构件破坏得分: 0(35). 9度地震区多层砌体房屋总高度和总宽度的最大比值的规定，以下哪一项正确()(1分)回答:正确答案: C.小于1.5得分: 0(36). 底层框架-抗震墙砌体房屋的过渡层，应在底部框架柱对应位置处设置构造柱。

结构动力学【习题课】(单自由度体系1)


EI l
m
4.图 所示结构周期为T 则图b 4.图a所示结构周期为Ti,则图b所示体系的周期为
T =
T1 + T + T
2 2 2
2 3
ki m
k1 k2 k3 m
(a) 5.图示体系的自振频率为 5.图示体系的自振频率为 .
(b)
EI = ∞ k
l l
m
6.图示体系的动力自由度为5. 6.图示体系的动力自由度为5. 图示体系的动力自由度为 EI=常数
第1 、2 章
小结 动力特性计算 公式法 能量守恒 幅值方程 动力反应计算 简谐荷载 周期荷载 阶跃荷载 冲击荷载 一般荷载
动荷载及其分类 自由度及其确定 运动方程的建立 惯性力法 虚功法 运动方程的求解方法 经典解法 频域解法 时域解法 数值解法 确定动力特性的试验方法 阻尼力假定及阻尼的影响
1.若使单自由度体系的阻尼增大,其结果是周期变短. 1.若使单自由度体系的阻尼增大,其结果是周期变短. 若使单自由度体系的阻尼增大 错
EA = ∞
7.体系的振幅和自振频率与初始条件有关. 7.体系的振幅和自振频率与初始条件有关. 体系的振幅和自振频率与初始条件有关
8.在图示体系中,若要使其自振频率增大,可以 8.在图示体系中,若要使其自振频率增大, 在图示体系中 A.增大 ; A.增大P; 增大 C.增大 ; C.增大m; 增大 B.增大EI; B.增大EI; 增大 D.增大 l . D.增大
ωD = ω 1−ξ 2
&& + 2ξω y + ω 2 y = P ( t ) / m & y
)
2.单自度体系运动方程为 2.单自度体系运动方程为 其中未考虑质体重力,这是因为( 其中未考虑质体重力,这是因为(

振动理论03(1)-单自由度系统自由振动

如果水在U形管中往复地振动，那么运 动质量就是 。 注意到，在这个问 题中，没有涉及弹簧。实际上，重力的 作用把水柱恢复到它的平衡位置，因此 在题目中有一个重力弹簧，按定义它的 弹性常数是单位位置变化所需要的力。
42
2014/9/28
管中其中一个臂的水位升高1厘米，另一个臂的水位就
降低1厘米，因此就给出2厘米水柱的失衡重量，产生
-任意瞬时的位置与平衡位置 之间的距离）?
10
2014/9/28
弹簧力
阻尼力
作用在质量块的力总计 sin
应用牛顿第二定律： 单自由度系统运动微分方程
mx cx kx P0 sin t
惯性力 阻尼力 弹性力 外来的谐力
单自由度扭转系统振动方程
圆盘的惯性矩为 轴的抗扭刚度为 外加扭矩 0 用于转动物体的广义牛顿定律
弹簧－质量系统
研究系统的振动问题时，常常把它简化成由若干个“ 无质量”的弹簧和“无弹性”的质量所组成的模型， 称为弹簧－质量系统(spring mass system)
角振动(angular vibration)：以角位移作为独立坐标的系 统。例如后面将要介绍的圆盘的扭振(Torsional vibration)。
用一根弹簧把一个质量m悬挂 在刚性天花板上。弹簧的刚度 由弹性系数 表示
在质量和刚性天花板之间有油 或者空气缓冲器机构
质量静止时，缓冲器不传递力 质量运动时，缓冲器的阻尼力与
速度成正比，即 c:阻尼常数或粘性阻尼常数
9
2014/9/28
假设一个交变外力作用在质 量上
计算外力造成的质量的运动 ，即求出质量运动距离 的时 间函数
振动理论(3) 第3章 单自由度系统自由振动
自由度
自由度
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 运动微分方程中，A 是机械振动系统质量块相对于振动中 心点的最大位移，称为振幅。 则是初相位，它决定了 质点运动的起始位置。 和初相位 是两个待定系数，它的大小 取决于初始条件 n , x 0 , x 0 的数值。 • 振幅和初相位都决定于初始条件，这是自由振动的共同特 性。
• 振幅 A
图2.3
单自由度系统无阻尼自由振动动力学模型
• 假设质量块的质量为 m ，它所受的重力为 W ， 弹簧刚度为 k 。弹簧未受力时的原长为 l ，挂上 质量块后，弹簧的静伸长为 j 。此时系统处于静 平衡状态，平衡位置为O-O，由静平衡条件得：
k
j
W
（2.2）
当机械振动系统受到外界某种初始干扰后，机械振 动系统的静平衡状态受到破坏，在弹性恢复力作用下， 使机械振动系统产生自由振动。若取静平衡位置为坐标 统的广义坐标，取向下为正。则当质量块离开平衡位
2 n
k m
x
2 n
x 0
齐次二阶常系数线性微分方程
C 1cos ntisin ntC 2cos ntisin
b 1cos ntb 2sin nt 式中 : b 1C 1C 2; b 2iC 1C 2
• 单自由度系统无阻尼自由振动包含两个频 率相同的简谐振动，而这两个同频率的简 谐振动，合成后仍是一个简谐振动，即：
k2 2x d 2 • 设 0 ，则上式可改写为 x 2 00 m dt 上述振动微分方程的解为 x Asin(0t )
其中固有频率 70 0 st 在初瞬时 t 0 ,物块位于未变形的梁上，其坐标
k g m
x0st 2mm , 重物初速度 v0 0, 则振幅为
F
st
mg
x
x
图2.5简支梁
• 【解】此无重弹性梁相当于一弹簧，其静挠度相当于弹簧 的静伸长，则梁的的刚度系数为
mg

列出运动微分方程为
st
重物在梁上振动时，所受的力有重力mg和弹性力 F 若取其平衡位置为坐标原点， x 轴方向铅直向下，可
d2x m 2 mg k( st x) kx dt
mm x A 02
初相角 arctan
00
v0
x arctan( ) 2 最后得系统的自由振动规律为
0
v2 0
2
2
x 2cos( 70t)mm(t以s计)
【例2-2】 试确定图2.6中各个机械振动系统的固有频率。
【解】在图2.6（a）所示的机械振动系统中，质量块m
作铅直方向位移（平动）时，引起各分弹簧的等量伸长。 重力W mg 弹簧的静伸长为j

I
M I
（2.16）
式中M——施加于转动物体上的力矩； ——转动物体对于转动轴的转动惯量； ——角加速度。
图2.7 扭转振动系统
机械振动系统圆盘的扭转的运动微分方程为
I K K 0 I
2 n
扭转自由振动的微分方程
通解
大小无关。
n
fn
•
机械振动系统质量增大和刚度减小都会使机 械系统固有频率下降；反之，要提高机械振动 系统的固有频率，应减小机械振动系统质量和 增大机械振动系统刚度。这一性质在定性研究 机械振动，特别是希望调整机械振动系统的固 有频率时是极重要的性质。
图2.4 单自由度振动系统的振幅和初相位
（3）机械振动系统的振幅和初相位
弹性元件 无质量、不耗能，储存势能的元件
阻尼元件 无质量、无弹性、线性耗能元件
质量元件 无弹性、不耗能的刚体，储存动能的元件
应用牛顿第二定律 ,图2.2(a)所示，取所有与坐标 方向一致的力、速度和加速度为正，则：
F0 sin wt Cx kx m x
如图2.2(b)所示，动静法分析知，作用在振动体上的外力 与假想加在此振动体上的惯性力组成平衡力系。这样可得： （2.1） 0
j j1 j2 j3 ji
n i1
mg j1 k1
mg j2 k2
mg j3 k3
mg mg mg mg j k k1 k2 k3 n 1 mg i1 ki
n 1 1 k i1 ki
k
1 k1k 2k 3 1 1 1 k 2k 3 k1k 2 k1k 3 k1 k3 k2
效弹簧刚度等于各分弹簧刚度之和；串联弹簧的总等效 弹簧刚度的倒数等于各分弹簧刚度倒数之和。
2.2.2扭转振动
实际上，在石油机械中常常碰到另一种需要用角 位移作广 义坐标来表达其机械振动状态的扭转振动系统和多体系统。 这些系统形式上虽然不同，但它们的运动微分方程却具有 相同的形式。 由刚体转动微分方程的表达式为：
W mg k 1
j
k 2
j
k 3
j


n
i 1
K i
j
总弹簧刚度
k
mg
j

K
i1
n
i
并联机械振动系统的固有圆频率
n
m
k m
k1 k2 k3 m
在图2.6（b）所示的机械振动系统中，若将质量块 m1和 m2 看成是由两个分质量块所组成
Cx

kx
P0 sin t
Cx
kx P 0 sin t
m x (a) m x
m x (b )
图2.2
振动体受力情况
简化过程
• 该式就是单自由度线性振动系统的运动微 分方程式的普遍式。它可以分为以下几种 不同的情况： ①单自由度系统无阻尼自由振动
m x kx 0
②单自由度系统有阻尼自由振动
在石油机械振动研究中，计算确定机械振动系统的固有频 率是很重要的。除用建立振动系统微分方程的方法外，还 有几种常用的方法，即静变形法、能量法和瑞利法。
在机械振动系统中，当质量块处于静平衡状态时，弹簧 的弹性力与质量块的重力互相平衡，即有以下关系式
k j mg k
mg
j
• 故机械振动系统的固有频率为：
m m1 m2
n1
k1 ; m1

n1

n 2 2 2

固有圆频率
n
n2
k2 m2
k1 k m 1 m m
1

k m m
2
k1m ; k
k 2m k k
k 1 k2
整个机械振动系统的固有圆频率
k k 1k2 n m m
mg
在图2.6（c）所示的机械振动系统中，质量块m的重力W 通过弹簧传至固定点。
置
时，质量块所受的作用力,重力 W 和弹性 力 k j x ，使质量块产生加速运动。
x
m x W k j x kx
即


m x kx0 （2.3）
（2.3）式即为单自由度系统无阻尼自由振动的运动微
分方程式。
k x x 0 m

通解:
int int
2

1 kA 2
2
sin
2

n
t

1 1 m n 2 A 2 cos 2 nt kA 2 sin 2 2
① 当t
2
nt E
0 时
V 0
② t
1 Tmax mn 2A2 E 2
2 n 时
（2.27）
T 0Vmax源自1 KA 22 E
（2.28）
• 由机械能守恒定律，有 Tmax Vmax
第2章 单自由度系统振动
2.1 概述
单自由度系统的振动理论是振动理论的理论基础。 例如：图2.1中(a)悬臂锤削镗杆；(b)外圆磨床的砂轮主轴；
(c)安装在地上的床身等。
图2.1 单自由度振动系统
(d)
单自由度振动系统是指用一个独立参量便可 确定系统几何位置的机械振动系统。最简单的单 自由度振动系统是一个弹簧连接一个质量的系统。 所有的单自由度机械振动系统经过简化， 用的质量都认为集中到质点上，这个质点的质量m 称为当量质量，所有的弹性都集中到弹簧中，这 个弹簧刚度k称为当量弹簧刚度。 在单自由度机械振动系统中，振动质量m、 弹簧刚度k 、阻尼系数C 是机械振动系统的三个 基本要素。有时在机械振动系统中还作用有一个 持续作用的激振力 F。
2 1 2 2
设振动系统的初始条件为： 解得：
t 0时, x x0, x x 0
1
A
x
2 0
x 02 2 tg
n
x 0 n x 0
2.2.1振动特性的讨论
(1)振动的类型
石油机械中，无阻尼自由振动是简谐振动。其振动 特性只决定于机械振动系统的弹性和质量块的惯性。
（2）系统的频率和周期
机械振动系统振动的圆频率
机械振动系统的振动频率
K n m
（2.10）
n 1 fn 2 2
K 1 m T
（2.11）
•
机械振动系统的振动周期：
T
1
fn
2
K
（2.12）
m
由此可见，机械振动系统的圆频率n和频率
fn
只与机械系统本身的物理性质（弹性和惯性）有关。 圆频率单位为弧度/秒，频率单位为赫兹。因此,当机械 振动系统的结构确定之后，机械系统的振动频率就固定 不变，而不管运动的初始条件如何，也和振幅的
1 fn 2
k 1 m 2
g
j
（2.26）
因此，知道了质量块处的弹簧静变形 确定出机械振动系统的固有频率。
。

,就可以计算
j
EJ 。其自由端有一集中质， 试求这一机械振动系统的固有频率