第章波导TE波TM波传输系统

波导工作原理波导是一种用于传送电磁波的结构，其工作原理基于电磁波在导波结构中的传播特性。

与自由空间传播相比，波导可以提供更低的传输损耗和更高的波导模式容量。

下面将介绍波导的工作原理，包括波导的结构特点和基本传输原理。

1. 波导的结构特点波导是由两个平行金属表面或传输介质构成的结构。

其横截面形状可以是矩形、圆形或其他几何形状。

波导表面可以镀上特殊的材料来提高传输效果，也可以根据需要进行加工和调整。

2. 基本传输原理波导可以支持多种模式的电磁波传输，其中最常用的是TE （横电）、TM（横磁）和TEM（横电磁混合）模式。

这些模式是根据电磁波在波导中的场分布和传输行为而定义的。

- TE模式：在TE模式中，电场垂直于波导横截面的磁场。

该模式对应于导波结构中没有电磁场在纵向传播的电磁波，称为横电场模式。

- TM模式：在TM模式中，磁场垂直于波导横截面的电场。

该模式对应于导波结构中没有电磁场在纵向传播的电磁波，称为横磁场模式。

- TEM模式：在TEM模式中，电场和磁场都存在于波导横截面上，并且在纵向传播。

该模式对应于导波结构中传输的电磁波存在横向和纵向场分量，称为横电磁混合模式。

3. 波导的传输特性波导的传输特性主要由波导的尺寸、形状和频率等因素决定。

与传统的传输线相比，波导在高频段的传输性能更好。

波导可以在多个频段中传输，其传输损耗较小，并且可以实现大功率的传输。

4. 波导的应用波导广泛应用于通信、雷达、微波加热、微波炉等领域。

例如，一些微波器件和天线系统使用波导结构传输电磁波。

波导还可用于信息传输、信号分析和测试等方面。

总之，波导的工作原理基于电磁波在导波结构中的传输特性，通过调整波导的尺寸和形状，可以实现特定模式的电磁波传输。

它在高频段的传输性能更好，并且具有较低的传输损耗和较大的传输容量。

te波和tm波模式推导TE波和TM波是电磁波在导体中传播时的两种常见模式。

TE波指的是横电波，其电场垂直于传播方向，磁场平行于传播方向；TM 波指的是横磁波，其磁场垂直于传播方向，电场平行于传播方向。

这两种模式在电磁波的传播和应用中都具有重要的意义。

TE波和TM波在传播特性上有一些不同之处。

TE波在导体中传播时，电场的分布主要集中在导体表面附近，而磁场的分布则较为均匀。

相比之下，TM波的磁场分布主要集中在导体表面附近，而电场的分布较为均匀。

这种不同的电磁场分布特性决定了它们在导体中传播的行为和响应。

TE波和TM波在应用中有着不同的用途。

TE波常用于微波技术和光纤通信等领域。

由于TE波的电场分布主要集中在导体表面附近，使得其在微波器件中具有较低的损耗和较高的传输效率。

而TM波通常用于天线设计和天线阵列等领域。

由于TM波的磁场分布主要集中在导体表面附近，使得其在天线设计中具有较高的辐射效率和较低的副瓣水平。

TE波和TM波还有一些共同的特点。

它们都是电磁波，具有电场和磁场的相互作用。

它们在导体中的传播速度都受到介质特性和频率的影响。

在低频情况下，TE波和TM波可以近似看作是标量波，其传播速度近似为光速；而在高频情况下，TE波和TM波的传播速度会受到导体的电导率和磁导率的影响，传播速度会降低。

TE波和TM波还可以相互转换。

在一些特定的结构中，TE波可以通过变换器件转化为TM波，反之亦然。

这种转换可以通过调整电场和磁场之间的耦合效应实现。

这种转换机制在微波器件设计和光纤通信系统中具有重要的应用价值，可以实现波导之间的能量传输和信号转换。

TE波和TM波是电磁波在导体中传播时的两种常见模式。

它们在传播特性、应用领域和转换机制上都有着一些不同和共同之处。

了解和掌握TE波和TM波的特性对于电磁波的传播和应用具有重要的意义。

通过合理设计和利用TE波和TM波，可以实现更高效、更稳定的电磁波传输和应用。

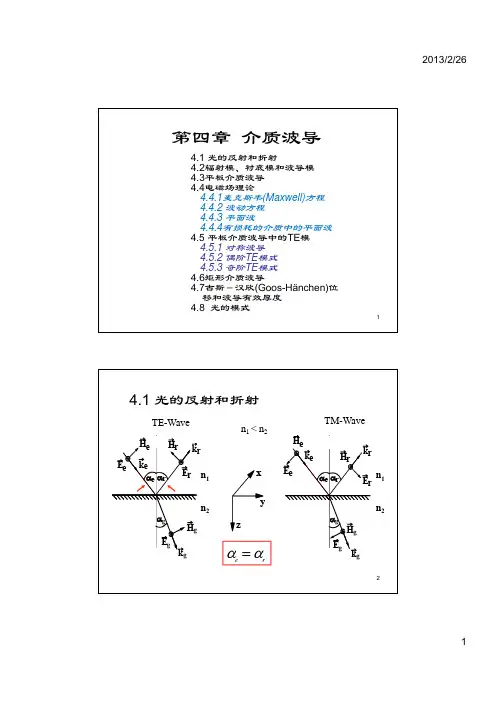
TE波与TM波第⼋章波导与谐振腔⼀导⾏电磁波的分类1 导⾏电磁波的分类为了数学上⼒求简单，把坐标的z轴选作波导的轴线⽅向，这样波导的横截⾯就是xoy平⾯，如图8—2所⽰，同时做以下假设：图8—2 任意截⾯的均匀波导(1)波导的横截⾯形状和媒质特性沿轴线z不变化，即具有轴向均匀性。

(2)⾦属波导为理想导体，即γ=∞。

波导内填充均匀、线性、各向同性的理想介质。

(3)波导内没有激励源存在，即ρ=0和J＝0。

(4)电磁波沿z轴传播，且场随时间作正弦变化。

在以上假设下，电磁场的电场分量和磁场分量均满⾜齐次的波动⽅程(8—5)(8—6)式中是波数。

既然波导轴线沿z⽅向，那么不论波的传播情况在波导内怎样复杂，其最终的效果只能是⼀个沿z⽅向前进的导⾏电磁波。

因⽽可以把波导内电场分量和磁场分量写成(8-7)(8—8)其中E(x，y)和H(x，y)是待定函数。

为波沿z⽅向的传播常数。

将(8—7)式代⼈⽅程(8—5)式，得(8-9)这⾥是横向拉普拉斯算⼦。

式中(8⼀10)同理(8—11)可以由⽅程(8—9)式和⽅程(8—11)式得到E（x，y)和H(x，y)各分量的标量波动⽅程。

也可先求解纵向场分量的波动⽅程，得到两个纵向分量Ez和Hz，然后再根据电磁场基本⽅程组求得所有横向分量。

纵向场分量Ez和Hz满⾜的标量波动⽅程为(8—12)(8—13)由上述两个⽅程求得Ez和后，即可从电磁场基本⽅程组中的两个旋度⽅程得到四个横向场分量(8-14)上式中所有场量只与坐标x和y相关。

根据以上的分析，在波导中传播的导⾏电磁波可能出现Ez或Hz分量。

因此可以依照Ez和Hz的存在情况，将在波导中传播的导⾏电磁波分为三种波型(或模式)：TEM波型、TE波型及TM波型。

横电磁波(TEM)：这种波既⽆Ez分量⼜⽆Hz分量，即Ez＝0、Hz＝0。

从(8—14)式可看出，只有当时，横向分量才不为零。

所以有或者(8—15）则⽅程（8—9)式和⽅程(8—11)式就变成(8—16)(8⼀17)这正是拉普拉斯⽅程。

第7章 导行电磁波前面我们讨论了电磁波在无界空间的传播以及电磁波对平面分界面的反射与透射现象。

在这一章中我们将讨论电磁波在有界空间的传播，即导波系统中的电磁波。

所谓导波系统是指引导电磁波沿一定方向传播的装置，被引导的电磁波称为导行波。

常见的导波系统有规则金属波导（如矩形波导、圆波导）、传输线（如平行双线、同轴线）和表面波波导（如微带线），图7.0.1给出了一些常见的导波系统。

导波系统中电磁波的传输问题属于电磁场边值问题，即在给定边界条件下解电磁波动方程，这时我们可以得到导波系统中的电磁场分布和电磁波的传播特性。

在这一章中，将用该方法讨论矩形波导、圆波导和同轴线中的电磁波传播问题以及谐振腔中的场分布及相关参数。

然而，当边界比较复杂时，用这种方法得到解析解就很困难，这时如果是双导体（或多导体）导波系统且传播的电磁波频率不太高，就可以引入分布参数，用“电路”中的电压和电流等效前面波导中的电场和磁场，这种方法称为“等效传输线”法。

这一章我们还将用该方法讨论平行双线和同轴线中波的传播特性。

7.1导行电磁波概论任意截面的均匀导波系统如图7.1.1所示。

为讨论简单又不失一般性，可作如下假设： （1）波导的横截面沿z 方向是均匀的，即导波内的电场和磁场分布只与坐标x ,y 有关，与坐标z 无关。

（2）构成波导壁的导体是理想导体，即σ=∞。

（3）波导内填充的媒质为理想介质，即0σ=，且各向同性。

（4）所讨论的区域内没有源分布，即0ρ=0=J 。

a 矩形波导b 圆柱形波导c 同轴线传输线d 双线传输线e 微带线图7.0.1 常见的几种导波系统（5）波导内的电磁场是时谐场，角频率为ω。

设波导中电磁波沿+z 方向传播，对于角频率为ω的时谐场，由假设条件（1）和（2）可将其电磁场量表示为()()()(),,,,,,,z z x y z x y e x y z x y e γγ--==E E H H (7.1.1)式中γ称为传播常数，表征导波系统中电磁场的传播特性。

第八章波导与谐振腔一导行电磁波的分类1 导行电磁波的分类为了数学上力求简单，把坐标的z轴选作波导的轴线方向，这样波导的横截面就是xoy平面，如图8—2所示，同时做以下假设：图8—2 任意截面的均匀波导(1)波导的横截面形状和媒质特性沿轴线z不变化，即具有轴向均匀性。

(2)金属波导为理想导体，即γ=∞。

波导内填充均匀、线性、各向同性的理想介质。

(3)波导内没有激励源存在，即ρ=0和J＝0。

(4)电磁波沿z轴传播，且场随时间作正弦变化。

在以上假设下，电磁场的电场分量和磁场分量均满足齐次的波动方程(8—5)(8—6)式中是波数。

既然波导轴线沿z方向，那么不论波的传播情况在波导内怎样复杂，其最终的效果只能是一个沿z方向前进的导行电磁波。

因而可以把波导内电场分量和磁场分量写成(8-7)(8—8)其中E(x，y)和H(x，y)是待定函数。

为波沿z方向的传播常数。

将(8—7)式代人方程(8—5)式，得(8-9)这里是横向拉普拉斯算子。

式中(8一10)同理(8—11)可以由方程(8—9)式和方程(8—11)式得到E（x，y)和H(x，y)各分量的标量波动方程。

也可先求解纵向场分量的波动方程，得到两个纵向分量Ez和Hz，然后再根据电磁场基本方程组求得所有横向分量。

纵向场分量Ez和Hz满足的标量波动方程为(8—12)(8—13)由上述两个方程求得Ez和后，即可从电磁场基本方程组中的两个旋度方程得到四个横向场分量(8-14)上式中所有场量只与坐标x和y相关。

根据以上的分析，在波导中传播的导行电磁波可能出现Ez或Hz分量。

因此可以依照Ez和Hz的存在情况，将在波导中传播的导行电磁波分为三种波型(或模式)：TEM波型、TE波型及TM波型。

横电磁波(TEM)：这种波既无Ez分量又无Hz分量，即Ez＝0、Hz＝0。

从(8—14)式可看出，只有当时，横向分量才不为零。

所以有或者(8—15）则方程（8—9)式和方程(8—11)式就变成(8—16)(8一17)这正是拉普拉斯方程。

第四章规则波导理论前面介绍了几种无色散的TEM波传输线，它们在结构上都属于双导体系统。

其中平行双线是用在米波波段和分米波低频端的一种传输线；同轴线是用在分米波~厘米波段的一种传输线；带状线和微带是最近20多年来发展起来的新型平面传输线，它们在微波集成电路（MIC）中做传输线或元器件之用，是属于厘米波高频端的一种传输线。

当频率再升高时，上述几种传输线出现了一系列缺点，致使它们失去了实用价值。

比如，随着频率的增高，趋肤效应显著，因而导体热损耗增加；介质损耗和辐射损耗也随之增加；横向尺寸减小，功率容量明显下降，加工工艺也愈加困难。

上述缺点促使人们寻找一种新的，适用于更高频率，具有大功率容量的传输手段，于是产生了波导管。

实际上早在第二次世界大战前的1933年就已在实验室内被证明，采用波导管是行之有效的微波功率的传输手段。

现代雷达几乎无一例外地采用波导作为其高频传输系统。

波导管的使用频带范围很宽，从915MHz（微波加热）到94GHz（F波段）都可使用波导传输线。

本章所讲的“波导”是指横截面为任意形状的空心金属管。

所谓“规则波导”是指截面形状、尺寸及内部介质分布状况沿轴向均不变化的无限长直波导。

最常用的波导，其横截面形关是矩形和圆形的。

波导具有结构简单、牢固、损耗小、功率容量大等优点，但其使用频带较窄，这一点就不如同轴线和微带线了。

导行波理论不仅用于分析各类波导传输线本身，还是下面分析谐振腔、各种微波元件等的理论基础。

§4-1 电磁场基础同前面讨论同轴线、双线传输线所用的“路”的方法不同，本章所讨论的规则波导采用的是“场”的方法，即从麦克斯韦方程出发，利用边界条件导出波导传输线中电、磁场所服从的规律，从而了解波导中的模式及其场结构（即所谓横向问题）以及这些模式沿波导轴向的基本传输特性（即所谓纵向问题）。

一、麦克斯韦方程麦克斯韦总结了一系列电磁实验定律，得出一组反映宏观电磁现象所服从的普遍规律的方程式，这就是著名的麦克斯韦方程组。

第8章导行电磁波§8.1 均匀波导的一般特性一、导波系统与导行波模式1、导波系统导波系统：在微波系统中，把电磁波能量从一处传送到另一处的装置称为导波系统。

常用的导波系统可分为以下三类：波导管：由单根封闭的柱形导体空管构成，电磁波在管内传播，简称为波导，如图4—1(a)所示的矩形波导。

传输线：由两根或两根以上平行导体构成，通常工作在其主模(TEM)或准横电磁波，故称TEM波传输线，如图4—1(b)所示的平行双线和同轴线。

表面波波导：由单根介质或敷介质层的导体构成，电磁波沿其表面传播，如图4—1(c)所示的微带线。

2、导波模式麦克斯韦方程组在特定边界条件下的一解称为电磁波的一种模式。

（1）TEM波：在电磁波的传播方向没有电场和磁场分量，称为横电磁波。

（2）TM 波：在电磁波的传播方向没有磁场分量，称为横磁波，或E 波。

（3）TE 波：在电磁波的传播方向没有电场分量，称为横电波，或M 波。

二、 导波系统的研究方法对导波系统的讨论可采用“场”和“路”的两种分析方法。

1、场分析方法(1)由麦克斯韦方程组得到导波系统内电磁场各分量间的关系。

(2)由波动方程及相应的边界条件求出导波系统内的电磁场分布。

(3)由得到的场分布可讨论导波系统内电磁波的传播特性。

2、“路”分析法在一定的条件下，以上“场”问题中的电场、磁场可用“路”问题中的电压、电流等效，这时： (1)引入分布参数，得到等效电路。

(2)利用基尔霍夫定律求出电压、电流。

(3)讨论传播特点。

三、 导波系统的场结构处理方法：由亥姆霍兹方程求出电磁场的纵向分量z z H E ,，则电磁场的横向分量y x y x H H E E ,,,可通过纵向分量求出。

1、均匀导波系统的假设(1)波导的横截面沿z 方向是均匀的，电磁波沿z 方向传播。

(2)波导壁由理想导体构成，即∞=σ。

(3)波导内填充的媒质为各向同性理想介质，即0=σ。

(4)所讨论的波导区域内没有源分布，即0,0==Jρ。