指数与指数函数测试题

高一数学测试题（指数函数）1一、选择题1．设指数函数)1,0()(≠>=a a a x f x ，则下列等式中不正确．．．的是 （ ）A ．f (x +y )=f(x )·f (y )B ．)()(y f x f y x f =-）（ C ．)()]([)(Q n x f nx f n∈=D ．)()]([·)]([)]([+∈=N n y f x f xy f n n n2．函数210)2()5(--+-=x x y（ ）A ．}2,5|{≠≠x x xB ．}2|{>x xC ．}5|{>x xD ．}552|{><<x x x 或 3．若指数函数xa y =在[－1,1]上的最大值与最小值的差是1，则底数a 等于（ ）A ．215+ B ．215- C ．215± D ．251± 4．方程)10(2||<<=a x a x 的解的个数为 （ ）A. 0个B. 1个C. 2个D. 0个或1个 5．函数||2)(x x f -=的值域是（ ）A ．]1,0(B ．)1,0(C ．),0(+∞D ．R6．函数⎩⎨⎧+≥-=-222,12)( x x f x x f x ），（，则f(-3)=（ ）A ．2B ． 3C ．4D ．87-7．已知2)(xx e e x f --=，则下列正确的是（ ）A ．奇函数，在R 上为增函数B ．偶函数，在R 上为增函数C ．奇函数，在R 上为减函数D ．偶函数，在R 上为减函数8．函数22)21(++-=x x y 得单调递增区间是 （ ）A ．]1,(--∞B ．),2[+∞C ．]2,21[D ． ]21,1[-9.已知a>0,且a ≠1,f(x)=x 2-a x.当x )1,1(-∈时，均有f(x)<21,则实数a 的取值范围是（ ） A ．⎪⎭⎫⎢⎣⎡1,21(]2,1 B.[21，1] C.(⎥⎦⎤41,0[)+∞⋃,4 D.R 10.已知偶函数f(x)，且f(x+2)=f(2-x),当-2≦x ≤0时，f(x)=2x，则f(2010)=( ) A.2010 B.4 C.41D.-4 、填空题（每小题4分，共计28分）11．当a ＞0且a ≠1时，函数f (x )=a x －2－3必过定点 12．计算：（1）48373271021.097203225.0+-⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛--π=___100；（2）⎪⎪⎭⎫ ⎝⎛-÷++-33233233421428a b b ab a ba a =32a 13．不等式x x 283312--<⎪⎭⎫⎝⎛的解集是_____14不等式2221212-++⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛a x axx 恒成立，则a 的取值范围是15．定义运算：⎩⎨⎧>≤=⊗)()(b a b b a a b a ，则函数()xx x f -⊗=22的值域为___16.已知f(x)=⎩⎨⎧>≤+-)1()1(1)2(x a x x a x,满足对任意的x 1,x 2,都有0)()(2121>--x x x f x f 成立，则实数a 的取值范围是____16.如图所示的是某池塘中的浮萍蔓延的面积(2m )与时间t (月)的关系:ty a =,有以下叙述: ① 这个指数函数的底数是2；② 第5个月时,浮萍的面积就会超过230m ； ③ 浮萍从24m 蔓延到212m 需要经过1.5个月； ④ 浮萍每个月增加的面积都相等；t/月⑤ 若浮萍蔓延到22m 、23m 、26m 所经过的时间分别为1t 、2t 、3t ，则123t t t +=. 其中正确的是 三、解答题：18．已知17a a -+=，求下列各式的值: （1）33221122a a a a----；8 （2）1122a a-+；3 （3）22(1)a a a -->.21519.已知函数)1(122>-+=a a a y x x 在区间[－1，1]上的最大值是14，求a 的值.a =3 20.（1）已知m x f x +-=132)(是奇函数，求常数m 的值； （2）画出函数|13|-=xy 的图象，并利用图象回答：k 为何值时，方程|31|x k -=无解？有一解？有两解？21．（14分）已知函数11)(+-=x x a a x f (a ＞1).（1）判断函数f (x )的奇偶性； （2）求f (x )的值域；（3）证明f (x )在(－∞，+∞)上是增函数.(4)若f(-x 2+3x)+f(m-x-x 2)>0对任意的x []1,0∈均成立，求实数m 的取值范围。

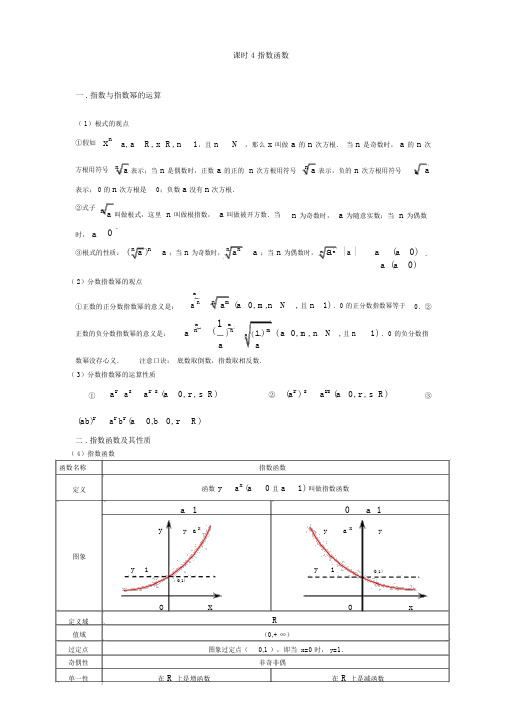
课时 4 指数函数一 . 指数与指数幂的运算（ 1）根式的观点①假如xna, a R, x R, n 1，且 nN ，那么 x 叫做 a 的 n 次方根． 当 n 是奇数时， a 的 n 次方根用符号 na 表示；当 n 是偶数时，正数 a 的正的 n 次方根用符号na 表示，负的 n 次方根用符号na表示； 0 的 n 次方根是 0；负数 a 没有 n 次方根．②式子 n a 叫做根式，这里 n 叫做根指数， a 叫做被开方数．当n 为奇数时， a 为随意实数；当 n 为偶数时， a．③根式的性质： (na )n a ；当 n 为奇数时， n a n a ；当 n 为偶数时， n a n | a |a (a 0) ．a (a 0)（ 2）分数指数幂的观点mna m (a①正数的正分数指数幂的意义是：a n 0, m,n N , 且 n 1) ．0 的正分数指数幂等于0．②m(1m1 ) m( a正数的负分数指数幂的意义是：a n)n n (0, m, n N , 且 n1) ．0 的负分数指aa数幂没存心义． 注意口诀： 底数取倒数，指数取相反数．（ 3）分数指数幂的运算性质①a r a s a r s (a 0, r , s R)② (ar) sa rs (a 0, r , s R)③(ab)ra rb r (a0,b 0, rR)二 . 指数函数及其性质（ 4）指数函数函数名称指数函数定义函数 ya x (a 0 且 a1) 叫做指数函数a 1a 1yy a xya xy图象y1y1(0,1)(0,1)OxOx定义域 R值域（0,+ ∞）过定点 图象过定点（0,1 ），即当 x=0 时， y=1．奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y ＞ 1(x ＞ 0), y=1(x=0), 0＜ y ＜ 1(x ＜ 0)y ＞ 1(x ＜ 0), y=1(x=0), 0＜ y ＜ 1(x ＞ 0)变化状况a 变化对在第一象限内， a 越大图象越高，越凑近 y 轴； 在第一象限内， a 越小图象越高，越凑近 y 轴； 图象影响在第二象限内，a 越大图象越低，越凑近x 轴．在第二象限内，a 越小图象越低，越凑近x 轴．三 .例题剖析1.设 a 、 b 知足 0<a<b<1,以下不等式中正确的选项是 ( C)A.a a <a bB.b a <b bC.a a <b aD.b b <a b 分析： A 、B 不切合底数在 (0,1) 之间的单一性 ; C 、 D 指数同样 , 底小值小 . 应选 C. 2.若 0<a<1,则函数 y=a x 与 y=(a-1)x 2 的图象可能是 (D )分析： 当 0<a<1 时 ,y=a x 为减函数 ,a-1<0, 因此 y=(a-1)x2张口向下 , 应选 D.3.设指数函数 f(x)=a x (a>0 且 a ≠ 1),则以下等式中不正确的选项是 ( D )A.f(x+y)=f(x)f(y)f (x)B.f(x-y)=f ( y)C.f(nx)= ［ f(x) ］ nD.f ［ (xy) n ］ =［ f(x) ］ n ［ f(y) ］ n (n ∈ N * )分析： 易知 A 、 B 、 C 都正确 .对于 D,f ［(xy)n］ =a (xy)n , 而［ f(x) ］ n ·［f(y) ］ n =(a x ) n ·(a y ) n =a nx+ny , 一般状况下 D 不建立 .11 34.设 a= ( 3) 3,b= ( 4)4,c= ( 3) 4,则 a 、b 、 c 的大小关系是 ( B )43 2A.c<a<b3分析： a= ( )B.c<b<aC.b<a<cD.b<c<a1 111(8133( 4)3 ( 4) 4=b, b=(4) 4)4(3) 4 =c.∴ a>b>c.3 332725.设 f(x)=4 x -2x+1,则 f -1 (0)=______1____________. 分析： 令 f -1 (0)=a, 则 f(a)=0 即有 4a -2 · 2a =0.2a · (2 a -2)=0, 而 2a >0,∴ 2a =2 得 a=1.6.函数 y=a x-3 +4(a>0 且 a ≠ 1)的反函数的图象恒过定点 ______(5,3)____________.分析： 因 y=a x 的图象恒过定点 (0,1), 向右平移 3 个单位 , 向上平移 4 个单位获得 y=a x-3 +4 的图象 , 易知恒过定点 (3,5).故其反函数过定点 (5,3).10 x 10 x.证明 f(x) 在 R 上是增函数 .7.已知函数 f(x)=x10 x10x1010x102x1,设 x 1<x 2∈ R,则f(x 1)-f(x2)=10x 1 1010x 1 10x 110x 210 x 2102 x 11 102 x 21 2(102 x 1102 x2).x 110x2 10x2 102 x1 1102 x21(102 x11)(102 x 2 1)∵ y=10 x是增函数 ,∴ 10 2x 1 10 2x 2 <0.而 10 2x 1 +1>0, 102 x 2 +1>0,故当 x <x 时 ,f(x)-f(x )<0,1212即 f(x 1)<f(x 2). 因此 f(x) 是增函数 .8.若定义运算 a b=b, ab,则函数 f(x)=3 x3-x 的值域为 ( A )a, a b,A.(0,1]B. ［ 1,+∞ )C.(0,+ ∞ )D.(- ∞ ,+∞ )分析： 当 3x ≥3-x , 即 x ≥ 0 时 ,f(x)=3-x∈(0,1 ］ ;x-x, 即 x<0 时 ,f(x)=3x∈ (0,1).3 x , x 0, 当 3<3∴ f(x)=x值域为 (0,1).3x ,0,9.函数 y=a x 与 y=-a -x (a>0,a ≠1) 的图象 ( C )A. 对于 x 轴对称B.对于 y 轴对称C.对于原点对称D.对于直线 y=-x 对称分析： 可利用函数图象的对称性来判断两图象的关系.10.当 x ∈［ -1,1］时 ,函数 f(x)=3 x-2 的值域为 _______［ -5,1 ］ ___________.3分析： f(x) 在［ -1,1 ］上单一递加 .11.设有两个命题 :(1)对于 x 的不等式 x 2+2ax+4>0对全部 x ∈ R 恒建立 ;(2) 函数 f(x)=-(5-2a) x是减函数 .若命题 (1)和 (2)中有且仅有一个是真命题 ,则实数 a 的取值范围是 _______(- ∞ ,-2)__________.分析： (1) 为真命题=(2a) 2-16<0-2<a<2. (2)为真命题 5-2a>1 a<2.若 (1) 假 (2) 真 , 则 a ∈ (- ∞ ,-2]. 若 (1) 真 (2) 假, 则 a ∈ (-2,2)∩［ 2,+ ∞］=.故 a 的取值范围为 (- ∞ ,-2).12.求函数 y=4 -x -2-x +1,x ∈［ -3,2］的最大值和最小值 .解： 设 2-x=t, 由 x ∈［ -3,2 ］得 t ∈［ 1,8 ］ , 于是 y=t 2-t+1=(t-1)2+3. 当 t= 1时 ,y3 .424有最小值 这时 x=1.当 t=8 时 ,y 有最大值57.这时 x=-3.2413.已知对于 x 的方程 2a2x-2-7a x-1 +3=0 有一个根是 2,求 a 的值和方程其他的根 . 解： ∵ 2 是方程 2a2x-2-9a x-1+4=0 的根 , 将 x=2 代入方程解得 a= 1或 a=4.2(1) 当 a= 1时 , 原方程化为 2· ( 1)2x-2-9(1) x-1 +4=0.①222x-1 2令 y=( 1) , 方程①变成 2y -9y+4=0,2解得 y 1=4,y 2= 1.∴ ( 1) x-1 =42x=-1,2( 1 ) x-1 = 1x=2.22(2) 当 a=4 时 , 原方程化为 2· 42x-2 -9 · 4x-1 +4=0. ②令 t=4 x-1 , 则方程②变成 2t 2-9t+4=0. 解得 t 1=4,t 2= 1.x-12=4x=2,∴44x-1 = 1x=- 1 .22故方程此外两根是当 a= 1时 ,x=-1;1 .2当 a=4 时 ,x=-214.函数 y= (1) 3 4xx 2的单一递加区间是 ( D )3A. ［ 1,2］B.［ 2,3］C.(-∞ ,2]D.［ 2,+∞ )分析： 由于 y=3x2-4x+3 , 又 y=3t 单一递加 ,t=x 2-4x+3 在 x ∈［ 2,+ ∞ ) 上递加 , 故所求的递加区间为［ 2,+ ∞ ).15.已知 f(x)=3 x-b (2≤ x ≤ 4,b 为常数 ) 的图象经过点 (2,1), 则 F(x)=f 2(x)-2f(x) 的值域为 ( B )A. ［ -1,+∞ )B. ［ -1,63)C.［ 0,+∞ )D.(0,63 ］分析： 由 f(2)=1, 得 32-b =1,b=2,f(x)=3 x-2.∴ F (x)= ［ f(x)-1 ］2-1=(3 x-2 -1) 2-1. 令 t=3 x-2 ,2 ≤x ≤4.2∴g(t)=(t-1) - 1,t ∈［ 1,9 ］.2.1 指数函数练习1．以下各式中建立的一项A ． ( n)71n 7 m 7B ．12 ( 3)433m3C ． 4 x 3y 3( x y) 4D ．393321111 1 52．化简 (a 3 b 2 )( 3a 2 b 3 ) ( a 6 b 6 ) 的结果3D ． 9a 2 A ． 6aB ． aC ． 9a3．设指数函数 f ( x)a x ( a 0, a1) ，则以下等式中不正确的选项是f (x) A ． f(x+y)=f(x) ·f(y)B ． f （ x y ）f ( y)C ． f (nx)[ f ( x)]n (nQ )D ． f ( xy) n [ f ( x)] n ·[f ( y)] n1 4．函数 y (x5) 0 ( x 2)2A ． { x | x 5, x 2}B ． { x | x 2}C ． { x | x 5}D ． { x | 2 x 5或 x 5}（）（）（）(n N )（ ）5．若指数函数 y a x 在 [－ 1,1]上的最大值与最小值的差是1，则底数 a 等于 （）A ．15 B ．1 5 C ．15D ．5 122 226．当 a0 时，函数 y axb 和 yb ax 的图象只可能是（）7．函数 f ( x)2 |x| 的值域是（）A ． (0,1]B ． (0,1)C ． (0, )D ． R8．函数 f ( x)2 x 1, x 0，知足 f ( x)1的 x 的取值范围1x 2 , x（）A ． ( 1,1)B ． ( 1, )C ． { x | x 0或 x2}D ． { x | x 1或 x1}9．函数 y(1) x 2x2得单一递加区间是2（）A ．[ 1,1]B ． ( , 1]C ．[2,)D ．[ 1,2]2exe x210．已知 f ( x)（）2 ，则以下正确的选项是A ．奇函数，在 R 上为增函数B ．偶函数，在 R 上为增函数C ．奇函数，在 R 上为减函数D ．偶函数，在 R 上为减函数11．已知函数 f (x)的定义域是（1， 2），则函数 f (2 x ) 的定义域是.12．当 a ＞0 且 a ≠1 时，函数 f (x)=a x －2－ 3 必过定点.三、解答题：13．求函数 y1的定义域 .x5 x 1114．若 a ＞0， b ＞ 0，且 a+b=c ，求证： (1) 当r ＞1时， a r +b r ＜ c r ； (2) 当r ＜ 1时， a r +b r ＞ c r .a x 1 15．已知函数 f ( x)(a ＞1) .a x1（ 1）判断函数 f (x) 的奇偶性；（ 2）证明 f (x)在 (－∞， +∞ )上是增函数 .xa16．函数 f(x) ＝ a (a>0 ，且 a ≠1) 在区间 [1,2] 上的最大值比最小值大2，求 a 的值．参照答案一、 DCDDD AADDA二、 11． (0,1)；12． (2，－ 2) ；三、 13． 解：要使函数存心义一定：x 1 0x 1x0 x 0x 1∴ 定义域为 ： x xR 且 x0, x 1a rrrb r此中a1,0b114． 解：ba，c rcccc.r ＞1 ，a rb ra b 1，r r r当因此+b＜ c ；时c c c crrrrr当 r ＜ 1 时， aba b1， 因此 a +b ＞c .ccc c15． 解 ：(1)是奇函数 .(2) 设x ＜x ，则 f (x 1 )ax11 ax21 。

修文县华驿私立中学2012-2013学年度第一学期单元测试卷（四）（内容：指数与指数函数 满分：150 时间：120 制卷人：朱文艺） 班级： 学号： 姓名： 得分：一、选择题：（以下每小题均有A,B,C,D 四个选项，其中只有一个选项正确，请把你的正确答案填入相应的括号中，每小题5分，共60分）1. 化简［32)5(-］43的结果为 （ ） A ．5 B ．5 C ．－5 D ．－5 2．某种细菌在培养过程中，每20分钟分裂一次（一个分裂为两个）。

经过3个小时，这种细菌由1个可繁殖成 （ ） A. 511个 B. 512个 C. 1023个 D. 1024个3.函数f(x)＝x21-的定义域是 （ ）A. (]0,∞-B. [0，＋∞）C.（－∞，0）D.（－∞，＋∞） 4. 设.)32(,)32(2.15.1-==b a 那么实数a 、b 与1的大小关系正确的是 ( )A. 1<<a bB. 1<<b aC. a b <<1D. b a <<15．在同一平面直角坐标系中，函数ax x f =)(与xa x g =)(的图像可能是 （ ）6．设dc b a ,,,都是不等于1的正数，xxxxd y c y by a y ====,,,在同一坐标系中的图像如图所示，则d c b a ,,,的大小顺序是） d c b a A <<<. c d b a B <<<. c d a b C <<<. d c a b D <<<.7. 函数xa x f )1()(2-=在R 上是减函数，则a 的取值范围是 （ ）1.>a A2.<a B 2.<a C 21.<<a D8．函数121-=x y 的值域是 （ ） )1,.(-∞A ),0()0,.(+∞-∞ B ),1.(+∞-C ),0()1,.(+∞--∞ D9．当1>a 时，函数11-+=x x a a y 是 （ ）.A 奇函数 .B 偶函数 .C 既奇又偶函数 .D 非奇非偶函数10．函数0.(12>+=-a ay x 且)1≠a 的图像必经过点 （ ）)1,0.(A )1,1.(B )0,2.(C )2,2.(D11．某厂1998年的产值为a 万元，预计产值每年以n ％递增，则该厂到2010年的产值（单位：万元）是 （ ）n a A +1(.％13) n a B +1(.％12) n a C +1(.％11) n D -1(910.％12) 12．若函数f (x )＝⎩⎪⎨⎪⎧a x，x >1(4－a2)x ＋2，x ≤1是R 上的增函数，则实数a 的取值范围为( ) A ．(1，＋∞) B ．(1,8) C ．(4,8)D ．[4,8)二、填空题(每题5分，共20分，把答案填在题中横线上)13.已知)(x f 是指数函数，且255)23(=-f ，则=)3(f . 14.设10<<a ，使不等式531222+-+->x xx x a a成立的x 的集合是 .15.函数x x y 28)13(0-+-=的定义域为 . 16.函数xx y -=22的单调递增区间为 .三、解答题(共6小题，共70分,解答应写出文字说明，证明过程或演算步骤） 17. (本题满分10分) 已知函数f (x )＝a －12x＋1，且f (x )为定义在R 上的奇函数，试求a 的值。

指数和指数函数一、选择题1．（36a 9）4（63a 9）4等于（）（C）a 4（A）a 16（B）a b 8（D）a -b 22.若a>1,b<0,且a +a =22,则a -a 的值等于（）-b b （A）6（B）±2（C）-2（D）22x 3．函数f（x）=(a -1)在R 上是减函数，则a 的取值范围是（）（A）a >1（B）a <2（C）a<2（D）1<a <4.下列函数式中，满足f(x+1)=(A)21f(x)的是( )211x -x(x+1) (B)x+ (C)2(D)224x 25.下列f(x)=(1+a )⋅a -x 是（）（A）奇函数（B）偶函数（C）非奇非偶函数（D）既奇且偶函数1a 1b116．已知a>b,ab ≠0下列不等式（1）a >b ,(2)2>2,(3)<,(4)a 3>b 3,(5)()<()33a b22a b 11中恒成立的有（）（A）1个（B）2个（C）3个（D）4个2x -17．函数y=x 是（）2+1（A）奇函数（B）偶函数（C）既奇又偶函数（D）非奇非偶函数8．函数y=1的值域是（）x 2-1（A）（-∞,1）（B）（-∞,0）⋃（0，+∞）（C）（-1，+∞）（D）（-∞，-1）⋃（0，+∞）+9．下列函数中，值域为R 的是（）（A）y=512-x（B）y=(1x 11-xx)（C）y=()-1（D）y=1-223e x -e -x10.函数y=的反函数是（）2（A）奇函数且在R 上是减函数（B）偶函数且在R 上是减函数++（C）奇函数且在R 上是增函数（D）偶函数且在R 上是增函数11．下列关系中正确的是（）++111111（A）（）3<（）3<（）3（B）（）3<（）3<（）3252225111111（C）（）3<（）3<（）3（D）（）3<（）3<（）352252221222122112212．若函数y=3+2的反函数的图像经过P 点，则P 点坐标是（）（A）（2，5）（B）（1，3）（C）（5，2）（D）（3，1）x -113．函数f(x)=3+5,则f (x)的定义域是（）（A）（０，＋∞）（B）（５，＋∞）（C）（６，＋∞）（D）（－∞，＋∞）x 14.若方程a -x-a=0有两个根，则a 的取值范围是（）（A）（1，+∞）（B）（0，1）（C）（0，+∞）（D）φ15．已知函数f(x)=a +k,它的图像经过点（1，7），又知其反函数的图像经过点（4，0），则函数f(x)的表达式是（）x x x x (A)f(x)=2+5 (B)f(x)=5+3 (C)f(x)=3+4 (D)f(x)=4+316.已知三个实数a,b=a ,c=a a x x-1a a ,其中0.9<a<1,则这三个数之间的大小关系是（）（A）a<c<b （B）a<b<c （C）b<a<c （D）c<a<bx 17．已知0<a<1,b<-1,则函数y=a +b 的图像必定不经过（）(A)第一象限 (B)第二象限(C)第三象限 (D)第四象限二、填空题1．若a <ax 322,则a 的取值范围是。

《指数与指数函数》测试题一、选择题（每小题５分，共计６０分）1 ）A ．3 B.3- C.3± D.812.30a >）的值是（ ）A ．1B ．aC ．15a D 1710a3．对于0,,a r s Q >∈以下运算正确的是（ ）A ．r s rs a a a ⋅=B ．()r s r s a a +=C ．()r r raa b b -= D ．()r s r s a b ab +⋅= 4.在某种细菌培养过程中，每30分钟分裂一次（一个分裂为两个），经过4个小时，这种细菌由一个可繁殖成（ ）A.8B.16C.256D.325．指数函数x y a =与x y b =的图象如图，则（ ）A ．0,0a b <>B ．01,01a b <<<<C ．1,01a b ><<D ．01,1a b <<>6.已知0.20.40.30.3,0.3, 1.1a b c ===，则a b c 、、的大小关系是（ ）Ａ.a b c >> Ｂ. b a c >> Ｃ. c b a >> Ｄ. c a b >>7.若x 2＝7，y 2＝6，则y x －4等于（ ） A ．4936 B ．67 C ．1214 D ．3649 8.函数2()1(0,1)x f x a a a -=+>≠必定过点（ ）Ａ．(0,1) Ｂ．(1,1) Ｃ．(2,0) Ｄ．(2,2)9.已知01,1a b <<<-，则函数xy a b =+的图像不经过（ ）Ａ．第一象限 Ｂ．第二象限 Ｃ．第三象限 Ｄ．第四象限10. 函数x y a =与y ax a =-的图象大致是下图中的（ ）11.当x ∈［－2，2)时，31x y -=-的值域是（ ）A ．［－98，8］B ．（－98，8］C ．(91，9)D ．［91，9］ 12．下列说法中，正确的是（ ）①任取x ∈R 都有3x ＞2x ；② y =x -是增函数；③ y =2|x |的最小值为1 ；④在同一坐标系中，y =2x 与2x y -=的图象对称于y 轴.A ．①②B ．③④C ．①③D ．②④二、填空题（每小题４分，共计１６分）13.求值：3481()16-= ；= . 14．方程11216x -=的解是 .15．函数()f x =_____________.16．函数x a y =在]1,0[上的最大值与最小值的和为3，则=a ．三、解答题17.（１２分）（1）计算：210319)41()2(4)21(----+-⋅- ⑵化简：215658)·(b a18. （１２分）已知函数()(0,1)x f x a a a =>≠的图象过(3,8)-，求(0),(1),(2)f f f -的值.19. （１２分）解关于x 的不等式3223x x a a -+->.20. （１２分）指数函数()xb y a =的图象如图所示：⑴在已知图象的基础上画出函数()xa yb =的图象；⑵求函数2y ax bx =+的顶点的横坐标的取值范围．21. （１２分）画出函数1()2x y =的图象，并根据图象写出其单调区间及值域.22. （１４分）某电脑公司生产Ａ型电脑，2019年这种电脑每台平均生产成本为5000元，并以纯利润0020确定出厂价.从2019年开始，公司通过更新设备和加强管理，使成本逐年降低，到2019年，尽管Ａ型电脑出厂价仅是2019年出厂价的0080，但却实现了0050的纯利润的高效益.⑴求2019年每台型电脑的生产成本；⑵以２００６年的生产成本为基数，求２００６～２０１０年生产成本平均每年降低的百分数（精确到0.01 2.449==）。

指数问题测试题及答案一、选择题1. 下列哪个表达式表示2的3次方？A. 2^3B. 2×3C. 3^2D. 2+3答案：A2. 计算2的5次方的结果是多少？A. 32B. 25C. 16D. 10答案：A3. 如果3的x次方等于27，那么x的值是多少？A. 3B. 4C. 6D. 9答案：A二、填空题4. 指数法则中，任何数的0次方等于______。

答案：15. 如果a^m = a^n，那么m等于______。

答案：n6. 指数运算中，底数相同，指数相加的法则是a^(m+n) = ______。

答案：a^m × a^n三、简答题7. 解释什么是指数函数，并给出一个例子。

答案：指数函数是一种数学函数，其中一个变量的幂等于另一个变量。

例如，y = 2^x，这是一个指数函数，其中2是底数，x是指数。

8. 描述如何计算5的4次方，并给出结果。

答案：5的4次方是将5自身乘以4次，即5 × 5 × 5 × 5 = 625。

四、计算题9. 计算下列表达式的值：(a) 4^3(b) (2^2)^3答案：(a) 4^3 = 4 × 4 × 4 = 64(b) (2^2)^3 = 4^3 = 4 × 4 × 4 = 6410. 如果8^x = 2^12，求x的值。

答案：由于8 = 2^3，我们可以将8^x写成(2^3)^x = 2^(3x)。

因此，2^(3x) = 2^12，所以3x = 12，解得x = 4。

五、证明题11. 证明对于任何正数a和b，a^b × b^a总是大于或等于a^a × b^b。

答案：由于a和b都是正数，我们可以应用AM-GM不等式（算术平均值-几何平均值不等式），即对于任意的正数x和y，有(x + y)/2 ≥ √(xy)。

将x设为a^b，y设为b^a，我们得到：(a^b + b^a)/2 ≥ √(a^b × b^a)两边同时平方，得到：(a^b + b^a)^2/4 ≥ a^b × b^a展开左边，得到：a^(2b) + 2a^b × b^a + b^(2a) ≥ 4a^b × b^a简化得到：a^(2b) - 2a^b × b^a+ b^(2a) ≥ 0这可以重写为：(a^b - b^a)^2 ≥ 0由于平方总是非负的，所以上述不等式成立。

指数与指数函数练习题一、选择题1. 指数函数\( y = a^x \)中，当\( a > 1 \)时，函数的图像是：A. 在第一象限单调递增B. 在第二象限单调递增C. 在第三象限单调递增D. 在第四象限单调递增2. 已知\( 2^x = 4 \)，则\( x \)的值为：A. 1B. 2C. 3D. 43. 对于\( y = 3^x \)，当\( x \)增加1时，\( y \)增加的倍数是：A. 1B. 2C. 3D. 44. 函数\( y = a^x \)的图像关于y轴对称的条件是：A. \( a > 1 \)B. \( a < 1 \)C. \( a = 1 \)D. \( a = -1 \)5. 如果\( a \)是正数，\( b \)是负数，那么\( a^b \)的值是：A. 正数B. 负数C. 零D. 无法确定二、填空题6. 根据指数函数的性质，\( 2^3 \)等于______。

7. 如果\( 5^x = 125 \)，那么\( x \)等于______。

8. 函数\( y = 2^{-x} \)的图像在第一象限的斜率是______。

9. 指数函数\( y = a^x \)的图像在\( x = 0 \)处的值为______。

10. 函数\( y = (1/2)^x \)的图像在\( y = 1 \)时，\( x \)的值为______。

三、简答题11. 解释指数函数\( y = a^x \)在\( x \)轴上的截距是什么，并说明为什么。

12. 描述指数函数\( y = a^x \)在\( a \)的值大于1时的增长速度。

13. 说明为什么指数函数\( y = a^x \)的图像在\( a \)小于1但大于0时，随着\( x \)的增加而递减。

14. 给定一个指数函数\( y = 2^x \)，如果\( x \)增加1，\( y \)的值会如何变化？15. 讨论指数函数在\( a \)的值小于0时的性质，并给出一个具体的例子。

指数函数测试卷姓名： 得分：1．化简［32)5(-］4的结果为（ ）A ．5B ．5C ．－5D ．－5 2．化简46394369)()(a a ⋅的结果为（ ）A ．a16B ．a8C ．a4D ．a 23．设函数的取值范围是则若0021,1)(,.0,,0,12)(x x f x x x x f x >⎪⎩⎪⎨⎧>≤-=-（ ）A ．(－1，1)B ．(－1，＋∞)C ．),0()2,(+∞⋃--∞D ．),1()1,(+∞⋃--∞4．设5.1344.029.01)21(,8,4-===y y y ，则（ ）A ．y 3＞y 1＞y 2B ．y 2＞y 1＞y 3C ．y 1＞y 2＞y 3D ．y 1＞y 3＞y 25．当x ∈［－2，2)时，y =3－x－1的值域是（ ）A ．［－98，8］ B ．［－98，8］ C ．(91，9) D ．［91，9］ 6．在下列图象中，二次函数y =ax 2＋bx ＋c 与函数y =(ab )x 的图象可能是 （ ）7．已知函数f (x )的定义域是(0，1)，那么f (2x)的定义域是（ ）A ．(0，1)B ．(21，1) C ．(－∞，0) D ．(0，＋∞) 8．若122-=xa ，则xx x x aa a a --++33等于（ ）A ．22－1B ．2－22C ．22＋1D ． 2＋19．设f (x )满足f (x )＝f (4－x )，且当x ＞2 时f (x )是增函数，则a ＝f (1.10.9)，b = f (0.91.1)，c ＝)4(log 21f 的大小关系是 （ ）A ．a ＞b ＞cB ．b ＞a ＞cC ．a ＞c ＞bD ．c ＞b ＞a10. 函数121x y =-的值域是（ ）A 、(),1-∞B 、()(),00,-∞+∞C 、()1,-+∞D 、()(,1)0,-∞-+∞11. 一批设备价值a 万元，由于使用磨损，每年比上一年价值降低%b ，则n 年后这批设备的价值为（ ）A 、(1%)na b -B 、(1%)a nb -C 、[1(%)]n a b -D 、(1%)n a b - 12. 下列说法中，正确的是 （ ）①任取x ∈R 都有3x ＞2x②当a ＞1时，任取x ∈R 都有a x ＞a －x③y =(3)－x是增函数④y =2|x |的最小值为1⑤在同一坐标系中，y =2x 与y =2－x的图象对称于y 轴 A ．①②④ B ．④⑤ C ．②③④ D ．①⑤ 二、填空题（每小题4分，计4×4=16分） 13. 已知215-=a ，函数()xf x a =，若实数,m n 满足()()f m f n >，则,m n 的大小关系为_________.14. 若关于x 的方程4x +a ·2x+4=0有实数解，则实数a 的取值范围是___________.15. 若函数()()1,0≠>-=a a b a x f x 的图象不经过第二象限，则b a ,满足的条件是 16. 若函数12)(22-=-+aax x x f 的定义域为R ，则a 的取值范围为__________.三、解答题（共计74分） 17. 已知函数332+-=x x a y 在[0，2]上有最小值8，求正数a 的值．18. 若函数4323xxy =-⋅+的值域为[]1,7，试确定x 的取值范围。

指数函数对数函数幂函数单元测试题层层飞跃，挑战巅峰——指数函数、对数函数、幂函数测试题一、选择题1.设指数函数C1：y=ax，C2：y=bx，C3：y=cx的图象如图，则（）A。

0<c<1<b<aB。

0<a<1<b<cC。

c<b<aD。

0<c<1<a<b2.函数y=a（a>0，a≠1）过定点，则这个定点是（）A。

（，1）B。

（1，2）C。

（-1，0.5）D。

（1，1）3.若函数y=f（x）的图象与y=2的图象关于y轴对称，则f（3）=（）A。

8B。

4C。

-4D。

-84.若指数函数y=ax经过点（-1，3），则a等于（）A。

3B。

2C。

1/3D。

1/25.函数y=f（x）的图象与y=2的图象关于直线x=1对称，则f（x）为（）A。

y=2x-1B。

y=2x+1C。

y=2x-2D。

y=2^(2-x)6.对于任意x1，x2∈R，恒有f（x1）·f（x2）=f（x1+x2）成立，且f（1）=2，则f（6）=（）A。

22B。

4C。

2D。

87.若函数f（x）=loga x（0<a<1）在区间[a，2a]上的最大值是最小值的3倍，则a=A。

1/4B。

1/2C。

2/2D。

2/48.在同一坐标系中，函数y=2-x与y=log2 x的图象是（）A。

y=log2(2-x)B。

y=log2(2+x)C。

y=log2(2-x)+1D。

y=log2(2+x)-19.设函数f(x)={2-x-1 (x≤2)。

x(x>2)}，若f（x）>1，则x 的取值范围是（）A。

（-1，1）B。

（-∞，-2）∪（2，+∞）C。

（-1，+∞）D。

（-∞，-1）∪（1，+∞）10.已知0<m<n<1，则a=logm(m+1)与b=logn(n+1)的大小关系是（）A。

a>bB。

a=bC。

a<bD。

桃江四中高一数学?指数与指数函数?测试题时间是：60分钟 满分是：100分一、选择题(每一小题5分，一共30分),1n N n *∈>，根据n次方根的意义，以下各式：①;n a =a ；③na =； ④na ，其中正确的有 〔 〕A.①②③④B.①③④C.①②③D.①②④ 2.1132102,1032a b -==，那么32410a b += 〔 〕3.设01a <<，那么函数x y a =的图像是 〔 〕A B C D4.,0)a b >的结果是 〔 〕 A.b a B.ab C.a bD.2a b 5.()22,()3,x x f x f a -=+=若那么(2)f a = 〔 〕 A.5 B.7 C0.90.44 1.512314,8,()2y y y -===，那么123,,y y y 的大小关系是 〔 〕 A.312y y y >> B.213y y y >> C.123y y y >> D.132y y y >>二、填空题(每一小题5分，一共30分)y =的定义域是8.函数3()1x f x a +=+的图像一定经过的定点的坐标为xxxx12x y =的值域是10.()x a f x a ==，假设实数,m n 满足()()f m f n >，那么,m n 的大小关系是 11.函数(23)y f x =-的图像可以由(2)y f x =经过怎样的平移而来？答： ()(0,1)x f x a a a =>≠在[]2,2-上的函数值总小于2，那么实数a 的取值范围是三、解答题(13分+13分+14分=40分)1,0()1,03x x x f x x ⎧<⎪⎪=⎨⎛⎫⎪≥ ⎪⎪⎝⎭⎩，求不等式11()33f x -≤≤的解集。

14.当[]0,2x ∈时，求函数1()425x x f x +=-+的值域.15.11()221x f x x ⎛⎫=+ ⎪-⎝⎭〔1〕判断()f x 的奇偶性并证明；〔2〕求证：()0f x >励志赠言经典语录精选句；挥动**，放飞梦想。