沪科版18.1勾股定理练习题

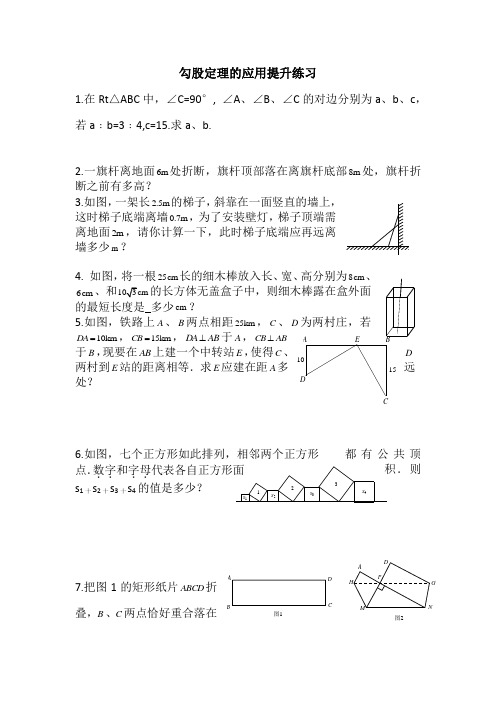
321S 4S 3S 2S 1图2图1NH P MGDADCBA勾股定理的应用提升练习1.在Rt △ABC 中，∠C=90°, ∠A 、∠B 、∠C 的对边分别为a 、b 、c ，若a ﹕b=3﹕4,c=15.求a 、b.2.一旗杆离地面6m 处折断，旗杆顶部落在离旗杆底部8m 处，旗杆折断之前有多高？3.如图，一架长2.5m 的梯子，斜靠在一面竖直的墙上，这时梯子底端离墙0.7m ，为了安装壁灯，梯子顶端需离地面2m ，请你计算一下，此时梯子底端应再远离墙多少m ？4. 如图，将一根25cm 长的细木棒放入长、宽、高分别为8cm 、 6cm、和的长方体无盖盒子中，则细木棒露在盒外面的最短长度是 多少cm ？5.如图，铁路上A 、B 两点相距25km ，C 、D 为两村庄，若10km DA =，15km CB =，DA AB ⊥于A ，CB AB ⊥于B ，现要在AB 上建一个中转站E ，使得C 、D两村到E 站的距离相等．求E 应建在距A 多远处？6.如图，七个正方形如此排列，相邻两个正方形都有公共顶点．数字．．和字母．．代表各自正方形面积．则s 1十s 2十s 3十s 4的值是多少？7.把图1的矩形纸片ABCD 折叠，B 、C两点恰好重合落在1510E DC B AA CPOBxy AD 边上的点P 处(如图2)，已知90MPN ∠=°，5PM =，12PN =，求矩形纸片ABCD 的面积．8. 如图，在平面直角坐标系中，Rt △OAB 的顶点A 在x 轴的正半轴上．顶点B 的坐标为（3，3），点C 的坐标为（12，0），点P 为斜边OB 上的一个动点，求三角形P C A 周长的最小值.9.细心观察图，认真分析各式，然后解答问题：2(1)12+=112S = 2(2)13+= 222S =2(3)14+=332S =① 用含有n （n 是正整数）的等式表示上述变化规律；② 推算出10OA 的长；③ 求出222212310S S S S ++++的值．10.如图，AD 是ABC △的中线，45ADC ∠=︒．把ADC △沿直线AD 折过来，点C 落在点C'的位置上，如果4BC =，求B C'的长．11.如图1，分别以直角三角形ABC 三边为边向外作三个正方形，其面积分别用1S 、2S 、3S 表示，则不难证明123S S S =+．⑴ 如图2，分别以直角三角形ABC 三边为直径向外作三个半圆，其面积分别用1S 、2S 、3S 表示，那么1S 、2S 、3S 之间有什么关系？（不必证明）⑵ 如图3，分别以直角三角形ABC 三边为边向外作三个正三角形，其面积分别用1S 、2S 、3S 表示，请你确定1S 、2S 、3S 之间的关系并加以证明．⑶ 四边形ABCD 的对角线互相垂直，现以四边形的边长为边长向外作四个正方形，面积分别为1S 、2S 、3S 、4S ．则1S 、C'D CBA2S 、3S 和4S 之间的关系是 ．ABC S 1S 3S 2图3ABC S 1S 3S 2图2图1S 2S 3S 1CBA S 4S 3S 2S 1DB CA。

沪科版八年级下册数学第18章勾股定理含答案一、单选题(共15题，共计45分)1、下列几组数中，是勾股数的是（）A.1，，B.15，8，17C.13，14，15D. ，，12、如图，在□ABCD中，AE⊥BC于E，AE＝EB＝EC＝a，且a是一元二次方程x2+2x-3=0的根，则□ABCD的周长为（）A. B. C. D. 或3、若一个直角三角形的一条直角边长是5cm，另一条直角边比斜边短1cm，则斜边长为（）cm．A.10B.11C.12D.134、如图，在Rt△ABC中，∠A＝90°，AB＝6，AC＝8，点D为边BC的中点，点M为边AB上的一动点，点N为边AC上的一动点，且∠MDN＝90°，则sin∠DMN 为（）A. B. C. D.5、直角三角形两直角边的长分别为3和4，则此直角三角形斜边上的中线长为（）A.1.5B.2C.2.5D.56、如图，在的正方形网格图中，小正方形的边长为1，的顶点均在格点上，则下列关于的说法错误的是（）A.是直角三角形B.tamC.面积为D. 边上的高为7、正方形网格中，△ABC如图放置，则sin∠BAC=（）A. B. C. D.8、如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的B′处，点A对应点为A′，且B′C=3，则AM的长是（）A.1.5B.2C.2.25D.2.59、如图，四边形内接于，为直径，，过点作于点，连接交于点．若，，则的长为（）A.8B.10C.12D.1610、矩形ABCD中，已知AB＝5，AD＝12，则AC长为（）A.9B.13C.17D.2011、在矩形ABCD中，AB=3，AD=5，以点A为圆心，4为半径作圆，点C与⊙A 的位置关系（）A.点C在⊙A内B.点C在⊙A上C.点C在⊙A外D.无法确定12、如图，在△ABC中，AB=AC=5，BC=8，D是线段BC上的动点（不含端点B、C）．若线段AD长为正整数，则点D的个数共有（）A.5个B.4个C.3个D.2个13、如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅少走了（）步路（假设2步为1米），却踩伤了花草．A.1B.2C.3D.414、已知，如图，长方形ABCD中，AB=5cm，AD=25cm，将此长方形折叠，使点D与点B重合，折痕为EF，则△ABE的面积为（）A.35 cm2B.30 cm2C.60 cm2D.75 cm215、如图，正方形ABCD中，AB=1，则AC的长是（）A.1B.C.D.2二、填空题(共10题，共计30分)16、如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3BE，P是AC上一动点，则PB+PE的最小值是________．17、如图，长方体的长为15 cm，宽为10 cm，高为20 cm，点B距离C点 5 cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是________cm．18、如图，菱形纸片ABCD，AB＝4，∠B＝60°，将该菱形纸片折叠，使点B恰好落在CD边的中点B′处，折痕与边BC、BA分别交于点M、N.则BM的长为________.19、矩形ABCD内一点P到顶点A、B、C的长分别是1、2、3，则PD＝________．20、如图，在中，，点P在斜边上，以为直角边作等腰直角三角形，，则三者之间的数量关系是________．21、如图，菱形ABCD的对角线AC、BD相交于点O，且AC=8，BD=6，过点O作OH丄AB，垂足为H，则点O到边AB的距离OH＝________.22、在平面直角坐标系中，点A、B的坐标分别为（ 2，0 ），（4，0），点C 的坐标为（m，m）（m为非负数），则CA+CB的最小值是________23、矩形两条对角线的夹角为60°，对角线长为14，则该矩形较长的边长为________.24、如图，正方形ABCD的边长是2，点E是CD边的中点，点F是边BC上不与点B，C重合的一个动点，把∠C沿直线EF折叠，使点C落在点C′处.当△ADC′为等腰三角形时，FC的长为________.25、如图，一架长为4m的梯子，一端放在离墙脚3m处，另一端靠墙，则梯子顶端离墙脚________．三、解答题(共5题，共计25分)26、如图，已知在△ABC中，CD⊥AB于D，AC＝20，BC＝15，DB＝9.求AB的长.27、如图：有一个圆柱，底面圆的直径EF= ，高FC=12cm，P为FC的中点，求蚂蚁从E点爬到P点的最短距离是多少？（画出平面图形）28、如图，在Rt△ABC中，∠BCA＝90°，AC＝12，AB＝13，点D是Rt△ABC外一点，连接DC，DB，且CD＝4，BD＝3.求：四边形ABDC的面积.29、如图，已知在△ABC中，CD⊥AB于D，AC=20，BC=15，DB=9．（1）求DC的长．（2）求AB的长．30、如图，∠MON=∠PMO，OP=x-3，OM=4，ON=3，MN=5，MP=11-x．求证：四边形OPMN是平行四边形。

专题18.1 勾股定理及其逆定理【九大题型】【沪科版】【题型1 勾股定理的运用】 (1)【题型2 直角三角形中的分类讨论思想】 (2)【题型3 勾股定理解勾股树问题】 (3)【题型4 勾股定理解动点问题】 (4)【题型5 勾股定理的验证】 (5)【题型6 直角三角形的判定】 (7)【题型7 勾股数问题】 (8)【题型8 格点图中求角的度数】 (9)【题型9 勾股定理及其逆定理的运用】 (10)【题型1 勾股定理的运用】【例1】（2022•和平区三模）如图，在△ABC中，∠C＝90°，AD平分∠CAB，CD＝1.5，BD＝2.5，则AC的长为（）A．5B．4C．3D．2【变式1-1】（2022春•上杭县期中）如图在Rt△ABC中，∠B＝90°，AB＝8，AC＝10，AC的垂直平分线DE分别交AB、AC于D、E两点，则BD的长为（）A ．32B ．74C ．2D ．52【变式1-2】（2022春•汉阳区期中）如图，在△ABC 中AB ＝AC ＝10，BC ＝16，若∠BAD ＝3∠DAC ，则CD ＝ ．【变式1-3】（2021秋•朝阳区校级期末）如图，在△ABC 中，∠C ＝90°，AB ＝30，D 是AC 上一点，AD ：CD ＝25：7，且DB ＝DA ，过AB 上一点P ，作PE ⊥AC 于E ，PF ⊥BD 于F ，则PE +PF 长是 ．【题型2 直角三角形中的分类讨论思想】【例2】（2022春•长沙月考）已知△ABC 中，AB ＝13，AC ＝15，BC 边上的高为12．则△ABC 的面积为（ ） A ．24或84B ．84C ．48或84D ．48【变式2-1】（2022春•宁津县期中）△ABC 中，AB ＝15，AC ＝13，高AD ＝12，则△ABC 的周长是（ ） A ．42B ．32C ．42或32D ．42或37【变式2-2】（2022春•香河县期中）已知直角三角形两边的长为5和12，则此三角形的周长为（ ） A ．30B ．√119+17C ．√119+17或30D ．36【变式2-3】（2022春•海淀区校级期中）在Rt △ABC 中，∠ACB ＝90°，AC ＝4，AB ＝5．点P 在直线AC 上，且BP ＝6，则线段AP 的长为 ．【题型3 勾股定理解勾股树问题】【例3】（2021秋•南关区期末）如图，所有阴影部分四边形都是正方形，所有三角形都是直角三角形，若正方形A、B、D的面积依次为6、10、24，则正方形C的面积为（）A．4B．6C．8D．12【变式3-1】（2021秋•高新区校级期末）如图，在四边形ABCD中，∠DAB＝∠BCD＝90°，分别以四边形的四条边为边向外作四个正方形，若S1+S4＝135，S3＝49，则S2＝（）A．184B．86C．119D．81【变式3-2】（2022春•泗水县期中）有一个边长为1的正方形，经过一次“生长”后，在它的左右肩上生出两个小正方形，其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了如图，如果继续“生长”下去，他将变得“枝繁叶茂”，请你计算出“生长”了2022次后形成的图形中所有正方形的面积之和为（）A．2020B．2021C．2022D．2023【变式3-3】（2022春•张湾区期中）如图①，在△ABC中，∠ACB＝90°，AC：BC＝4：3，这个直角三角形三边上分别有一个正方形．执行下面的操作：由两个小正方形向外分别作直角边之比为4：3的直角三角形，再分别以所得到的直角三角形的直角边为边长作正方形．图②是1次操作后的图形，图③是2次操作后的图形．如果图①中的直角三角形的周长为12，那么10次操作后的图形中所有正方形的面积和为（ ）A ．225B ．250C ．275D ．300【题型4 勾股定理解动点问题】【例4】（2021秋•开福区校级期末）如图，Rt △ACB 中，∠ACB ＝90°，AB ＝25cm ，AC ＝7cm ，动点P 从点B 出发沿射线BC 以2cm /s 的速度运动，设运动时间为ts ，当△APB 为等腰三角形时，t 的值为（ ）A ．62596或252B ．252或24或12C ．62596或24或12 D ．62596或252或24【变式4-1】（2021秋•宛城区期末）如图，在Rt △ABC 中，∠ACB ＝90°，BC ＝40cm ，AC ＝30cm ，动点P 从点B 出发沿射线BA 以2cm /s 的速度运动．则当运动时间t ＝ s 时，△BPC 为直角三角形．【变式4-2】（2022春•蚌山区校级期中）如图，在△ABC 中，∠ACB ＝90°，AB ＝10，AC ＝8，点P 从点A 出发，以每秒2个单位长度的速度沿折线A ﹣B ﹣C 运动．设点P 的运动时间为t 秒（t ＞0）． （1）BC 的长是 ．（2）当点P刚好在∠BAC的角平分线上时，t的值为．【变式4-3】（2022春•河东区期中）如图，已知△ABC中，∠B＝90°，AB＝16cm，BC＝12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，同时停止．（1）P、Q出发4秒后，求PQ的长；（2）当点Q在边CA上运动时，出发几秒钟后，△CQB能形成直角三角形？【题型5 勾股定理的验证】【例5】勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：将两个全等的直角三角形按图1所示摆放，其中∠DAB＝90°，求证：a2+b2＝c2证明：连接DB，过点D作BC边上的高DF，则DF＝EC＝b﹣a∵S四边形ADCB＝S△ACD+S△ABC=12b2+12ab．又∵S四边形ADCB＝S△ADB+S△DCB=12c2+12a（b﹣a）∴12b2+12ab=12c2+12a（b﹣a）∴a2+b2＝c2请参照上述证法，利用图2完成下面的证明．将两个全等的直角三角形按图2所示摆放，其中∠DAB＝90°．求证：a2+b2＝c2．【变式5-1】（2022春•巢湖市校级期中）学习勾股定理之后，同学们发现证明勾股定理有很多方法．某同学提出了一种证明勾股定理的方法：如图1点B是正方形ACDE边CD上一点，连接AB，得到直角三角形ACB，三边分别为a，b，c，将△ACB裁剪拼接至△AEF位置，如图2所示，该同学用图1、图2的面积不变证明了勾股定理．请你写出该方法证明勾股定理的过程．【变式5-2】（2021秋•朝阳区期末）【阅读理解】我国古人运用各种方法证明勾股定理，如图①，用四个直角三角形拼成正方形，通过证明可得中间也是一个正方形．其中四个直角三角形直角边长分别为a、b，斜边长为c．图中大正方形的面积可表示为（a+b）2，也可表示为c2+4×12ab，即（a+b）2＝c2+4×12ab，所以a2+b2＝c2．【尝试探究】美国第二十任总统伽菲尔德的“总统证法”如图②所示，用两个全等的直角三角形拼成一个直角梯形BCDE，其中△BCA≌△ADE，∠C＝∠D＝90°，根据拼图证明勾股定理．【定理应用】在Rt△ABC中，∠C＝90°，∠A、∠B、∠C所对的边长分别为a、b、c．求证：a2c2+a2b2＝c4﹣b4．【变式5-3】（2022春•寿光市期中）如图①，美丽的弦图，蕴含着四个全等的直角三角形．（1）弦图中包含了一大，一小两个正方形，已知每个直角三角形较长的直角边为a，较短的直角边为b，斜边长为c，结合图①，试验证勾股定理．（2）如图②，将这四个直角三角形紧密地拼接，形成飞镖状，已知外围轮廓（粗线）的周长为24，OC＝3，求该飞镖状图案的面积．（3）如图③，将八个全等的直角三角形紧密地拼接，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，若S1+S2+S3＝40，则S2＝．【题型6 直角三角形的判定】【例6】（2022春•绥宁县期中）若△ABC的三边长分别为a、b、c，下列条件中能判断△ABC是直角三角形的有（）①∠A＝∠B﹣∠C，②∠A：∠B：∠C＝3：4：5，③∠A＝90°﹣∠B，④∠A＝∠B=12∠C，⑤a2＝（b+c）（b﹣c），⑥a：b：c＝5：12：13．A．3个B．4个C．5个D．6个【变式6-1】（2022春•赣州月考）下列满足条件的三角形中，不是直角三角形的是（）A．在△ABC中，若a=35c，b=45c．则△ABC为直角三角形B．三边长的平方之比为1：2：3C．三内角之比为3：4：5D．三边长分别为a，b，c，c＝1+n2，a＝n2﹣1，b＝2n（n＞1）【变式6-2】（2022春•汉滨区期中）若△ABC的三边长a，b，c满足（a﹣c）2＝b2﹣2ac，则（）A．∠A为直角B．∠B为直角C．∠C为直角D．△ABC不是直角三角形【变式6-3】（2022春•开州区期中）下列是直角三角形的有（）个①△ABC中a2＝c2﹣b2②△ABC的三内角之比为3：4：7③△ABC的三边平方之比为1：2：3④三角形三边之比为3：4：5A．1B．2C．3D．4【题型7 勾股数问题】【例7】（2022春•滑县月考）在学习“勾股数”的知识时，小明发现了一组有规律的勾股数，并将它们记录在如下的表格中．a68101214…b815243548…c1017263750…则当a＝24时，b+c的值为（）A．162B．200C．242D．288【变式7-1】（2022•湖北）勾股定理最早出现在商高的《周髀算经》：“勾广三，股修四，经隅五”．观察下列勾股数：3，4，5；5，12，13；7，24，25；…，这类勾股数的特点是：勾为奇数，弦与股相差为1．柏拉图研究了勾为偶数，弦与股相差为2的一类勾股数，如：6，8，10；8，15，17；…，若此类勾股数的勾为2m（m≥3，m为正整数），则其弦是（结果用含m的式子表示）．【变式7-2】（2022春•白云区期末）（1）3k，4k，5k（k是正整数）是一组勾股数吗？如果是，请证明；如果不是，请说明理由；（2）如果a，b，c是一组勾股数，那么ak，bk，ck（k是正整数）也是一组勾股数吗？如果是，请证明；如果不是，请说明理由．【变式7-3】（2022•石家庄三模）已知：整式A＝n2+1，B＝2n，C＝n2﹣1，整式C＞0．（1）当n＝1999时，写出整式A+B的值（用科学记数法表示结果）；（2）求整式A2﹣B2；（3）嘉淇发现：当n取正整数时，整式A、B、C满足一组勾股数，你认为嘉淇的发现正确吗？请说明理由．【题型8 格点图中求角的度数】【例8】（2021秋•伊川县期末）如图，正方形ABCD是由9个边长为1的小正方形组成的，点E，F均在格点（每个小正方形的顶点都是格点）上，连接AE，AF，则∠EAF的度数是．【变式8-1】（2022•惠山区一模）如图所示的网格是由相同的小正方形组成的网格，点A，B，P是网格线的交点，则∠P AB+∠PBA＝°．【变式8-2】（2022春•武侯区校级期末）如图，在正方形网格中，每个小正方形的边长均为1，点A，B，C，D，P都在格点上，连接AP，CP，CD，则∠P AB﹣∠PCD＝．【变式8-3】（2022春•孝南区期中）如图所示的网格是正方形网格，△ABC和△CDE的顶点都是网格线交点，那么∠BCA+∠DCE＝．【题型9 勾股定理及其逆定理的运用】【例9】（2021秋•蓝田县校级期末）如图，在△ABC中，AB＝AC，D是CA的延长线上一点，连接BD．（1）若AC＝8，AD＝17，BD＝15，判断AB与BD的位置关系，并说明理由；（2）若∠D＝28°，∠DBC＝121°，求∠DAB的度数．【变式9-1】（2022春•陵城区期中）如图，在△ABC中，AD、BE分别为边BC、AC的中线，分别交BC、AC于点D、E．（1）若CD＝4，CE＝3，AB＝10，求证：∠C＝90°；（2）若∠C＝90°，AD＝6，BE＝8，求AB的长．【变式9-2】（2021春•当涂县期末）如图，在△ABC中．D是AB边的中点，DE⊥AB于点D，交AC于点E，且AE2﹣CE2＝BC2，（1）试说明：∠C＝90°；（2）若DE＝6，BD＝8，求CE的长．【变式9-3】（2022春•汉阳区校级月考）如图，在四边形ABCD中，∠ABC＝90°，AB＝6，BC＝8，CD ＝10，AD＝10√2．（1）求四边形ABCD的面积．（2）求对角线BD的长．。

沪科版八年级下册数学第18章勾股定理含答案一、单选题(共15题，共计45分)1、△ABC中，AB＝15，AC＝13，高AD＝12，则△ABC的周长是（）A.42B.32C.42或32D.42或372、如图，弧AD是以等边三角形ABC一边AB为半径的四分之一圆周，P为弧AD 上任意一点，若AC=5，则四边形ACBP周长的最大值是（）A.15B.15+5C.20D.15+53、下列各组线段中，不能构成直角三角形的是（）A.3，4，5B.5，12，13C.8，16，17D.7，24，254、下列各组数中能够作为直角三角形的三边长的是（）A.1，2，3B.2，3，4C.3，4，5D.4，5，65、连接一个几何图形上任意两点间的线段中，最长的线段称为这个几何图形的直径，根据此定义，图（扇形、菱形、直角梯形、红十字图标）中“直径”最小的是A. B. C. D.6、下列各组三条线段组成的三角形是直角三角形的是( ）A.1，1,B.2,3,4C.2，2,3D.6，8，117、如图，在平面直角坐标系中，正方形的顶点O与坐标原点重合，顶点A、C分别在x轴、y轴上，反比例函数的图象与正方形的两边、分别交于点M、N，轴，垂足为D，连接、、，下列结论错误的是①；②四边形与面积相等；③；④若，，则点C的坐标为.其中正确的结论有（）A.①②B.①②④C.②③④D.①②③④8、如图，在中，，，，垂足为D，，则BD的长为（）A. B.2 C. D.39、如图，在Rt△ABC中，∠C=90°，D为BC上一点，∠DAC=30°，BD=2，AB=2，则AC的长为（）A. B.2 C.3 D.10、下列长度的三条线段能组成钝角三角形的是( )A.3,4,4B.3,4,5C.3,4,6D.3,4,711、如图，正方形中，，E 是的中点，点 P 是对角线上一动点，则的最小值为（）A.4B.C.D.12、如图使用4个全等三角形与1个小正方形镶嵌而成的正方形图案已知大正方形面积为49，小正方形面积为4，若用x、y表示直角三角形的两直角边(x>y)，下列四个说法：①x2+y2=49；②x−y=2；③2xy+4=49；④x+y=9. 其中正确的是（）A.①②B.①②③C.①②④D.①②③④13、在Rt△ABC中，∠C=90°，AB=10，BC=6，则AC的长是（）A.8B.4C.64D.1614、若等腰三角形的腰长为13，底边长为10，则底边上的高为（）A.6B.7C.9D.1215、如图，在△ABC中，AC=BC，∠ACB=90°，点D在BC上，BD=3，DC=1，点P 是AB上的动点，则PC+PD的最小值为（）A.4B.5C.6D.7二、填空题(共10题，共计30分)16、如图，在2×2的正方形网格中四个小正方形的顶点叫格点，已经取定格点A和B，在余下的格点中任取一点C，使△ABC为直角三角形的概率是________．17、如图，在ABCD中，线段BE、CE分别平分∠ABC和∠BCD，若AB=5，BE=8，则CE的长度为________.18、如图，已知圆柱的底面直径,高,小虫在圆柱表面爬行，从点爬到点，然后在沿另一面爬回点，则小虫爬行的最短路程为________.19、如图，△ABC中，AB=AC，AB=5，BC=8，AD是∠BAC的平分线，则AD的长为________.20、如图，在Rt△ABC中，∠C＝90°，BC＝2 ，AC＝2，点D是BC的中点，点E是边AB上一动点，沿DE所在直线把△BDE翻折到△B′DE的位置，B′D 交AB于点F.若△AB′F为直角三角形，则AE的长为________或________21、平面直角坐标系中，点到原点的距离是________.22、如图，点P是y轴正半轴上一点，以P为圆心的圆与x轴、y轴分别交于点A、B、C、D，已知点A的坐标为，点C的坐标为，则点D的坐标为________．23、已知a、b、c是△ABC三边的长，且满足关系式，则△ABC的形状为________24、如图，已知△ABC的三个顶点均在格点上，则cosA的值为________.25、一座楼梯的示意图如图所示，BC是铅垂线，CA是水平线，AB，AC的夹角为θ（θ=30°）.要在楼梯上铺一条地毯，已知CA= cm，楼梯宽1 cm，则地毯的面积至少需要________平方米.三、解答题(共5题，共计25分)26、如图，方格纸上每个小正方形的面积为1．⑴在方格纸上，以线段AB为边画正方形ABCD，并计算所画正方形ABCD的面积．⑵请你在图上分别画出面积为5正方形A1B1C1D1和面积为10的正方形A 2B2C2D2，正方形的各个顶点都在方格纸的格点上．27、如图，在△ABC中，AB=AC，点E，F分别是边AB，AC的中点，点D在边BC 上．若DE=DF，AD=2，BC=6，求四边形AEDF的周长．28、如图，一根旗杆在离地面6米处折断，旗杆顶端落在离旗杆底部8米处，求旗杆折断之前有多高？29、如图，∠C=90°，AC=3，BC=4，AD=12，BD=13，试判断△ABD的形状，并说明理由.30、小明想知道学校旗杆的高，他发现旗杆上的绳子垂到地面还多了1m，当他把绳子的下端拉开5m后，发现下端刚好接触地面，求旗杆的高．参考答案一、单选题(共15题，共计45分)1、C2、B3、C4、C5、C6、A7、B8、C10、C11、B12、B13、A14、D15、B二、填空题(共10题，共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题，共计25分)26、27、28、29、30、。

沪科版八年级下册数学第18章勾股定理含答案一、单选题(共15题，共计45分)1、如图，以Rt△ABC的三边为直角边分别向外作等腰直角三角形．若AB=，则图中阴影部分的面积为（）A. B. C. D.52、下列四组数中，是勾股数的一组是（）A.3、5、7B. 、、C.5、12、13D.0.3、0.4、0.53、如图：在等腰梯形ABCD中，AD∥BC，过D作DF⊥BC于F，若AD＝2，BC＝4，DF＝2，则DC的长为（）A.1B.C.2D.4、如图所示是一个直角三角形的苗圃，由一个正方形花坛和两块直角三角形的草皮组成．如果两个直角三角形的两条斜边长分别为4米和6米，则草皮的总面积为（）平方米．A.3B.9C.12D.245、如图，CE，BF分别是△ABC的高线，连接EF，EF=6，BC=10，D、G分别是EF、BC的中点，则DG的长为（）A.6B.5C.4D.36、以下列各组数为三角形的三边，能构成直角三角形的是( )A.4，5，6B.1，1，C.6，8，11D.5，12，237、下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（）A. ，2，B.2，3，4C.6，7， 8D.3，4，58、三角形的三边长a，b，c满足2ab=（a+b）2﹣c2，则此三角形是（）A.钝角三角形B.锐角三角形C.直角三角形D.等边三角形9、如图，点O为平面直角坐标系的原点，点A在x轴上，△OAB是边长为4的等边三角形，以O为旋转中心，将△OAB按顺时针方向旋转60°，得到△OA′B′，那么点A′的坐标为( )A.(－2，2 )B.(－2，4)C.(－2，2 )D.(2，2 )10、以下列数组作为三角形的三条边长，其中能构成直角三角形的是( )A.1，，3B. ，，5C.1.5，2，2.5D. ，，11、如图，在长方形ABCD中，AB＝6，BC＝8，∠ABC的平分线交AD于点E，连接CE，过B点作BF⊥CE于点F，则BF的长为（）A. B. C. D.12、下列命题，假命题是（）A.有一个内角等于60°的等腰三角形是等边三角形B.有一个角是40°，腰相等的两个等腰三角形全等C.在直角三角形中，最大边的平方等于其他两边的平方和D.三角形两个内角平分线的交点到三边的距离相等13、已知直角三角形的两条边长分别是方程x2－14x+48=0的两个根，则此三角形的斜边长是（）A.10B.2C.10或2D.10或814、如图，直角△ABC的周长为24，且AB:AC=5:3，则BC=（）A.6B.8C.10D.1215、下列三角形中，不是直角三角形的是（）A.三个角的度数之比是1：2：3B.三条边长之比是1：2：  C.三条边长之比是1：2：4 D.三条边长之比是3：4：5二、填空题(共10题，共计30分)16、如图1，有一张矩形纸片ABCD，已知AB=10，AD=12，现将纸片进行如下操作：现将纸片沿折痕BF进行折叠，使点A落在BC边上的点E处，点F在AD 上（如图2）；然后将纸片沿折痕DH进行第二次折叠，使点C落在第一次的折痕BF上的点G处，点H在BC上（如图3），给出四个结论：①AF的长为10；②△BGH的周长为18；③= ；④GH的长为5，其中正确的结论有________．（写出所有正确结论的序号）17、南浔区某校在开展特色阳光大课间活动中融入了单脚跳跳球运动，如图1，当人单脚跳的过程中，小球会随着球杆绕着脚开始不停的旋转.大课间活动中，五位同学分别站在点处，处同学跳的时候，小球开始在地面上不停旋转形成，如图2为活动过程的俯视示意图，交于点G，，连结，当小球转到点时，，则球杆________ .18、如图，AB//CD，，E为BC上一点，且．若，，，则DE的长为________．19、如图，在Rt△ABC中，∠ACB=90°，AD平分∠CAB，交CB于点D，DE⊥AB，垂足为E．若AC=3，AB=5，则DE的长为________。

沪科版八年级下册数学第18章勾股定理含答案一、单选题(共15题，共计45分)1、如图：某港口P位于东西方向的海中线上，“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“选航”寻每小时航行15海里，“海天”号每小时流行12海里。

它们离开港口一个半小时后分别位于A，B处，至程距30海里。

如来知道“远航”号沿东北方向航行，那么∠BPN=（）度。

A.60B.45C.30D.无法确定2、已知一个直角三角形的两直角边长分别为3和4，则斜边长是（）A.5B.6C.7D.3、如图，矩形ABCD中，点G，E分别在边BC，DC上，连接AG，EG，AE，将△ABG和△ECG分别沿AG，EG折叠，使点B，C恰好落在AE上的同一点，记为点F．若CE＝3，CG＝4，则DE的长度为（）A. B. C.3 D.4、如图，在正方OABC中，点B的坐标是（4，4），点E、F分别在边BC，BA 上，.若，则点F的纵坐标是（）A.1B.C.2D.5、如图，矩形中，，，在数轴上，若以点A为圆心，对角线的长为半径作弧交数轴于点M，则点M表示的数为（）A. B. C. D.6、已知一个直角三角形的两边长分别为3和4，则第三边长是（）A.5B.4C.D.5或7、如图，在正方形中，，点在边上，且，将沿折叠得到，延长交边于点，则的长为（）A.2B.C.3D.8、下列四组线段中，可以构成直角三角形的是A.2，3，4B.3，4，5C.4，5，6D.7，8，99、下列各组数，可以作为直角三角形的三边长的是（）A.2，3，4B.7，24，25C.8，12，20D.5，13，1510、三个正方形按图示位置摆放，S表示面积，则S的大小为 ( )A.10B.500C.300D.3011、如图，每个小正方形的边长都为1，点A、B、C都在小正方形的顶点上，则∠ABC的正弦值为（）A.1B.C.D.12、三角形的三边分别为a、b、c，由下列条件不能判断它是直角三角形的是（）A. ，，B.C.D.13、在直角三角形中，两边长分别为3和4，则最长边的长度为（）A.5B.4C.5或D.5或414、以下列各组数据为三角形的三边，能构成直角三角形的是（）A.1cm，2cm，3cmB.2cm，2cm，2cmC.4cm，2cm，2cmD.cm，cm，1cm15、如图，PO是⊙O外一点，PA是⊙O的切线，PO=26cm，PA=24 cm，则⊙O的周长为（）A. B. C. D.二、填空题(共10题，共计30分)16、如图，C是以AB为直径的⊙O上一点，已知AB=10，BC=6，则圆心O到弦BC的距离是________．17、若抛物线y=x2﹣6x+c的顶点与原点的距离为5，则c的值为________．18、如图，x=________.19、一架长的梯子斜靠在一竖直的墙上，这时梯足距离墙底，如果梯子的顶端沿墙下滑，那么梯足将滑________ ：20、如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，将△ABC绕点A逆时针旋转得到△AB′C′，点B、C的对应点分别为点B'、C′，AB′与BC相交于点D，当B′C′∥AB时，则CD＝________．21、如图,长方体中, , , ,一只蚂蚁从点A出发,以4m/秒的速度沿长方体表面爬行到点C',至少需要________ 分钟.22、如图，在△ABC中，BC的垂直平分线MN交AB于点D，CD平分∠ACB.若AD ＝2，BD＝3，则AC的长为________.23、四个全等的直角三角形按图示方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为2的小正方形EFGH.已知AM为Rt△ABM较长直角边，AM ＝4 EF，则正方形ABCD的面积为________24、在Rt△ABC中，AC=9，BC=12，则AB=________．25、如图，先有一张矩形纸片，，，点，分别在矩形的边，上，将矩形纸片沿直线折叠，使点落在矩形的边上，记为点，点落在处，连接，交于点，连接.下列结论：① ；②四边形是菱形；③ ，重合时，；④ 的面积的取值范围是.其中正确的________；（把正确结论的序号都填上）.三、解答题(共5题，共计25分)26、在Rt△ABC 中，∠C＝90°，∠A、∠B、∠C 的对边分别为a、b、c．若a∶c＝15∶17，b＝24，求a.27、在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积．某学习小组经过合作交流，给出了下面的解题思路：作AD⊥BC于D，设BD=x，用含x的代数式表示CD→根据勾股定理，利用AD作为“桥梁”，列出方程求出x→再求出AD的长，从而计算三角形的面积．请你按照他们的解题思路完成解答过程．28、如图，在△ABC中，∠B 90°，AB 4，BC 2，以AC为边作△ACE，∠ACE 90°，AC=CE，延长BC至点D，使CD 5，连接DE．求证：△ABC∽△CED．29、在平面直角坐标系中，若△ABC的三个顶点的坐标分别为A（﹣4，1），B （﹣1，3），C（﹣4，3），求sinB的值．30、如图，将长AB=5cm，宽AD=3cm的长方形纸片ABCD折叠，使点A与C重合，折痕为EF，则AE长是多少？参考答案一、单选题(共15题，共计45分)1、B2、A3、B4、B5、C6、D7、C8、B9、B10、D11、D13、D14、D15、C二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、28、29、30、。

沪科版八年级下册数学第18章勾股定理含答案一、单选题(共15题，共计45分)1、如图所示,在数轴上点A所表示的数为a,则a的值为（）A.-1-B.1-C.-D.-1+2、如图，将矩形纸片沿直线折叠，使点C落在边的中点处，点B落在点处，其中，则的长为（）A. B.4 C.4.5 D.53、已知：如图，菱形ABCD的两条对角线相交于O，若AC=8，BD=6，则菱形ABCD的周长是（）A.20B.16C.12D.104、如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要多少米?（）A.4B.8C.9D.75、如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，连结CE 交AD于点F，连结BD交CE于点G，连结BE.下列结论：①CE＝BD；②△ADC是等腰直角三角形；③∠ADB＝∠AEB；④S＝BD·CE；⑤BC2＋DE2＝BE2四边形BCDE＋CD2.其中正确的结论有（）A.1个B.2个C.3个D.4个6、如图，D是△ABC内一点，BD⊥CD，AD＝6，BD＝4，CD＝3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是（）．A.7B.9C.10D.117、下面各组数中不能构成直角三角形三边长的一组数是（）A.3、4、5B.6、8、10C.5、12、13D.11、12、158、如图，有两棵树，一棵高5米，另一棵高2米，两树相距5米，一只小鸟从一棵树飞到另一棵树的树梢，至少飞了( )米。

A. 米B.5 米C.4米D. 米9、由线段a，b，c组成的三角形不是直角三角形的是（）A.a＝3，b＝4，c＝5B.a＝12，b＝13，c＝5C.a＝15，b＝8，c＝17 D.a＝13，b＝14，c＝1510、下列说法中正确的是（）A.已知a，b，c是三角形的三边，则a 2+b 2=c 2B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中，∠C=90°，所以a 2+b 2=c 2D.在Rt△ABC中，∠B=90°，所以a 2+b 2=c 211、如图，数轴上的点表示的数是-1，点表示的数是1，于点，且，以点为圆心，为半径画弧交数轴于点，则点表示的数为（）A. B. C.2.8 D.与AB切于点M，设12、．如图，半圆D的直径AB=4，与半圆O内切的动圆O1⊙O的半径为y，AM=x，则y关于x的函数关系式是( ) 1A.y=- x 2+xB.y=-x 2+xC.y=- x 2-xD.y= x 2-x13、如图，在△ABC中，∠ACB=90°，过B,C两点的⊙O交AC于点D，交AB于点E，连接EO并延长交⊙O于点F.连接BF,CF.若∠EDC=135°,CF= ,则AE2+BE2的值为（）A.8B.12C.16D.2014、将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB＝3，则BC的长为（）A.1B.2C.D.15、如图，在矩形片中，边，，将矩形片沿折叠，使点A与点C重合，折叠后得到的图形是图中阴影部分.给出下列结论：①四边形是菱形；② 的长是1.5；③ 的长为；④图中阴影部分的面积为5.5，其中正确的结论有（）A.1个B.2个C.3个D.4个二、填空题(共10题，共计30分)16、三角形两边长分别是8和6，第三边长是一元二次方程的一个实数根，则该三角形的面积是________．17、如图，扇形AOB的圆心角为直角，边长为1的正方形OCDE的顶点C，E，D 分别在OA，OB，上，过点A作AF⊥ED，交ED的延长线于点F，则图中阴影部分的面积等于________．18、如图，在等腰Rt△OAA1中，∠OAA1＝90°，OA＝1，以OA1为直角边作等腰Rt△OA1A2，以OA2为直角边作等腰Rt△OA2A3，…则OA8的长度为________.19、已知两条线段的长为3cm和4cm，当第三条线段的长为________时，这三条线段能组成一个直角三角形。