2017年中考数学专项复习《矩形(3)》练习(无答案) 浙教版

5.1 矩形2一．选择题1. 下列关于矩形的说法，正确的是（ ）A.对角线相等的四边形是矩形B.对角线互相平分的四边形是矩形C.矩形的对角线互相垂直且平分D.矩形的对角线相等且互相平分2. 下列各组条件中，能判定四边形ABCD 为矩形的是（ ）A.∠A+∠B=90° B ．AB∥CD，AB=CD ，AC=BD C.AB∥CD，AD=BC ，AC=BD D ．AC=BD ，∠A=90°3. 顺次连接四边形ABCD 的四条边的中点，得到一个矩形，那么（ ）A ．AC=BDB ．AC⊥BDC ．AB=CD D ．AB⊥CD4. 如图1，△ABC 中，AC 的垂直平分线分别交AC ．AB 于点D ．F ，BE⊥DF 交DF 的延长线于点E ，已知∠A=30°，BC=2，AF=BF ，则四边形BCDE 的面积是（ ）A ．2B ．3C ．4D ．45.（2015呼和浩特）如图2，矩形纸片ABCD ，AB=8，AD=6，将纸片折叠，使得AD 边落在AB 边上，折痕为AE ，再将△AED 沿DE 向右翻折，AE 与BC 的交点为F ，则△CEF 的面积为( )A. 12B. 98C. 2D. 4二．填空题6．（2014•娄底）如图3，要使平行四边形ABCD 是矩形，则应添加的条件是 （添加一个条件即可）．7. 如图4，四边形ABCD 中，对角线AC⊥BD，E ．F ．G ．H 分别是各边的中点，若AC=4cm ，BD=6cm ，则四边形EFGH 的面积是 cm 2．图1 图2 图 3图4 图58. 如图5所示，工人师傅做铝合金窗框分下面三个步骤进行：（1）先截出两对符合规格的铝合金窗料（如图①所示），使AB=CD，EF=GH．（2）摆放成如图②的四边形，则这时窗框的形状是_________，根据的数学道理是_________ ．（3）将直尺紧靠窗框的一个角（如图③），调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时（如图④，说明窗框合格，这时窗框是_________ ，根据的数学道理是_______ ．9. 如图6 在矩形ABCD中，M为AD边的中点，P为BC上一点，P E⊥MC，PF⊥MB，当AB．BC满足条件时，四边形PEMF为矩形．10. 如图7，Rt△ABC中，∠C=90°，AC=3，BC=4，点P为AB边上任一点，过P分别作PE⊥AC于E，PF⊥BC于F，则线段EF的最小值是．图6 图7 图8三．解答题11. （2014•四川巴中）如图8，在四边形ABCD中，点H是BC的中点，作射线AH，在线段AH及其延长线上分别取点E，F，连结BE，CF．（1）请你添加一个条件，使得△BEH≌△CFH，你添加的条件是，并证明．（2）在问题（1）中，当BH与EH满足什么关系时，四边形BFCE是矩形，请说明理由．12. 如图，在△ABC中，D是AB的中点．E是CD的中点，过点C作CF∥AB交AE的延长线于点F，连接BF．（1）求证：DB=CF；（2）如果AC=BC．试判断四边彤BDCF的形状．并证明你的结论．13. 如图，O是矩形ABCD的对角线的交点，E．F．G．H分别是OA．OB．OC．OD上的点，且AE=BF=CG=DH．（1）求证：四边形EFGH是矩形；（2）若E．F．G．H分别是OA．OB．OC．OD的中点，DG⊥AC，OF=2cm，求矩形ABCD的面积．5.1矩形21.D2.B3.B4.A5.C6.略7.68.略9. AB=BC 10.11.（1）EH=FH （2）BH=EH 12.（1）略 (2)矩形 13.（1）略（2）16cm2．。

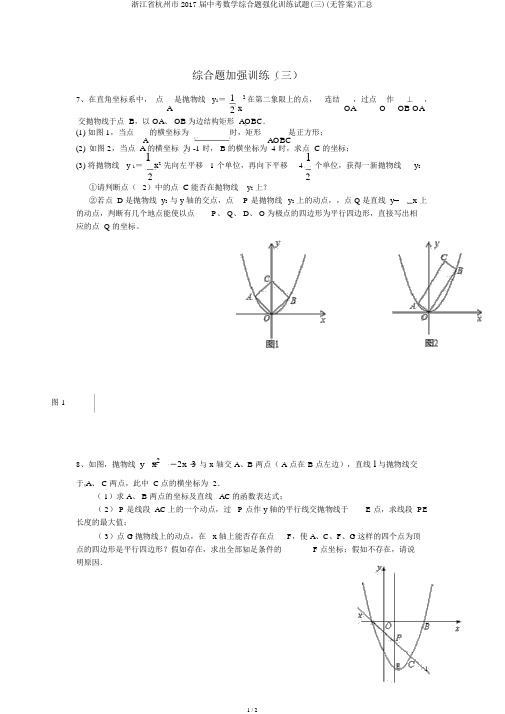
综合题加强训练（三）7、在直角坐标系中， 点A 是抛物线 y 1＝ 1x 2在第二象限上的点， 连结，过点 O 作 ⊥ ，2OAOB OA交抛物线于点 B ，以 OA 、 OB 为边结构矩形 AOBC ． (1) 如图 1，当点 A 的横坐标为时，矩形 是正方形；AOBC(2) 如图 2，当点 A 的横坐标 为 -1 时， B 的横坐标为 4 时，求点 C 的坐标；(3) 将抛物线 y 1＝ 1x 2先向左平移 1 个单位，再向下平移4 1个单位，获得一新抛物线y 222①请判断点（ 2）中的点 C 能否在抛物线 y 2 上？②若点 D 是抛物线 y 2 与 y 轴的交点，点 P 是抛物线 y 2 上的动点，，点 Q 是直线 y= x 上的动点，判断有几个地点能使以点 P 、 Q 、 D 、 O 为极点的四边形为平行四边形，直接写出相应的点 Q 的坐标。

图 18、如图，抛物线 y x 22x 3 与 x 轴交 A 、B 两点（ A 点在 B 点左边），直线 l 与抛物线交于 A 、 C 两点，此中 C 点的横坐标为 2．（ 1）求 A 、 B 两点的坐标及直线 AC 的函数表达式；（ 2） P 是线段 AC 上的一个动点，过 P 点作 y 轴的平行线交抛物线于E 点，求线段 PE长度的最大值；（ 3）点 G 抛物线上的动点，在 x 轴上能否存在点F ，使 A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形？假如存在，求出全部知足条件的F 点坐标；假如不存在，请说明原因．9、如图，在平面直角坐标系中，直线AB与 x 轴， y 轴分别交于点A（ 6， 0）， B（0， 8），点 C 的坐标为（ 0， m），过点 C 作 CE⊥ AB于点 E，点 D 为 x 轴上的一动点，连结CD， DE，以 CD， DE为边作□CDEF．（1）当 0＜ m＜ 8 时，求 CE的长（用含 m的代数式表示）；（2）当 m=3时，能否存在点D，使□CDEF的极点 F 恰巧落在 y 轴上？若存在，求出点 D 的坐标；若不存在，请说明原因；（3）点 D在整个运动过程中，若存在独一的地点，使得□CDEF为矩形，恳求出全部知足条件的 m的值．。

【巩固练习】一.选择题1.下列关于矩形的说法中正确的是( )A ．对角线相等的四边形是矩形B ．对角线互相平分的四边形是矩形C ．矩形的对角线互相垂直且平分D ．矩形的对角线相等且互相平分2. 矩形一个角的平分线分矩形一边为1cm 和3cm 两部分，则它的面积为（ ）A.32cmB. 42cmC. 122cmD. 42cm 或122cm 3.（2016春•青浦区期末）已知：如图，四边形ABCD 是平行四边形，延长BA 到点E ，使AE=AB ，联结ED ，EC ，AC ，添加一个条件，能使四边形ACDE 成为矩形的是（ ）A ．AC=CDB ．AB=ADC ．AD=AED ．BC=CE4. 把一张长方形的纸片按如图所示的方式折叠,EM 、FM 为折痕,折叠后的C 点落在B′M 或B′M 的延长线上,那么∠EMF 的度数是( )A.85°B.90°C.95°D.100°5．如图，四边形ABCD 中，AB ＝BC ，∠ABC ＝∠CDA ＝90°，BE ⊥AD 于点E ，且四边形ABCD 的面积为8，则BE ＝( )A.2B.3C.22D.326. 矩形的面积为1202cm ，周长为46cm ，则它的对角线长为（ ）A.15cmB.16cmC.17cmD.18cm二.填空题7．如图，四边形ABCD 是一张矩形纸片，AD ＝2AB ，若沿过点D 的折痕DE 将A 角翻折，使点A 落在BC 上的A 1处，则∠EA 1B ＝______°.8．如图，矩形ABCD中，AB＝2，BC＝3，对角线AC的垂直平分线分别交AD，BC于点E、F，连结CE，则CE的长______．9. 如图所示，矩形ABCD的两条对角线相交于点O，∠AOD＝120°，AB＝4cm，则矩形对角线AC长为________cm．10.（2016·黄冈）如图，在矩形ABCD中，点E、F分别在边CD、BC上，DC=3DE=3a，将矩形沿直线EF折叠，使点C恰好落在AD边上的点P处，则FP=_______.11.（2015•南漳县模拟）矩形ABCD的∠A的平分线AE分BC成两部分的比为1：3，若矩形ABCD的面积为36，则其周长为．12.如图所示，将矩形ABCD沿AE向上折叠，使点B落在DC边上的F处，若△AFD的周长为9，△ECF的周长为3，则矩形ABCD的周长为___________.三.解答题13．（2015•铁力市二模）如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E；PF ⊥CD于点F，连接EF，给出下列五个结论：①AP=EF；②AP⊥EF；③∠PFE=∠BAP；④PD=EC；⑤PB 2+PD 2=2PA 2，正确的有几个？14.已知：如图，四边形ABCD 的对角线AC 、BD 交于点O ，BE ⊥AC 于E ，DF ⊥AC 于F ，点O 既是AC 的中点，又是EF 的中点．（1）求证：△BOE ≌△DOF ；（2）若OA ＝12BD ，则四边形ABCD 是什么特殊四边形？说明理由．15.已知：如图，在矩形ABCD 中，E 、F 分别是边BC 、AB 上的点，且EF ＝ED ，EF ⊥ED ． 求证：AE 平分∠BAD ．【答案与解析】一.选择题1.【答案】D ；2.【答案】D ；【解析】矩形的短边可能是1，也可能是3，所以面积为4×1或4×3.3.【答案】D ；【解析】添加一个条件BC=CE.理由：∵四边形ABCD 为平行四边形，∴AB ∥CD 且AB=CD ，∵AE=AB ，∴AE ∥CD 且AE=CD ，∴四边形DEAC 为平行四边形，∵BC=EC ，AE=AB ，∴∠EAC=90°，∴平行四边形ACDE 是矩形.4.【答案】B ； 【解析】∠EMF＝∠EMB′＋∠FMB′＝21∠BMC′＋21∠CMC′＝21×180°＝90°. 5．【答案】C ；【解析】过点C 做BE 垂线，垂足为F ，易证△BAE ≌△CBF ，所以BF ＝AE ，BE ＝CF ，所以总面积＝AE ×BE ＋CF ×EF ＝ AE ×BE ＋BE ×（BE －AE ）＝28BE =，BE =6.【答案】C ；【解析】设边长为a b 、，则23,120,a b ab +==解得22289a b +=，所以对角线为17=.二.填空题7．【答案】60°；【解析】AD ＝A 1D ＝2CD ，所以∠CA 1D ＝30°，∠EA 1B ＝60°.8.【答案】136； 【解析】设AE ＝CE ＝x ，DE ＝3x -，()22232x x =-+，136x =. 9.【答案】8；【解析】由矩形的性质可知△AOB 是等边三角形，∴ AC ＝2AO ＝2AB ＝8cm ．10.【答案】；【解析】作FM ⊥AD 于M ，如图所示：则MF=DC=3a ，由题意可得：CE=2a ，由折叠可得：PE=CE=2a =2DE ，∠EPF=∠C=90°，∴∠DPE=30°，∴∠MPF=60°，∠MFP=30°，∴2=. 11.【答案】30或10；【解析】∵AE 平分∠DAB ，∴∠DAE=∠EAB ，∵四边形ABCD 是矩形，∴AD=BC ，DC=AB ，AD ∥BC ，∴∠DEA=∠BEA ，∴∠EAB=∠BEA ，∴AB=BE ，①设BE=x ，CE=3x ，则AD=4x ，AB=x ，∵矩形ABCD 的面积为36，∴x•4x=36，解得：x=3（舍负），即AD=BC=4x=12，AB=CD=x=3，∴矩形的周长为：AB+BC+CD+AD=2×（3+12）=30；②设BE=3x ，CE=x ，则AD=4x ，AB=3x ，∵矩形ABCD 的面积为36，∴3x•4x=36，解得：x=（舍负），即AD=BC=4x=4，AB=CD=x=，∴矩形的周长为：AB+BC+CD+AD=2×（4+）=10；故答案为：30或10．12.【答案】12；【解析】设BE ＝EF ＝x ，CE ＝b ，CF ＝a ，DF ＝y ，则9,3x b y y a x a b ++++=++=，解得3y =，矩形ABCD 的周长＝()()223312y a x b +++=⨯+=.三.解答题13.【解析】解：①正确，连接PC ，可得PC=EF ，PC=PA ，∴AP=EF ；②正确；延长AP ，交EF 于点N ，则∠EPN=∠BAP=∠PCE=∠PFE ，可得AP ⊥EF ；③正确；∠PFE=∠PCE=∠BAP ；④错误，PD=PF=CE ；⑤正确，PB 2+PD 2=2PA 2．所以正确的有4个：①②③⑤.14.【解析】（1）证明：∵BE ⊥AC ．DF ⊥AC ，∴∠BEO ＝∠DFO ＝90°，∵点O 是EF 的中点，∴OE ＝OF ，又∵∠DOF ＝∠BOE ，∴△BOE ≌△DOF （ASA ）；（2）解：四边形ABCD 是矩形．理由如下：∵△BOE ≌△DOF ，∴OB ＝OD ，又∵OA＝OC，∴四边形ABCD是平行四边形，∵OA＝12BD，OA＝12AC，∴BD＝AC，∴ABCD是矩形．15.【解析】证明：∵四边形ABCD是矩形，∴∠B＝∠C＝∠BAD＝90°，AB＝CD，∴∠BEF＋∠BFE＝90°．∵EF⊥ED，∴∠BEF＋∠CED＝90°．∴∠BFE＝∠CED．又∵EF＝ED，∴△EBF≌△DCE．∴BE＝CD．∴BE＝AB．∴∠BAE＝∠BEA＝45°．∴∠EAD＝45°．∴∠BAE＝∠EAD．∴AE平分∠BAD．。

2017年中考数学专项复习《一元二次方程的应用（3）》练习（无答案）浙教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017年中考数学专项复习《一元二次方程的应用（3）》练习（无答案）浙教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017年中考数学专项复习《一元二次方程的应用（3）》练习（无答案）浙教版的全部内容。

一元二次方程的应用(03)一、选择题1．从一块正方形的木板上锯掉2m宽的长方形木条，剩下的面积是48m2，则原来这块木板的面积是（）A．100m2B．64m2C．121m2D．144m22．要组织一次篮球联赛，赛制为单循环形式（每两队之间都赛一场）,计划安排21场比赛，则参赛球队的个数是( ）A．5个B．6个C．7个D．8个3．用一条长为40cm的绳子围成一个面积为acm2的长方形，a的值不可能为（）A．20 B．40 C．100 D．120二、填空题4．如图，一块四周镶有宽度相等的花边的长方形十字绣，它的长为120cm，宽为80cm,如果十字绣中央长方形图案的面积为6000cm2，则花边宽为．5．一块矩形菜地的面积是120m2，如果它的长减少2m,那么菜地就变成正方形，则原菜地的长是m．6．某小区2013年绿化面积为2000平方米，计划2015年绿化面积要达到2880平方米．如果每年绿化面积的增长率相同，那么这个增长率是．7．某商品经过连续两次降价,销售单价由原来的125元降到80元,则平均每次降价的百分率为．8．如图，在Rt△ABC中，∠BAC=90°，AB=AC=16cm，AD为BC边上的高．动点P从点A出发，沿A→D方向以cm/s的速度向点D运动．设△ABP的面积为S1，矩形PDFE的面积为S2，运动时间为t秒（0＜t＜8），则t= 秒时,S1=2S2．三、解答题9．随着铁路客运量的不断增长,重庆火车北站越来越拥挤，为了满足铁路交通的快速发展，该火车站去年开始启动了扩建工程，其中某项工程，甲队单独完成所需时间比乙队单独完成所需时间多5个月,并且两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的6倍．（1）求甲、乙两队单独完成这项工程各需几个月?（2）若甲队每月的施工费为100万元，乙队每月的施工费比甲队多50万元．在保证工程质量的前提下，为了缩短工期，拟安排甲、乙两队分工合作完成这项工程并且甲、乙两队的工作效率与题干的不同，在完成这项工程中，甲队施工时间是乙队施工时间的2倍,那么，甲队最多施工几个月才能使工程款不超过1500万元?（甲、乙两队的施工时间按月取整数）10．小丽为校合唱队购买某种服装时,商店经理给出了如下优惠条件：如果一次性购买不超过10件，单价为80元;如果一次性购买多于10件,那么每增加1件，购买的所有服装的单价降低2元,但单价不得低于50元．按此优惠条件，小丽一次性购买这种服装付了1200元．请问她购买了多少件这种服装?11．有一人患了流感，经过两轮传染后共有64人患了流感．（1)求每轮传染中平均一个人传染了几个人？(2）如果不及时控制，第三轮将又有多少人被传染？12．电动自动车已成为市民日常出行的首选工具．据某市某品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月份销售216辆．（1)求该品牌电动自行车销售量的月均增长率；（2）若该品牌电动自行车的进价为2300元，售价为2800元，则该经销商1至3月共盈利多少元?13．某新建火车站站前广场需要绿化的面积为46000米2，施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍，结果提前4天完成了该项绿化工程．（1）该项绿化工程原计划每天完成多少米2?（2）该项绿化工程中有一块长为20米，宽为8米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道（如图所示），问人行通道的宽度是多少米？14．某工厂一种产品2013年的产量是100万件，计划2015年产量达到121万件．假设2013年到2015年这种产品产量的年增长率相同．（1)求2013年到2015年这种产品产量的年增长率；（2）2014年这种产品的产量应达到多少万件？15．随着市民环保意识的增强，烟花爆竹销售量逐年下降．咸宁市2011年销售烟花爆竹20万箱，到2013年烟花爆竹销售量为9。

浙教版八年级下册数学矩形练习一、选择题1．矩形具有而一般平行四边形不具有的性质是（ ）A．对角线相等B．对角相等C．对边相等D．对角线互相平分2．如图，用一根绳子检查一平行四边形书架的侧边是否和上、下底都垂直，只需要用绳子分别测量比较书架的两条对角线AC，BD就可以判断，其推理依据是（ ）A．矩形的对角线相等B．矩形的四个角是直角C．对角线相等的四边形是矩形D．对角线相等的平行四边形是矩形3．如图，在矩形ABCD中，AO=5，CD=6，则AD的长为（ ）A．5B．6C．7D．84．如图，在矩形ABCD中，对角线AC、BD相交于点O，DE⊥AC于点E，∠EDC：∠EDA=1：2，且DE=23，则AC的长度是（ ）A．25B．2C．8D．5335．如图，将矩形ABCD沿对角线AC折叠，B的对应点为E，AE与CD相交于点F.若∠FCE=40°，则∠CAB的度数为（ ）A．15°B．20°C．25°D．40°6．如图，在▱ ABCD中，有下列条件：①AC=BD.②∠1+∠3=90°.③OB= 1AC.④∠1=∠2.其中能判定2▱ ABCD是矩形的有（ ）A．①B．①②③C．②③④D．①②③④7．如图，矩形ABCD中，AB=5，AD=6，点P为平面内一点，且BP=2，点Q为CD上一个动点，则AQ+PQ的最小值为（ ）A．11B．52−2C．103−2D．138．已知，矩形ABCD中，AB=8，BC=6，点E是线段AB上的一个动点，将线段DE绕点D逆时针旋转90°得到DF，过F作FG⊥CD于点G，连接EF，取EF的中点H，连接DH，AH．点E在运动过程中，下列结论：①△ADE≌△GDF；②当点H和点G互相重合时，AE=6；③∠GFH=∠ADE；④32≤AH≤72．正确的有（ ）个．A．1B．2C．3D．4二、填空题9．如图，已知▱ABCD中对角线AC，BD相交于点O，请你添加一个适当的条件，使▱ABCD成为一个矩形．你添加的条件是__．10．已知矩形的面积是43，其中一边长为6，则对角线长为 ．11．如图．将矩形ABCD沿直线DE折叠，顶点A落在BC边上F处，已知BE＝3，CD＝8．则BF的长是 ．12．如图，已知矩形ABCD，AB=9，AD=4，E为CD边上一点，CE=6，点P从B点出发，以每秒1个单位的速度沿着BA边向终点A运动，连接PE，设点P运动的时间为t秒，则当t的值为 时，△PAE是以PE为腰的等腰三角形．三、解答题13．如图，在▱ABCD中，AE⊥BC于E，点F在边AD上，BE=DF，求证：四边形AECF是矩形.14．如图，四边形ABCD是矩形，把矩形沿对角线AC折叠，点B落在点E处，CE与AD相交于点O．（1）求证∶AO=CO（2）若∠OCD=30∘，AB=3，求△AOC的面积．15．如图，在△ABC中，AC=9，AB=12，BC=15，P 为边BC上一动点，PG⊥AC 于点G，PH⊥AB 于点H.（1）求证：四边形AGPH 是矩形.（2）在点P 的运动过程中，GH 的长是否存在最小值? 若存在，请求出最小值；若不存在，请说明理由.答案解析部分1．【答案】A【解析】【分析】矩形是一个特殊的平行四边形，因此平行四边形的性质矩形都具有，而矩形的性质：①对角线相等，②四个角是直角平行四边形不具有，据此即可得到结果。

浙教新版八年级下学期《5.1 矩形》同步练习卷一．选择题（共21小题）1．如图，矩形ABCD中，AB＝3，BC＝4，EB∥DF且BE与DF之间的距离为3，则AE的长是（）A．B．C．D．2．如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于E、F，连接PB、PD．若AE＝2，PF＝8．则图中阴影部分的面积为（）A．10B．12C．16D．183．如图，已知点P是矩形ABCD内一点（不含边界），设∠P AD＝θ1，∠PBA＝θ2，∠PCB＝θ3，∠PDC＝θ4，若∠APB＝80°，∠CPD＝50°，则（）A．（θ1+θ4）﹣（θ2+θ3）＝30°B．（θ2+θ4）﹣（θ1+θ3）＝40°C．（θ1+θ2）﹣（θ3+θ4）＝70°D．（θ1+θ2）+（θ3+θ4）＝180°4．矩形ABCD与CEFG如图放置，点B，C，E共线，点C，D，G共线，连接AF，取AF的中点H，连接GH．若BC＝EF＝2，CD＝CE＝1，则GH＝（）A．1B．C．D．5．如图，在平面直角坐标系中，矩形OABC的两边OA，OC分别在x轴和y轴上，并且OA＝5，OC＝3．若把矩形OABC绕着点O逆时针旋转，使点A恰好落在BC边上的A1处，则点C的对应点C1的坐标为（）A．（﹣，）B．（﹣，）C．（﹣，）D．（﹣，）6．如图，在矩形ABCD中，点E是边BC的中点，AE⊥BD，垂足为F，则tan ∠BDE的值是（）A．B．C．D．7．如图，将矩形纸片ABCD沿直线EF折叠，使点C落在AD边的中点C′处，点B落在点B′处，其中AB＝9，BC＝6，则FC′的长为（）A．B．4C．4.5D．58．如图，已知矩形ABCD的顶点A，D分别落在x轴、y轴上，OD＝2OA＝6，AD：AB＝3：1，则点C的坐标是（）A．（2，7）B．（3，7）C．（3，8）D．（4，8）9．在探索“尺规三等分角”这个数学名题的过程中，曾利用了如图，该图中，四边形ABCD是矩形，E是BA延长线上一点，F是CE上一点，∠ACF＝∠AFC，∠F AE＝∠FEA．若∠ACB＝21°，则∠ECD的度数是（）A．7°B．21°C．23°D．24°10．如图，在矩形ABCD中，AB＝2，BC＝3．若点E是边CD的中点，连接AE，过点B作BF⊥AE交AE于点F，则BF的长为（）A．B．C．D．11．如图，点O是矩形ABCD的对角线AC的中点，OM∥AB交AD于点M，若OM＝3，BC＝10，则OB的长为（）A．5B．4C．D．12．已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（）A．∠A＝∠B B．∠A＝∠C C．AC＝BD D．AB⊥BC 13．已知平行四边形ABCD，AC、BD是它的两条对角线，那么下列条件中，能判断这个平行四边形为矩形的是（）A．∠BAC＝∠DCA B．∠BAC＝∠DAC C．∠BAC＝∠ABD D．∠BAC＝∠ADB14．在△ABC中，点D是边BC上的点（与B，C两点不重合），过点D作DE ∥AC，DF∥AB，分别交AB，AC于E，F两点，下列说法正确的是（）A．若AD⊥BC，则四边形AEDF是矩形B．若AD垂直平分BC，则四边形AEDF是矩形C．若BD＝CD，则四边形AEDF是菱形D．若AD平分∠BAC，则四边形AEDF是菱形15．下列关于矩形的说法中正确的是（）A．对角线相等的四边形是矩形B．矩形的对角线相等且互相平分C．对角线互相平分的四边形是矩形D．矩形的对角线互相垂直且平分16．如图，在矩形ABCD中，对角线AC，BD相交于点O，∠AOB＝60°，AC ＝6cm，则AB的长是（）A．3cm B．6cm C．10cm D．12cm17．如图，矩形ABCD的对角线AC与BD相交于点O，∠ADB＝30°，AB＝4，则OC＝（）A．5B．4C．3.5D．318．如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若AC＝4，则四边形OCED的周长为（）A．4B．8C．10D．1219．如图，矩形ABCD的对角线AC与BD相交于点O，CE∥BD，DE∥AC，AD ＝2，DE＝2，则四边形OCED的面积为（）A．2B．4C．4D．820．矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），D是OA的中点，点E在AB上，当△CDE的周长最小时，点E的坐标为（）A．（3，1）B．（3，）C．（3，）D．（3，2）21．如图，矩形ABCD中，AD＝2，AB＝3，过点A，C作相距为2的平行线段AE，CF，分别交CD，AB于点E，F，则DE的长是（）A．B．C．1D．二．填空题（共10小题）22．如图，矩形OABC的顶点A，C分别在坐标轴上，B（8，7），D（5，0），点P是边AB或边BC上的一点，连接OP，DP，当△ODP为等腰三角形时，点P的坐标为．23．如图，矩形EFGH的四个顶点分别在矩形ABCD的各条边上，AB＝EF，FG ＝2，GC＝3．有以下四个结论：①∠BGF＝∠CHG；②△BFG≌△DHE；③tan∠BFG＝；④矩形EFGH的面积是4．其中一定成立的是．（把所有正确结论的序号填在横线上）24．如图，在矩形ABCD中，AB＝4，AD＝2，点E在CD上，DE＝1，点F是边AB上一动点，以EF为斜边作Rt△EFP．若点P在矩形ABCD的边上，且这样的直角三角形恰好有两个，则AF的值是．25．对于一个位置确定的图形，如果它的所有点都在一个水平放置的矩形内部或边上，且该图形与矩形的每条边都至少有一个公共点（如图1），那么这个矩形水平方向的边长称为该图形的宽，铅锤方向的边长称为该矩形的高．如图2，菱形ABCD的边长为1，边AB水平放置．如果该菱形的高是宽的，那么它的宽的值是．26．如图，平面直角坐标系中，矩形OABC的顶点A（﹣6，0），C（0，2）．将矩形OABC绕点O顺时针方向旋转，使点A恰好落在OB上的点A1处，则点B的对应点B1的坐标为．27．如图，E、F，G、H分别为矩形ABCD的边AB、BC、CD、DA的中点，连接AC、HE、EC，GA，GF．已知AG⊥GF，AC＝，则AB的长为．28．如图，矩形ABCD的对角线AC与BD相交点O，AC＝10，P、Q分别为AO、AD的中点，则PQ的长度为．29．如图，在平行四边形ABCD中，添加一个条件，使平行四边形ABCD 是矩形．30．如图，在矩形ABCD中，点E是CD的中点，点F是BC上一点，且FC＝2BF，连接AE，EF．若AB＝2，AD＝3，则cos∠AEF的值是．31．如图，在矩形ABCD中，∠ABC的平分线交AD于点E，连接CE．若BC ＝7，AE＝4，则CE＝．三．解答题（共19小题）32．如图，在矩形ABCD中，E是AB的中点，连接DE、CE．（1）求证：△ADE≌△BCE；（2）若AB＝6，AD＝4，求△CDE的周长．33．在矩形ABCD中，点E在BC上，AE＝AD，DF⊥AE，垂足为F．（1）求证：DF＝AB；（2）若∠FDC＝30°，且AB＝4，求AD．34．如图，矩形ABCD中，E是AD的中点，延长CE，BA交于点F，连接AC，DF．（1）求证：四边形ACDF是平行四边形；（2）当CF平分∠BCD时，写出BC与CD的数量关系，并说明理由．35．如图，在△ABC中，点O是边AC上一个动点，过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F．（1）若CE＝8，CF＝6，求OC的长；（2）连接AE、AF．问：当点O在边AC上运动到什么位置时，四边形AECF 是矩形？并说明理由．36．如图，在▱ABCD中，点O是边BC的中点，连接DO并延长，交AB延长线于点E，连接BD，EC．（1）求证：四边形BECD是平行四边形；（2）若∠A＝50°，则当∠BOD＝°时，四边形BECD是矩形．37．如图，在四边形ABCD中，AD∥BC，∠ABC＝90°，AB＝AD，连接BD，点E在AB上，且∠BDE＝15°，DE＝4，DC＝2．（1）求BE的长；（2）求四边形DEBC的面积．（注意：本题中的计算过程和结果均保留根号）38．如图，在菱形ABCD中，对角线AC与BD交于点O．过点C作BD的平行线，过点D作AC的平行线，两直线相交于点E．（1）求证：四边形OCED是矩形；（2）若CE＝1，DE＝2，则菱形ABCD的面积是．39．如图，在矩形ABCD，AD＝AE，DF⊥AE于点F．求证：AB＝DF．40．如图，在矩形ABCD中，对角线AC的垂直平分线EF分别交AD、AC、BC 于点E、O、F，连接CE和AF．（1）求证：四边形AECF为菱形；（2）若AB＝4，BC＝8，求菱形AECF的周长．41．如图，在矩形ABCD中，E是AD上一点，PQ垂直平分BE，分别交AD、BE、BC于点P、O、Q，连接BP、EQ．（1）求证：四边形BPEQ是菱形；（2）若AB＝6，F为AB的中点，OF+OB＝9，求PQ的长．42．如图，已知BA＝AE＝DC，AD＝EC，CE⊥AE，垂足为E．（1）求证：△DCA≌△EAC；（2）只需添加一个条件，即，可使四边形ABCD为矩形．请加以证明．43．如图，DB∥AC，且DB＝AC，E是AC的中点，（1）求证：BC＝DE；（2）连接AD、BE，若要使四边形DBEA是矩形，则需给△ABC添加什么条件，为什么？44．如图，将▱ABCD的边AB延长到点E，使BE＝AB，连接DE，交边BC于点F．（1）求证：△BEF≌△CDF；（2）连接BD、CE，若∠BFD＝2∠A，求证：四边形BECD是矩形．45．如图，矩形ABCD的对角线AC，BD相交于点O，点E，F在BD上，BE ＝DF．（1）求证：AE＝CF；（2）若AB＝6，∠COD＝60°，求矩形ABCD的面积．46．如图，在矩形ABCD中，连接对角线AC、BD，将△ABC沿BC方向平移，使点B移到点C，得到△DCE．（1）求证：△ACD≌△EDC；（2）请探究△BDE的形状，并说明理由．47．如图，矩形ABCD中，∠ABD、∠CDB的平分线BE、DF分别交边AD、BC 于点E、F．（1）求证：四边形BEDF是平行四边形；（2）当∠ABE为多少度时，四边形BEDF是菱形？请说明理由．48．如图，矩形ABCD中，AB＝6，BC＝4，过对角线BD中点O的直线分别交AB，CD边于点E，F．（1）求证：四边形BEDF是平行四边形；（2）当四边形BEDF是菱形时，求EF的长．49．如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．（1）求证：四边形AECF是菱形；（2）若AB＝，∠DCF＝30°，求四边形AECF的面积．（结果保留根号）50．如图，在矩形ABCD中，E、F分别是边AB、CD的中点，连接AF，CE．（1）求证：△BEC≌△DF A；（2）求证：四边形AECF是平行四边形．浙教新版八年级下学期《5.1 矩形》2018年同步练习卷参考答案与试题解析一．选择题（共21小题）1．如图，矩形ABCD中，AB＝3，BC＝4，EB∥DF且BE与DF之间的距离为3，则AE的长是（）A．B．C．D．【分析】过点D作DG⊥BE，垂足为G，则GD＝3，首先证明△AEB≌△GED，由全等三角形的性质可得到AE＝EG，设AE＝EG＝x，则ED＝4﹣x，在Rt △DEG中依据勾股定理列方程求解即可．【解答】解：如图所示：过点D作DG⊥BE，垂足为G，则GD＝3．∵∠A＝∠G，∠AEB＝∠GED，AB＝GD＝3，∴△AEB≌△GED．∴AE＝EG．设AE＝EG＝x，则ED＝4﹣x，在Rt△DEG中，ED2＝GE2+GD2，x2+32＝（4﹣x）2，解得：x＝．故选：C．【点评】本题主要考查的是矩形的性质、勾股定理的应用，依据题意列出关于x 的方程是解题的关键．2．如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于E、F，连接PB、PD．若AE＝2，PF＝8．则图中阴影部分的面积为（）A．10B．12C．16D．18【分析】想办法证明S△PEB ＝S△PFD解答即可．【解答】解：作PM⊥AD于M，交BC于N．则有四边形AEPM，四边形DFPM，四边形CFPN，四边形BEPN都是矩形，∴S△ADC ＝S△ABC，S△AMP＝S△AEP，S△PBE＝S△PBN，S△PFD＝S△PDM，S△PFC＝S△PCN，∴S△DFP ＝S△PBE＝×2×8＝8，∴S阴＝8+8＝16，故选：C．【点评】本题考查矩形的性质、三角形的面积等知识，解题的关键是证明S△PEB＝S△PFD．3．如图，已知点P是矩形ABCD内一点（不含边界），设∠P AD＝θ1，∠PBA＝θ2，∠PCB＝θ3，∠PDC＝θ4，若∠APB＝80°，∠CPD＝50°，则（）A．（θ1+θ4）﹣（θ2+θ3）＝30°B．（θ2+θ4）﹣（θ1+θ3）＝40°C．（θ1+θ2）﹣（θ3+θ4）＝70°D．（θ1+θ2）+（θ3+θ4）＝180°【分析】依据矩形的性质以及三角形内角和定理，可得∠ABC＝θ2+80°﹣θ1，∠BCD＝θ3+130°﹣θ4，再根据矩形ABCD中，∠ABC+∠BCD＝180°，即可得到（θ1+θ4）﹣（θ2+θ3）＝30°．【解答】解：∵AD∥BC，∠APB＝80°，∴∠CBP＝∠APB﹣∠DAP＝80°﹣θ1，∴∠ABC＝θ2+80°﹣θ1，又∵△CDP中，∠DCP＝180°﹣∠CPD﹣∠CDP＝130°﹣θ4，∴∠BCD＝θ3+130°﹣θ4，又∵矩形ABCD中，∠ABC+∠BCD＝180°，∴θ2+80°﹣θ1+θ3+130°﹣θ4＝180°，即（θ1+θ4）﹣（θ2+θ3）＝30°，故选：A．【点评】本题主要考查了矩形的性质以及三角形内角和定理的运用，解决问题的关键是掌握：矩形的四个角都是直角．4．矩形ABCD与CEFG如图放置，点B，C，E共线，点C，D，G共线，连接AF，取AF的中点H，连接GH．若BC＝EF＝2，CD＝CE＝1，则GH＝（）A．1B．C．D．【分析】延长GH交AD于点P，先证△APH≌△FGH得AP＝GF＝1，GH＝PH ＝PG，再利用勾股定理求得PG＝，从而得出答案．【解答】解：如图，延长GH交AD于点P，∵四边形ABCD和四边形CEFG都是矩形，∴∠ADC＝∠ADG＝∠CGF＝90°，AD＝BC＝2、GF＝CE＝1，∴AD∥GF，∴∠GFH＝∠P AH，又∵H是AF的中点，∴AH＝FH，在△APH和△FGH中，∵，∴△APH≌△FGH（ASA），∴AP＝GF＝1，GH＝PH＝PG，∴PD＝AD﹣AP＝1，∵CG＝2、CD＝1，∴DG＝1，则GH＝PG＝×＝，故选：C．【点评】本题主要考查矩形的性质，解题的关键是掌握全等三角形的判定与性质、矩形的性质、勾股定理等知识点．5．如图，在平面直角坐标系中，矩形OABC的两边OA，OC分别在x轴和y轴上，并且OA＝5，OC＝3．若把矩形OABC绕着点O逆时针旋转，使点A恰好落在BC边上的A1处，则点C的对应点C1的坐标为（）A．（﹣，）B．（﹣，）C．（﹣，）D．（﹣，）【分析】直接利用相似三角形的判定与性质得出△ONC1三边关系，再利用勾股定理得出答案．【解答】解：过点C1作C1N⊥x轴于点N，过点A1作A1M⊥x轴于点M，由题意可得：∠C1NO＝∠A1MO＝90°，∠1＝∠2＝∠3，则△A1OM∽△OC1N，∵OA＝5，OC＝3，∴OA1＝5，A1M＝3，∴OM＝4，∴设NO＝3x，则NC1＝4x，OC1＝3，则（3x）2+（4x）2＝9，解得：x＝±（负数舍去），则NO＝，NC1＝，故点C的对应点C1的坐标为：（﹣，）．故选：A．【点评】此题主要考查了矩形的性质以及勾股定理等知识，正确得出△A1OM∽△OC1N是解题关键．6．如图，在矩形ABCD中，点E是边BC的中点，AE⊥BD，垂足为F，则tan∠BDE的值是（）A．B．C．D．【分析】证明△BEF∽△DAF，得出EF＝AF，EF＝AE，由矩形的对称性得：AE＝DE，得出EF＝DE，设EF＝x，则DE＝3x，由勾股定理求出DF＝＝2x，再由三角函数定义即可得出答案．【解答】解：∵四边形ABCD是矩形，∴AD＝BC，AD∥BC，∵点E是边BC的中点，∴BE＝BC＝AD，∴△BEF∽△DAF，∴＝，∴EF＝AF，∴EF＝AE，∵点E是边BC的中点，∴由矩形的对称性得：AE＝DE，∴EF＝DE，设EF＝x，则DE＝3x，∴DF＝＝2x，∴tan∠BDE＝＝＝；故选：A．【点评】本题考查了相似三角形的判定和性质，矩形的性质，三角函数等知识；熟练掌握矩形的性质，证明三角形相似是解决问题的关键．7．如图，将矩形纸片ABCD沿直线EF折叠，使点C落在AD边的中点C′处，点B落在点B′处，其中AB＝9，BC＝6，则FC′的长为（）A．B．4C．4.5D．5【分析】设FC′＝x，则FD＝9﹣x，根据矩形的性质结合BC＝6、点C′为AD 的中点，即可得出C′D的长度，在Rt△FC′D中，利用勾股定理即可找出关于x的一元一次方程，解之即可得出结论．【解答】解：设FC′＝x，则FD＝9﹣x，∵BC＝6，四边形ABCD为矩形，点C′为AD的中点，∴AD＝BC＝6，C′D＝3．在Rt△FC′D中，∠D＝90°，FC′＝x，FD＝9﹣x，C′D＝3，∴FC′2＝FD2+C′D2，即x2＝（9﹣x）2+32，解得：x＝5．故选：D．【点评】本题考查了矩形的性质以及勾股定理，在Rt△FC′D中，利用勾股定理找出关于FC′的长度的一元一次方程是解题的关键．8．如图，已知矩形ABCD的顶点A，D分别落在x轴、y轴上，OD＝2OA＝6，AD：AB＝3：1，则点C的坐标是（）A．（2，7）B．（3，7）C．（3，8）D．（4，8）【分析】过C作CE⊥y轴于E，根据矩形的性质得到CD＝AB，∠ADC＝90°，根据余角的性质得到∠DCE＝∠ADO，根据相似三角形的性质得到CE＝OD＝2，DE＝OA＝1，于是得到结论．【解答】解：过C作CE⊥y轴于E，∵四边形ABCD是矩形，∴CD＝AB，∠ADC＝90°，∴∠ADO+∠CDE＝∠CDE+∠DCE＝90°，∴∠DCE＝∠ADO，∴△CDE∽△ADO，∴，∵OD＝2OA＝6，AD：AB＝3：1，∴OA＝3，CD：AD＝，∴CE＝OD＝2，DE＝OA＝1，∴OE＝7，∴C（2，7），故选：A．【点评】本题考查了矩形的性质，相似三角形的判定和性质，坐标与图形性质，正确的作出辅助线是解题的关键．9．在探索“尺规三等分角”这个数学名题的过程中，曾利用了如图，该图中，四边形ABCD是矩形，E是BA延长线上一点，F是CE上一点，∠ACF＝∠AFC，∠F AE＝∠FEA．若∠ACB＝21°，则∠ECD的度数是（）A．7°B．21°C．23°D．24°【分析】由矩形的性质得出∠BCD＝90°，AB∥CD，AD∥BC，证出∠FEA＝∠ECD，∠DAC＝∠ACB＝21°，由三角形的外角性质得出∠ACF＝2∠FEA，设∠ECD＝x，则∠ACF＝2x，∠ACD＝3x，由互余两角关系得出方程，解方程即可．【解答】解：∵四边形ABCD是矩形，∴∠BCD＝90°，AB∥CD，AD∥BC，∴∠FEA＝∠ECD，∠DAC＝∠ACB＝21°，∵∠ACF＝∠AFC，∠F AE＝∠FEA，∴∠ACF＝2∠FEA，设∠ECD＝x，则∠ACF＝2x，∴∠ACD＝3x，∴3x+21°＝90°，解得：x＝23°；故选：C．【点评】本题考查了矩形的性质、平行线的性质、直角三角形的性质、三角形的外角性质；熟练掌握矩形的性质和平行线的性质是解决问题的关键．10．如图，在矩形ABCD中，AB＝2，BC＝3．若点E是边CD的中点，连接AE，过点B作BF⊥AE交AE于点F，则BF的长为（）A．B．C．D．【分析】根据S△ABE ＝S矩形ABCD＝3＝•AE•BF，先求出AE，再求出BF即可．【解答】解：如图，连接BE．∵四边形ABCD是矩形，∴AB＝CD＝2，BC＝AD＝3，∠D＝90°，在Rt△ADE中，AE＝＝＝，∵S△ABE ＝S矩形ABCD＝3＝•AE•BF，∴BF＝．故选：B．【点评】本题考查矩形的性质、勾股定理、三角形的面积公式等知识，解题的关键是灵活运用所学知识解决问题，学会用面积法解决有关线段问题，属于中考常考题型．11．如图，点O是矩形ABCD的对角线AC的中点，OM∥AB交AD于点M，若OM＝3，BC＝10，则OB的长为（）A．5B．4C．D．【分析】已知OM是△ADC的中位线，再结合已知条件则DC的长可求出，所以利用勾股定理可求出AC的长，由直角三角形斜边上中线的性质则BO的长即可求出．【解答】解：∵四边形ABCD是矩形，∴∠D＝90°，∵O是矩形ABCD的对角线AC的中点，OM∥AB，∴OM是△ADC的中位线，∵OM＝3，∴DC＝6，∵AD＝BC＝10，∴AC＝＝2，∴BO＝AC＝，故选：D．【点评】本题考查了矩形的性质，勾股定理的运用，直角三角形斜边上中线的性质以及三角形的中位线的应用，解此题的关键是求出AC的长．12．已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（）A．∠A＝∠B B．∠A＝∠C C．AC＝BD D．AB⊥BC【分析】由矩形的判定方法即可得出答案．【解答】解：A、∠A＝∠B，∠A+∠B＝180°，所以∠A＝∠B＝90°，可以判定这个平行四边形为矩形，正确；B、∠A＝∠C不能判定这个平行四边形为矩形，错误；C、AC＝BD，对角线相等，可推出平行四边形ABCD是矩形，故正确；D、AB⊥BC，所以∠B＝90°，可以判定这个平行四边形为矩形，正确；故选：B．【点评】本题主要考查的是矩形的判定定理．但需要注意的是本题的知识点是关于各个图形的性质以及判定．13．已知平行四边形ABCD，AC、BD是它的两条对角线，那么下列条件中，能判断这个平行四边形为矩形的是（）A．∠BAC＝∠DCA B．∠BAC＝∠DAC C．∠BAC＝∠ABD D．∠BAC＝∠ADB【分析】由矩形和菱形的判定方法即可得出答案．【解答】解：A、∠BAC＝∠DCA，不能判断四边形ABCD是矩形；B、∠BAC＝∠DAC，能判定四边形ABCD是菱形；不能判断四边形ABCD是矩形；C、∠BAC＝∠ABD，能得出对角线相等，能判断四边形ABCD是矩形；D、∠BAC＝∠ADB，不能判断四边形ABCD是矩形；故选：C．【点评】本题考查了矩形的判定、平行四边形的性质、菱形的判定；熟练掌握矩形的判定是解决问题的关键．14．在△ABC中，点D是边BC上的点（与B，C两点不重合），过点D作DE ∥AC，DF∥AB，分别交AB，AC于E，F两点，下列说法正确的是（）A．若AD⊥BC，则四边形AEDF是矩形B．若AD垂直平分BC，则四边形AEDF是矩形C．若BD＝CD，则四边形AEDF是菱形D．若AD平分∠BAC，则四边形AEDF是菱形【分析】由矩形的判定和菱形的判定即可得出结论．【解答】解：若AD⊥BC，则四边形AEDF是平行四边形，不一定是矩形；选项A错误；若AD垂直平分BC，则四边形AEDF是菱形，不一定是矩形；选项B错误；若BD＝CD，则四边形AEDF是平行四边形，不一定是菱形；选项C错误；若AD平分∠BAC，则四边形AEDF是菱形；正确；故选：D．【点评】本题考查了矩形的判定、菱形的判定；熟记菱形和矩形的判定方法是解决问题的关键．15．下列关于矩形的说法中正确的是（）A．对角线相等的四边形是矩形B．矩形的对角线相等且互相平分C．对角线互相平分的四边形是矩形D．矩形的对角线互相垂直且平分【分析】根据矩形的性质和判定定理逐个判断即可．【解答】解：A、对角线相等的平行四边形才是矩形，故本选项错误；B、矩形的对角线相等且互相平分，故本选项正确；C、对角线互相平分的四边形是平行四边形，不一定是矩形，故本选项错误；D、矩形的对角线互相平分且相等，不一定垂直，故本选项错误；故选：B．【点评】本题考查了矩形的性质和判定的应用，能熟记矩形的性质和判定定理是解此题的关键．16．如图，在矩形ABCD中，对角线AC，BD相交于点O，∠AOB＝60°，AC ＝6cm，则AB的长是（）A．3cm B．6cm C．10cm D．12cm【分析】根据矩形的对角线相等且互相平分可得OA＝OB＝OD＝OC，由∠AOB ＝60°，判断出△AOB是等边三角形，根据等边三角形的性质求出AB即可．【解答】解：∵四边形ABCD是矩形，∴OA＝OC＝OB＝OD＝3，∵∠AOB＝60°，∴△AOB是等边三角形，∴AB＝OA＝3，故选：A．【点评】本题考查了矩形的性质，等边三角形的判定与性质，熟记性质并判断出△AOB是等边三角形是解题的关键．17．如图，矩形ABCD的对角线AC与BD相交于点O，∠ADB＝30°，AB＝4，则OC＝（）A．5B．4C．3.5D．3【分析】由矩形的性质得出AC＝BD，OA＝OC，∠BAD＝90°，由直角三角形的性质得出AC＝BD＝2AB＝8，得出OC＝AC＝4即可．【解答】解：∵四边形ABCD是矩形，∴AC＝BD，OA＝OC，∠BAD＝90°，∵∠ADB＝30°，∴AC＝BD＝2AB＝8，∴OC＝AC＝4；故选：B．【点评】此题考查了矩形的性质、含30°角的直角三角形的性质．熟练掌握矩形的性质，注意掌握数形结合思想的应用．18．如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若AC＝4，则四边形OCED的周长为（）A．4B．8C．10D．12【分析】由四边形ABCD为矩形，得到对角线互相平分且相等，得到OD＝OC，再利用两对边平行的四边形为平行四边形得到四边形DECO为平行四边形，利用邻边相等的平行四边形为菱形得到四边形DECO为菱形，根据AC的长求出OC的长，即可确定出其周长．【解答】解：∵四边形ABCD为矩形，∴OA＝OC，OB＝OD，且AC＝BD，∴OA＝OB＝OC＝OD＝2，∵CE∥BD，DE∥AC，∴四边形DECO为平行四边形，∵OD＝OC，∴四边形DECO为菱形，∴OD＝DE＝EC＝OC＝2，则四边形OCED的周长为2+2+2+2＝8，故选：B．【点评】此题考查了矩形的性质，以及菱形的判定与性质，熟练掌握判定与性质是解本题的关键．19．如图，矩形ABCD的对角线AC与BD相交于点O，CE∥BD，DE∥AC，AD ＝2，DE＝2，则四边形OCED的面积为（）A．2B．4C．4D．8【分析】连接OE，与DC交于点F，由四边形ABCD为矩形得到对角线互相平分且相等，进而得到OD＝OC，再由两组对边分别平行的四边形为平行四边形得到ODEC为平行四边形，根据邻边相等的平行四边形为菱形得到四边形ODEC为菱形，得到对角线互相平分且垂直，求出菱形OCED的面积即可．【解答】解：连接OE，与DC交于点F，∵四边形ABCD为矩形，∴OA＝OC，OB＝OD，且AC＝BD，即OA＝OB＝OC＝OD，∵OD∥CE，OC∥DE，∴四边形ODEC为平行四边形，∵OD＝OC，∴四边形ODEC为菱形，∴DF＝CF，OF＝EF，DC⊥OE，∵DE∥OA，且DE＝OA，∴四边形ADEO为平行四边形，∵AD＝2，DE＝2，∴OE＝2，即OF＝EF＝，在Rt△DEF中，根据勾股定理得：DF＝＝1，即DC＝2，＝OE•DC＝×2×2＝2．则S菱形ODEC故选：A．【点评】此题考查了矩形的性质，菱形的判定与性质，以及勾股定理，熟练掌握矩形的性质是解本题的关键．20．矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），D是OA的中点，点E在AB上，当△CDE的周长最小时，点E的坐标为（）A．（3，1）B．（3，）C．（3，）D．（3，2）【分析】如图，作点D关于直线AB的对称点H，连接CH与AB的交点为E，此时△CDE的周长最小，先求出直线CH解析式，再求出直线CH与AB的交点即可解决问题．【解答】解：如图，作点D关于直线AB的对称点H，连接CH与AB的交点为E，此时△CDE的周长最小．∵D（，0），A（3，0），∴H（，0），∴直线CH解析式为y＝﹣x+4，∴x＝3时，y＝，∴点E坐标（3，）故选：B．【点评】本题考查矩形的性质、坐标与图形的性质、轴对称﹣最短问题、一次函数等知识，解题的关键是利用轴对称找到点E位置，学会利用一次函数解决交点问题，属于中考常考题型．21．如图，矩形ABCD中，AD＝2，AB＝3，过点A，C作相距为2的平行线段AE，CF，分别交CD，AB于点E，F，则DE的长是（）A．B．C．1D．【分析】过F作FH⊥AE于H，根据矩形的性质得到AB＝CD，AB∥CD，推出四边形AECF是平行四边形，根据平行四边形的性质得到AF＝CE，根据相似三角形的性质得到，于是得到AE＝AF，列方程即可得到结论．【解答】解：过F作FH⊥AE于H，∵四边形ABCD是矩形，∴AB＝CD，AB∥CD，∵AE∥CF，∴四边形AECF是平行四边形，∴AF＝CE，∴DE＝BF，∴AF＝3﹣DE，∴AE＝，∵∠FHA＝∠D＝∠DAF＝90°，∴∠AFH+∠HAF＝∠DAE+∠F AH＝90°，∴∠DAE＝∠AFH，∴△ADE∽△AFH，∴，∴AE＝AF，∴＝3﹣DE，∴DE＝，故选：D．解法二：∵四边形ABCD是矩形，∴AB∥CD，∴∠F AH＝∠AED，∵∠ADE＝∠AHF＝∠DAF＝90°，AD＝2，FH＝2，∴AD＝FH，∴△ADE≌△F AH，∴AF＝AE，∵AE∥CF，AF∥EC，∴四边形AECF是平行四边形，∵AF＝AE，∴四边形AECF是菱形，设DE＝x，则BF＝x，CE＝CF＝3﹣x，在Rt△BCF中，（3﹣x）2＝x2+22，∴x＝．故选：D．【点评】本题考查了矩形的性质，相似三角形的判定和性质，勾股定理，平行四边形的判定和性质，熟练掌握平行四边形的判定定理是解题的关键．二．填空题（共10小题）22．如图，矩形OABC的顶点A，C分别在坐标轴上，B（8，7），D（5，0），点P是边AB或边BC上的一点，连接OP，DP，当△ODP为等腰三角形时，点P的坐标为（8，4）或（，7）．【分析】分两种情形分别讨论即可解决问题；【解答】解：∵四边形OABC是矩形，B（8，7），∴OA＝BC＝8，OC＝AB＝7，∵D（5，0），∴OD＝5，∵点P是边AB或边BC上的一点，∴当点P在AB边时，OD＝DP＝5，∵AD＝3，∴P A＝＝4，∴P（8，4）．当点P在边BC上时，只有PO＝PD，此时P（，7）．综上所述，满足条件的点P坐标为（8，4）或（，7）．故答案为（8，4）或（，7）．【点评】本题考查矩形的性质、坐标与图形性质、等腰三角形的判定等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．23．如图，矩形EFGH的四个顶点分别在矩形ABCD的各条边上，AB＝EF，FG ＝2，GC＝3．有以下四个结论：①∠BGF＝∠CHG；②△BFG≌△DHE；③tan∠BFG＝；④矩形EFGH的面积是4．其中一定成立的是①②④．（把所有正确结论的序号填在横线上）【分析】根据矩形的性质和全等三角形的判定分析各小题即可；【解答】解：∵∠FGH＝90°，∴∠BGF+∠CGH＝90°．又∵∠CGH+∠CHG＝90°，∴∠BGF＝∠CHG，故①正确．同理可得∠DEH＝∠CHG．∴∠BGF＝∠DEH．又∵∠B＝∠D＝90°，FG＝EH，∴△BFG≌△DHE，故②正确．同理可得△AFE≌△CHG．∴AF＝CH．易得△BFG∽△CGH．设GH、EF为a，∴＝．∴＝．∴BF＝．∴AF＝AB﹣BF＝a﹣．∴CH＝AF＝a﹣．在Rt△CGH中，∵CG2+CH2＝GH2，∴32+（a﹣）2＝a2．解得a＝2．∴GH＝2．∴BF＝a﹣＝．在Rt△BFG中，∵cos∠BFG＝＝，∴∠BFG＝30°．∴tan∠BFG＝tan30°＝，故③错误．矩形EFGH的面积＝FG×GH＝2×2＝4，故④正确．故答案为：①②④【点评】此题是几何变换综合题，主要考查了全等三角形的判定和性质，矩形的判定和性质，属于基础题．24．如图，在矩形ABCD中，AB＝4，AD＝2，点E在CD上，DE＝1，点F是边AB上一动点，以EF为斜边作Rt△EFP．若点P在矩形ABCD的边上，且这样的直角三角形恰好有两个，则AF的值是0或1＜AF或4．【分析】先根据圆周角定理确定点P在以EF为直径的圆O上，且是与矩形ABCD 的交点，先确定特殊点时AF的长，当F与A和B重合时，都有两个直角三角形．符合条件，即AF＝0或4，再找⊙O与AD和BC相切时AF的长，此时⊙O与矩形边各有一个交点或三个交点，在之间运动过程中符合条件，确定AF的取值．【解答】解：∵△EFP是直角三角形，且点P在矩形ABCD的边上，∴P是以EF为直径的圆O与矩形ABCD的交点，①当AF＝0时，如图1，此时点P有两个，一个与D重合，一个交在边AB上；②当⊙O与AD相切时，设与AD边的切点为P，如图2，此时△EFP是直角三角形，点P只有一个，当⊙O与BC相切时，如图4，连接OP，此时构成三个直角三角形，则OP⊥BC，设AF＝x，则BF＝P1C＝4﹣x，EP1＝x﹣1，∵OP∥EC，OE＝OF，∴OG＝EP1＝，∴⊙O的半径为：OF＝OP＝，在Rt△OGF中，由勾股定理得：OF2＝OG2+GF2，∴，解得：x＝，∴当1＜AF＜时，这样的直角三角形恰好有两个，③当AF＝4，即F与B重合时，这样的直角三角形恰好有两个，如图5，综上所述，则AF的值是：0或1＜AF或4．故答案为：0或1＜AF或4．【点评】本题考查了矩形的性质的运用，勾股定理的运用，三角形中位线定理的运用，圆的性质的运用，分类讨论思想的运用，解答时运用勾股定理求解是关键，并注意运用数形结合的思想解决问题..25．对于一个位置确定的图形，如果它的所有点都在一个水平放置的矩形内部或边上，且该图形与矩形的每条边都至少有一个公共点（如图1），那么这个矩形水平方向的边长称为该图形的宽，铅锤方向的边长称为该矩形的高．如图2，菱形ABCD的边长为1，边AB水平放置．如果该菱形的高是宽的，那么它的宽的值是．【分析】先根据要求画图，设矩形的宽AF＝x，则CF＝x，根据勾股定理列方程可得结论．【解答】解：在菱形上建立如图所示的矩形EAFC，设AF＝x，则CF＝x，在Rt△CBF中，CB＝1，BF＝x﹣1，由勾股定理得：BC2＝BF2+CF2，，解得：x＝或0（舍），即它的宽的值是，故答案为：．【点评】本题考查了新定义、矩形和菱形的性质、勾股定理，理解新定义中矩形的宽和高是关键．26．如图，平面直角坐标系中，矩形OABC的顶点A（﹣6，0），C（0，2）．将矩形OABC绕点O顺时针方向旋转，使点A恰好落在OB上的点A1处，则点B的对应点B1的坐标为（﹣2，6）．【分析】连接OB1，作B1H⊥OA于H，证明△AOB≌△HB1O，得到B1H＝OA ＝6，OH＝AB＝2，得到答案．【解答】解：连接OB1，作B1H⊥OA于H，由题意得，OA＝6，AB＝OC＝2，则tan∠BOA＝＝，∴∠BOA＝30°，∴∠OBA＝60°，由旋转的性质可知，∠B1OB＝∠BOA＝30°，∴∴∠B1OH＝60°，在△AOB和△HB1O，，∴△AOB≌△HB1O，∴B1H＝OA＝6，OH＝AB＝2，∴点B1的坐标为（﹣2，6），故答案为：（﹣2，6）．【点评】本题考查的是矩形的性质、旋转变换的性质，掌握矩形的性质、全等三角形的判定和性质定理是解题的关键．27．如图，E、F，G、H分别为矩形ABCD的边AB、BC、CD、DA的中点，连接AC、HE、EC，GA，GF．已知AG⊥GF，AC＝，则AB的长为2．【分析】如图，连接BD．由△ADG∽△GCF，设CF＝BF＝a，CG＝DG＝b，可得＝，推出＝，可得b＝a，在Rt△GCF中，利用勾股定理求出b，即可解决问题；【解答】解：如图，连接BD．∵四边形ABCD是矩形，∴∠ADC＝∠DCB＝90°，AC＝BD＝，∵CG＝DG，CF＝FB，∴GF＝BD＝，∵AG⊥FG，∴∠AGF＝90°，∴∠DAG+∠AGD＝90°，∠AGD+∠CGF＝90°，∴∠DAG＝∠CGF，∴△ADG∽△GCF，设CF＝BF＝a，CG＝DG＝b，∴＝，∴＝，∴b2＝2a2，∵a＞0．b＞0，∴b＝a，在Rt△GCF中，3a2＝，∴a＝，∴AB＝2b＝2．故答案为2．【点评】本题考查三角形中位线定理、矩形的性质、相似三角形的判定和性质、勾股定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．28．如图，矩形ABCD的对角线AC与BD相交点O，AC＝10，P、Q分别为AO、AD的中点，则PQ的长度为 2.5．【分析】根据矩形的性质可得AC＝BD＝10，BO＝DO＝BD＝5，再根据三角形中位线定理可得PQ＝DO＝2.5．【解答】解：∵四边形ABCD是矩形，∴AC＝BD＝10，BO＝DO＝BD，∴OD＝BD＝5，∵点P、Q是AO，AD的中点，∴PQ是△AOD的中位线，∴PQ＝DO＝2.5．故答案为：2.5．【点评】此题主要考查了矩形的性质，以及三角形中位线定理，关键是掌握矩形对角线相等且互相平分．29．如图，在平行四边形ABCD中，添加一个条件AC＝BD或∠ABC＝90°，使平行四边形ABCD是矩形．。

矩形课后练习1、矩形具有而平行四边形不具有的性质是()A．内角和为360°B．对角线相等C．对角相等D．相邻两角互补2、平行四边形、矩形、菱形、正方形都具有的性质()A．对角线相等B．对角线互相平分C．对角线平分一组对角D．对角线互相垂直3、下列关于矩形的说法中正确的是()A．矩形的对角线互相垂直且平分B．矩形的对角线相等且互相平分C．对角线相等的四边形是矩形D．对角线互相平分的四边形是矩形下列说法正确的有()①两条对角线相等的四边形是矩形；②有一组对边相等，一组对角是直角的四边形是矩形；③一个角为直角，两条对角线相等的四边形是矩形；④四个角都相等的四边形是矩形；⑤对角线相等且垂直的四边形是矩形；⑥有一个角是直角的平行四边形是矩形．A．1个B．2个C．3个D．4个4、如图，在矩形ABCD中，AE⊥BD，垂足为E，∠DAE：∠BAE=1：2，试求∠CAE的度数．5、如图，已知矩形ABCD中，AC与BD相交于O，DE平分∠ADC交BC于E，∠BDE=15°，试求∠COE的度数．6、Rt△ABC中，∠BAC=90°，AB=3，AC=4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM 的最小值为．7、如图，在Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2，E是AB边的中点，F是AC边的中点，D是BC边上一动点，则△EFD的周长最小值是．8、如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．9、(1)线段BD与CD有什么数量关系，并说明理由；(2)当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．10、如图，以△ABC的各边向同侧作正△ABD，正△BCF，正△ACE．(1)求证：四边形AEFD是平行四边形；(2)当∠BAC=______时，四边形AEFD是矩形；(3)当∠BAC=______时，以A、E、F、D为顶点的四边形不存在．11、如图，已知平行四边形ABCD，延长AD到E，使DE=AD，连接BE与DC交于O点．(1)求证：△BOC≌△EOD；(2)当∠A=12∠EOC时，连接BD、CE，求证：四边形BCED为矩形．12、已知四边形ABCD中，AB=CD，BC=DA，对角线AC、BD交于点O．M是四边形ABCD外的一点，AM⊥MC，BM⊥MD．试问：四边形ABCD是什么四边形，并证明你的结论．13、如图，△ABC中，AB=AC，D是BC中点，F是AC中点，AN是△ABC的外角∠MAC的角平分线，延长DF交AN于点E．(1)判断四边形ABDE的形状，并说明理由；(2)问：线段CE与线段AD有什么关系？请说明你的理由．14、已知：如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G．(1)求证：△ADE≌△CBF；(2)若四边形BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论．15、如图，矩形纸片ABCD的宽AD=5，现将矩形纸片ABCD沿QG折叠，使点C落到点R的位置，点P是QG上的一点，PE⊥QR于E，PF⊥AB于F，求PE+PF．16、如图，已知，E是矩形ABCD边AD上一点，且BE=ED，P是对角线BD上任一点，PF⊥BE，PG⊥AD，垂足分别为F、G，你知道PF+PG与AB有什么关系吗？并证明你的结论．矩形课后练习参考答案题一： B ．详解：A ．内角和为360°矩形与平行四边形都具有，故此选项错误；B ．对角线相等只有矩形具有，而平行四边形不具有，故此选项正确；C ．对角相等矩形与平行四边形都具有，故此选项错误；D ．相邻两角互补矩形与平行四边形都具有，故此选项错误．故选B ． 题二： B ．详解：因为平行四边形的对角线互相平分、正方形的对角线垂直平分且相等、矩形的对角线互相平分且相等、菱形的对角线互相垂直平分，可知正方形、矩形、菱形都具有的特征是对角线互相平分．故选B ．题三： B ．详解：A ．矩形的对角线互相平分，且相等，但不一定互相垂直，本选项错误；B ．矩形的对角线相等且互相平分，本选项正确；C ．对角线相等的四边形不一定为矩形，例如等腰梯形对角线相等，但不是矩形，本选项错误；D ．对角线互相平分的四边形为平行四边形，不一定为矩形，本选项错误．故选B ．题四： C ．详解：两条对角线相等且相互平分的四边形为矩形，故①③⑤错；有一个角为直角的平行四边形为矩形，故②④⑥正确．故选C ． 题五： 30°．详解：∵∠DAE ：∠BAE =1：2，∠DAB =90°，∴∠DAE =30°，∠BAE =60°，∴∠DBA =90°-∠BAE =90°-60°=30°，∵OA =OB ，∴∠OAB =∠OBA =30°，∴∠CAE =∠BAE -∠OAB =60°-30°=30°．题六： 75°．详解：∵四边形ABCD 是矩形，DE 平分∠ADC ，∴∠CDE =∠CED = 45°，∴EC =DC ，又∵∠BDE =15°，∴∠CDO =60°，又∵矩形的对角线互相平分且相等，∴OD =OC ，∴△OCD 是等边三角形，∴∠DCO =60°，∠OCB =90°-∠DCO =30°，∵DE 平分∠ADC ，∠ECD =90°，∠CDE =∠CED = 45°，∴CD =CE =CO ，∴∠COE =∠CEO ；∴∠COE =(180°-30°)÷2=75°．题七： 65．详解：由题意知，四边形AFPE 是矩形，∵点M 是矩形对角线EF 的中点，则延长AM 应过点P ，∴当AP 为Rt △ABC 的斜边上的高时，即AP ⊥BC 时，AM 有最小值，此时AM =12AP ，由勾股定理知BC =22AB AC +=5，∵S △ABC =12AB •AC =12BC •AP ，∴AP =345⨯=125，∴AM =12AP =65． 题八： 1+13．详解：作点F 关于BC 的对称点G ，连接EG ，交BC 于D 点，D 点即为所求，∵E 是AB 边的中点，F 是AC 边的中点，∴EF 为△ABC 的中位线，∵BC =2，∴EF =12BC =12×2=1；∵EF 为△ABC 的中位线，∴EF ∥BC ，∴∠EFG =∠C =90°，又∵∠ABC =60°，BC =2，FG =AC =23，EG =22EF FG +=13，∴DE +FE +DF =EG +EF =1+13．题九： 见详解．详解：(1)BD =CD ．理由：∵AF ∥BC ，∴∠AFE =∠DCE ，∵E 是AD 的中点， ∴AE =DE ，在△AEF 和△DEC 中，∠AFE =∠DCE ，∠AEF =∠DEC ，AE =DE ，∴△AEF ≌△DEC (AAS)，∴AF =CD ，∵AF =BD ，∴BD =CD ；(2)当△ABC 满足：AB =AC 时，四边形AFBD 是矩形．理由：∵AF ∥BD ，AF =BD ，∴四边形AFBD 是平行四边形，∵AB =AC ，BD =CD ，∴∠ADB =90°，∴平行四边形AFBD 是矩形． 题十： 见详解．详解：(1)∵△BCF 和△ACE 是等边三角形，∴AC =CE ，BC =CF ，∠ECA =∠BCF =60°，∴∠ECA -∠FCA =∠BCF -∠FCA ，即∠ACB =∠ECF ，∵在△ACB 和△ECF 中，AC =CE ，∠ACB =∠ECF ，BC =CF ，∴△ACB ≌△ECF (SAS)，∴EF =AB ，∵三角形ABD 是等边三角形，∴AB =AD ，∴EF =AD =AB ，同理FD =AE =AC ，即EF =AD ，DF =AE ，∴四边形AEFD 是平行四边形；(2)当∠BAC =150°时，平行四边形AEFD 是矩形，理由：∵△ADB 和△ACE 是等边三角形，∴∠DAB =∠EAC =60°，∵∠BAC =150°，∴∠DAE =360°-60°-60°-150°=90°，∵由(1)知：四边形AEFD 是平行四边形，∴平行四边形AEFD 是矩形．(3)当∠BAC =60°时，以A 、E 、F 、D 为顶点的四边形不存在，理由如下：∵∠DAB =∠EAC =60°，∠BAC =60°，∴∠DAE =60°+60°+60°=180°，∴D 、A 、E 三点共线，即边DA 、AE 在一条直线上，∴当∠BAC =60°时，以A 、E 、F 、D 为顶点的四边形不存在．题十一： 见详解．详解：(1)∵在平行四边形ABCD 中，AD =BC ，AD ∥BC ，∴∠EDO =∠BCO ，∠DEO =∠CBO ，∵DE =AD ，∴DE =BC ， 在△BOC 和△EOD 中，∠OBC =∠OED ，BC =DE ，∠OCB =∠ODE ，∴△BOC ≌△EOD (ASA)；(2)∵DE =BC ，DE ∥BC ，∴四边形BCED 是平行四边形， 在平行四边形ABCD 中，AB ∥DC ，∴∠A =∠ODE ，∵∠A =12∠EOC ，∴∠ODE =12∠EOC ， ∵∠ODE +∠OED =∠EOC ，∴∠ODE =∠OED ，∴OE =OD ，∵平行四边形BCED 中，CD =2OD ，B E =2OE ，∴CD =BE ，∴平行四边形BCED 为矩形．题十二：见详解．详解：矩形．理由：连接OM，∵AB=CD，BC=DA，∴四边形ABCD是平行四边形，∴OA=OC，OB=OD，∵AM⊥MC，BM⊥MD，∴∠AMC=∠BMD=90°，∴OM=12BD，OM=12AC，∴BD=AC，∴四边形ABCD是矩形．题十三：见详解．详解：(1)四边形ABDE是平行四边形，理由：∵AB=AC，D是BC中点，F是AC中点，∴DF∥AB，∵AB=AC，D是BC 中点，∴∠BAD=∠CAD，AD⊥DC，∵AN是△ABC的外角∠MAC的角平分线，∴∠MAE=∠CAE，∴∠NAD=90°，∴AE∥BD，∴四边形ABDE是平行四边形；(2)CE∥AD，CE=AD；理由：∵AN是△ABC外角∠CAM的平分线，∴∠MAE=12∠MAC，∵∠MAC=∠B+∠ACB，∵AB=AC，∴∠B=∠ACB，∴∠MAE=∠B，∴AN∥BC，∵AB=AC，点D为BC中点，∴AD⊥BC，∵CE⊥AN，∴AD∥CE，∴四边形ADCE为平行四边形，∵CE⊥AN，∴∠AEC=90°，∴四边形ADCE为矩形，∴CE∥AD，CE=AD．题十四：见详解．详解：(1)∵四边形ABCD是平行四边形，∴∠4=∠C，AD=CB，AB=CD，∵点E、F分别是AB、CD的中点，∴AE=12 AB，CF=12CD．∴AE=CF，在△AED与△CBF中，AD=CB，∠4=∠C，AE=CF，∴△ADE≌△CBF(SAS)，(2)当四边形BEDF是菱形时，四边形AGBD是矩形；证明：∵四边形ABCD是平行四边形，∴AD∥BC，∵AG∥BD，∴四边形AGBD是平行四边形，∵四边形BEDF是菱形，∴DE=BE，∵AE=BE，∴AE=BE=DE，∴∠1=∠2，∠3=∠4，∵∠1+∠2+∠3+∠4=180°，∴2∠2+2∠3=180°，∴∠2+∠3=90°，即∠ADB=90°，∴四边形AGBD是矩形．题十五：5．详解：把折叠的图展开，如图所示：EF=AD，∵AD=5，∴EF=5，∴PF+PE=5．题十六：PF+PG =AB．详解：PF+PG=AB．理由如下：连接PE，则S△BEP+S△DEP=S△BED，即12BE•PF+12DE•PG =12DE•AB．又∵BE=DE，∴12DE•PF+12DE•PG=12DE•AB，即12DE(PF+PG)=12DE•AB，∴PF+PG =AB．。

第5章特殊平行四边形5.1矩形(1)A练就好基础基础达标1．矩形具有而一般平行四边形不具有的性质是(A)A．对角线相等B．对角相等C．对边相等D．对角线互相平分224cm，则这个矩形的一条较短边为(C)A．12cm B．8cm C．6cm D．5cm3．若矩形的对角线长为4cm，一条边长为2cm，则此矩形的面积为(B)A．83cm2B．43cm2C．23cm2D．8cm24．如图所示，在矩形ABCD中，对角线AC，BD交于点O，下列说法错误的是(C)A．AB∥DC B．AC＝BDC．AC⊥BD D．OA＝OC题图第5题图5．如图所示，EF过矩形ABCD对角线的交点O，且分别交AD，BC于点E，F.已知AB＝3，BC＝4，则图中阴影部分的面积是(A)A．3B．4C．6D．126．如图所示，在矩形ABCD中，对角线O，点E，F分别是AO，AD的中点，若AB＝6cm，BC＝8cm，则EF的长是__2.5__cm.7．如图所示，在矩形ABCD中，CE⊥BD，点E为垂足，连结AE.若∠DCE∶∠ECB＝3∶1，则∠ACE ＝__45°__.第8题图8．如图所示，将四根木条钉成的长方形木框变形为平行四边形ABC′D′的形状，并使其面积为长方形面积的22(木条宽度忽略不计)，则这个平行四边形的最小内角为__45__度．解：过点C′作AB的垂线，垂足是点E∵将四根木条钉成的矩形木框变形为平行四边形木框ABC′D′的形状，并使其面积为矩形木框的2 2，∴C′E＝22BC＝22BC′，∴BC′＝2C′E，∴∠C′BE＝∠D′AB＝45°.9．如图所示，已知矩形ABCD的对角线AC与BD交于点O.(1)求证：∠ACD＝∠ABD.(2)若矩形ABCD的面积为120cm2解：(1)证明：在矩形ABCD中，易得∠OC＝OB，∴∠OBC＝∠OCB.∴∠DCB－∠OCB＝∠ABC－∠OBC，∴∠ACD＝∠ABD.(2)在Rt△ABC中，AC＝AB2＋BC2＝17.10．如图所示，BD为矩形ABCD的一条对角线，延长BC至点E，使CE＝BD，连结AE，若AB＝1，∠AEB＝15°，求AD解：如图，连结AC，∵四边形ABCD是矩形，∴AD∥BE，AC＝BD，且∠ADB＝∠CAD，∴∠E＝∠DAE.又∵BD＝CE，∴CE＝CA，∴∠E＝∠CAE.∵∠CAD＝∠CAE＋∠DAE＝30°，∴∠ADB＝30°，∴BD＝2AB＝2，∴AD＝BD2－AB2＝ 3.B更上一层楼能力提升11．如图所示，四边形ABCD和四边形AEFC是两个矩形，点B在EF边上，若矩形ABCD和矩形AEFC的面积分别是S1，S2，则S1，S2)A．S1＝S2B．S1＞S2C．S1＜S2D．3S1＝2S212．如图所示，△ABC是以AB为斜边的直角三角形，AC＝4，BC＝3，P为AB上一动点，且PE⊥AC 于点E，PF⊥BC于点F，则线段EF长度的最小值是__2.4__．题图13题图13．如图所示，在矩形ABCD 中，AC ，BD 相交于点O ，AE 平分∠BAD 交BC 于点E .若∠CAE ＝15°，则∠BOE 的度数是__75°__．14．2018·威海矩形ABCD 与CEFG ，如图放置，点B ，C ，E 共线，点C ，D ，G 共线，连结AF ，取AF 的中点H ，连结CE 解：如图，延长GH 交AD 于点P ，∵四边形ABCD 和四边形CEFG 都是矩形，∴∠ADC ＝∠ADG ＝∠CGF ＝90°，AD ＝BC ＝2，GF ＝CE ＝1，∴AD ∥GF ，∴∠GFH ＝∠PAH .又∵H 是AF 的中点，∴AH ＝FH .在△APH 和△FGH 中，∠PAH ＝∠GFH ，AH ＝FH ，∠AHP ＝∠FHG ，∴△APH ≌△FGH (ASA )，∴AP ＝GF ＝1，GH ＝PH ＝12PG ，∴PD ＝AD －AP ＝1.∵CG ＝2，CD ＝1，∴DG ＝1，∴GH ＝12PG ＝12×PD 2＋DG 2＝22.15．如图所示，在矩形ABCD 中，E ，F 分别是边BC ，AB 上的点，且EF ＝ED ，EF ⊥ED .求证：AE 平分∠BAD .证明：∵四边形ABCD 是矩形，∴∠B ＝∠C ＝∠BAD ＝90°，AB ＝CD,∴∠BEF ＋∠BFE ＝90°.∵EF ⊥ED ，∴∠BEF ＋∠CED ＝90°.∴∠BFE ＝∠CED .又∵EF ＝ED ，∴△EBF ≌△DCE (AAS )．∴BE＝CD.∴BE＝AB，∴∠BAE＝∠BEA＝45°.∴∠EAD＝45°.∴∠BAE＝∠EAD.∴AE平分∠BAD.C开拓新思路拓展创新16．如图所示，四边形ABCD是矩形，P是矩形外一点，且PA＝PB.(1)求证：PD＝PC.(2)若△PAB的面积为S1，△PCD2的面积为________．解：(1)证明：∵四边形ABCD是矩形，∴AD＝BC，∠DAB＝∠ABC＝90°.∵PA＝PB，∴∠PAB＝∠PBA，∴∠PAD＝∠PBC.在△APD和△BPC PA＝PB，∠PAD＝∠PBC，AD＝BC，∴△APD≌△BPC(SAS)，∴PD＝PC.(2)2(S1－S2)。

5．1 矩形矩形的性质1．如图，将矩形ABCD沿对角线BD折叠，使点C和点C′重合,若AB＝2，则C′D的长为( )A．1 B．2 C．3 D．42．在矩形ABCD中，点O是BC的中点，∠AOD＝90°，矩形ABCD的周长为30 cm，则AB的长为（）A．3 cm B．4 cm C．5 cm D．6 cm3．如图,矩形ABCD中,AB＝2，BC＝4，点A，B分别在y轴、x轴的正半轴上，点C在第一象限,如果∠OAB＝30°,那么点C的坐标是__________________________．4．如图,在矩形ABCD中，E，F为BC上两点，且BE＝CF，连结AF,DE交于点O。

求证：（1）△ABF≌△DCE；（2）△AOD是等腰三角形．5．如图，在矩形ABCD中，对角线AC，BD交于点O，以下说法错误的是( ）A．∠ABC＝90° B．AC＝BD C．OA＝OB D．OA＝AD6．如图，矩形ABCD的两条对角线相交于点O，∠AOD＝60°，AD＝2，则AC的长是( )A．2 B．4 C．2 3 D．437．如图，矩形OBCD的顶点C的坐标为（1，3），则对角线BD的长等于( )A。

错误! B．2错误! C．2错误! D.错误!8．如图，矩形ABCD的两条对角线交于点O，过点O作AC的垂线EF，分别交AD，BC于点E，F,连结CE，已知△CDE的周长为24 cm,则矩形ABCD的周长是____cm。

9．如图,在平面直角坐标系中，矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°，OC＝2，则点B的坐标是__________10．如图，四边形ABCD是矩形，对角线AC，BD相交于点O，BE∥AC交DC的延长线于点E.(1)求证：BD＝BE；(2）若∠DBC＝30°，BO＝4,求四边形ABED的面积．11．如图，四边形ABCD和四边形AEFC是两个矩形，点B在边EF上，若矩形ABCD和矩形AEFC的面积分别是S1，S2，则S1，S2的大小关系是（ )A．S1＞S2 B．S1＝S2 C．S1＜S2 D．3S1＝2S212．如图,在矩形ABCD中，AB＝8，BC＝4，将矩形沿AC折叠，则重叠部分△AFC的面积为（ )A．12 B．10 C．8 D．613．如图，在矩形ABCD中，DE⊥AC于点E，∠EDC∶∠EDA＝1∶3，且AC＝10，则DE的长度是（）A．3 B．5 C．5错误! D.错误!14．如图，矩形ABCD中，AB＝3，BC＝4,则图中五个小矩形的周长之和为____．15．如图，矩形ABCD中，AB＝3 cm,BC＝4 cm，E是边AD上一点，且BE＝ED,P是对角线上任意一点，PF⊥BE，PG⊥AD，垂足分别为F，G.则PF＋PG的长为____cm.16．如图，在矩形ABCD中,E，F分别是边BC,AB上的点，且EF＝ED，EF⊥ED.求证:AE平分∠BAD.17．在矩形ABCD中，点E是BC上一点,AE＝AD，DF⊥AE，垂足为F.求证:DF＝DC。

正方形（03）一、选择题1．小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使▱ABCD为正方形（如图），现有下列四种选法，你认为其中错误的是（）A．①② B．②③ C．①③ D．②④2．下列命题中，真命题是（）A．对角线相等的四边形是矩形B．对角线互相垂直的四边形是菱形C．对角线互相平分的四边形是平行四边形D．对角线互相垂直平分的四边形是正方形3．顺次连接菱形各边的中点所形成的四边形是（）A．等腰梯形 B．矩形 C．菱形 D．正方形4．如图，在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE=BF，添加一个条件，仍不能证明四边形BECF为正方形的是（）A．BC=AC B．CF⊥BF C．BD=DF D．AC=BF5．下列说法中，正确的是（）A．相等的角一定是对顶角B．四个角都相等的四边形一定是正方形C．平行四边形的对角线互相平分D．矩形的对角线一定垂直6．如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF，②∠DAF=15°，③AC垂直平分EF，④BE+DF=EF，⑤S△CEF=2S△ABE．其中正确结论有（）个．A．4 B．3 C．2 D．17．已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是（）A．选①②B．选②③C．选①③D．选②④8．如图，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为F，则EF的长为（）A．1 B． C．4﹣2 D．3﹣4二、填空题9．如图，菱形ABCD中，对角线AC、BD相交于点O，不添加任何辅助线，请添加一个条件，使四边形ABCD是正方形（填一个即可）．10．如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上，下列结论：①CE=CF；②∠AEB=75°；③BE+DF=EF；④S正方形ABCD=2+．其中正确的序号是（把你认为正确的都填上）．11．如图，正方形ABCD的边长为2，过点A作AE⊥AC，AE=1，连接BE，则tanE= ．12．如图，正方形ABCD的边长为3，点E，F分别在边AB、BC上，AE=BF=1，小球P从点E出发沿直线向点F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当小球P第一次碰到点E时，小球P所经过的路程为．13．如图，已知线段AB=10，AC=BD=2，点P是CD上一动点，分别以AP、PB为边向上、向下作正方形APEF和PHKB，设正方形对角线的交点分别为O1、O2，当点P从点C运动到点D时，线段O1O2中点G的运动路径的长是．14．如图，E，F是正方形ABCD的边AD上两个动点，满足AE=DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是．15．如图，正方形ABCD的边长为4，点E在BC上，四边形EFGB也是正方形，以B为圆心，BA长为半径画，连结AF，CF，则图中阴影部分面积为．16．如图，正方形ABCD的边长为3，点E，F分别在边AB，BC上，AE=BF=1，小球P从点E出发沿直线向点F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当小球P第一次碰到点E时，小球P与正方形的边碰撞的次数为，小球P所经过的路程为．三、解答题17．如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC，P是B D上一点，过点P作PM⊥AD，PN ⊥CD，垂足分别为M，N．（1）求证：∠ADB=∠CDB；（2）若∠ADC=90°，求证：四边形MPND是正方形．18．如图，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．（1）求证：CE=AD；（2）当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由；（3）若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．19．如图，过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E．（1）判断四边形ACED的形状，并说明理由；（2）若BD=8cm，求线段BE的长．。