戴维南定理的解析与练习
- 格式:doc
- 大小:440.01 KB
- 文档页数:7

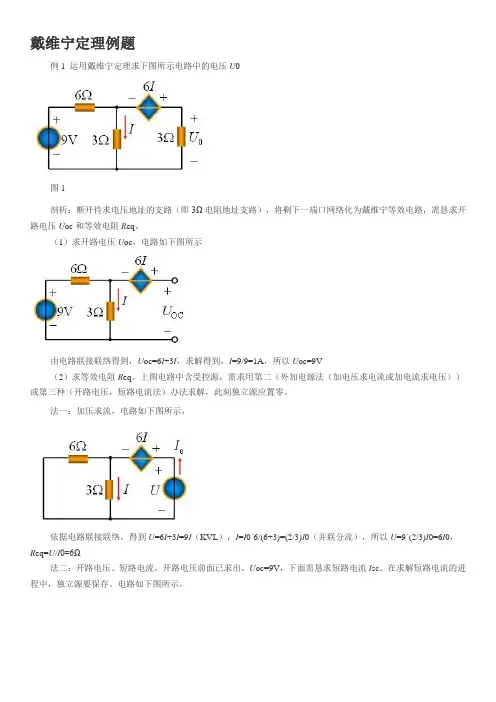
戴维宁定理例题例1 运用戴维宁定理求下图所示电路中的电压U0图1剖析:断开待求电压地址的支路(即3Ω电阻地址支路),将剩下一端口网络化为戴维宁等效电路,需恳求开路电压U oc和等效电阻R eq。
(1)求开路电压U oc,电路如下图所示由电路联接联络得到,U oc=6I+3I,求解得到,I=9/9=1A,所以U oc=9V(2)求等效电阻R eq。
上图电路中含受控源,需求用第二(外加电源法(加电压求电流或加电流求电压))或第三种(开路电压,短路电流法)办法求解,此刻独立源应置零。
法一:加压求流,电路如下图所示,依据电路联接联络,得到U=6I+3I=9I(KVL),I=I0´6/(6+3)=(2/3)I0(并联分流),所以U=9´(2/3)I0=6I0,R eq=U/I0=6Ω法二:开路电压、短路电流。
开路电压前面已求出,U oc=9V,下面需恳求短路电流I sc。
在求解短路电流的进程中,独立源要保存。
电路如下图所示。
依据电路联接联络,得到6I1+3I=9(KVL),6I+3I=0(KVL),故I=0,得到I sc=I1=9/6=1.5A(KCL),所以R eq=U oc/I sc=6Ω终究,等效电路如下图所示依据电路联接,得到留心:核算含受控源电路的等效电阻是用外加电源法仍是开路、短路法,要详细疑问详细剖析,以核算简练为好。
戴维南定理典型例子戴维南定理指出,等效二端网络的电动势E等于二端网络开路时的电压,它的串联内阻抗等于网络内部各独立源和电容电压、电感电流都为零时,从这二端看向网络的阻抗Zi。
设二端网络N中含有独立电源和线性时不变二端元件(电阻器、电感器、电容器),这些元件之间可以有耦合,即可以有受控源及互感耦合;网络N的两端ɑ、b接有负载阻抗Z(s),但负载与网络N内部诸元件之间没有耦合,U(s)=I(s)/Z(s)。
当网络N中所有独立电源都不工作(例如将独立电压源用短路代替,独立电流源用开路代替),所有电容电压和电感电流的初始值都为零的时候,可把这二端网络记作N0。

戴维南定理例题 -回复戴维南定理是一个在数学中常见的定理,它有许多不同的应用和例题。
我将从不同的角度给出一些例题来帮助你更好地理解这个定理。
例题1,在直角三角形ABC中,角A的对边长为3,角B的对边长为4。
求角C的对边长。
解:根据戴维南定理,我们可以利用公式a/sinA = b/sinB = c/sinC来求解。
首先,我们可以利用已知的信息计算出sinA和sinB的值,然后代入公式中进行求解。
计算过程如下:sinA = 对边长/斜边长 = 3/5。
sinB = 对边长/斜边长 = 4/5。
然后我们可以利用sinC = c/sinB来求解角C的对边长c:sinC = c/sinB.sinC = c/(4/5)。
c = 4sinC/5。
由此我们可以得出角C的对边长为4sinC/5。
例题2,在三角形ABC中,已知角A的度数为30°,角B的度数为60°,且边a的长度为5。
求边b和边c的长度。
解:根据戴维南定理,我们可以利用公式a/sinA = b/sinB = c/sinC来求解。
首先,我们可以利用已知的信息计算出sinA和sinB的值,然后代入公式中进行求解。
计算过程如下:sinA = sin30° = 1/2。
sinB = sin60° = √3/2。
然后我们可以利用a/sinA = b/sinB来求解边b的长度:5/1/2 = b/√3/2。
b = 5√3/2。
同样的方法,我们可以利用a/sinA = c/sinC来求解边c的长度:5/1/2 = c/sinC.c = 5/sinC.由此我们可以得出边b的长度为5√3/2,边c的长度为10/√3。
这些例题展示了戴维南定理在不同情况下的应用,希望能帮助你更好地理解和掌握这个定理。

复杂直流电路戴维宁定理专题1.利用戴维南定理求解如题83图中的电流I。
(1)断开待求支路,则开路电压U O=V;(5分)(2)等效电阻R O=Ω;(4分)(3)电流I= A。
(3分)题83图83.如图如示,试求:(1)用电源模型的等效变换求ab支路电流I;(6分,要有解题过程)(2)电压源端电压U;(3分)(3)3A恒流源的功率(2分),判断它是电源还是负载(1分)。
第83题图84.(12分)如题84图所示,试分析计算:(1)断开R,利用戴维南定理求有源二端网络的等效电压源模型。
(6分)(2)若a、b两端接上负载R,则R可获得最大功率是多少?(3分)(3)若负载R两端并接一个4μF的电容C,则C储存的电场能量是多少?(3分)第84题图解:(1)利用戴维南定理求解过程:第一步,开路电压U ab=_____V。
第二步,将题84图电路除源,画出无源二端网络如下:则无源二端网络的等效电阻R ab=____Ω.第三步,画出题84图的等效电路如下:(2)负载R L可获得最大功率的计算如下:(3)电容C储存的电场能量的计算如下:84.有源二端网络如图(a)所示,试分析计算:(1)利用戴维南定理求其等效电压源。
(8分)(2)若a、b两端接如图(b)所示电路图,则R L可获得的最大功率是多少?(4分)解:(1)利用戴维南定理求解过程:第一步,开路电压U ab=_____V。
(3分)第二步,将图(a)电路除源,画出无源二端网络如下:(2分)则无源二端网络的等效电阻R ab=____Ω.(1分)第三步,画出图(a)的等效电路如下:(2分)(2)如图(b)所示,负载R L可获得最大功率的计算如下:(4分)84、如题84(a)图所示电路中,用戴维宁定理求6Ω电阻中的电流I的大小,并计算30V 电压源的功率Pus,并说明是吸收功率还是产生功率。
解:第一步:将待求之路和3A电流源一起移开后如题84(b)图所示,求有源线性二端网络的开路电压U ab= V。

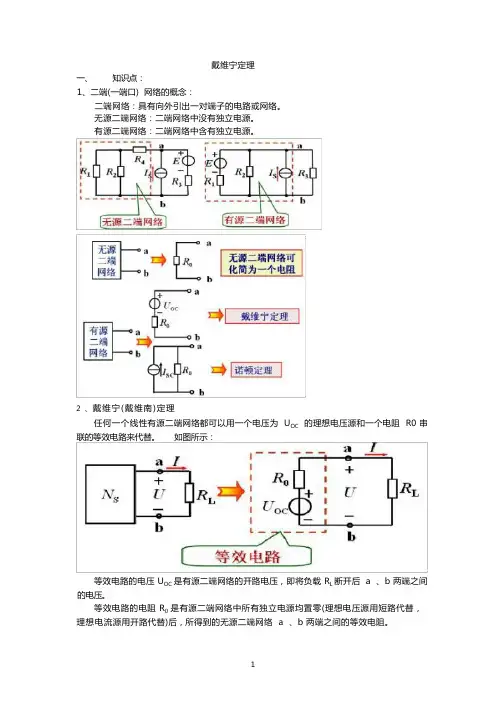
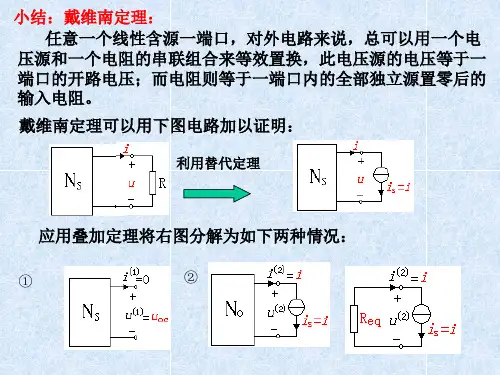
戴维宁定理一、知识点:1、二端(一端口) 网络的概念:二端网络:具有向外引出一对端子的电路或网络。
无源二端网络:二端网络中没有独立电源。
有源二端网络:二端网络中含有独立电源。
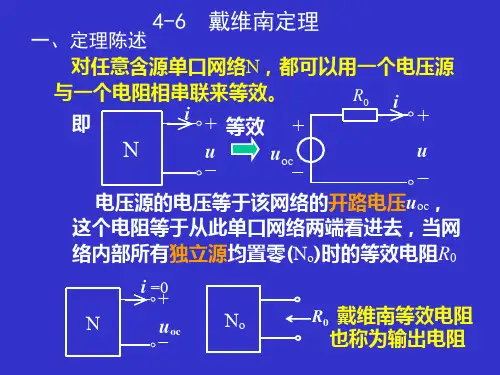
2、戴维宁(戴维南)定理任何一个线性有源二端网络都可以用一个电压为 U OC 的理想电压源和一个电阻 R0 串联的等效电路来代替。
如图所示:等效电路的电压 U OC 是有源二端网络的开路电压,即将负载 R L 断开后 a 、b 两端之间的电压。
等效电路的电阻 R0 是有源二端网络中所有独立电源均置零(理想电压源用短路代替,理想电流源用开路代替)后 , 所得到的无源二端网络 a 、b 两端之间的等效电阻。
二、例题:应用戴维南定理解题:戴维南定理的解题步骤:1.把电路划分为待求支路和有源二端网络两部分,如图 1 中的虚线。
2.断开待求支路,形成有源二端网络(要画图) ,求有源二端网络的开路电压 UOC 。
3.将有源二端网络内的电源置零,保留其内阻(要画图) ,求网络的入端等效电阻 Rab。
4.画出有源二端网络的等效电压源,其电压源电压 US=UOC (此时要注意电源的极性),内阻 R0=Rab 。
5.将待求支路接到等效电压源上,利用欧姆定律求电流。
例 1:电路如图,已知 U1=40V, U2=20V, R1=R2=4, R3=13 ,试用戴维宁定理求电流I3。
解: (1) 断开待求支路求开路电压UOCU U 40 20I = 1 2 = = 2.5 AR + R 4 +41 2UOC = U2 + I R2 = 20 +2.5 4 =30V或: UOC = U1 – I R1 = 40 –2.5 4 = 30VUOC 也可用叠加原理等其它方法求。
(2) 求等效电阻 R0将所有独立电源置零(理想电压源用短路代替,理想电流源用开路代替)R RR = 1 2 = 20 R + R1 2(3) 画出等效电路求电流 I3U OC 30I = = = 2 A3 R + R 2 +130 3例 2:试求电流 I1解: (1) 断开待求支路求开路电压 UOCUOC = 10 – 3 1 = 7V(2) 求等效电阻 R0R0 =3(3) 画出等效电路求电流 I3 a327V _ b 解得: I1 = 1. 4 A【例 3】 用戴维南定理计算图中的支路电流 I 3。

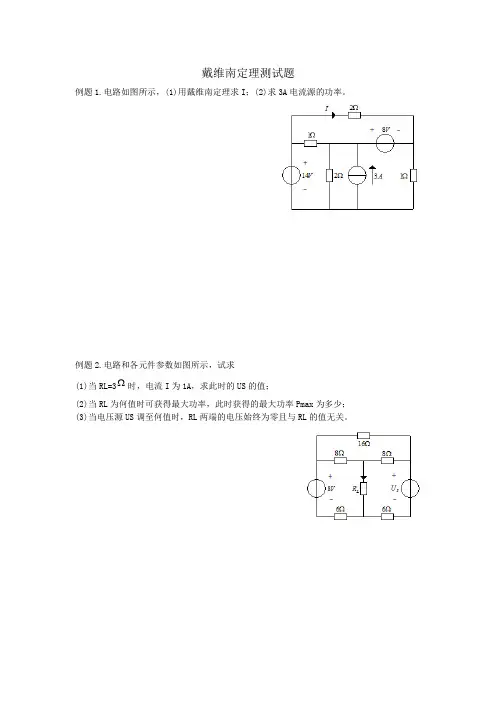
戴维南定理测试题
例题1.电路如图所示,(1)用戴维南定理求I;(2)求3A电流源的功率。
例题2.电路和各元件参数如图所示,试求
(1)当RL=3时,电流I为1A,求此时的US的值;
(2)当RL为何值时可获得最大功率,此时获得的最大功率Pmax为多少;
(3)当电压源US调至何值时,RL两端的电压始终为零且与RL的值无关。
例题3.如图所示电路中,当开关打在2位置时,电流表读数为2A,当开关打在1位置时,电流表读数为1A,试求:
(1)ab虚线左侧部分电路的等效电源参数;
(2)电流源IS2的电流为多少?
(3)要使开光打在1位置时,电流表读数为0,电流源IS2的电流为多少?
例题4.电路如图所示,(1)用戴维南定理求电流I1;(2)计算电阻R4消耗的功率;(3)求恒流源IS的功率。
例题5.开关S置位置1时电压表读数为4V,求开关S置位置2时电压表的读数。
例题6.将图(a)所示电路等效成图(b)所示的电压源。
要求
(1)计算等效电压源的Uou,Rab;
(2)若在ab之间接入一个电流表,计算电流表读数(不考虑电流表内阻对电路的影响);
(3)若在ab之间接入一个电阻R,当R获得最大功率时,计算R的值和最大功率Pmax。
例题7.电路如图(a)所示。
已知图(b)所示电路中,电流表的读数是2A;图(c)(d)所示电路中的电流I1、I2分别是0.5A和1A。
求
(1)A部分电路的等效电源参数Uso、Ro的值;
(2)R和Is的值;
(3)图(a)电路中5欧姆电阻的功率。
戴维南定理例题及答案1、解:将电阻R从电路中断开,如上左图。
显然,3Ω电阻和右侧的1A电流源变化为串联关系,所以3Ω电阻电流为1A。
对于节点n,KCL得到2Ω电阻电流:1+1=2(A)。
Uoc=Uab=Uan+Unb=1×3+2×2=7(V)。
将电压源短路、电流源开路,如上右图。
Req=Rab=3+2=5(Ω)。
最大功率传输定理:当R=Req=5Ω时,R获得最大功率,PLmax=Uoc²/(4R)=7²/(4×5)=2.45(W)。
解:原电路叠加定理:1、电压源作用时,电流源开路。
左上图。
电路电阻:R3+(R1+R2)∥R4=R+(R+R)∥2R=2R。
回路电流:I=(12-4)/2R=4/R,所以:U'=R×4/R=4(V)。
2、叠加定理的到:U"=U-U'=6-4=2(V)。
3、电流源单独激励,电压源短路,上中图,等效为上右图。
R1电压也为2V,则其电流为2/R,R4电流为1/R,KCL得到R2的电流为:2 /R+1/R=3/R,R2的电压为:R×3/R=3(V)。
R3两端电压:3+2=5V,电流为:5/R;Is=5/R+3/R=8/R。
电流源改变方向后的叠加:1、电压源作用时,响应不变:U'=4V。
2、电流源作用时,如右下图。
电流源外部总电阻:R3∥(R2+R1∥R4)=R∥(R +R∥2R)=5R/8。
端电压:(5R/8)×Is=(5R/8)×8/R=5(V),注意此时为下正上负。
并联支路的电流(即R2的电流):5/(R+R∥2R)=3/R,方向为从下向上。
所以:U"=-(3/R)×(R∥2R)=-2(V)。
实际上,这一步不用这么复杂的计算;包括原电路的Is(上面的步骤3、)也不用计算。
因为根据线性电路激励与相应的性质关系,直接可得到:Is反向后,新的U"等于原来U"的相反数。
对于任何一个含源二端网络都可以用一个电源来代替,其电源电动势E等于其含源二端网络的开路电压,其内阻R等于含源二端网络内所有电动势为零时的输入电阻,这就是戴维南定理.","force_purephv":"0","gnid":"92556239629d7cecd","highlight":{"ab_ta g_A":{"src":"kuaizixun_keywords_A","words":[{"index":50,"word":"内阻"},{"index":39,"word":"二端网络"},{"index":30,"word":"电动势"},{"index":21,"word":"电源"}]},"ab_tag_B":{"src":"kuaizixun_keywords_B","words":[{"index":50,"word ":"内阻"},{"index":39,"word":"二端网络"},{"index":30,"word":"电动势"},{"index":21,"word":"电源"}]}},"img_data":[{"flag":2,"img":[]}],"pat":"mass_model_adver,art_src_6,fts 2,sts0","powerby":"pika","pub_time":1574885731610,"rawurl":"http://zm. /ece8b7f69391c355ce27de98cb114a3b","redirect":0,"rptid": "611f0af7fbc1e915","src":"文学旅游生活","tag":[],"title":"戴维南定理的内容是什么?戴维南定理的例题_ :可将任一复杂的集总参数含源线性时不变二端网络等效为一个简单的二端网络的定理. 对于任意含独立源,线性电阻和线性受控源的单口网络(二端网络),都可以用一个电压源与电阻相串联的单口网络(二端网络)来等效.这个电压源的电压...戴维南定理例题:戴维南定理是一个很实用的定理.虽然这样的题,你可以一步一步简化这个电路图,最终得到最简的形式求得所需的电压值.(这题这样做样还简单一些)但是如果这个电路更复杂类似桥式电路,就无法用化简的方法直接求答案了,只能用戴维...用戴维南定理求习题7-20图所示电路中的电流I0. - 上学吧找答案:首先,找Rth(也就是R0)当找Rth时.所有线性时不变的电压源,视为短路(一条直线).R不考虑,因为R是负载,戴维南定律只看出了负载以外的电路.所以,当把48V和60V 换成直线之后,可以看到12ohm和6ohm的电阻成并联,并联求出...求助.戴维南定理解题步骤._ :运用戴维南定理解题的步骤概括为:1、分2、求E 3、求r 4、合分别配以相应的图形步骤(1) 把电路分为待求支路和有源二端网络两部分.(2) 把待求支路移开,求出有源二端网络的开路电压Uab (3) 将网络内各电源除去,仅保留电源内阻,求出网络两端的等效电阻Rab (4) 画出有源二端网络的等效电路,等效电路中电源的电动势E0=Uab,电源的内阻r0=Rab,然后在等效电路两端接入待求支路,则待求支路的电流为I= E0/( r0+R)【戴维南定理的内容以及解题步骤】:在计算戴维南等效电路时,必须联立两个由电阻及电压两个变量所组成的方程式,这两个方程式可经由下列步骤来获得: 1. 在AB两端开路(在没有任往外电流输出,亦即当AB点之间的阻抗无限大)的状况下计算输出电压VAB,此...戴维南定理是什么,解题步骤是哪些_ :戴维南等效是关于电压源的等效:故此:第一步:将待求电路与外电路断开,求待求电路等效端口处的开路电压;第二步:将待求电路中所有电压源短路(直接用导线短接代替),将所有电流源开路(直接断开),化解纯电阻电路,求得内阻.(注:含受控源可参考百度文档:应用戴维南定理求解线性含受控源电路) 第三步:根据求得的开路电压和内阻画出等效电路即可.戴维南定理题?_ :开路电压就是R0与R1分压, Uo=Us*R1/(R0+R1),等效电阻就是R0//R1,有了这个戴维南等效,计算I2和U就太容易了.。
戴维南定理基础练习题(打印版)# 戴维南定理基础练习题## 一、理论回顾戴维南定理(Thevenin's Theorem)是电路理论中的一个重要定理,它提供了一种将复杂电路简化为等效电路的方法。
根据戴维南定理,任何线性双端网络都可以用一个电压源和内阻串联的等效电路来代替。
### 1. 定理内容戴维南定理指出,对于任何线性双端网络,当其两端开路时,等效电压源的电压等于开路电压;当其两端短路时,等效内阻等于短路电流除以开路电压。
### 2. 应用条件- 电路必须是线性的。
- 电路两端可以是任意的两个节点。
## 二、基础练习题### 练习题1:开路电压与短路电流的计算题目描述:给定一个简单的电路,包含一个电压源Vs,一个电阻R1,和一个并联电阻R2。
计算开路电压和短路电流。
电路参数:- Vs = 10V- R1 = 1kΩ- R2 = 2kΩ解答:开路电压等于电压源的电压,即Voc = Vs = 10V。
短路电流Isc可以通过计算总电阻Rt得到:\[ R_t = \frac{R_1 \times R_2}{R_1 + R_2} = \frac{1k\Omega \times 2k\Omega}{1k\Omega + 2k\Omega} = 0.6667k\Omega \]\[ I_{sc} = \frac{V_s}{R_t} = \frac{10V}{0.6667k\Omega}\approx 15.01mA \]### 练习题2:等效电路的构建题目描述:在练习题1的基础上,构建等效电路,并计算当负载电阻RL = 3kΩ时的输出电压。
解答:等效电路由10V的电压源和0.6667kΩ的内阻串联组成。
当连接负载电阻RL时,总电阻为:\[ R_{total} = R_{th} + R_L = 0.6667k\Omega + 3k\Omega = 3.6667kΩ \]输出电压Vout可以通过欧姆定律计算:\[ V_{out} = I_{load} \times R_{total} \]\[ I_{load} = \frac{V_{oc}}{R_{total}} =\frac{10V}{3.6667k\Omega} \approx 2.73mA \]\[ V_{out} = 2.73mA \times 3.6667k\Omega \approx 10V \]### 练习题3:电路参数的调整题目描述:如果将练习题1中的R1改为2kΩ,重新计算开路电压和短路电流。
戴维南定理经典例题解析
戴维南定理是数论中的一个重要定理,它给出了一种判断一个整数是否为素数的方法。
该定理由英国数学家戴维南于1950年提出。
戴维南定理的表述为:如果一个整数N能够表示为N=a^2+b^2,其中a和b均为整数,那么N是素数的充分必要条件是N不能被4整除。
下面我们来看一个经典的例题解析。
例题:判断整数13是否为素数。
解析:根据戴维南定理,我们需要找到两个整数a和b,使得
13=a^2+b^2。
我们可以尝试不同的a和b的取值来验证。
当a=1时,b=3。
则13=1^2+3^2,符合定理的要求。
再来看另一个例子,当a=2时,b=3。
则13=2^2+3^2,依然符合定理的要求。
根据戴维南定理,我们得到13不能被4整除,因此13是素数。
总结:通过戴维南定理,我们可以判断一个整数是否为素数。
这个定理的证明较为复杂,需要使用到其他数学定理和方法。
在实际应用中,我们可以利用该定理来简化素数的判断过程。
戴维宁定理
一、知识点:
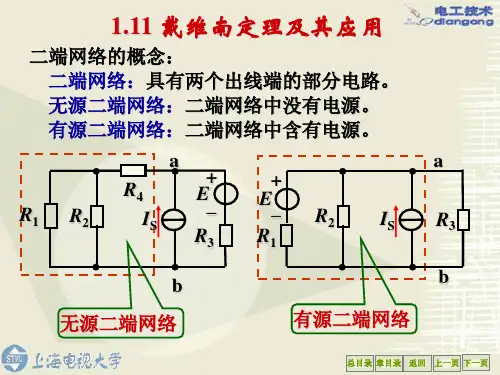
1、二端(一端口) 网络的概念:
二端网络:具有向外引出一对端子的电路或网络。
无源二端网络:二端网络中没有独立电源。
有源二端网络:二端网络中含有独立电源。
2、戴维宁(戴维南)定理
任何一个线性有源二端网络都可以用一个电压为U OC的理想电压源和一个电阻R0串联的等效电路来代替。
如图所示:
等效电路的电压U OC是有源二端网络的开路电压,即将负载R L断开后a 、b两端之间的电压。
等效电路的电阻R0是有源二端网络中所有独立电源均置零(理想电压源用短路代替,理想电流源用开路代替)后, 所得到的无源二端网络 a 、b两端之间的等效电阻。
二、 例题:应用戴维南定理解题:
戴维南定理的解题步骤:
1.把电路划分为待求支路和有源二端网络两部分,如图1中的虚线。
2.断开待求支路,形成有源二端网络(要画图),求有源二端网络的开路电压UOC 。
3.将有源二端网络内的电源置零,保留其内阻(要画图),求网络的入端等效电阻Rab 。
4.画出有源二端网络的等效电压源,其电压源电压US=UOC (此时要注意电源的极性),内阻R0=Rab 。
5.将待求支路接到等效电压源上,利用欧姆定律求电流。
例1:电路如图,已知U 1=40V ,U 2=20V ,R 1=R 2=4Ω,R 3=13 Ω,试用戴维宁定理求电流I 3。
解:(1) 断开待求支路求开路电压
U OC
U OC = U 2 + I R 2 = 20 +2.5 ⨯ 4 =
30V
或: U OC = U 1 – I R 1 = 40 –2.5 ⨯ 4 = 30V
U OC 也可用叠加原理等其它方法求。
(2) 求等效电阻R 0
将所有独立电源置零(理想电压源
用短路代替,理想电流源用开路代替)
(3) 画出等效电路求电流I 3
例2:试求电流 I 1
A 5.24420402121
=+-=+-=R R U U I Ω=+⨯=22
1210R R R R R A 213
23030OC 3=+=+=R R U I
解:(1) 断开待求支路求开路电压U OC
U OC = 10 – 3 ⨯ 1 = 7V
(2) 求等效电阻R 0
R 0 =3 Ω
(3) 画出等效电路求电流I 3
解得:I 1 = 1. 4 A
【例3】 用戴维南定理计算图中的支路电流I 3。
解:① 等效电源的电动势E 可由图1-58(b)求得
于是
或
② 等效电源的内阻R O 可由图1-58(c)求得
因此 3Ω +
_ 2Ω a
b I 1 7V
③ 对a和b两端讲,R1和R2是并联的,由图1-58(a)可等效于图1-58(d)。
所以
【例4】电路如图所示,R=2.5KΩ,试用戴维南定理求电阻R中的电流I。
解:图1-59(a)的电路可等效为图1-59(b)的电路。
将a、b间开路,求等效电源的电动势E,即开路电压U ab0。
应用结点电压法求a、b间开路时a和b两点的电位,即
将a、b间开路,求等效电源的内阻R0
R0=3KΩ//6KΩ+2KΩ//1KΩ//2KΩ=2.5KΩ
求电阻R中的电流I
三、应用戴维宁定理应注意的问题:
应用戴维南定理必须注意:
①戴维南定理只对外电路等效,对内电路不等效。
也就是说,不可应用该定理求出等效电源电动势和内阻之后,又返回来求原电路(即有源二端网络内部电路)的电流和功率。
②应用戴维南定理进行分析和计算时,如果待求支路后的有源二端网络仍为复杂电路,可再次运用戴维南定理,直至成为简单电路。
③使用戴维南定理的条件是二端网络必须是线性的,待求支路可以是线性或非线性的。
线性电路指的是含有电阻、电容、电感这些基本元件的电路;非线性电路指的是含有二极管、三极管、稳压管、逻辑电路元件等这些的电路。
当满足上述条件时,无论是直流电路还是交
流电路,只要是求解复杂电路中某一支路电流、电压或功率的问题,就可以使用戴维南定理。
四、练习题:
1、用戴维南定理求图中5Ω电阻中的电流I ,并画出戴维南等效电路
2、试用戴维南定理计算图示电路中3欧电阻中的电流I.(-35/31(A ))
3、试用戴维南定理计算图示电路中6欧电阻中的电流I 。
(0.75A )
4、如图中已知US1=140V US2=90V R1=20欧姆 R2=5欧姆 R3=6欧姆,用戴维宁定律计算电流 I 3 值 (10A )
5、计算图示电路中的电流I 。
(用戴维南定理求解)(2A )
- 10V + 6Ω
3Ω
3Ω 5A 2A - 20V +
题3图
6、计算图示电路中的电流I。
(用戴维南定理求解)(-1A)
7、计算图示电路中的电流I。
(用戴维南定理求解)
(1.6A)
7、用戴维南定理计算图中的支路电流I3。
(10A)
8、电路如图所示,R=2.5KΩ,试用戴维南定理求电阻R中的电流I。
(0.35 mA)
9、用戴维南定理求下图所示电路中的电流I(2A)。