通信原理第六章例
- 格式:pdf
- 大小:121.88 KB
- 文档页数:6


通信原理ICommunication Theory安建伟北京科技大学通信工程系第六章 数字信号的频带传输6.1 引言 6.2 二进制数字信号正弦型载波调制 6.3 四相移相键控 6.4 M进制数字调制 6.5 恒包络连续相位调制第6章数字信号的频带传输6.1 引言1.数字信号的正弦型载波调制数字信号 d(t) 调制 频带信号 带通信道s ( t ) = A c o s ( 2 π ft + ϕ ) = F ( d ( t ))用数字基带信号去控制正弦型载波的某参量: ¾ 控制载波的幅度,称为振幅键控(ASK); ¾ 控制载波的频率,称为频率键控(FSK); ¾ 控制载波的相位,称为相位键控(PSK)。
3北京科技大学通信系第6章数字信号的频带传输2. 数字信号的分类 (1)二进制及M进制(M>2); (2)按是否满足叠加原理分类: 线性调制及非线性调制; (3)按已调符号约束关系分类 无记忆调制及有记忆调制。
4北京科技大学通信系第6章数字信号的频带传输6.2 二进制数字信号的正弦载波调制1. 二进制通断键控(OOK或2ASK) 2. 二进制移频键控(2FSK) 3. 二进制移相键控(2PSK或BPSK) 4. 2PSK的载波同步 5. 差分移相键控(DPSK)5北京科技大学通信系第6章数字信号的频带传输 (OOK) 6.2.1 二进制通断键控二进制通断键控(OOK: On-Off Keying) 又名二进制振幅键(2ASK),它是以单极性 不归零码序列来控制正弦载波的导通与关 闭。
即正弦载波的幅度随数字基带信号而 变化。
6北京科技大学通信系第6章数字信号的频带传输1. OOK信号的产生a) 模拟法n = −∞∑+∞a nδ ( t − nTb )b (t ) =a n = 0 或1脉冲成形 滤波器 冲激响应 g T ( t )n = −∞∑+∞a n g T ( t − nTb )sO O K (t ) A cos(2π f c t )b) 键控法载波 cosωct开关电路1 0KSOOK(t)b(t)7北京科技大学通信系第6章数字信号的频带传输¾时域表示b( t ) =n = −∞∑a∞ngT ( t − nTb )其中b(t)为单极性矩形不归零脉冲序列。




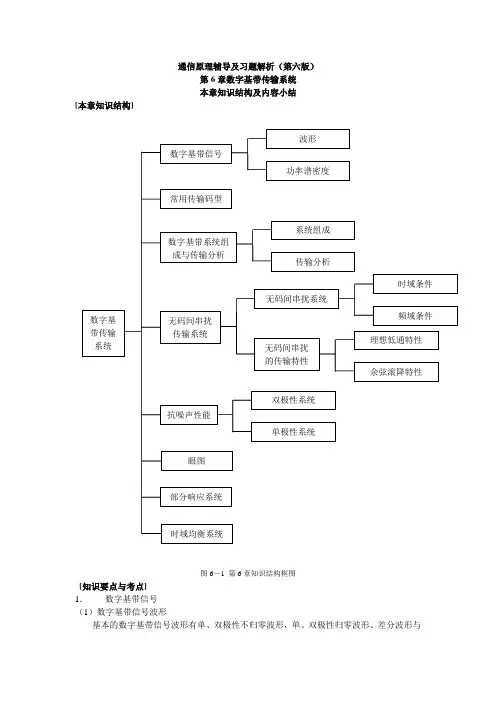
通信原理辅导及习题解析(第六版)第6章数字基带传输系统本章知识结构及内容小结[本章知识结构]图6-1 第6章知识结构框图[知识要点与考点]1.数字基带信号(1)数字基带信号波形基本的数字基带信号波形有单、双极性不归零波形,单、双极性归零波形、差分波形与多电平波形。
(2)数字基带信号的数学表达式 ①()()nsn s t a g t nT ∞=-∞=-∑式中,()s t 为单极性时,n a 取0或+1;()s t 为双极性时,n a 取+1或-1。
()g t 可取矩形 ②()()nn s t s t ∞=-∞=∑(3)数字基带信号的功率谱密度[]212212()(1)()()()(1)()()s s s s s s m P f f P P G f G f f PG mf P G mf f mf δ∞=-∞=--++--∑① 二进制数字基带信号的功率谱密度可能包含连续谱与离散谱。
其中,连续谱总是存在,根据连续谱确定信号带宽;在双极性等概信号时,离散谱不存在,根据离散谱确定直流分量与定时分量; ② 二进制不归零基带信号的带宽为s f (1/s s f T =);二进制归零基带信号的带宽为1/τ。
2.常用传输码型常用传输码型有三电平码(AMI 码、HDB3码)与二电平码(双相码、差分双相码、密勒码、CMI 码、块编码)。
其中,AMI 码与HDB3码需要重点掌握。
(1)AMI 码将消息码的“1”(传号)交替地变换为“+1”和“-1”,而“0”(空号)保持不变。
(2)HDB3码 ① 编码规则:当连0数目不超过3个时,同AMI 码;连0数目超过3时,将每4个连“0”化作一小节,定义为B00V ;V 与前一个相邻的非0脉冲极性相同,相邻的V 码之间极性交替。
V 的取值为+1或-1;B 的取值可选0、+1或-1;V 码后面的传号码极性也要交替。
② 译码规则:寻找破坏脉冲V 码,即寻找两个相邻的同极性码,后一个码为V 码;V 码与其之前的3个码一起为4个连0码;将所有-1变成+1后便得到原消息代码。


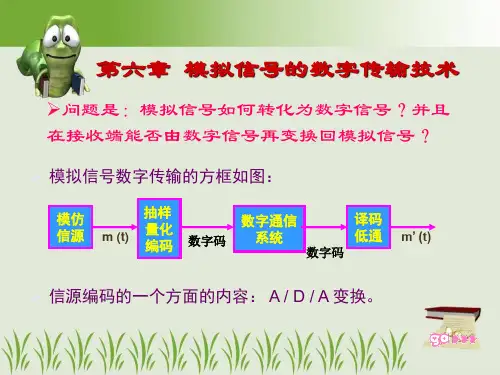
第六章(模拟信号的数字传输)习题及其答案【题6-1】已知信号()m t 的最高频率为m f ,由矩形脉冲()m t 进行瞬时抽样,矩形脉冲的宽度为2τ,幅度为1,试确定已抽样信号及其频谱表示式。
【答案6-1】矩形脉冲形成网络的传输函数()()()22Q A Sa Sa ωτωτωττ==理想冲激抽样后的信号频谱为1()(2) =2s mm m n sM M n f T ωωωωπ∞=-∞=-∑瞬时抽样信号频谱为()()()()(2)2H s m n sM M Q Sa M n T τωτωωωωω∞=-∞==-∑()H M ω中包括调制信号频谱与原始信号频谱()M ω不同,这是因为()Q ω的加权。
瞬时抽样信号时域表达式为()()()()H sn m t m t t nT q t δ∞=-∞=-*∑【题6-2】设输入抽样器的信号为门函数()G t τ,宽度200ms τ=,若忽略其频谱的第10个零点以外的频率分量,试求最小抽样速率。
【答案6-2】门函数()G t τ的宽度200ms τ=,其第一个零点频率1150f Hz τ==,其余零点之间间隔都是1τ,所以第10个零点频率为110500m f f Hz ==。
忽略第10个零点以外的频率分量,门函数的最高频率是500Hz 。
由抽样定理,可知最小抽样速率21000s m f f Hz ==。
【题6-3】设信号()9cos m t A t ω=+,其中10A V =。
若()m t 被均匀量化为40个电平,试确定所需的二进制码组的位数N 和量化间隔v ∆。
【答案6-3】()m t 需要被量化为40个电平,即40M =,表示40个电平需要的二进制码组位数2[log ]16N M =+=量化间隔22100.540A v V M ⨯∆===【题6-4】已知模拟信号抽样的概率密度()f x 如下图所示。
若按四电平进行均匀量化,试计算信号量化噪声功率比。
1第一部分AMI码与HDB3码对传输用的基带信号的主要要求:对代码的要求:原始消息代码必须编成适合于传输用的码型;对所选码型的电波形要求:电波形应适合于基带系统的传输。
1. AMI码(传号交替反转码)编码规则:传号(“1”)极性交替,空号(“0”)不变。
例:信码{an}: 1 0 1 0 0 1 0 0 0 0 0 1 0 1 AMI: +1 0 -1 0 0 +1 0 0 0 0 0 -1 0 +1特点:(1)无直流分量和仅有小的低频分量;(2)二电平→三电平--1B/1T码(一个二进制符号变换成一个三进制符号所构成的码);(3)易于检错;(4)编、译码简单;(5)当出现长的连0串时,不利于定时信息的提取。
1.00.5s2. HDB3码编码规则:(1)当连“0”个数不超过3时,仍按AMI码的规则编,即传号极性交替;(2)当连“0”个数超过3时,4个连“0”为一组,当该组四连“0”与其前一组四连“0”之间有奇数个传号码,用000V取代该组四连“0”。
V 极性与其前非零码极性一致,V本身满足极性交替;(3)当该组四连“0”与其前一组四连“0”之间有偶数个(包括0个)传号码,用B00V取代该组四连“0”。
B极性与其前一非零码极性相反,V极性与B极性一致,V本身满足极性交替;例如:1 1 0 0 0 0 1 1 1 0 0 0 0 0 1HDB3 +V -1 +1 -B 0 0 -V +1 -1 +1 0 0 0 +v 0 +1 译码:凡遇到-1 0 0 0 -1+1 0 0 0 +1+1 0 0 +1-1 0 0 -1译成:*0 0 0 0例:HDB3:0 +1 0 0 0 +1 -1+1 -1 0 0 -1 0 +1 0 -1代码:0 1 0 0 0 0 1 1 0 0 0 0 0 1 0 1特点:1)无直流分量、低频分量小;2)连0串不会超过3个,对定时信号的恢复十分有利;3)编码复杂,译码简单。
第六章例题
第六章重点:
1、抽样定理:低通和带通抽样定理。
2、均匀量化:
令量化器动态范围为-V~+V ,量化电平数为M ,则量化间隔为:M
V
2=Δ最大量化误差为:M
V ±=Δ2若量化器输入信号的实际动态范围为-a~+a ,则必
须满足a<=V ,否则会产生过载量化噪声。
在均匀量化且不过载的情况下量化噪声功率为:
2
22
312M V N q =
Δ=输入信号均匀分布时的量化信噪比:
2M N S
q
=N
dB M N S
N N q 02.6)(2log 102222====所以PCM 编码组每增加1位,等效于量化信噪比增加6dB 。
虽然上式是在输入信号均匀分布条件下得到的,但是对于正弦、语音等信号也有类似结论。
3、非均匀量化
含义:量化间隔不均匀的量化;
目的:提高小信号时的量化信噪比;代价:牺牲大信号时的量化信噪比;实现:非线性压缩+均匀量化;
例题1、设模拟信号m(t)的频谱为M(f);
⎩⎨
⎧>≤−= 1000Hz 0
1000Hz 1000/2)(f f f f M ,
,画出M(f)的频谱,说明对抽样率的要求。
解:注意M(f)在|f|=1000Hz 时有值1,所以抽样速率必须满足f s >2000Hz 。
当f s <=2000Hz 时会出现混叠。
1
f/KHz
M(f)
1
-1
例题2、一模拟信号的幅度范围为-10V~+10V ,最高频率为f H =1kHz 。
现对其进行线性PCM 传输,若要求量化误差不超过动态范围的±0.1%。
试求:
(1)最低抽样速率;
(2)每个PCM码子所需的最小比特数;(3)该PCM码子所需的最低比特率;
(4)为传输该PCM码子所需的最小理论带宽;
解:
(1)f smin =2f H =2kHz
(2) 量化误差不超过动态范围的±0.1%;动态范围为20V ,量化误差为:所以,有:
M V
=Δ21
/200.1%0.1%22500
V M M Δ≤⇔≤⇒≥所以取M=512,于是N=9。
(4)由于频带利用率最大为2bit/HZ ,所以有
)
/(1829min min s kbit kHz Nf R s b =×==)
(92
kHz R B b
==(3)
例题3、采用13折线A 律编码,归一化1分为2048个量化单位Δ。
设输入信号样值x 为+308Δ。
求:
(1)编码器输出码组。
(2)译码输出和量化误差。
解:1、极性码为正所以c1=1。
2、由于308>128,所以x 处于8段中后四段。
C2=1。
由于308<512,所以x 处于第五第六段,c3=0;又由于308>256,所以x 出来第六段。
C4=1;因此,段落码c2c3c4=101,x 处于第六段:256~512.
3、段内码均匀划分,Δi =16 Δ。
由于308<384,所以c5=0;且308<320,所以c6=0;
由于308>288,所以c7=1;又由于308>304,所以c8=1;因此段内码c5c6c7c8=0011;最后可得+308 Δ的编码为11010011
2、译码:A 、译码结果:
对应的译码结果为+304 Δ;译码结果就是对码组直接译码得到的结果。
B 、译码输出:译码结果再加上Δi /2。
所以译码输出为+(304+16/2) Δ=+312 Δ。
C 、量化误差:
q=x-x q =+308-(+312)=-4 Δ
为什么译码输出要加上Δi /2?
本题中,当输出x 处于304~320区间内都会被编码成11010011,而他们的译码结果都是304,所以误差为0~16。
最大量化误差为16。
当加上Δi /2后,译码输出变为312,于是误差在-8~+8范围内。
当然后者要好。
例题4、(1)采用13折线A 律编码,归一化1分为2048个量化单位Δ。
设输入信号值x 为+240 Δ,求编码器输出码组。
(2)若改为线性PCM 编码,仍编为8bit ,且工作范围仍为±2048Δ,再求编码器输出码组。
(3)对上面两种情况的量化信噪比做比较。
解:1、极性码为正,所以c1=1;由于128<x<256,所以得段落码为c2c3c4=100,即x 处于第5段:128~256。
Δi =8。
再由128+n Δi <=240,得n=14=(1110)2;所以可得:
编码器输出C=11001110。
(2)线性PCM 编码时:极性码也是c1=1;段落码均匀划分,所以每段间隔为2048/8=256.由于240<256,所以处于第1段。
即段落码为000;
第1段内均匀16分割,可得每段为256/16=16。
由n Δi<=240,可得n=(15)10=(1111)2;所以最后编码输出为C=10001111。
(3)量化噪声功率为
第一题中Δi =8,第二题中Δi =16因此13折线法有更小的量化噪声功率。
当输入信号相同时,13折线法能获得更高的量化信噪比。
12
2
Δ=
q N 例题5、设模拟信号m(t)的幅值在[-2,+2]V 内均匀分布,最高频率为4kHz ,现对其进行奈奎斯特速率抽样,并经均匀量化后编为二进制码。
设量化间隔为1/64V ,试求:(1)该PCM 系统的信息速率;(2)量化信噪比;
例7、已知话音信号的最高频率f
为3400Hz,今
m
用PCM系统传输,要求量化信噪比不低于
30dB,试求此时PCM系统所需的最小带宽。
解:1、
2、
α
ω⇒。