线段与角的有关计算

长度与角度的计算1.长度的计算：长度是指物体所占据的空间距离。

在几何学中，我们常常需要计算线段、弧长、周长等长度相关的内容。

1.1线段长度的计算：线段是由两个点所确定的一段直线，在计算线段长度时，我们可以利用线段的坐标或者使用勾股定理进行计算。

例如，对于坐标系中的两个点P₁(x₁,y₁)和P₂(x₂,y₂)，线段的长度可以使用以下公式进行计算：L = sqrt((x₂ - x₁)² + (y₂ - y₁)²)1.2弧长的计算：弧是圆周上的一部分，弧长是弧所占据的圆周的长度。

弧长的计算涉及到圆周率π和圆的半径r。

对于半径为r的圆的弧长L，可以使用以下公式进行计算：L=2πr1.3周长的计算：周长是封闭曲线（如矩形、圆形等）的长度。

对于不同形状的封闭曲线，周长的计算方法略有不同。

例如，对于矩形的周长P，可以使用以下公式进行计算：P=2(a+b)，其中a和b分别表示矩形的两条边的长度2.角度的计算：角度是两条射线之间的夹角。

角可以用度（°）或弧度（rad）来表示。

在几何学中，我们常常需要计算角的度数，以及角度之间的关联。

2.1角的度数计算：角的度数计算常常基于一个完整的圆的圆周角为360°，即一周的角度为360°。

根据这一原则，我们可以计算出其他角度的度数。

例如，对于直角角度为90°，平角角度为180°，关于这些基本角度，我们可以使用加法和减法运算来计算其他角度的度数。

2.2角度的关联性：角度可以通过三角函数来进行计算。

三角函数（如正弦、余弦、正切等）是角度与三角比之间的关系。

我们可以使用三角函数来计算角的度数、角的正弦、余弦、正切等。

在计算中，有一些常用的角度关联公式，例如：-三角形内角的和：在一个三角形中，三个内角的和等于180°。

-角的补角：两个角的补角之和为90°。

-角的余角：两个角的余角之和为90°。

线段和角度的计算线段和角度是几何学中基础而重要的概念，对于几何学的研究和实际应用具有重要的意义。

本文将介绍线段和角度的计算方法，并且提供一些实例来帮助读者更好地理解。

一、线段的计算线段是几何学中最基础的图形，其长度的计算是几何学中最常见的问题之一。

计算线段的长度需要知道线段的两个端点的坐标，然后根据坐标计算两个点之间的距离即可。

假设线段的两个端点的坐标分别为A(x1, y1)和B(x2, y2)，则线段AB的长度可以使用以下公式计算：AB = √[(x2-x1)^2 + (y2-y1)^2]其中√代表求平方根。

举例来说，如果线段的一个端点坐标为A(2, 3)，另一个端点坐标为B(5, 7)，则线段AB的长度可以计算如下：AB = √[(5-2)^2 + (7-3)^2]= √[3^2 + 4^2]= √[9 + 16]= √25= 5因此，线段AB的长度为5。

二、角度的计算角度是描述两条相交线之间关系的概念，它是几何学中重要的衡量单位。

计算角度需要知道角的顶点和两条边的坐标，然后通过计算得出角的度数。

假设角的顶点坐标为O(x0, y0)，边OA的坐标为A(x1, y1)，边OB 的坐标为B(x2, y2)，则角AOB的度数可以使用以下公式计算：θ = arccos[(OA·OB)/(|OA|·|OB|)]其中arccos代表反余弦函数，|OA|和|OB|代表OA和OB的长度，·表示点乘运算（坐标相乘后相加）。

举例来说，如果角AOB的顶点坐标为O(0, 0)，边OA的坐标为A(1, 2)，边OB的坐标为B(3, 4)，则角AOB的度数可以计算如下：θ = arccos[((1-0)(3-0) + (2-0)(4-0))/((√[(1-0)^2 + (2-0)^2])*(√[(3-0)^2 + (4-0)^2]))]= arccos[(3+8)/(√(1+4) * √(9+16))]= arccos[11/(√5 * √25)]≈ arccos(0.9806)≈ 0.1944 radians因此，角AOB的度数约为0.1944弧度。

学习数学中的线段和角度计算数学是一门既抽象又实用的学科，线段和角度计算是数学中基础且重要的概念。

学好线段和角度的计算对于后续的数学学习和实际问题的解决都至关重要。

本文将详细介绍线段和角度的计算方法及其应用。

一、线段计算在数学中，线段是指由两个点A和B组成的线段AB。

对于线段的计算，常见的问题有计算线段的长度、线段的中点以及两个线段的关系等。

1. 计算线段的长度计算线段的长度是最常见的线段计算问题。

假设有线段AB，其中A的坐标为(x1, y1)，B的坐标为(x2, y2)，则根据勾股定理，线段AB的长度L可通过以下公式计算：L = √((x2-x1)² + (y2-y1)²)其中（x2-x1）和（y2-y1）分别代表AB线段在x轴和y轴方向上的投影长度。

2. 计算线段的中点线段的中点是线段的重要属性，它的坐标可以通过线段的两个端点坐标求得。

假设线段AB的中点坐标为M(x,y)，A的坐标为(x1, y1)，B的坐标为(x2, y2)，则M的坐标可以通过如下公式计算：x = (x1+x2)/2y = (y1+y2)/23. 判断两个线段的关系当需要判断两个线段的关系时，可以从以下几个方面进行考虑。

- 首先，可以计算两个线段的长度。

如果两个线段的长度相等，则可以判断它们是相等的线段。

- 其次，可以计算两个线段的斜率。

如果两个线段的斜率相等，则可以判断它们是平行的线段。

- 最后，可以比较两个线段的垂直距离和水平距离。

如果两个线段之间的水平距离和垂直距离都为零，则可以判断它们是重合的线段。

二、角度计算在数学中，角度是指由两条射线组成的形状。

角度的计算是数学中的重要内容，常见的问题包括计算角度的大小和正余弦等。

1. 计算角度的大小计算角度的大小需要根据角度所涉及的几何图形进行计算。

常见的几何图形包括直角三角形、等边三角形等。

对于直角三角形，可以通过已知的两条边长计算角度的大小。

而对于等边三角形，则可以通过已知的一个边长计算角度的大小。

线段与角的概念和计算一、线段的概念线段是几何学中的基本概念之一，它是指由两个端点确定的具有有限长度的直线部分。

在平面几何中，线段用两个大写字母表示，如AB、CD等。

线段的长度通常用小写字母表示，如|AB|表示线段AB的长度。

二、角的概念角是点和其两条射线组成的图形，通常用希腊字母表示，如∠ABC，其中B为角的顶点，而A、C分别为角的两个边。

角度可以用度数（°）或弧度（rad）表示，度数是人们最常用的度量单位。

三、线段的计算1. 线段的长度线段的长度可以通过两个端点的坐标计算得出。

设线段AB的两个端点坐标分别为A(x₁, y₁)和B(x₂, y₂)，则线段AB的长度可以通过以下公式计算：|AB| = √((x₂ - x₁)² + (y₂ - y₁)²)2. 线段的中点线段的中点是指线段的中心位置，在平面几何中也是一个重要的概念。

设线段AB的两个端点坐标分别为A(x₁, y₁)和B(x₂, y₂)，则线段AB的中点坐标可以通过以下公式计算：M((x₁ + x₂)/2, (y₁ + y₂)/2)四、角的计算1. 角度角度是人们常用的度量单位，一周等于360°。

当需要计算角度时，可以利用以下公式来进行计算：角度 = 弧长 / 半径2. 弧度弧度是另一种常用的角度单位，它是圆周上弧长等于半径的一部分。

当需要计算弧度时，可以利用以下公式来进行计算：弧度 = 弧长 / 半径3. 弧度与角度的转换弧度与角度之间可以通过以下公式进行转换：角度 = 弧度× 180° / π弧度 = 角度× π / 180°五、实例应用为了更好地理解线段与角的概念和计算方法，以下通过一个实例进行说明。

假设有一条线段AB，其中A(-2, 3)和B(4, -1)分别为线段的两个端点坐标。

我们首先可以计算线段AB的长度：|AB| = √((4 - (-2))² + ((-1) - 3)²)= √(6² + (-4)²)= √(36 + 16)= √52≈ 7.211然后我们可以计算线段AB的中点坐标：M(((-2) + 4)/2, (3 + (-1))/2)≈ M(1, 1)接下来我们可以计算角ADC的度数。

线段与角的和差倍分计算
在几何学中，我们经常遇到线段与角之间的和、差和倍分计算问题。

这些计算方法是为了帮助我们更好地理解图形的性质和关系。

本文将详细
介绍线段与角之间的和、差和倍分计算方法。

一、线段的和、差计算
1.线段的和计算：给定线段AB和线段BC，我们需要计算出两个线段
的和，即线段AB+BC。

计算方法是将线段AB和BC的长度相加，即AB+BC。

2.线段的差计算：给定线段AB和线段BC，我们需要计算出两个线段
的差，即线段AB-BC。

计算方法是将线段AB的长度减去线段BC的长度，
即AB-BC。

二、角的和、差计算
1.角的和计算：给定角α和角β，我们需要计算出两个角的和，即
角α+角β。

计算方法是将两个角的度数相加，即α+β。

2.角的差计算：给定角α和角β，我们需要计算出两个角的差，即
角α-角β。

计算方法是将角α的度数减去角β的度数，即α-β。

三、线段与角的倍分计算
1.线段的倍分计算：给定线段AB，我们需要计算出线段AB的一半或
一四分之一的长度。

计算方法是将线段AB的长度除以2或4，即AB/2或AB/4
2.角的倍分计算：给定角α，我们需要计算出角α的一半或一四分
之一的度数。

计算方法是将角α的度数除以2或4，即α/2或α/4
以上是线段与角的和、差和倍分计算的基本方法。

在实际应用中，我们还可以利用一些几何定理和性质来简化计算，例如角的补角、互补角和对应角等关系。

线段与角的计算线段和角是几何学中常见的概念，它们在解决各种几何问题中起着重要的作用。

本文将介绍线段和角的计算方法，并通过例子详细说明其应用。

一、线段的计算线段是两点之间的直线部分，其长度可通过坐标、勾股定理或其他方法进行计算。

1. 坐标计算法设在笛卡尔坐标系中，已知两点A(x₁, y₁)和B(x₂, y₂)，则线段AB的长度计算公式为：d = √((x₂ - x₁)² + (y₂ - y₁)²)其中，d表示线段AB的长度。

例如，已知点A(2, 3)和点B(5, 7)，则线段AB的长度为：d = √((5 - 2)² + (7 - 3)²)= √(3² + 4²)= √(9 + 16)= √25= 5因此，线段AB的长度为5。

2. 勾股定理勾股定理是用于计算直角三角形的边长的常用方法。

当线段确定为直角三角形的一条边时，可以使用勾股定理来计算其长度。

设直角三角形的一条直角边长为a，另外两条边分别为b和c，则勾股定理可以表示为：a² = b² + c²根据这个公式，可以计算出线段的长度。

例如，已知直角三角形的两条边分别为5和12，求第三边的长度。

根据勾股定理，可得：a² = 5² + 12²= 25 + 144= 169因此，直角三角形的第三边长度为√169，即13。

二、角的计算角是由两条射线共享一个端点形成的图形，可以通过度数或弧度来进行计算。

1. 度数计算法角的度数计算方法包括以下几种：(1) 已知两条射线的坐标，可以通过坐标计算得出角的度数。

例如，已知射线OA和射线OB，可以通过计算斜率、弧度或反三角函数来得到角的度数。

(2) 已知角的度数，可以通过度数的加减乘除来计算其他角度。

例如，已知角AOB的度数为50°，求角BOC的度数，若角COB为直角，求角AOC的度数。

2. 弧度计算法弧度是计量角度的单位，用于计算圆周上的弧长。

线段和角是几何中的基本概念，它们在解决实际问题中起到了至关重要的作用。

在七年级的学习中，我们将学习如何计算线段的长度和角的度数。

本文将详细介绍线段和角的有关计算知识，包括线段的计算方法、角的计算方法，以及一些实际问题的解决方法。

一、线段的计算方法线段是连接两个点的直线部分，它具有长度。

在计算线段的长度时，我们需要了解两个点的坐标，并且应用勾股定理。

勾股定理表述如下：在直角三角形中，直角边的平方等于两直角边的平方之和。

根据勾股定理，我们可以求得两点之间的距离。

例如，有一个线段AB，它的两个端点的坐标分别为A(x1,y1)和B(x2,y2)。

我们可以通过以下公式计算AB的长度：AB=√[(x2-x1)²+(y2-y1)²]这个公式非常简单，只需要知道两个点的坐标，即可计算出线段的长度。

下面，我们来看一个实际问题的例子。

例题：在平面直角坐标系中，有两点A（2，3）和B（5，6），求线段AB的长度。

解答：根据上面的公式，我们可以求得线段AB的长度：AB=√[(5-2)²+(6-3)²]=√[3²+3²]=√[18]≈4.24所以，线段AB的长度约为4.24二、角的计算方法角是由两条线段的交汇形成的。

在计算角的度数时，我们需要了解两条线段的向量，并且应用向量的运算。

对于两个向量u=(x1,y1)和v=(x2,y2)，它们的夹角θ可以通过以下公式计算：cosθ = (x1 * x2 + y1 * y2) / (√[x1² + y1²] * √[x2² + y2²])最终的角度可以通过反余弦函数来求得：θ = arccos(cosθ)这个公式非常实用，只需要知道两个向量的坐标，即可计算出角的度数。

下面，我们来看一个实际问题的例子。

例题：在平面直角坐标系中，有两条线段AB和AC，它们的坐标分别为A（1，2）、B（4，6）和C（7，3），求角BAC的度数。

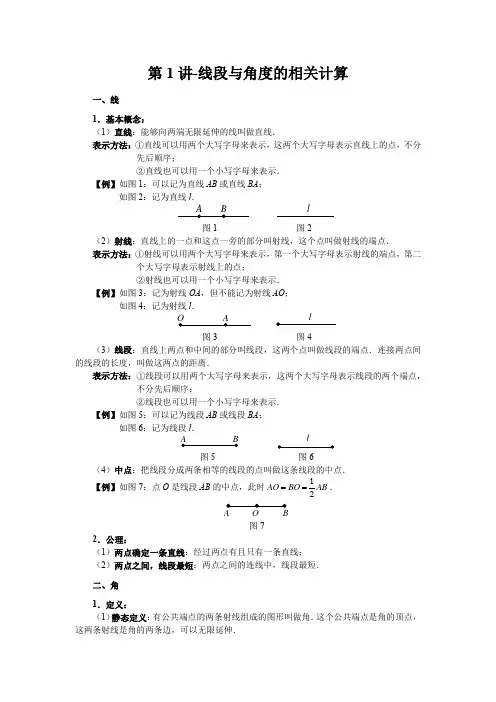
第1讲-线段与角度的相关计算一、线1．基本概念：（1）直线：能够向两端无限延伸的线叫做直线．表示方法：①直线可以用两个大写字母来表示，这两个大写字母表示直线上的点，不分先后顺序；②直线也可以用一个小写字母来表示．【例】如图1：可以记为直线AB 或直线BA ；如图2：记为直线l ．图1 图2（2）射线：直线上的一点和这点一旁的部分叫射线，这个点叫做射线的端点．表示方法：①射线可以用两个大写字母来表示，第一个大写字母表示射线的端点，第二个大写字母表示射线上的点；②射线也可以用一个小写字母来表示．【例】如图3：记为射线OA ，但不能记为射线AO ；如图4：记为射线l ．图3 图4（3）线段：直线上两点和中间的部分叫线段，这两个点叫做线段的端点．连接两点间的线段的长度，叫做这两点的距离．表示方法：①线段可以用两个大写字母来表示，这两个大写字母表示线段的两个端点，不分先后顺序；②线段也可以用一个小写字母来表示．【例】如图5：可以记为线段AB 或线段BA ；如图6：记为线段l ．图5 图6（4）中点：把线段分成两条相等的线段的点叫做这条线段的中点．【例】如图7：点O 是线段AB 的中点，此时AO BO AB 1==2．图72．公理：（1）两点确定一条直线：经过两点有且只有一条直线； （2）两点之间，线段最短：两点之间的连线中，线段最短． 二、角1．定义： （1）静态定义：有公共端点的两条射线组成的图形叫做角．这个公共端点是角的顶点，这两条射线是角的两条边，可以无限延伸．llA O (5) l A B(6)l（2）动态定义：由一条射线绕着它的端点旋转到另一个位置所成的图形叫做角．处于初始位置的那条射线叫做角的始边，终止位置的那条射线叫做角的终边．表示方法：①通常用三个字母表示：两条边上的点的字母写在两旁，顶点上的字母写在中间．②用一个大写字母来表示：这个大写字母一定要表示角的顶点，而且以它为顶点的角只有一个．③用数字或希腊字母来表示：可以用希腊字母（α，β，γ，θ，ϕ, ...）表示角的大小。

线段与角的计算1.已知：如图，点M 、N 分别是线段AB 、BC 的中点，且AB ＝a ㎝，BC ＝b ㎝. 求：线段MN 的长.解：∵点M 、N 分别是线段AB 、BC 的中点，且AB ＝a ㎝，BC ＝b ㎝.∴BM ＝21AB ＝21a ㎝，BN ＝21BC ＝21b ㎝, ∴MN ＝BM ＋BN ＝21( a ＋b ) ㎝. 即线段MN 的长为21( a ＋b ) ㎝.2. 已知：如图，射线OM 、ON 分别是∠AOB 、∠BOC 的角平分线，且∠AOB ＝α，∠BOC ＝β.求： ∠MON 的度数.解：∵OM 、ON 分别是∠AOB 、∠BOC 的角平分线，且∠AOB ＝α，∠BOC ＝β.∴∠BOM ＝21∠AOB ＝21α ，∠BON ＝21∠BOC ＝21β, ∴∠MON ＝∠BOM ＋∠BON ＝21( α＋β). 即∠MON 的度数为21( α＋β).3.已知：如图，点M 、N 分别是线段AB 、BC 的中点，且AB ＝a ㎝，BC ＝b ㎝. 求：线段MN 的长.O解：∵点M 、N 分别是线段AB 、BC 的中点，且AB ＝a ㎝，BC ＝b ㎝.∴BM ＝21AB ＝21a ㎝，BN ＝21BC ＝21b ㎝, ∴MN ＝BM －BN ＝21( a －b ) ㎝. 即线段MN 的长为21( a －b ) ㎝.4. 已知：如图，射线OM 、ON 分别是∠AOB 、∠BOC 的角平分线，且∠AOB ＝α，∠BOC ＝β.求： ∠MON 的度数.解：∵OM 、ON 分别是∠AOB 、∠BOC 的角平分线，且∠AOB ＝α，∠BOC ＝β. ∴∠BOM ＝21∠AOB ＝21α ，∠BON ＝21∠BOC ＝21β,∴∠MON ＝∠BOM －∠BON ＝21( α－β). 即∠MON 的度数为21( α－β).5.已知：如图，点C 在线段AB 上，点M 、N 分别是线段AB 、BC 的中点，且AC ＝a ㎝，BC ＝b ㎝. 求：线段MN 的长.解：∵点M 、N 分别是线段AB 、BC 的中点，且AC ＝a ㎝，BC ＝b ㎝.O222BN ＝21BC ＝21b ㎝,∴MN ＝BM －BN ＝21( a ＋b )－21b ＝21a ㎝. 即线段MN 的长为21a ㎝.6. 已知：如图，射线OM 、ON 分别是∠AOC 、∠BOC 的角平分线，且∠AOB ＝α，∠BOC ＝β.求： ∠MON 的度数.解：∵OM 、ON 分别是∠AOC 、∠BOC 的角平分线，且∠AOB ＝α，∠BOC ＝β. ∴∠COM ＝21∠AOC ＝21(∠AOB ＋∠BOC )＝21(α＋β)，∠CON ＝21∠BOC ＝21β,∴∠MON ＝∠COM －∠CON ＝21( α＋β)－21β＝21α. 即∠MON 的度数为21α.7.已知：如图，点C 在线段AB 上，点M 、N 分别是线段AB 、AC 的中点，且AC ＝a ㎝，BC ＝b ㎝. 求：线段MN 的长.解：∵点M 、N 分别是线段AB 、AC 的中点，且AC ＝a ㎝，BC ＝b ㎝.O222AN ＝21AC ＝21a ㎝,∴MN ＝AM －AN ＝21( a ＋b )－21a ＝21b ㎝. 即线段MN 的长为21b ㎝.8. 已知：如图，射线OM 、ON 分别是∠AOC 、∠AOB 的角平分线，且∠AOB ＝α，∠BOC ＝β.求： ∠MON 的度数.解：∵OM 、ON 分别是∠AOC 、∠AOB 的角平分线，且∠AOB ＝α，∠BOC ＝β.∴∠AOM ＝21∠AOC ＝21(∠AOB ＋∠BOC )＝21(α＋β)，∠AON ＝21∠AOB ＝21α,∴∠MON ＝∠AOM －∠AON ＝21( α＋β)－21α＝21β. 即∠MON 的度数为21β.9.已知：如图，点C 、D 在线段AB 上，点M 、N 分别是线段AC 、BD 的中点，且AB ＝a ㎝，CD ＝b ㎝. 求：线段MN 的长.解：∵点M 、N 分别是线段AC 、BD 的中点，∴CM ＝21AC ，DN ＝21BD , ∵AB ＝a ㎝，CD ＝b ㎝,∴CM ＋DN ＝21(AC ＋BD )＝21(AB －CD ) ＝21(a －b ) ㎝,∴MN ＝CM ＋CD ＋DN ＝21(a －b )－b ＝21(a ＋b ) ㎝. 即线段MN 的长为21(a ＋b ) ㎝.10. 已知：如图，射线OM 、ON 分别是∠AOC 、∠BOD 的角平分线，且∠AOB ＝α，∠COD ＝β.求： ∠MON 的度数.解：∵OM 、ON 分别是∠AOC 、∠BOD 的角平分线，∴∠COM ＝21∠AOC ，∠DON ＝21∠BOD , ∵∠AOB ＝α，∠COD ＝β，∴∠COM ＋∠DON ＝21(∠AOC ＋∠BOD )＝21(∠AOB －∠COD ) ＝21(α－β),∴∠MON ＝∠COM ＋∠COD ＋∠DON ＝21( α－β)＋β＝21( α＋β). 即∠MON 的度数为21( α＋β).。

线段的长度与角度线段是几何学中的基本概念之一，是由两个端点确定的一条直线的部分。

在几何学中，线段的长度与角度是两个重要的量，它们在实际生活和学术研究中都具有广泛的应用。

本文将探讨线段的长度和角度之间的关系，并介绍一些相关的数学公式和实际应用。

一、线段的长度线段的长度是指线段所占据的空间距离，通常用单位长度（如米、厘米）来表示。

在几何学中，我们可以使用勾股定理来计算线段的长度。

勾股定理表示在直角三角形中，斜边的平方等于两条直角边的平方之和。

例如，对于一个直角三角形，如果已知两条直角边的长度分别为a和b，斜边的长度即为c，根据勾股定理，可以得到c的计算公式：c = √(a² + b²)这个公式可以用来计算任意两点之间的距离，从而计算线段的长度。

在实际应用中，勾股定理在测量、建筑、导航等领域有着广泛的应用。

二、线段的角度线段的角度是指线段相对于某个参考方向的偏转角度。

角度通常用度数或弧度来表示。

在几何学中，我们通常使用角度来描述旋转、方向和位置等概念。

在平面几何中，我们可以使用三角函数来计算角度。

对于一个直角三角形，已知两条直角边的长度分别为a和b，角度的计算公式如下：sinθ = a / ccosθ = b / ctanθ = a / b其中，θ表示角度的大小，sin、cos和tan分别表示三角函数的值。

通过这些公式，我们可以根据已知的两条直角边的长度来计算角度的大小。

三、线段长度与角度的关系线段的长度和角度之间存在着一定的关系。

当线段的长度增大时，相同角度的线段在空间中所占据的区域也会增大。

反之，当线段的角度增大时，相同长度的线段在空间中所占据的区域也会增大。

具体来说，当线段的长度为固定值时，可以通过改变线段的角度来改变线段所占据的空间区域的形状。

例如，在建筑设计中，人们常常需要根据不同的空间需求来设计不同形状的房间。

通过改变房间的线段长度和角度，可以实现房间形态的差异化。

另外，线段的长度和角度还与线段的直观感受相关。

1.利用几何的直观性，寻找所求量与已知量的关系2.利用线段中点性质，进行线段长度变换3. 根据图形及已知条件，利用解方程的方法求解线段与角的计算及解题方法求线段长度的几种常用方法：例 1. 如图1 所示，点C 分线段AB 为5：7，点D 分线段AB 为5：11，若CD＝10cm，求AB。

图1分析：观察图形可知，DC＝AC－AD，根据已知的比例关系，AC、AD 均可用所求量 AB 表示，这样通过已知量 DC，即可求出 AB。

解：因为点 C 分线段 AB 为 5：7，点 D 分线段 AB 为 5：11所以又因为 CD＝10cm，所以 AB＝96cm例 2. 如图2，已知线段AB＝80cm，M 为AB 的中点，P 在MB 上，N 为PB 的中点，且NB＝14cm，求PA 的长。

图 2分析：从图形可以看出，线段 AP 等于线段 AM 与MP 的和，也等于线段 AB 与PB 的差，所以，欲求线段 PA 的长，只要能求出线段 AM 与MP 的长或者求出线段 PB 的长即可。

解：因为 N 是 PB 的中点，NB＝14所以 PB＝2NB＝2×14＝28又因为 AP＝AB－PB，AB＝80所以 AP＝80－28＝52（cm）说明：在几何计算中，要结合图形中已知线段和所求线段的位置关系求解，要做到步步有根据。

例 3. 如图3，一条直线上顺次有A、B、C、D 四点，且C 为AD 的中点，，求 BC 是 AB 的多少倍？图 3分析：题中已给出线段BC、AB、AD 的一个方程，又C 为AD 的中点，即，观察图形可知，，可得到BC、AB、AD 又一个方程，从而可用AD 分别表示AB、BC。

解：因为 C 为 AD 的中点，所以因为，即又由<1>、<2>可得：即 BC＝3AB例 4. 如图 4，C、D、E 将线段 AB 分成 2：3：4：5 四部分，M、P、Q、N 分别是AC、CD、DE、EB 的中点，且 MN＝21，求 PQ 的长。

期末复习专题08 线段与角有关动点的计算问题考点一 有关线段的中点计算问题考点二 有关角的平分线计算问题考点三 线段上动点计算问题 考点四 角上动点计算问题考点一 有关线段的中点计算问题故选：D ．【点睛】此题主要考查线段之间的关系，解题的关键是熟知线段的和差关系．2．（2022·新疆·乌鲁木齐八一中学七年级期中）如图，数轴上M ，N ，P ，Q 四点对应的数都是整数，且M 为线段NQ 的中点，P 为线段NM 的中点．若点M 对应的整数是a ，点N 对应的整数是b ，且20b a -=，则数轴上的原点是（ ）A ．点MB ．点NC ．点PD ．点Q【答案】D 【分析】由已知条件可知2QN QM =，因为点M 对应的整数是a ，点N 对应的整数是b ，且20b a -=，依此可得到数轴上的原点．【详解】解：∵点M 为线段NQ 的中点，∴2QN QM =，∵点M 对应的整数是a ，点N 对应的整数是b ，且20b a -=，∴数轴上的原点是Q ．故选：D ．【点睛】利用中点性质转化线段之间的倍分关系是解题的关键，在不同的情况下灵活选用它的不同表示方法，有利于解题的简洁性．同时，灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点．3．（2022·云南·楚雄市中山镇初级中学七年级期末）C 为直线AB 上一点，且线段3cm AB =，5cm =BC ，则AC 的长度是 ________．【答案】8cm 或2cm【分析】分A 、C 在点B 异侧和A 、C 在点B 同侧两种情况，分别作出图形，根据线段的和差计算即可．【详解】解：如图1，当A 、C 在点B 异侧时，358cm AC AB BC =+=+=，如图2，当点A 、C 在点B 同侧时，532cm AC BC AB =-=-=，即AC 的长度是8cm 或2cm ，故答案为：8cm 或2cm ．【点睛】本题考查了线段的和差计算，注意分类讨论思想的应用．4．（2022·全国·七年级专题练习）如图，M 是AB 的中点，N 是BC 的中点，7cm AB =，2cm BN =，则BC =________cm ，MC =______cm ．AB=，点C线段(1)如图，已知线段8cmQ 点M 是AC 中点，12MC AC \=，M Q 为AC 的中点，N 为BC 的中点，1CM AC \=，1CN BC =，(1)若点C 为图1中线段AB 的“优点”6()AC AC BC =<(2)若点D 也是图1中线段AB 的“优点”（不同于点C ）（填“=”或“¹”）[解决问题]∵点D是线段AB的“优点”，考点二有关角的平分线计算问题【点睛】本题主要考查了角平分线有关的计算以及几何图形中角的计算，解题关键是根据题意作出图形，运用分类讨论的思想分析问题．2．（2022·浙江台州·七年级期末）直线AB ，CD 相交于点O ，OE 是BOD Ð的角平分线，若3AOE BOC Ð=Ð，则EOC Ð的度数为( )A ．36°B ．72°C ．108°D ．144°【答案】C 【分析】根据OE 是BOD Ð的角平分线，得出DOE BOE Ð=Ð，根据3AOE AOD DOE BOC Ð=Ð+Ð=Ð，得出2DOE BOC Ð=Ð，求出36BOC Ð=°，即可得出272BOE BOC Ð=Ð=°，即可得出答案．【详解】解：∵OE 是BOD Ð的角平分线，∴DOE BOE Ð=Ð，∵3AOE AOD DOE BOC Ð=Ð+Ð=Ð，又∵AOD BOC Ð=Ð，∴3BOC DOE BOC Ð+Ð=Ð，∴2DOE BOC Ð=Ð，∴2BOE DOE BOC Ð=Ð=Ð，∵180DOE BOE BOC Ð+Ð+Ð=°，∴22180BOC BOC BOC Ð+Ð+Ð=°，解得：36BOC Ð=°，272BOE BOC \Ð=Ð=°，∴108EOC BOE BOC Ð=Ð+Ð=°，故C 正确．故选：C ．【点睛】本题主要考查了角平分线的定义，根据已知条件得出2DOE BOC Ð=Ð，是解题的关键．3．（2022·全国·七年级课时练习）如图，AB 、CD 交于点O ，若170=°∠，射线OE 平分∠AOC ，那么∠EOD =__________度．【答案】42°##42度【分析】先由对顶角相等求出【详解】解：∵∠AOC =∠∴∠BOD =70°，∵:2:3BOE EOD ÐÐ=，Ð，OD(1)如图1，OE平分AOB(2)如图2，OE、OD分别平分ÐÐ(3)若OE、OD分别平分AOC 接填空）．则EOD EOC Ð=Ð1122AOC =Ð-Ð1(2AOB BOC =Ð+Ð45=°；则1(2EOD AOC Ð=Ð1(360)2AOB °=-Ð1(36090)2°°=-(1)如图1，过点O 作射线OE ，使OE 为AOD Ð的角平分线，当Ð=COE (2)如图2，过点O 作射线OE ，当OE 恰好为AOC Ð的角平分线时，另作射线求EOF Ð的度数；(3)过点O 作射线OE ，当OC 恰好为AOE Ð的角平分线时，另作射线OF ，时，求BOD Ð的度数．考点三线段上动点计算问题考点四 角上动点计算问题1．（2022·河北·石家庄外国语学校七年级期中）如图，将直角三角板ABC 绕顶点A 顺时针旋转到AB C ¢V ，点B ¢恰好落在CA 的延长线上，60BAC Ð=°，90C Ð=°，则旋转角BAB Т为（ ）A ．60°B ．100°C ．120°D ．150°【答案】C 【分析】直接根据180BAB BAC ¢Ð=°-Ð即可得出答案．【详解】解：∵将直角三角板ABC 绕顶点A 顺时针旋转到AB C ¢V ，点B ¢恰好落在CA 的延长线上，60BAC Ð=°，∴180********BAB BAC ¢Ð=°-Ð=°-°=°，故选：C ．【点睛】本题考查了旋转角，题目比较简单，属于基础题．2．（2022·陕西·西安辅轮中学七年级期末）已知：O 是直线AB 上的一点，∠COD 是直角，OE 平分∠BOC ．Ð=°Q，POB68\Ð=°-°，68POM nÐ=°Q，MON90\Ð=°-°-°=°-°，1809090AON n n\Ð-Ð=°-°-°-°=°；AON POM n n(90)(68)22当6890<<时，如图2，理由如下：nQ，Ð=°68POB\Ð=°-°，POM n68Q，Ð=°90MON\Ð=°-°-°=°-°，AON n n1809090\Ð+Ð=°-°+°-°=°；(90)(68)22AON POM n n故答案为：068n<<，6890<<．n【点睛】本题主要考查角的加减运算，能够熟练根据要求列角的等量关系是解题关键．。

类比计算 轻松解题角和线段有很多类似的属性，因此在研究有关角的计算问题，常可通过类比线段问题予以轻松解决．现举例说明，供参考．一、有关等分计算问题例1 如图1，∠AOB 是直角，∠BOC 是锐角，OE 平分∠AOC ，OF 平分∠BOC ，求∠EOF 的度数．分析：由于角的图形比较复杂，要解决这个问题，可退而先求与其类似的有关线段等分计算问题“如图2，线段AB=8，C 点在线段AB 的延长线上，E 是线段AC 中点，F 是线段BC 中点，求线段EF 的长．”解决这个问题，显然要比解决上面角的问题简单．从图形可以看出，EF=EC －FC ，而E 是线段AC 中点，F 是线段BC 中点，所以EF=21AC －21BC=21( AC －BC)=21AB=4．类比此解法，可以求出∠EOF 的度数．解：因为∠EOF=∠EOC －∠FOC ，而OE 平分∠AOC ，OF 平分∠BOC ，所以∠EOF=21∠AOC －21∠BOC=21(∠AOC －∠BOC)=21∠AOB=45º． 二、有关和差计算问题例2 如图3，已知∠AOC=∠BOD=50º，∠BOC=20º，求∠AOD 的度数． 分析：图形比较复杂，类比“如图4，已知AC=BD=5，BC=2，求AD 的长．”由图4，显然有AC+BD=AB+BC+BC+CD=AD+BC ，所以AD=AC+BD －BC=5+5－2=8的度数．解：因为∠AOC+∠BOD=∠AOB+∠BOC+∠BOC+∠COD=∠AOD+∠COD，所以∠AOD=∠AOC+∠BOD－∠BOC=50º+50º－20º=80º．点评：从上面的解法可以看出，有很多角与线段的类似计算问题，我们可以通过类比，在解决线段问题的同时，也能顺利解决角的问题，由于线段相关的知识和图形比较简单，容易理解与掌握，因此对于图形比较复杂的角的计算问题，我们提倡大家利用类比推理的方法去进行研究，这样不但有助于理解新知识，还有利于创新意识的培养．。

线段与角度的测量与计算在几何学中，线段和角度是最基本的测量单位。

线段用来表示两点之间的距离，而角度用来度量物体之间的旋转程度。

掌握线段和角度的测量与计算方法对于解决各种几何问题至关重要。

本文将介绍线段和角度的测量方法，并提供一些相关计算的实例。

一、线段的测量方法线段的测量是指通过测量两点之间的直线距离来确定线段的长度。

测量线段的常用工具是直尺和卷尺。

测量线段的步骤如下：1. 将直尺或卷尺的一端与线段的起点对齐。

2. 沿着线段的方向，将直尺或卷尺延伸至线段的终点。

3. 读取直尺或卷尺上线段的长度。

需要注意的是，在测量线段时要确保测量工具与线段保持紧密接触，以避免测量误差的产生。

此外，对于曲线线段的测量，可以采用一些其他的测量方法，如利用软尺沿着曲线的轮廓测量。

线段的计算可以通过将线段与数轴对应起来进行。

数轴上每个刻度代表一个单位长度，将线段的起点和终点分别对应到数轴上的刻度上，然后读取两个刻度值的差即可得到线段的长度。

二、角度的测量方法角度的测量是指通过测量两条射线之间的夹角来确定角度的大小。

测量角度的常用工具是量角器和转角尺。

测量角度的步骤如下：1. 将量角器或转角尺的一个尺腿与角的顶点对齐。

2. 通过另一个尺腿与角的两条射线对齐，确保量角器或转角尺紧密贴合。

3. 读取量角器或转角尺上的角度数值。

需要注意的是，角度的测量应该尽量精确，尽量避免视觉误差带来的测量偏差。

此外，在测量尖锐角时，可以使用直角器来帮助确定直角，从而减小误差。

角度的计算可以通过以下方法进行。

首先，将角转化为圆周上的弧度表示，然后利用弧度值进行计算。

例如，一个180°的角对应了圆周的π弧度。

三、线段和角度的计算实例下面通过一些实例来演示线段和角度的计算方法：1. 示例一：已知线段AB的长度为5cm，线段BC的长度为3cm，求线段AC的长度。

根据线段的计算方法，线段AC的长度等于线段AB的长度加上线段BC的长度，即5cm + 3cm = 8cm。

线段的长度与角度在几何学中，线段的长度与角度是两个重要的概念。

线段是指两个点之间的直线部分，长度是描述线段的大小，而角度则是两条线段之间的夹角大小。

本文将从理论和实际应用的角度分别讨论线段长度与角度的相关性。

一、线段长度线段长度是指两个点之间的距离，可以用数值表示。

在平面几何学中，我们可以通过两点之间的坐标计算线段的长度。

假设有两个点A(x₁, y₁)和B(x₂, y₂)，则线段AB的长度可以通过以下公式计算：AB = √((x₂ - x₁)² + (y₂ - y₁)²)这个公式被称为勾股定理，也是线段长度的计算公式。

通过这个公式，我们可以得到线段的精确长度，无论线段是水平、垂直还是倾斜的。

线段长度的计算在实际中有广泛的应用。

例如，在建筑设计中，需要计算建筑物的各个模块的尺寸，包括线段的长度。

在工程测量中，也常常需要测量线段的长度来确定地块的大小或测绘地形图。

线段长度的准确计算对于这些应用非常重要。

二、线段角度线段的角度是指两个线段之间的夹角大小。

角度可以用弧度或度数来表示。

在平面几何学中，我们通常使用度数来表示角度。

360度是一个完整的圆，而角度的单位可以是任意的。

例如，直角是90度，平分一个直角则是45度。

要计算线段的角度，我们需要明确两个线段之间关系的性质和角度的计算方法。

例如，两条直线相交时，相交处形成的角度叫做相交角。

相交角的计算可以使用数学中的三角函数。

通过三角函数的计算，我们可以得到线段之间的夹角大小。

线段角度的计算在实际中也有广泛的应用。

例如，在导航系统中，我们需要知道两条线段之间的角度，以确定行驶方向或路径选择。

在机器人技术中，精确计算线段角度可以帮助机器人进行路径规划和避障。

总结：线段的长度与角度是几何学中重要的概念。

线段长度可以通过勾股定理计算，而线段角度可以通过三角函数计算。

线段长度与角度的准确计算在实际应用中有广泛的应用，包括建筑设计、工程测量、导航系统和机器人技术等领域。

线段和角的基本概念及其计算线段和角是几何学中的基本概念，对于几何学的学习和应用具有重要意义。

线段是由两个端点确定的有限直线段，而角是由两个射线共享一个端点而形成的图形。

在本文中，将介绍线段和角的基本概念，并探讨如何进行相关计算。

一、线段的基本概念线段是指由两个端点和着连结两个端点的直线所组成的有限部分。

线段可以用字母和横线表示，例如AB表示一条由点A和点B连接的线段。

线段的长度可以通过测量直线上的两个端点之间的距离来获得。

长度的测量单位可以是厘米、米等。

计算线段长度的方法是使用坐标系下的距离公式，根据两点的坐标计算两点之间的距离。

二、角的基本概念角是由两个射线共享一个端点而形成的图形。

共享的端点称为角的顶点，而两个射线则是角的边。

角可以用大写字母表示，例如∠ABC表示由射线AB和射线BC所形成的一个角。

角可以分为几类：锐角、直角、钝角和平角。

锐角是小于90°的角，直角是等于90°的角，钝角是大于90°但小于180°的角，平角是等于180°的角。

三、线段的计算1. 线段的加法线段的加法是指将两个线段连接起来形成一个更长的线段的操作。

这可以通过线段的端点进行连接而实现。

例如，给定线段AB和线段BC，我们可以通过将A和C连接来得到更长的线段AC。

2. 线段的减法线段的减法是指将一个线段从另一个线段中减去的操作。

这可以通过线段的端点来实现。

例如，给定线段AC和线段BC，我们可以通过从AC中减去BC来得到线段AB。

3. 线段的乘法线段的乘法是指将一个线段的长度与一个数进行乘法运算的操作。

例如，给定线段AB，如果要将其长度扩大2倍，可以将线段的长度乘以2。

四、角的计算1. 角的加法角的加法是指将两个角连接起来形成一个更大的角的操作。

这可以通过角的顶点和边进行连接而实现。

例如，给定∠ABC和∠BCD，我们可以通过将射线AB和射线CD连接来得到更大的角∠ABD。

平面几何中的线段与角度计算在平面几何学中，线段和角度是两个基本的概念。

线段是一个有两个端点的直线部分，它可以通过测量长度来确定。

而角度是由两条交叉的线段形成的空间区域，用于描述物体之间的方位关系。

在本文中，我们将讨论线段的计算和测量，以及角度的计算方法。

一、线段的计算和测量方法1. 直尺法直尺法是一种常用的线段计算和测量方法。

首先，我们需要一把直尺，将其边与线段的一端对齐，然后沿着直尺的边缘延伸，直到达到线段的另一端。

通过读取直尺上的刻度，我们可以得到线段的长度。

2. 钢尺法钢尺法也是一种常用的线段计算和测量方法。

与直尺法类似，我们需要一把刻有刻度的钢尺。

将钢尺的一端对齐线段的一端，然后延伸钢尺直到达到线段的另一端。

通过读取钢尺上的刻度，我们可以得到线段的长度。

相比直尺法，钢尺法的精度更高。

3. 割线法割线法是一种通过几何原理计算线段长度的方法。

首先，我们需要一块刻有刻度的长直板。

将直板上的一条边与线段的一端对齐，并用手指按住与线段相切的另一条边。

然后，将直板沿着手指的位置移动，直到与线段的另一端相切。

通过读取直板上的刻度，我们可以得到线段的长度。

二、角度的计算方法1. 量角器法量角器是一种用于测量和计算角度的工具。

将量角器的一个端点对齐于角的顶点，然后将量角器的另一条边与角的一条边对齐。

通过读取量角器上的刻度，我们可以得到角的度数。

2. 三角函数法三角函数是一种用于计算角度的数学工具。

在平面几何中，常用的三角函数有正弦、余弦和正切等。

通过使用三角函数的定义和性质，我们可以计算某些特定角度的值。

3. 直观估计法在某些情况下，我们可以通过直观估计的方式得到角度的近似值。

例如，对于钝角或锐角，我们可以根据视觉判断来估计其大致值。

这种方法通常用于大致的角度计算，不适用于精确的测量。

结论通过直尺法、钢尺法和割线法，我们可以计算和测量线段的长度。

而借助量角器法、三角函数法和直观估计法，我们可以计算角度的大小。