回归分析之分类变量的编码方法
- 格式:ppt
- 大小:1.70 MB
- 文档页数:26

回归分析是统计学中一种常见的数据分析方法,用于研究一个或多个自变量与因变量之间的关系。
在实际应用中,回归分析经常需要对变量进行转换,以满足模型的假设或改善模型的拟合效果。
本文将讨论回归分析中的变量转换技巧,包括对连续变量和分类变量的转换方法以及常见的应用场景。
**连续变量的转换**在回归分析中,连续变量是指可以在一定范围内取任意值的变量,例如年龄、收入等。
对于连续变量,常见的转换方法包括取对数、平方、开方等。
首先,对数转换是常用的一种方法。
当自变量或因变量的分布偏态严重时,取对数可以使数据更加符合正态分布,从而满足回归模型的假设。
例如,当因变量呈现指数增长的趋势时,可以对其取对数,使之线性化。
另外,对数转换还可以减少极端值的影响,提高模型的稳健性。
其次,平方和开方转换也是常见的方法。
当因变量和自变量之间存在非线性关系时,通过平方或开方转换可以使其线性化。
例如,当研究身高和体重之间的关系时,可以考虑对身高进行平方转换,以捕捉体重随身高变化的非线性趋势。
此外,还有其他一些转换方法,如倒数转换、指数转换等,可以根据具体情况选择合适的方法。
需要注意的是,转换后的变量需要与原始变量具有一定程度的线性关系,同时要避免过度转换导致模型失真。
**分类变量的转换**除了连续变量,回归分析中还常常涉及分类变量。
分类变量是指具有有限个取值的变量,例如性别、学历等。
对于分类变量,常见的转换方法包括虚拟变量编码、因子变量编码等。
首先,虚拟变量编码是最常用的方法之一。
虚拟变量编码将原始的分类变量转换为多个二元变量,用0和1表示。
例如,对于性别这一分类变量,可以通过虚拟变量编码将其转换为一个“男”变量和一个“女”变量,分别表示是否为男性和女性。
虚拟变量编码可以使分类变量在回归分析中更好地参与建模,同时避免了将分类变量视为连续变量的问题。
其次,因子变量编码是另一种常见的转换方法。
因子变量编码将原始的分类变量转换为数值型的因子变量,以便在回归分析中使用。

回归分析是统计学中一种重要的分析方法,它用来研究自变量和因变量之间的关系。
在进行回归分析时,有时候需要对变量进行转换,以满足回归分析的前提条件或者改善模型的性能。
在这篇文章中,我将从常见的变量转换技巧入手,探讨回归分析中的变量转换技巧。
1. 自然对数转换自然对数转换是回归分析中常见的一种变量转换方法。
在实际数据分析中,很多变量的分布会呈现偏态分布或者右偏斜的特点,这时候可以考虑对自变量或者因变量进行自然对数转换。
自然对数转换可以将偏态分布的数据变换为近似正态分布,有助于提高模型的拟合效果和预测准确性。
2. 平方根转换平方根转换是另一种常见的变量转换方法。
当变量的分布呈现左偏斜或者右偏斜时,可以考虑对变量进行平方根转换。
平方根转换可以降低变量的偏度和峰度,使得变量更加接近正态分布,有利于改善模型的性能。
3. 反正弦转换反正弦转换是一种特殊的变量转换方法,它常用于处理百分比或比率等变量。
在回归分析中,有时候需要研究百分比或比率与因变量之间的关系,这时候可以考虑对百分比或比率进行反正弦转换。
反正弦转换可以将百分比或比率转换为角度,使得变量更加符合正态分布,有助于改善回归模型的拟合效果。
4. Box-Cox转换Box-Cox转换是一种广义的变量转换方法,它可以对各种类型的变量进行转换,包括正态分布、偏态分布和右偏斜分布等。
Box-Cox转换通过引入参数λ,对变量进行不同程度的幂次转换,使得变量更加接近正态分布。
Box-Cox转换可以根据数据的实际情况选择合适的参数λ,是一种非常灵活和有效的变量转换方法。
5. 分类变量的虚拟变量转换在回归分析中,经常会遇到分类变量(如性别、地区、学历等)的处理问题。
对于分类变量,常见的处理方法是引入虚拟变量。
虚拟变量转换可以将分类变量转换为二进制的0和1,以便于在回归模型中进行分析。
虚拟变量转换是回归分析中必不可少的一种技巧,可以有效地处理分类变量对模型的影响。
6. 离散化变量的分组转换除了连续变量的转换,回归分析中还需要处理离散化变量的转换。

二元logistic回归分析1.理论Logistic回归模型:设因变量为Y,自变量为x1,x2,...,xn。
事件发生与不发生的概率比Pi /(1-pi)被称为事件发生比。
后对事件发生比做对数变换,能得到logistic回归的线性模式:ln(pi /(1-pi))=β+β1x1+...βnxn采用最大似然比法或者迭代法对参数的估计,参数通过似然比检验和Wold 检验。
二元logistic回归是指因变量为二分类变量时的回归分析。
在建立回归模型时,目标的取值范围在0-1之间。
常因变量为二分类数据自变量可以是连续型随机变量和分类数据图1数据类型2.重新编码操作步骤首先将数据导入spss中,数据情况如下图所示,首先先对变量进行重新编码处理。
图2数据情况第一步、点击转换、重新编码为相同的变量。
图3数据编码第一步第二步:进入图中变量框后,将需要处理的变量放入变量放入框中,后点击旧值和新值,在旧值中输入原有值,后在新值中输入新值,点击添加、继续。
图4数据编码第二步3.二元logistic回归分析操作步骤第一步:点击分析、回归、二元logistic。
图5二元logistic回归分析第一步第二步:进入图中对话框后将因变量、自变量放入对应变量框中,点击分类、进入定义分类变量框后。
将协变量框中的分类变量放入分类协变量框中(一般情况除二分类或有序分类数据不需哑变量设置),并进行哑变量的设置,点击继续。
图6第二步第三步:点击选项,勾选霍斯默-莱梅肖拟合优度、Exp(B)的置信区间、迭代历史记录。
点击继续、确定。
图7选项勾选4.二元logistic回归分析结果二元logistic回归分析的个案摘要、因变量编码、分类变量编码结果。
图8分类变量编码迭代历史记录、分类表、方程中的变量、未包括在方程中的变量结果。
图9块0:起始块迭代历史记录、模型中的Omnibus检验、模型摘要、霍斯默-莱梅肖检验。
图10块1:方法=输入分类表、方差中的变量结果。

在MATLAB中进行分类和回归分析在科学和工程领域,分类和回归分析是常见的数据分析方法。
而MATLAB作为一种功能强大的数据分析软件,提供了丰富的工具和函数,使得分类和回归分析变得更加简单和高效。
本文将介绍在MATLAB中进行分类和回归分析的方法和技巧,帮助读者更好地理解和应用这些技术。
一、背景介绍分类和回归分析是基于已知数据的模式进行预测和分类的统计方法。
分类分析用于将数据分为不同的类别,而回归分析则试图通过已知数据的模式预测未知数据的数值。
这些方法在各个领域都有广泛的应用,如金融、医疗、市场营销等。
二、数据准备在进行分类和回归分析之前,需要准备好相应的数据。
一般来说,数据应当包含自变量(也称为特征或输入)和因变量(也称为标签或输出)。
自变量是用来作为预测或分类的输入变量,而因变量是要预测或分类的目标变量。
通常情况下,数据应当是数值型的,如果包含分类变量,需要进行相应的编码或处理。
三、分类分析在MATLAB中进行分类分析,有多种方法和技术可供选择。
其中最常见的方法包括K最近邻算法(K-nearest neighbors)和支持向量机(Support Vector Machines)等。
这些方法都有相应的函数,可以用于在MATLAB中实现分类分析。
K最近邻算法基于训练样本和测试样本之间的距离,将测试样本分类为与其最近的K个训练样本所属的类别。
而支持向量机则试图找到一个超平面,将不同类别的样本分开,并使得分类误差最小化。
在MATLAB中,我们可以使用fitcknn和fitcsvm函数来实现K最近邻算法和支持向量机。
除了上述方法,还有其他的分类算法可以在MATLAB中使用,如决策树、随机森林等。
根据数据的具体情况和需求,选择适合的分类算法非常重要。
四、回归分析在进行回归分析时,我们需要首先选择适当的回归模型。
常用的回归模型包括线性回归、多项式回归、岭回归等。
根据数据的分布和特点,选择合适的回归模型能够提高分析的准确性。
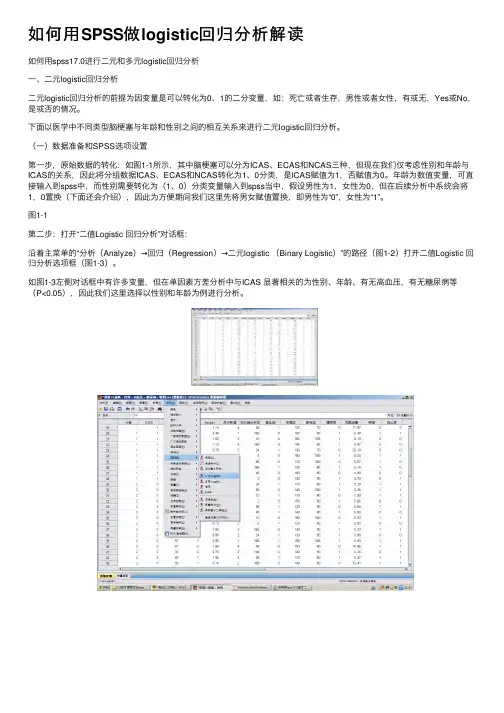
如何⽤SPSS做logistic回归分析解读如何⽤spss17.0进⾏⼆元和多元logistic回归分析⼀、⼆元logistic回归分析⼆元logistic回归分析的前提为因变量是可以转化为0、1的⼆分变量,如:死亡或者⽣存,男性或者⼥性,有或⽆,Yes或No,是或否的情况。
下⾯以医学中不同类型脑梗塞与年龄和性别之间的相互关系来进⾏⼆元logistic回归分析。
(⼀)数据准备和SPSS选项设置第⼀步,原始数据的转化:如图1-1所⽰,其中脑梗塞可以分为ICAS、ECAS和NCAS三种,但现在我们仅考虑性别和年龄与ICAS的关系,因此将分组数据ICAS、ECAS和NCAS转化为1、0分类,是ICAS赋值为1,否赋值为0。
年龄为数值变量,可直接输⼊到spss中,⽽性别需要转化为(1、0)分类变量输⼊到spss当中,假设男性为1,⼥性为0,但在后续分析中系统会将1,0置换(下⾯还会介绍),因此为⽅便期间我们这⾥先将男⼥赋值置换,即男性为“0”,⼥性为“1”。
图1-1第⼆步:打开“⼆值Logistic 回归分析”对话框:沿着主菜单的“分析(Analyze)→回归(Regression)→⼆元logistic (Binary Logistic)”的路径(图1-2)打开⼆值Logistic 回归分析选项框(图1-3)。
如图1-3左侧对话框中有许多变量,但在单因素⽅差分析中与ICAS 显著相关的为性别、年龄、有⽆⾼⾎压,有⽆糖尿病等(P<0.05),因此我们这⾥选择以性别和年龄为例进⾏分析。
在图1-3中,因为我们要分析性别和年龄与ICAS的相关程度,因此将ICAS选⼊因变量(Dependent)中,⽽将性别和年龄选⼊协变量(Covariates)框中,在协变量下⽅的“⽅法(Method)”⼀栏中,共有七个选项。
采⽤第⼀种⽅法,即系统默认的强迫回归⽅法(进⼊“Enter”)。
接下来我们将对分类(Categorical),保存(Save),选项(Options)按照如图1-4、1-5、1-6中所⽰进⾏设置。

在回归分析中,自变量可以是连续的(数值型)或离散的(类别型)。
类别变量是一种离散变量,通常用于表示分类数据,例如性别(男/女)、国籍(中国/美国/其他)、婚姻状态(已婚/未婚)等。
当我们处理类别变量时,线性回归方程可能不适用,因为类别变量是非数值型的。
然而,我们可以使用逻辑回归(Logistic Regression)来处理类别变量。
逻辑回归是一种用于预测二分类因变量的统计方法。
它的基本思想是通过一个逻辑函数将自变量与因变量连接起来,然后使用最大似然估计法估计参数。
逻辑回归的数学模型如下:
P(Y=1) = 1 / (1 + exp(-(β0 + β1X1 + β2X2 + ... + βnXn)))
其中:
•P(Y=1) 是因变量为1的概率
•β0, β1, β2, ..., βn 是模型的参数
•X1, X2, ..., Xn 是自变量
•exp() 是自然指数函数
在Python中,可以使用sklearn库中的LogisticRegression类来拟合逻辑回归模型。
以下是一个简单的示例:
需要注意的是,逻辑回归假设因变量是二分类的,且自变量和因变量之间的关系是线性关系。
如果这些假设不成立,可能需要使用其他方法来处理类别变量。

stata 分类变量回归在Stata中,进行分类变量回归可以通过使用回归分析的命令来实现。
在回归模型中,分类变量通常需要进行虚拟变量编码,也称为哑变量编码,以便将其纳入回归模型中。
以下是在Stata中进行分类变量回归的一般步骤:1. 创建虚拟变量:首先,你需要将分类变量转换为虚拟变量。
在Stata中,你可以使用命令 "tabulate" 来查看分类变量的不同取值,并使用 "tabulate" 命令后面加上 "generate" 选项来生成虚拟变量。
例如,如果你的分类变量是 "group",你可以使用以下命令来生成虚拟变量:tabulate group, generate(group_dummy)。
2. 运行回归分析:一旦生成了虚拟变量,你可以将这些变量与其他自变量一起纳入回归模型中。
使用 "regress" 命令可以进行最小二乘回归分析。
例如,如果你的因变量是 "y",自变量包括连续变量 "x" 和虚拟变量 "group_dummy1" 和 "group_dummy2",你可以使用以下命令进行回归分析:regress y x group_dummy1 group_dummy2。
3. 解释结果,在得到回归结果后,你需要解释虚拟变量的系数。
系数表示了每个虚拟变量对因变量的影响。
通常,虚拟变量的系数表示了该变量相对于参照组的影响。
此外,在Stata中还有其他一些用于处理分类变量的命令,如"xi" 命令用于创建虚拟变量,以及 "tabulate" 命令用于查看分类变量的分布情况。
在进行分类变量回归时,还需要考虑模型的适配性、残差分析等问题,以确保回归模型的有效性和准确性。
总之,通过以上步骤,你可以在Stata中进行分类变量回归分析,并得到相应的回归结果和解释。

逻辑回归类别变量和连续变量的交互对分类变量的解释-概述说明以及解释1.引言1.1 概述在统计学和机器学习领域中,逻辑回归是一种常用的分类算法。
它可以用来预测二分类问题,并且广泛应用于各种领域,包括医疗、金融、市场营销等。
然而,在实际应用中,我们经常会遇到同时包含类别变量和连续变量的数据集。
这就引发了一个问题:类别变量和连续变量之间是否存在某种交互作用,对逻辑回归模型的分类结果是否有影响?本文将探讨类别变量和连续变量之间的交互作用,并研究其对逻辑回归模型的解释能力的影响。
我们将详细介绍逻辑回归的原理和算法,并分析交互作用对分类变量解释能力的影响。
通过实证研究和数据分析,我们将提供一些有关如何处理类别变量和连续变量交互的实用技巧和建议。
文章的结构如下:引言部分将对逻辑回归、类别变量和连续变量进行简要介绍,并明确文章的目的。
接着,在正文部分,我们将详细讨论类别变量和连续变量的交互作用,并介绍如何解释逻辑回归模型中的分类变量。
最后,在结论部分,我们总结了本文的主要内容,并探讨了研究结果的意义。
通过本文的阅读,读者将了解到类别变量和连续变量的交互作用对逻辑回归模型的影响,并可以在实际应用中更准确地解释和使用逻辑回归模型。
此外,本文的研究结果还具有一定的理论和实践意义,对相关领域的学术研究和实际工作具有一定的参考价值。
1.2文章结构文章结构部分的内容可以包括以下信息:在本篇论文中,将探讨逻辑回归模型中类别变量和连续变量的交互对分类变量的解释的影响。
首先,将介绍逻辑回归模型和其在分类问题中的应用。
逻辑回归模型是一种常用的统计学习方法,广泛应用于二元分类问题。
它使用逻辑函数来建模分类变量,通过最大似然估计方法来估计模型的参数,从而预测分类结果。
然后,将详细讨论类别变量和连续变量的交互对逻辑回归模型的影响。
在实际问题中,常常会遇到一些特征既包括类别变量又包括连续变量的情况。
类别变量表示不同类别之间的差异,而连续变量表示数值上的差异。


stata分类变量哑变量cox回归在Stata中进行Cox回归分析时,如果自变量是分类变量(也称为哑变量或虚拟变量),需要进行哑变量编码。
下面是一些基本步骤:创建哑变量: 首先,你需要为分类变量创建哑变量。
例如,假设你有一个名为"race"的分类变量,它有3个类别:white, black, and other。
你可以使用tabulate命令创建哑变量:statatabulate race, generate(race_1)tabulate race, generate(race_2)tabulate race, generate(race_3)这将会生成3个哑变量race_1、race_2和race_3,分别代表"white"、"black"和"other"。
2. 进行Cox回归: 接下来,你可以使用coxph命令进行Cox回归分析。
在模型中包含所有生成的哑变量。
例如:statacoxph y x1 x2 (race_1=x3 race_2=x4 race_3=x5), robust这里,y是你的生存时间或事件指示器,x1、x2等是你的其他自变量,x3、x4、x5等是你的哑变量的协变量。
3. 解释结果: 在结果中,每个哑变量的系数表示相对于参考类(通常是第一个类别)的相对风险。
例如,如果"black"的系数是0.5,那么相对于"white","black"的相对风险是0.5。
4. 注意事项: 在创建哑变量时,请确保每个类别都有一个哑变量,并且将参考类别(通常是第一个类别)的哑变量设置为0。
此外,对于具有很多类别的分类变量,创建哑变量可能会导致模型过于复杂和解释性差。
在这种情况下,可以考虑使用其他方法,如限制比例风险模型或混合效应模型。
这些步骤可以帮助你在Stata中进行Cox回归分析时处理分类变量。
第8 章利用SPSS 进行Logistic 回归分析现实中的很多现象可以划分为两种可能,或者归结为两种状态,这两种状态分别用0和1 表示。
如果我们采用多个因素对0-1 表示的某种现象进行因果关系解释,就可能应用到logistic 回归。
Logistic 回归分为二值logistic 回归和多值logistic 回归两类。
首先用实例讲述二值logistic 回归,然后进一步说明多值logistic 回归。
在阅读这部分内容之前,最好先看看有关SPSS 软件操作技术的教科书。
§8.1 二值logistic 回归8.1.1 数据准备和选项设置我们研究2005 年影响中国各地区城市化水平的经济地理因素。
城市化水平用城镇人口比重表征,影响因素包括人均GDP、第二产业产值比重、第三产业产值比重以及地理位置。
地理位置为名义变量,中国各地区被分别划分到三大地带:东部地带、中部地带和西部地带。
我们用各地区的地带分类代表地理位置。
第一步:整理原始数据。
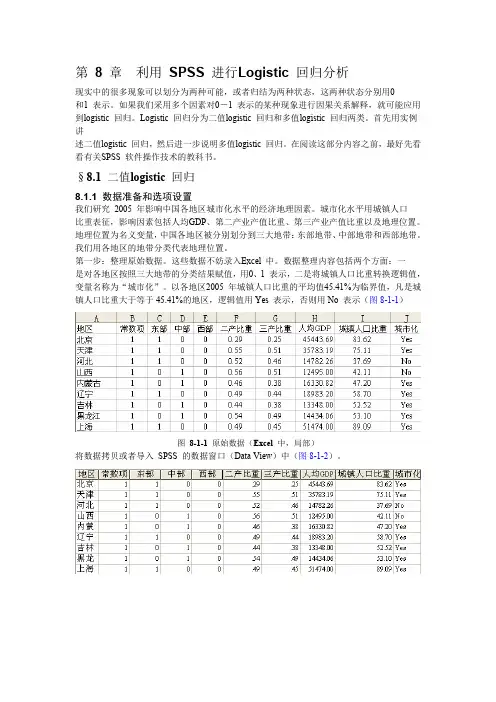
这些数据不妨录入Excel 中。
数据整理内容包括两个方面:一是对各地区按照三大地带的分类结果赋值,用0、1 表示,二是将城镇人口比重转换逻辑值,变量名称为“城市化”。
以各地区2005 年城镇人口比重的平均值45.41%为临界值,凡是城镇人口比重大于等于45.41%的地区,逻辑值用Yes 表示,否则用No 表示(图8-1-1)图8-1-1 原始数据(Excel 中,局部)将数据拷贝或者导入SPSS 的数据窗口(Data View)中(图8-1-2)。
图8-1-2 中国31 个地区的数据(SPSS 中,局部)第二步:打开“聚类分析”对话框。
沿着主菜单的“Analyze→Regression→Binary Logistic K”的路径(图8-1-3)打开二值Logistic 回归分析选项框(图8-1-4)。
图8-1-3 打开二值Logistic 回归分析对话框的路径对数据进行多次拟合试验,结果表明,像二产比重、三产比重等对城市化水平影响不显著。
逻辑回归分类变量
逻辑回归是一种用于处理分类问题的统计学习方法。
在逻辑回归中,我们通常使用分类变量作为自变量来预测因变量的取值。
分类变量是一种用于对个体进行分类或分组的变量,它的取值通常是离散的,代表不同的类别或水平。
在逻辑回归中,分类变量通常被编码为虚拟变量或哑变量。
这意味着如果分类变量有k个水平,我们需要创建k-1个虚拟变量来表示这个分类变量。
这是为了避免虚拟变量陷阱,即多重共线性的问题。
例如,如果我们有一个性别变量,它有两个水平,男和女。
我们会创建一个虚拟变量来表示性别,比如用1表示男性,0表示女性。
在逻辑回归中,我们使用分类变量的虚拟变量作为自变量来拟合一个逻辑函数,从而预测因变量的概率。
逻辑回归的目标是找到最佳的参数估计,使得逻辑函数能够最好地拟合观测数据,从而对未知数据进行分类预测。
除了使用虚拟变量表示分类变量外,我们还可以对分类变量进行特征工程,例如进行分箱处理、标签编码或独热编码等,以便更
好地应用于逻辑回归模型中。
总的来说,逻辑回归是一种处理分类变量的有效方法,通过合
理的编码和特征工程,可以很好地应用于分类问题的预测和建模中。
希望这个回答能够全面回答你的问题。
一、回归分析的分类logistic回归(logistic regression)是研究因变量为二分类或多分类观察结果与影响因素(自变量)之间关系的一种多变量分析方法,属概率型非线性回归。
根据1个因变量与多个因变量之分,有以下区分:①一个因变量y:I连续形因变量(y)——线性回归分析II分类型因变量(y)——Logistic 回归分析III 生存时间因变量(y)——生存风险回归分析IV时间序列因变量(y)——时间序列分析②多个因变量(y1,y2,……yn):I 路径分析II 结构方程模型分析在流行病学研究中,常需要分析疾病与各种危险因素间的定量关系,同时为了能真实反映暴露因素与观察结果间的关系,需要控制混杂因素的影响。
(1)Mantel-Haenszel分层分析:适用于样本量大、分析因素较少的情况。
当分层较多时,由于要求各格子中例数不能太少,所需样本较大,往往难以做到;当混杂因素较多时,分层数也呈几何倍数增长,这将导致部分层中某个格子的频数为零,无法利用其信息。
(2)线性回归分析:由于因变量是分类变量,不能满足其正态性要求;有些自变量对因变量的影响并非线性。
(3)logistic回归:不仅适用于病因学分析,也可用于其他方面的研究,研究某个二分类(或无序及有序多分类)目标变量与有关因素的关系。
二、logistic回归分析(一)logistic回归的分类(1)二分类资料logistic回归:因变量为两分类变量的资料,可用非条件logistic回归和条件logistic回归进行分析。
非条件logistic回归多用于非配比病例-对照研究或队列研究资料,条件logistic回归多用于配对或配比资料。
(2)多分类资料logistic回归:因变量为多项分类的资料,可用多项分类logistic回归模型或有序分类logistic回归模型进行分析。
队列研究(cohort study):也称前瞻性研究、随访研究等。
是一种由因及果的研究,在研究开始时,根据以往有无暴露经历,将研究人群分为暴露人群和非暴露人群,在一定时期内,随访观察和比较两组人群的发病率或死亡率。
r语言二元logistic回归多分类变量处理R语言是一种强大的统计分析工具,具有丰富的统计函数和可视化功能。
在数据分析领域,二元logistic回归是一种常用的统计方法,用于预测二分类变量的概率。
然而,当面对多分类变量时,我们就需要对数据进行特殊处理。
本文将就R语言中二元logistic回归多分类变量的处理进行探讨,并深入分析其原理和应用。
1. 了解多分类变量在数据分析中,我们经常会遇到需要对多个类别进行分类的情况。
在市场调查中,我们可能需要根据消费者的芳龄、性别和收入水平等多个因素对其进行分类。
这就涉及到了多分类变量的处理。
在R语言中,我们需要对多分类变量进行特殊的处理,才能在二元logistic回归中进行准确的分析和预测。
2. R语言中多分类变量处理的方法在R语言中,我们可以使用one-hot编码(One-Hot Encoding)来处理多分类变量。
这是一种将多分类变量转换为虚拟变量的方法,从而使得每个类别都拥有自己的二元变量。
通过这种方法,我们能够将多分类变量转化为适合二元logistic回归分析的形式。
3. 实例分析举个例子来说明多分类变量的处理方法。
假设我们有一个数据集,其中包含了消费者的芳龄、性别和收入水平等多个变量,我们需要对他们进行分类。
我们需要对多分类变量进行one-hot编码,将每个类别转化为二元变量。
我们可以利用二元logistic回归模型来进行分析和预测。
4. 个人观点在实际的数据分析工作中,我发现对多分类变量的处理十分重要。
合理的处理方法能够提高模型的准确性和可解释性。
在R语言中,使用one-hot编码是一种简单而有效的处理多分类变量的方法。
通过这种方法,我们可以更好地利用二元logistic回归模型进行数据分析。
总结在本文中,我们针对R语言中二元logistic回归多分类变量的处理进行了深入探讨。
通过对多分类变量的处理方法进行分析和实例说明,我相信读者已经对这一方法有了更深入的理解。
如何用spss17.0进行二元和多元logis tic回归分析一、二元logis tic回归分析二元logis tic回归分析的前提为因变量是可以转化为0、1的二分变量,如:死亡或者生存,男性或者女性,有或无,Yes或No,是或否的情况。
下面以医学中不同类型脑梗塞与年龄和性别之间的相互关系来进行二元logist ic回归分析。
(一)数据准备和SP SS选项设置第一步,原始数据的转化:如图1-1所示,其中脑梗塞可以分为ICAS、ECAS和NC AS三种,但现在我们仅考虑性别和年龄与ICAS的关系,因此将分组数据ICAS、ECAS和NC AS转化为1、0分类,是ICAS赋值为1,否赋值为0。
年龄为数值变量,可直接输入到s pss中,而性别需要转化为(1、0)分类变量输入到spss当中,假设男性为1,女性为0,但在后续分析中系统会将1,0置换(下面还会介绍),因此为方便期间我们这里先将男女赋值置换,即男性为“0”,女性为“1”。
图1-1第二步:打开“二值Logis tic 回归分析”对话框:沿着主菜单的“分析(Analyze)→回归(Regress ion)→二元logis tic (BinaryLogisti c)”的路径(图1-2)打开二值Log istic回归分析选项框(图1-3)。
如图1-3左侧对话框中有许多变量,但在单因素方差分析中与IC AS 显著相关的为性别、年龄、有无高血压,有无糖尿病等(P<0.05),因此我们这里选择以性别和年龄为例进行分析。
在图1-3中,因为我们要分析性别和年龄与ICAS的相关程度,因此将ICAS选入因变量(Depende nt)中,而将性别和年龄选入协变量(Covaria tes)框中,在协变量下方的“方法(Method)”一栏中,共有七个选项。
逻辑回归的变量类型的处理方法-概述说明以及解释1.引言1.1 概述逻辑回归是一种常用的分类算法,可以用于预测二分类问题。
在应用逻辑回归之前,针对不同类型的变量,我们需要对其进行处理,以确保模型的准确性和可靠性。
本文将详细介绍逻辑回归中变量类型的处理方法。
在进行逻辑回归之前,我们首先需要了解不同变量类型的分类。
变量可以分为两大类:连续变量和离散变量。
连续变量是在一个范围内有无限多个可能值的变量,例如年龄、身高等。
而离散变量则是只有有限个可能值的变量,例如性别、学历等。
针对连续变量,我们通常采取的处理方法是进行归一化或者标准化。
归一化可以将变量的取值范围缩放到0-1之间,而标准化则是将变量的取值转化为均值为0,标准差为1的正态分布。
通过这些处理方法,可以消除不同变量之间的量纲差异,使得模型更加准确。
对于离散变量,我们可以采用编码的方式进行处理。
常见的编码方法有哑变量编码和标签编码。
哑变量编码将原始的离散变量转化为多个二进制变量,用于表示每个可能取值的存在与否。
而标签编码则是将每个取值映射为一个数字。
通过这些编码方法,可以将离散变量转化为模型可以处理的数值。
在本文的接下来的部分,我们将详细介绍连续变量和离散变量的处理方法,并给出具体的示例和实践经验。
同时,我们也会讨论处理不平衡数据和缺失值的相关策略,以提高模型的准确性和稳定性。
总的来说,逻辑回归的变量类型的处理方法对于建立准确可靠的模型至关重要。
通过合理的处理方法,我们可以充分利用各个变量的信息,提高模型的预测能力,为实际问题的解决提供有力的支持。
在接下来的章节中,我们将一一介绍并深入讨论这些处理方法及其应用。
1.2文章结构文章结构部分的内容编写如下:1.2 文章结构本文主要围绕逻辑回归的变量类型展开讨论,在以下章节中将详细介绍不同变量类型的处理方法。
首先,我们将在第2.1节对变量类型进行分类,包括连续变量和离散变量。
随后,在第2.2节中,我们将重点介绍连续变量的处理方法,包括数据标准化、离群值处理和多项式特征构造等。