第九章 属性(分类)数据分析
- 格式:ppt
- 大小:354.00 KB
- 文档页数:46


第9章 分类数据分析一、思考题1.简述列联表的构造与列联表的分布。
答:列联表是由两个以上的变量进行交叉分类的频数分布表。
列联表的分布可以从两个方面看,一个是观察值的分布,又称为条件分布,每个具体的观察值就是条件频数;一个是期望值的分布。
2.用一张报纸、一份杂志或你周围的例子构造一个列联表,说明这个调查中两个分类变量的关系,并提出进行检验的问题。
答:对三个生产厂甲、乙、丙提供的学习机的A、B、C三种性能进行质量检验,欲了解生产厂家同学习机性能的质量差异是否有关系。
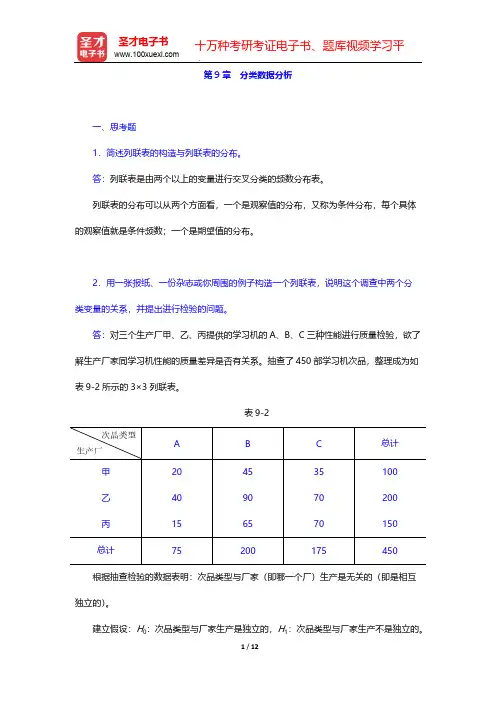
抽查了450部学习机次品,整理成为如表9-2所示的3×3列联表。
表9-2根据抽查检验的数据表明:次品类型与厂家(即哪一个厂)生产是无关的(即是相互独立的)。
建立假设:H0:次品类型与厂家生产是独立的,H1:次品类型与厂家生产不是独立的。
可以计算各组的期望值,如表9-3所示(表中括号内的数值为期望值)。
表9-3 各组的期望值计算表所以2222(2017)(4033)(7058)9.821173358χ---=+++=…。
而自由度等于(R -1)(C -1)=(3-1)×(3-1)=4,若以0.01的显著性水平进行检验,查χ2分布表得20.01(4)13.277χ=。
由于220.019.821(4)13.277χχ=<=,故接受原假设H 0,即次品类型与厂家生产是独立的。
3.说明计算2χ统计量的步骤。
答:计算2χ统计量的步骤:(1)用观察值o f 减去期望值e f ;(2)将(o f -e f )之差平方;(3)将平方结果2)(e o f f -除以e f ;(4)将步骤(3)的结果加总,即得:22()o e ef f f χ-=∑。
4.简述ϕ系数、c 系数、V 系数的各自特点。
答:(1)ϕ相关系数是描述2×2列联表数据相关程度最常用的一种相关系数。
它的计算公式为:ϕ,式中,∑-=ee of f f 22)(χ;n 为列联表中的总频数,也即样本量。



![第九章 属性(分类)数据分析[最新]](https://uimg.taocdn.com/dc8db13010a6f524ccbf8595.webp)



第05讲第九章统计与成对数据的统计分析(综合测试)第05讲第九章统计与成对数据的统计分析(综合测试)一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)(2022·全国·高一课时练习)1.“中国天眼”为500米口径球面射电望远镜,是具有我国自主知识产权、世界最大单口径、最灵敏的射电望远镜.建造“中国天眼”的目的是()A .通过调查获取数据B .通过试验获取数据C .通过观察获取数据D .通过查询获得数据(2022·黑龙江·大庆市东风中学高一期末)2.嫦娥五号的成功发射,实现了中国航天史上的五个“首次”,某中学为此举行了“讲好航天故事”演讲比赛.若将报名的30位同学编号为01,02,…,30,利用下面的随机数表来决定他们的出场顺序,选取方法是从随机数表第1行的第3列和第4列数字开始由左到右依次选取两个数字,重复的跳过,则选出来的第5个个体的编号为()4567321212310201045215200112512932049234493582003623486969387481A .23B .20C .15D .12(2022·全国·高一单元测试)3.电影《长津湖之水门桥》于2022年2月1日上映.某新闻机构想了解市民对《长津湖之水门桥》的评价,决定从某市3个区按人口数用分层随机抽样的方法抽取一个样本.若3个区人口数之比为2:3:5,且人口最多的一个区抽出了100人,则这个样本的容量为().A .100B .160C .200D .240(2022·重庆·高二阶段练习)4.下表是某饮料专卖店一天卖出奶茶的杯数y 与当天气温x (单位:C )的对比表,已知表中数据计算得到y 关于x 的线性回归方程为ˆˆ27ybx =+,则据此模型预计35C 时卖出奶茶的杯数为()气温/Cx 510152025杯数y2620161414A .4B .5C .6D .7(2022·福建·莆田一中高二期末)5.某高中调查学生对2022年冬奥会的关注是否与性别有关,随机抽样调查150人,进行独立性检验,经计算得()()()()()22 5.879n ad bc a b c d a c b d χ-=≈++++,临界值表如下:α0.150.100.050.0250.010x α2.0722.0763.8415.0246.635则下列说法中正确的是:()A .有97.5%的把握认为“学生对2022年冬奥会的关注与性别无关”B .有99%的把握认为“学生对2022年冬奥会的关注与性别有关”C .在犯错误的概率不超过2.5%的前提下可认为“学生对2022年冬奥会的关注与性别有关”D .在犯错误的概率不超过2.5%的前提下可认为“学生对2022年冬奥会的关注与性别无关”(2022·广西河池·高二期末(文))6.一只红铃虫的产卵数y 和温度x 有关,现收集了6组观测数据,y (单位:个)与温度x (单位:℃)得到样本数据(),i i x y (1i =,2,3,4,5,6),令ln i i z y =,并将(),i i x z 绘制成如图所示的散点图.若用方程e bx y a =对y 与x 的关系进行拟合,则()A .1a >,0b >B .1a >,0b <C .01a <<,0b >D .01a <<,0b <(2022·全国·高一单元测试)7.2022年国务院《政府工作报告》中指出,有序推进碳达峰碳中和工作,落实碳达峰行动方案.汽车行业是碳排放量比较大的行业之一,某检测单位对甲、乙两类MI 型品牌的新车各抽取了5辆进行2CO 排放量检测,记录如下(单位:g/km ),则甲、乙两品牌汽车2CO 的排放量稳定性更好的是()甲80110120140150乙100120100120160A .甲B .乙C .甲、乙相同D .无法确定(2022·全国·高一单元测试)8.期末考试后,高二某班50名学生物理成绩的平均分为85,方差为8.2,则下列四个数中不可能是该班物理成绩的是()A .60B .78C .85D .100二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)(2022·福建南平·高一期末)9.关于用统计方法获取数据,分析数据,下列结论正确的是()A .某食品加工企业为了解生产的产品是否合格,合理的调查方式为抽样调查B .为了解高一学生的视力情况,现有高一男生480人,女生420人,按性别进行分层抽样,样本量按比例分配,若从女生中抽取的样本量为63,则样本容量为135C .若甲、乙两组数据的标准差满足<甲乙s s ,则可以估计乙比甲更稳定D .若数据123,,,,n x x x x ⋅⋅⋅的平均数为x ,则数据(1,2,3,,)i i y ax b i n =-=⋅⋅⋅的平均数为ax b-(2022·全国·高一单元测试)10.下图是甲、乙两个工厂的轮胎宽度的雷达图(虚线代表甲,实线代表乙).根据图中的信息,下列说法正确的是()A .甲厂轮胎宽度的平均数大于乙厂轮胎宽度的平均数B .甲厂轮胎宽度的众数大于乙厂轮胎宽度的众数C .甲厂轮胎宽度的中位数与乙厂轮胎宽度的中位数相同D .甲厂轮胎宽度的极差小于乙厂轮胎宽度的极差(2022·云南省下关第一中学高三开学考试)11.自2020年初,新型冠状病毒引起的肺炎疫情爆发以来,各地医疗机构采取了各种有针对性的治疗方法,取得了不错的成效,某地开始使用中西医结合方法后,每周治愈的患者人数如表所示,由表格可得y 关于x 的二次回归方程为2ˆ6yx a =+,则下列说法正确的是()周数(x )12345治愈人数(y )2173693142A .4a =B .8a =-C .此回归模型第4周的残差(实际值与预报值之差)为5D .估计第6周治愈人数为220(2022·广东汕头·高二期末)12.已知由样本数据()(),1,2,3,,10i i x y i = 组成的一个样本,得到回归直线方程为20.4y x =-,且2x =,去除两个歧义点()2,1-和()2,1-后,得到新的回归直线的斜率为3.则下列说法正确的是()A .相关变量x ,y 具有正相关关系B .去除两个歧义点后的回归直线方程为 33y x =-C .去除两个歧义点后,样本(4,8.9)的残差为0.1-D .去除两个歧义点后,随x 值增加相关变量y 值增加速度变小三、填空题:(本题共4小题,每小题5分,共20分,其中第16题第一空2分,第二空3分.)(2022·陕西渭南·高一期末)13.已知某种商品的广告费支出x (单位:万元)与销售额y (单位:万元)之间有如下对应数据:x 24568y3040506070根据上表可得线性回归方程ˆ7ˆyx a =+,据此估计,当投入15万元广告费时,销售额为_______万元.(2022·重庆十八中高二期末)14.某篮球联赛期间,某一电视台对年龄高于30岁和不高于30岁的人是否喜欢甲队进行调查,对高于30岁的调查了45人,不高于30岁的调查了55人,所得数据绘制成如下列联表:年龄是否喜欢甲队合计不喜欢甲队喜欢甲队高于30岁pq45不高于30岁154055合计15p +40q +100若工作人员从调查的所有人中任取一人,取到喜欢甲队的人的概率为35,依据小概率值0.005α=的独立性检验,推断年龄与是否喜欢甲队______(填“有”“无”)关联.附:()()()()()22n ad bc K a b c d a c b d -=++++,n a b c d =+++.α0.0500.0100.0050.0012K 3.8416.6357.87910.828(2022·福建厦门·高一期末)15.某电池厂有A ,B 两条生产线制造同一型号可充电电池.现采用样本量比例分配的分层随机抽样,从某天两条生产线上的成品中随机抽取样本,并测量产品可充电次数的均值及方差,结果如下:项目抽取成品数样本均值样本方差A 生产线产品82104B 生产线产品122004则20个产品组成的总样本的方差为_____.(2022·天津津衡高级中学有限公司高三阶段练习)16.对正在横行全球的“新冠病毒”,某科研团队研发了一款新药用于治疗,为检验药效,该团队从“新冠”感染者中随机抽取若干名患者,检测发现其中感染了“普通型毒株”、“奥密克戎型毒株”、“其他型毒株”的人数占比为5:3:2.对他们进行治疗后,统计出该药对“普通型毒株”、“奥密克戎毒株”、“其他型毒株”的有效率分别为78%、60%、75%,那么你预估这款新药对“新冠病毒”的总体有效率是________;若已知这款新药对“新冠病毒”有效,求该药对“奥密克戎毒株”的有效率是________.四、解答题(本题共6小题,共70分,其中第17题10分,其它每题12分,解答应写出文字说明、证明过程或演算步骤.)(2022·全国·高一课时练习)17.某工厂对200个电子元件的使用寿命进行检查,按照使用寿命(单位:h )可以把这批电子元件分成六组.由于工作中不慎将部分数据丢失,现有以下部分图表:分组[)100,200[)200,300[)300,400[)400,500[)500,600[]600,700频数3020频率0.20.4(1)求图2中A 的值;(2)补全图2频率分布直方图,并求图2中阴影部分的面积;(3)为了某次展销会,用分层抽样的方法在寿命位于[)400,600内的产品中抽取5个作为样本,那么在[)400,500内应抽取多少个?(2022·全国·高一单元测试)18.在①样本容量为190,②抽取的高一学生人数为36这两个条件中任选一个,补充在下面问题中,并解答问题.某校为了解学生课外阅读情况,将每周阅读时间超过10小时的学生称为“阅读者”,在“阅读者”中按年级用分层随机抽样的方法抽取部分学生进行问卷调查.已知该校高一、高二、高三的学生人数和“阅读者”情况分别如图(1)和图(2)所示,且______.(1)求抽取的“阅读者”中高三学生的人数;(2)为了深入了解高三学生阅读情况,利用随机数表法抽取样本时,先对被抽取的高三“阅读者”按01,02,03,…进行编号,然后从随机数表第8行第5列的数字开始从左向右读,依次抽取5个编号,写出被选出的5个学生的编号.(注:如下为随机数表的第8行至第11行)630163785916955947199850717512867358332112342978645607825207443815510013注:如果选择多个条件分别解答,按第一个解答计分.(2022·河南信阳·高二期末(文))19.随着人们生活水平的提高,国家倡导绿色安全消费,菜篮子工程从数量保障型转向质量效益型.为了测试甲、乙两种不同有机肥料的使用效果,某科研单位用西红柿做了对比实验,分别在两片实验区各摘取100个,对其质量的某项指标值进行检测,质量指数值达到35及以上的为“质量优等”,由测量结果绘成如下频率分布直方图,其中质量指数值分组区间是:[)20,25,[)25,30,[)30,35,[)35,40,[]40,45.(1)分别求甲片实验区西红柿的质量指数的平均值和中位数,并从统计学的角度说明平均值、中位数哪一个更能代表甲片实验区西红柿的质量指数;(2)请根据题中信息完成下面的列联表,并判断是否有99.9%的把握认为“质量优等”与使用不同的肥料有关;甲有机肥料乙有机肥料合计质量优等质量非优等合计()()()()()22n ad bc x a b c d a c b d -=++++.()20P x x ≥0.1000.0500.0100.0050.0010x 2.7063.8416.6357.87910.828(2022·陕西·宝鸡市金台区教育体育局教研室高二期末(理))20.如图是某采矿厂的污水排放量(y 单位:吨)与矿产品年产量(x 单位:吨)的折线图:(1)依据折线图计算相关系数(r 精确到0.01),并据此判断是否可用线性回归模型拟合y 与x 的关系?(若||0.75r >,则线性相关程度很高,可用线性回归模型拟合)(2)若可用线性回归模型拟合y 与x 的关系,请建立y 关于x 的线性回归方程,并预测年产量为10吨时的污水排放量.相关公式:()(niix x yy r --∑0.95≈≈.回归方程ˆˆˆybx a =+中,121()()ˆˆˆ,.()niii nii x x y y b a y bxx x ==--==--∑∑(2022·全国·高一单元测试)21.2022年“中国航天日”线上启动仪式在4月24日上午举行,为普及航天知识,某校开展了“航天知识竞赛”活动,现从参加该竞赛的学生中随机抽取了60名,统计他们的成绩(满分100分),其中成绩不低于80分的学生被评为“航天达人”,将数据整理后绘制成如图所示的频率分布直方图.(1)若该中学参加这次竞赛的共有2000名学生,试估计全校这次竞赛中“航天达人”的人数;(2)估计参加这次竞赛的学生成绩的80%分位数;(3)若在抽取的60名学生中,利用分层随机抽样的方法从成绩不低于70分的学生中随机抽取6人,则从成绩在[70,80),[80,90),[90,100]内的学生中分别抽取了多少人?(2022·宁夏·石嘴山市第三中学模拟预测(文))22.新型冠状病毒肺炎COVID-19疫情发生以来,在世界各地逐渐蔓延.在全国人民的共同努力和各级部门的严格管控下,我国的疫情已经得到了很好的控制.然而,小王同学发现,每个国家在疫情发生的初期,由于认识不足和措施不到位,感染人数都会出现快速的增长.下表是小王同学记录的某国连续8天每日新型冠状病毒感染确诊的累计人数.日期代码x 12345678累计确诊人数y481631517197122为了分析该国累计感染人数的变化趋势,小王同学分别用两杆模型:①2ˆybx a =+,②ˆydx c =+对变量x 和y 的关系进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差e ˆi ii y y =- ):经过计算得81()()728i i i x x y y =--=∑,821()42i i x x =-=∑,81()()6868i i i z z y y =--=∑,821(3570i i z z =-=∑,其中2i iz x =,8118i i z z ==∑.(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由;(2)根据(1)问选定的模型求出相应的回归方程(系数均保留两位小数);(3)由于时差,该国截止第9天新型冠状病毒感染确诊的累计人数尚未公布.小王同学认为,如果防疫形势没有得到明显改善,在数据公布之前可以根据他在(2)问求出的回归方程来对感染人数做出预测,那么估计该地区第9天新型冠状病毒感染确诊的累计人数是多少?(结果保留整数)附:回归直线的斜率和截距的最小二乘估计公式分别为:()()()81821ˆiii ii x x y y bx x ==--=-∑∑,ˆˆay bx =-.参考答案:1.C【分析】直接由获取数据的途径求解即可.【详解】“中国天眼”主要是通过观察获取数据.故选:C .2.C【分析】根据随机数表法的概念直接得解.【详解】根据随机数表法可得选出的个体编号依次为:12,02,01,04,15,第5个个体编号为15,故选:C.3.C【分析】根据分层抽样的抽取比例相同求解即可.【详解】解:由3个区人口数之比为2:3:5,得第三个区所抽取的人数最多,所占比例为50%.又因为此区抽取了100人,所以3个区所抽取的总人数为100÷50%=200,即这个样本的容量为200.故选:C .4.C【分析】先求得ˆb的值,再据此模型计算出35C 时卖出奶茶的杯数.【详解】由题可知1(510152025)155x =++++=,1(2620161414)185y =++++=,由ˆ181527b=+,可得3ˆ5b =-,则3ˆ352765y=-⨯+=则据此模型预计35C 时卖出奶茶的杯数为6.故选:C 5.C【分析】根据独立性检验的方法即可求解.【详解】由题意可知,()()()()()22 5.879 5.024n ad bc a b c d a c b d χ-=≈>++++,所以在犯错误的概率不超过2.5%的前提下可认为“学生对2022年冬奥会的关注与性别有关”.故选:C.6.A【分析】令ln z y =,可得z 与x 的回归方程为ln z bx a =+,根据散点图,可得z 与x 正相关,所以0b >,根据纵截距大于0,可得a 的范围,即可得答案.【详解】因为e bx y a =,令ln z y =,则z 与x 的回归方程为ln z bx a =+.根据散点图可知z 与x 正相关,所以0b >.由回归直线图象可知:回归直线的纵截距大于0,即ln 0a >,所以1a >,故选:A.7.B【分析】分别计算甲类、乙类品牌汽车的2CO 排放量的平均值和方差即可求出答案.【详解】甲类品牌汽车的2CO 排放量的平均值80110120140150120(g/km)5x ++++==甲,甲类品牌汽车的2CO ,排放量的方差2222221[(80120)(110120)(120120)(140120)(150120)]6005s =⨯-+-+-+-+-=甲.乙类品牌汽车的2CO 排放量的平均值100120100120160120(g/km)5x ++++==乙,乙类品牌汽车的2CO 排放量的方差22221[(100120)(120120)(100120)5s =⨯-+-+-+乙22(120120)(160120)]480-+-=,所以22乙甲<s s .故选:B.8.A【分析】利用方差的定义、计算公式进行判断.【详解】根据题意,平均数85x =,方差()502211858.250i i s x ==-=∑,所以()5021858.250410ii x =-=⨯=∑,若存在60x =,则()26085625410-=>,则方差必然大于8.2,不符合题意,所以60不可能是所有成绩中的一个数据.又()2788549410-=<,()285850410-=<,()210085225410-=<.故B ,C ,D 错误.故选:A .9.ABD【分析】根据普查的适用情形即可判断A,根据分层抽样的抽样比即可求解B,根据标准差的含义即可判断C ,根据平均数的性质即可判断D.【详解】对于A:了解生产的产品是否合格,合理的调查方式为抽样调查,故A 正确;对于B,根据分层抽样的抽样比可知样本容量为()63480420=135420⨯+,故B 对对于C:因为<甲乙s s ,所以甲的数据更稳定,故C 错误,对于D:根据平均数的性质:(1,2,3,,)i i y ax b i n =-=⋅⋅⋅的平均数为ax b -,故D 对故选:ABD 10.ACD【分析】根据雷达图逐项判断可得答案.【详解】甲厂轮胎宽度分别为194,194,194,195,196,197,乙厂轮胎宽度分别为191,193,194,195,195,196,甲厂轮胎宽度平均数为19431951961971956⨯+++=,乙厂轮胎宽度平均数为19521911931941961946⨯++++=,195194>,故A 正确;甲厂轮胎宽度的众数是194,乙厂轮胎宽度的众数是195,195194>,故B 错误;甲厂轮胎宽度的中位数为195194194.52+=,乙厂轮胎宽度的中位数为195194194.52+=,故C 正确;甲厂轮胎宽度的极差为1971943-=,乙厂轮胎宽度极差为1961915-=,53>,故D 正确.故选:ACD .11.BC【分析】设2t x =,则ˆ6yt a =+,求出样本中心点即可判断选项A,B ;利用残差公式计算判断选项C ;令6x =,计算即可判断选项D.【详解】解:设2t x =,则ˆ6yt a =+,由已知得11(1491625)11,(2173693142)5855t y =++++==++++=所以586118a =-⨯=-,故选项A 错误,选项B 正确;在2ˆ68yx =-中,令4x =,得24ˆ64888y =⨯-=,所以此回归模型第4周的残差44ˆ93885y y=-=-=.故选项C 正确;在2ˆ68yx =-中,令6x =,得26ˆ668208y =⨯-=,故选项D 错误.故选:BC .12.ABC【分析】回归直线方程的斜率大小可以判断A 和D ;残差为真实值与估计值之差,进而判断C ;根据题意算出新的相关变量的平均值,进一步求出 a,进而判断B.【详解】对A ,因为回归直线的斜率大于0,即相关变量x ,y 具有正相关关系,故A 正确;对B ,将2x =代入 20.4y x =-得 3.6y =,则去掉两个歧义点后,得到新的相关变量的平均值分别为2105 3.6109,Y 8282X ⨯⨯====, 953322a=-⨯=-,此时的回归直线方程为 33y x =-,故B 正确;对C ,x =4时, 343=9y =⨯-,残差为8.9-9=-0.1,故C 正确;对D ,斜率3>1,此时随x 值增加相关变量y 值增加速度变大,D 错误.故选:ABC.13.120【分析】根据表中数据求得样本中心(),x y ,代入回归方程y bx a =+$$$后求得 a,然后再求当15x =的函数值即可.【详解】由上表可知:2456830405060705,5055x y ++++++++====.得样本点的中心为()5,50,代入回归方程y bx a =+$$$,得507515a =-⨯=$.所以回归方程为 715y x =+,将15x =代入可得:120y =$.故答案为:12014.有【分析】先根据条件列方程组求出p 、q ,然后计算2K 查表可知.【详解】由题知403100545q p q +⎧=⎪⎨⎪+=⎩,解得20,25q p ==所以()221002540152024508.2497.87940604555297K ⨯-⨯==>⨯⨯⨯所以有99.5%的把握认为年龄与是否喜欢甲队有关.故答案为:有15.28【分析】利用均值公式计算出总样本的均值,再利用方差的公式:22211n ii S x x n ==-∑,求出21nii x=∑,进一步求出总样本的方差即可.【详解】依题意得,82221121048Ai i S x ==-=∑,1222211200412B i i S x ==-=∑,解得:()822184210i i x ==⨯+∑,()12221124200ii x==⨯+∑,又8128210122002042020A B x x x +⨯+⨯=== ,()()20812222221112221120420201842101242002042028.i i i i i i S x x x x ===⎛⎫∴=-=⨯+- ⎪⎝⎭⎡⎤=⨯⨯++⨯+-⎣⎦=∑∑∑∴20个产品组成的总样本的方差为28.故答案为:28.16.72%##182525%##14【分析】依据统计数据的平均数求法即可求得这款新药对“新冠病毒”的总体有效率;依据条件概率即可求得已知这款新药对“新冠病毒”有效条件下该药对“奥密克戎毒株”的有效率.【详解】(1)53278%60%75%72%101010⨯+⨯+⨯=(2)360%1025%72%⨯=故答案为:72%;25%17.(1)0.001A =(2)频率分布直方图见解析,阴影部分的面积为0.5(3)4个【分析】(1)根据频率除以组距等于A ,结合图中的数据求解即可,(2)根据频率分布表中的数据可补全频率分布上直方图,阴影部分的面积等于第4组和第5组的频率和,(3)利用分层抽样的定义求解.(1)由题意可知0.1100A =⨯,所以0.001A =.(2)补全后的频率分布直方图如图所示,阴影部分的面积为0.0041000.0011000.5⨯+⨯=.(3)由分层抽样的性质,知在[)400,500内应抽取0.4540.40.1⨯=+(个).18.(1)条件选择见解析,高三学生的人数为90(2)依次选出的编号是63,78,59,16,47【分析】(1)首先确定分层随机抽样的抽样比,再利用“阅读者”中高三学生的人数乘以抽样比即可.(2)利用随机数表法的规则依次取数即可.【详解】(1)由题图知,该校“阅读者”中,高一、高二、高三学生人数分别为180010%180⨯=,160020%320⨯=,150030%450⨯=.选①,因为样本容量为190,所以抽取的“阅读者”中高三学生的人数为45019090180320450⨯=++.选②,因为抽取的高一学生人数为36,所以抽取的“阅读者”中高三学生的人数为3645090180⨯=.(2)根据题意,从随机数表第8行第5列的数字开始从左向右读,依次选出的编号是63,78,59,16,47.19.(1)平均值为34.5,中位数为35.91,中位数更能代表甲片实验区西红柿的质量指数;(2)表格见解析,有99.9%的把握认为,“质量优等”与使用不同的肥料有关【分析】(1)根据频率分布直方图计算平均数即可,中位数是通过排序得到的,不受极端值的影响,故从统计学的角度中位数更能代表甲片实验区西红柿的质量指数.(2)根据频率分布直方图,补全列联表,计算2x ,即可得出结论.(1)解:甲片实验区西红柿的质量指数的平均值为22.50.0527.50.1532.50.237.50.5542.50.0534.5⨯+⨯+⨯+⨯+⨯=,设甲片实验区西红柿的质量指数的中位数为x ,则0.050.150.2(35)0.110.5x +++-⨯=,所以35.91x ≈,故甲片实验区西红柿的质量指数的中位数为35.91,从统计学的角度中位数更能代表甲片实验区西红柿的质量指数.(2)由题意可得22⨯列联表为甲有机肥料乙有机肥料合计质量优等603090质量非优等4070110合计100100200,()()()()()222200(42001200)18.18210010011090x a b n ad c d a c b d bc -⨯-=++=≈⨯⨯⨯++,因为()210.8280.001P x ≥≈,所以有99.9%的把握认为,“质量优等”与使用不同的肥料有关.20.(1)相关系数0.95,可用线性回归模型拟合y 与x 的关系(2)ˆ0.3 2.5yx =+,5.5吨【分析】(1)代入数据,算出相关系数r ,将其绝对值与0.75比较,即可判断可用线性回归模型拟合y 与x 的关系.(2)先求出回归方程,求出当10x =时的值,即为预测值.【详解】(1)由折线图得如下数据计算得:5x =,4y =,51()()6i i i x x y y =--=∑,552211()20,()2i i i i x x y y ==-=-=∑∑所以相关系数0.95r =≈,因为||0.75r >,所以可用线性回归模型拟合y 与x 的关系(2)6ˆ0.3,20b==40.352ˆˆ.5ay bx =-=-⨯=,所以回归方程为ˆ0.3 2.5yx =+,当10x =时,ˆ 5.5y=,所以预测年产量为10吨时的污水排放量为5.5吨21.(1)600人;(2)85;(3)3人,2人,1人.【分析】(1)根据频率分布直方图可求成绩在[80,100]内的频率,从而可求“航天达人”的人数.(2)根据频率和可确定成绩的80%分位数在[80,90)内,根据公式可求80%分位数;(3)根据成绩在[70,80),[80,90),[90,100]的频率比值可求各自抽取人数.【详解】(1)由频率分布直方图可知,成绩在[80,100]内的频率为0.020×10+0.010×10=0.3,则估计全校这次竞赛中“航天达人”的人数约为2000×0.3=600人.(2)由频率分布直方图可知,成绩在[40,50)内的频率为0.005×10=0.05,成绩在[50,60)内的频率为0.015×10=0.15,成绩在[60,70)内的频率为0.020×10=0.2,成绩在[70,80)内的频率为0.030×10=0.3,成绩在[80,90)内的频率为0.020×10=0.2,所以成绩在80分以下的学生所占的比例为70%,成绩在90分以下的学生所占的比例为90%,所以成绩的80%分位数一定在[80,90)内,而0.80.78010805850.90.7-+⨯=+=-,因此估计参加这次竞赛的学生成绩的80%分位数约为85.(3)因为0.3630.30.20.1⨯=++,0.2620.30.20.1⨯=++,0.1610.30.20.1⨯=++,所以从成绩在[70,80),[80,90),[90,100]内的学生中分别抽取了3人,2人,1人.22.(1)选择模型①,理由见解析(2)2ˆ 1.92 1.04yx =+(3)157【分析】(1)选择模型①.根据残差的意义直接判断;(2)套公式求出系数,即可得到y 关于x 的回归方程;(3)将9x =代入,即可求得.【详解】(1)选择模型①.理由如下:根据残差图可以看出,模型①的估计值和真实值相对比较接近,模型②的残差相对较大一些,所以模型①的拟合效果相对较好(2)由(1),知y 关于x 的回归方程为2ˆybx a =+,令2z x =,则ˆy bz a =+.由所给数据得:1(1491625364964)25.58z =+++++++=,1(481631517197122)508y =+++++++=,8121()()6868ˆ 1.923570()iii nii z z y y b z z ==--==≈-∑∑.ˆˆ50 1.9225.5 1.04ay bz =-≈-⨯=,∴y 关于x 的回归方程为2ˆ 1.92 1.04y x =+,(3)将9x =代入上式,得2ˆ 1.929 1.04156.56157y=⨯+=≈(人),所以预测该地区第9天新型冠状病毒感染确诊的累计人数为157人.。
