平面与圆柱面,圆锥面的截面

常见几何体的截面
常见几何体的截面通常指的是用一个平面截取几何体后与几何体相交得到的平面图形。

在立体几何中，截面问题是一个常见的题型，它要求我们理解和想象三维几何体被切割后的样子。

以下是一些常见几何体及其可能的截面形状：
1. 圆柱体：当用一个平面去截一个圆柱体时，如果截面平行于底面，那么截面形状是一个圆形；如果截面垂直于底面，那么截面形状是一个矩形。

2. 圆锥体：圆锥体的截面可能是圆形、椭圆形或者是抛物线形，这取决于截面的角度和位置。

如果截面平行于圆锥的底面，那么截面是一个小圆形；如果截面是斜截圆锥，那么截面可能是椭圆形或者抛物线形。

3. 球体：球体的截面总是圆形，不论截面的角度和位置如何，因为球体在任何方向上都是对称的。

4. 立方体：立方体的截面可能是正方形或长方形，这取决于截面的方向。

如果截面平行于立方体的一个面，那么截面是一个正方形；如果截面与立方体的一个面成一定角度，那么截面是一个长方形。

总的来说，了解这些常见几何体的截面形状对于解决立体几何问题非常有帮助，尤其是在处理高考或数学竞赛中的综合题目时。

圆锥曲线的原理最详细图解(平面与圆锥面的截线)本文介绍了平面与圆锥面的截线问题。

首先观察到平面截圆锥面的图形，可以得到三种圆锥曲线：椭圆、抛物线和双曲线。

然后讨论了一条直线与等腰三角形的位置关系，将等腰三角形拓广为圆锥，直线拓广为平面，通过定理得出了平面与圆锥的交线类型与夹角的关系。

接着利用Dandelin双球证明了椭圆的情况，并讨论了抛物线和双曲线的情况。

最后通过制作三维图形，展示了三种曲线的丹迪林Dandelin双球图。

6.在图中选取点O1和F1，以点O1为圆心作圆O1（在光照后会显示为球），以同样的方法作出圆O2.然后在线段EF上选取点G和H，以线段GDO的垂线上的伸缩点I为基准点，作出点I关于点G的对称点I’。

通过向量GH将点I和点I’平分，得到点I2和点I"。

将这些点连接起来，形成一个截面，其长和宽可以由点G、H和I控制，而点F则控制其旋转。

8.添加点J在下底圆上，然后将点OJ与截面相交于点K。

选取点J和K，形成一个轨迹，即截线，它在图中呈现为一个椭圆。

9.将点E按照向量OD'的方向平移，得到点E'。

将线段EE'与圆相交于点G1，使得线段EG1与母线OD'平行。

添加一个名为“抛物线”的动画，它将点F移动到点G1上。

10.参照前面的图形，添加其他的图形元素。

下载图霸文件后，在“对象浏览器”中查看各个对象。

课件下载：共享文件下载中心相关文章：1.利用丹迪林Dandelin双球证明平面与圆锥面的截线定理；2.平面与圆柱面的截线。

更多文章：《几何图霸》文章列表。

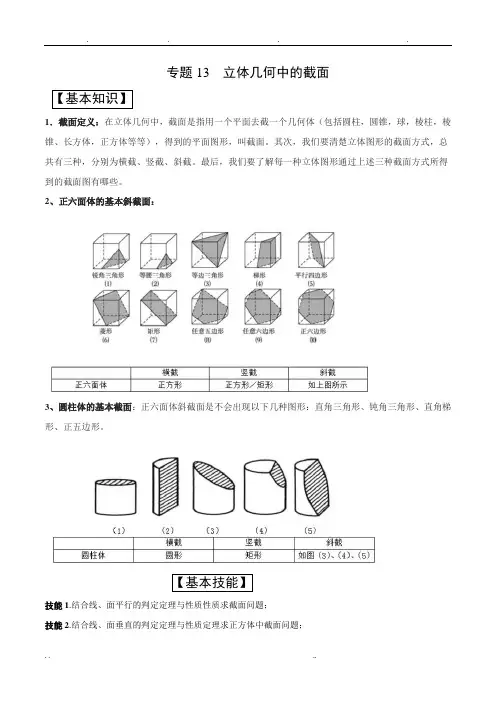
专题13 立体几何中的截面【基本知识】1．截面定义：在立体几何中，截面是指用一个平面去截一个几何体（包括圆柱，圆锥，球，棱柱，棱锥、长方体，正方体等等），得到的平面图形，叫截面。

其次，我们要清楚立体图形的截面方式，总共有三种，分别为横截、竖截、斜截。

最后，我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。

2、正六面体的基本斜截面：3、圆柱体的基本截面：正六面体斜截面是不会出现以下几种图形：直角三角形、钝角三角形、直角梯形、正五边形。

【基本技能】技能1.结合线、面平行的判定定理与性质性质求截面问题；技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题；技能3.猜想法求最值问题：要灵活运用一些特殊图形与几何体的特征，“动中找静”：如正三角形、正六边形、正三棱锥等；技能4.建立函数模型求最值问题：①设元②建立二次函数模型③求最值。

例1 一个正方体接于一个球，过这个球的球心作一平面，则截面图形不可能．．．是（ ）分析 考虑过球心的平面在转动过中，平面在球的接正方体上截得的截面不可能是大圆的接正方形，故选D 。

例2 如图，在透明的塑料制成的长方体ABCD-A 1B 1C 1D 1容器灌进一些水，固定容器底面一边BC 于地面上，再将容器倾斜，随着倾斜程度的不同，有下列四个命题：① 水的部分始终呈棱柱状； ② 水面EFGH 的面积不改变； ③ 棱A 1D 1始终与水面EFGH 平行；④ 当容器倾斜到如图5（2）时，BE·BF 是定值； 其中正确的命题序号是______________分析 当长方体容器绕BC 边转动时，盛水部分的几何体始终满足棱柱定义，故①正确；在转动过程中EH//FG ，但EH 与FG 的距离EF 在变，所以水面EFGH 的面积在改变，故②错误；在转动过程中，始终有BC//FG//A 1D 1，所以A 1D 1//面EFGH ，③正确；当容器转动到水部分呈直三棱柱时如图5（2），因为BC BF BE V ⋅⋅=21水是定值，又BC 是定值，所以BE·BF 是定值，即④正确。

平面与圆柱面的截交线形状
圆柱面和平面的截交线形状很复杂，有多种类型。

其中最简单的是一条直线，它沿着圆柱的底面的直径方向穿过圆柱的中心，也通过平面的中心，而这条直线的形状和长度完全取决于两个形状之间的参数。

其次，圆柱面和平面也可以有一个大圆弧，这个圆弧是由圆柱面的底面及平面组成的一部分，一个孤立的弧形被称为截面角，它可以从原点延伸到圆柱底部，然后再从这个圆柱底部伸出一个圆弧到平面，这样就可以得到一个完整的圆弧截交线，长度和角度完全由圆柱面和平面的参数和位置决定。

此外，圆柱面和平面的截交线形状还可能是一个圆形，如果当圆柱面的面积大于该平面时，圆柱面的圆柱可以完全穿过平面的中心，形成一个完整的圆，或者圆柱面的长度或宽度和平面的大小一样，而且圆柱两侧的圆可以完全切割过平面，形成一个完美的圆形截交线。

最后，圆柱面或者平面上有一系列曲线，如按照不同的长度和角度加入圆柱面，那么圆柱面和平面之间会形成一系列曲线状截交线，这些曲线状线均由圆柱面和平面之间的参数和位置决定，长度和角度也会不同，这样就可以形成复杂的形状。

总之，圆柱面和平面的截交线形状有多种多样，它们的形状完全
取决于两个形状之间的参数和位置，而其中最简单的是一条直线,以及大圆弧，圆形以及多种曲线状。

圆柱和圆锥的截面是什么图形我们知道，圆柱和圆锥中垂直于轴的横截面是一个圆面，那么截面不垂直于轴时又会是什么图形呢？关于这个问题，历史上许多人都做过卓有成效的研究，为了便于大家学习，现在我们做一个小小的总结。

先说圆柱中的截面。

图1是圆柱的轴截面，AB是不垂直于轴的截面，分别与圆柱的内切球切于点C、D，E、F是球与圆柱的切点，根据球切线的性质，AC=AE，AD=AF，AC=BD，所以AB=EF。

图2是圆柱的直观图，P是截面边线上的任意一点，过P作圆柱的母线，分别切两球于点M、N，因为PC=PM，PD=PN，所以PC+PD=PM+PN=MN=EF=AB，即点P的到定点C、D的距离之和为定值AB，且AB>CD，根据椭圆的定义，截面就是一个椭圆面，椭圆面的焦点是C、D，长轴是AB。

再说圆锥中的截面，情况要复杂一些。

在图3、图4中，截面AB与圆锥如图相交，并且AB=EF。

在切面边线上任取一点P，过P作圆锥母线，分别切两圆于M、N两点，与圆柱情况一样，PC+PD=PM+PN=MN=EF=AB，点P的到定点C、D的距离之和为定值CD，截面也是一个椭圆面，椭圆面的焦点是C、D，长轴是AB。

再看图5、图6，截面AB与母线GH平行，内切球分别与圆锥、截面切于点C、E、F，过E、F平行于底面的平面与截面AB延展相交于直线D，由图可知，BD=KF。

在截面AB的边线上任取一点P，过P作圆锥母线，切内切球于M，则有PM=PC。

过P作平行于底面的截面O，交母线于N。

过P作直线D的垂线段，垂线段与OD平行且相等，又PM=NF=OD，所以点P到点C的距离等于到直线D的距离，根据抛物线的定义，此时的截面应是抛物线面，焦点是C，准线是直线D。

最后看图7、图8，截面AB与轴平行，内切球分别与圆锥、截面切于点C、D、E、F，根据球切线的性质，AC=AE，AD=AF，AC-AD=AF-AE，即AB=EF。

在截面AB的边线上任取一点P，过P作圆锥母线，切内切球于M、N，则有PC=PM，PD=PN。

圆柱与圆锥的切截面的性质与计算公式圆柱和圆锥是几何学中常见的几何体，它们具有一些特殊的性质，其中之一就是它们的切截面。

在本文中，我们将研究圆柱和圆锥的切截面的性质，并探讨计算其面积和体积的公式。

一、圆柱的切截面性质1. 圆柱的切割平面可以得到圆形切截面。

当一个平面与圆柱的侧面相交时，切割下来的切截面是一个圆形。

这是因为圆柱的侧面是由一条平行于圆底的直线轨迹沿着圆底的圆形所生成。

因此，任何平行于圆底的平面与圆柱相交时，都会产生一个圆形的切截面。

2. 圆柱的切割平面可以得到椭圆形切截面。

当一个斜面与圆柱的侧面相交时，切割下来的切截面是一个椭圆形。

这是因为斜面切割下来的轨迹是由一个平行于圆底的直线沿着一个椭圆底面生成的。

因此，当一个斜面与圆柱相交时，切割下来的切截面是一个椭圆形。

3. 圆柱的切割平面可以得到矩形切截面。

当一个垂直于圆底的平面与圆柱的侧面相交时，切割下来的切截面是一个矩形。

这是因为垂直于圆底的平面与圆柱的侧面相交时，切割下来的形状是一个长方形。

二、圆柱的切截面的计算公式1. 圆形切截面的面积和周长计算公式圆形的切截面是一个半径不等于0的圆。

其面积可以使用公式πr²来计算，其中r为切割圆的半径；周长可以使用公式2πr来计算。

2. 椭圆形切截面的面积和周长计算公式椭圆的切截面是一个半径不等于0的椭圆。

其面积可以使用公式πab来计算，其中a和b分别为切割椭圆的长轴和短轴的长度；周长的计算没有简单的公式，需要使用数值或数值逼近的方法进行计算。

3. 矩形切截面的面积和周长计算公式矩形的切截面是一个长和宽都不等于0的矩形。

其面积可以使用公式lw来计算，其中l和w分别为切割矩形的长度和宽度；周长可以使用公式2(l+w)来计算。

三、圆锥的切截面性质1. 圆锥的切割平面可以得到圆形切截面。

当一个平面与圆锥的侧面相交时，切割下来的切截面也是一个圆形。

与圆柱不同的是，在圆锥中，不仅侧面可以得到圆形切截面，底面也可以得到圆形切截面。