量子遗传算法流程图

第6章 计算智能 163（5）随着迭代次数的增加，适应度函数变化即函数()10sin(5)7cos(4)f x x x x =++取得最大值的过程如图6.7所示。

图6.7 粒子群算法的适应度函数曲线变化通过上述粒子群优化计算，最终获得式6.35目标函数的最优解为7.8569x =，()24.8554f x =。

6.3 量子进化算法6.3.1 量子进化算法量子进化算法建立在量子态矢量表达基础上，将量子比特的概率矢量表示应用于染色体的编码，使得一条量子染色体可以表达多个态的叠加，并利用各种量子门实现染色体的更新操作，从而实现目标求解。

2000年，Kuk-Hyun Han 将量子态矢量表达引入染色体编码中，通过量子门旋转实现染色体更新，提出了遗传量子算法（Genetic Quantum Algorithm ，GQA ），并通过对背包问题的优化计算，取得了比常规遗传算法更好的效果。

针对GQA 的不足，Han 在2002年通过改进量子门旋转角度策略和引入移民策略，提出了量子进化算法（Quantum Evolutionary Algorithm ，QEA ）。

由于量子进化算法具有多样性特征，在参数优化计算的过程中可以获得更好的结果，目前已经应用到数值优化、组合优化、图形图像处理、电路设计、通信、多目标优化等领域。

6.3.2 量子进化算法原理量子进化算法采用量子位编码来表示染色体，通过量子门更新种群完成进化搜索。

与传统进化算法相比，它具有种群规模小、收敛速度较快、全局寻优能力强的特点。

下面介绍量子进化算法的原理。

1．QEA 算法基本操作（1）量子染色体编码在量子计算中，采用量子位表示最小的信息单元，一个量子位可以处于“1”态、“0”态。

量子遗传算法 1.遗传算法 遗传算法是一种模拟达尔文生物进化论和遗传变异的智能算法。

这种算法具有鲁棒性（用以表征控制系统对特性或参数扰动的不敏感性）较强，实现的步骤规范、简单通用等优点，在人工智能、多目标决策、社会及经济等领域都有大量运用。

但一般遗传算法存在一定得局限性：收敛速度慢、迭代的次数多，易过早收敛，容易陷入局部最优解。

2.量子计算量子计算为量子力学与信息科学的综合交叉学科。

量子计算具有量子力学的并行性，计算速度更快；同时，量子状态多种多样，在进行最优解的搜索时极少陷入局部的极值。

3.量子遗传算法量子遗传算法将量子的态矢量引入遗传算法，利用量子比特的概率幅应用于染色体的编码。

一条染色体是多个量子状态的叠加。

并使用量子旋转门实现染色体的变异更新。

因此量子遗传算法具有迭代次数少，运行速度快，能以较少种群进行遗传变异，搜索范围广，难以陷入局部的极值等优点。

4.操作步骤1）运用量子比特初始化父代染色体2）在量子遗传算法中，染色体采用量子位的概率幅进行编码，编码方案如下：1212cos()cos()cos()sin()sin()sin()i i ik i i i ik P θθθθθθ⎡⎤=⎢⎥⎣⎦ k j n i rand ij ,...,2,1,,...,2,1,2==⨯=πθ3）对初始化种群中的每一个个体进行测量。

4）对每个测量值进行适应度的评估，以适应度来选择最优个体，进行遗传变异。

5）使用量子旋转门进行下一代个体的更新，量子旋转门为逻辑门中一种较为常用的方法，具体表示为：⎪⎪⎭⎫ ⎝⎛-=i i i i u θθθθθcos sin sin cos )( 6）进行迭代1+=y y7）达到终止设定条件，输出最佳个体，得到最优解。

运行结果：。

量子遗传算法matlab量子遗传算法是一种结合了量子计算和遗传算法的优化方法。

它利用量子比特的特性，如叠加和纠缠，来提高搜索效率。

下面是一个简单的Matlab代码示例，用于演示如何实现一个基本的量子遗传算法。

请注意，这只是一个示例代码，可能需要根据您的具体需求进行修改和优化。

```matlab% 参数设置pop_size = 100; % 种群大小chrom_length = 5; % 染色体长度max_gen = 100; % 最大迭代次数cross_rate = 0.7; % 交叉概率mutate_rate = 0.01; % 变异概率bit_flip_probability = 0.01; % 量子比特翻转概率% 初始化种群pop = round(rand(pop_size, chrom_length));% 主循环for gen = 1:max_gen% 量子遗传算法操作for i = 1:pop_size% 量子比特编码qubit_state = pop(i, :);qubit_state = qubit_state / norm(qubit_state); % 归一化qubit_state = qubit_state(:, [2 3]); % 取第二个和第三个量子比特作为编码的二进制数bit_state = reshape(qubit_state, 2^length(qubit_state), []);bit_state = bit_state / norm(bit_state); % 归一化bit_state = bit_state(:); % 展平bit_state = bit_state(bit_flip_probability > rand); % 量子比特翻转bit_state = reshape(bit_state, [2^length(bit_state) length(bit_state)]); % 重塑为矩阵形式qubit_state = bit2qubit(bit_state); % 二进制数转量子比特态% 量子旋转门操作theta = -10*pi + 2*pi*rand; % -10 到10之间的随机角度U = exp(-i*theta*(2/pi)*X); % X是X门，根据角度计算旋转门矩阵qubit_state = U*qubit_state; % 应用旋转门操作% 量子测量操作，得到适应度值measurement = expval(Z); % Z是Z门，测量结果为适应度值end% 选择操作，根据适应度值选择个体进行交叉和变异操作% ...% 交叉操作，根据交叉概率进行交叉操作，生成新的个体% ...% 变异操作，根据变异概率进行变异操作，生成新的个体% ...end```请注意，这个代码只是一个基本示例，实际上实现量子遗传算法还需要更多的细节和步骤，如选择操作、交叉操作和变异操作等。

量子遗传算法基本过程-概述说明以及解释1.引言1.1 概述量子遗传算法是一种结合了量子计算与遗传算法的新型优化算法。

遗传算法是一种模仿生物进化原理的搜索算法，而量子计算则是基于量子比特的计算方式。

量子遗传算法的基本原理是利用量子比特的叠加和纠缠特性来增强搜索的能力，从而提高优化问题的求解效率。

本文将对量子遗传算法的基本过程进行详细介绍，包括量子计算的简介、遗传算法的概述以及量子遗传算法的基本过程。

通过对这些内容的讲解，读者可以深入了解量子遗传算法的工作原理，并且了解其在优化问题中的应用前景和未来发展方向。

1.2 文章结构文章结构部分：本文将首先介绍量子计算的基本概念和原理，然后对遗传算法进行概述，介绍其基本运行过程。

最后，着重详细探讨量子遗传算法的基本过程，包括其具体的实现步骤和核心原理。

通过对这些内容的深入阐述，读者将能够全面了解量子遗传算法的基本运行机制和实际应用价值。

内容1.3 目的目的部分的内容:本文旨在深入探讨量子遗传算法的基本过程，通过介绍量子计算和遗传算法的基本概念，以及它们在量子遗传算法中的应用，帮助读者理解量子遗传算法的原理和运行机制。

同时，我们将分析量子遗传算法在实际问题中的应用前景，展望其在优化、搜索和机器学习等领域的发展方向，以期为相关研究和应用提供理论支持和启发。

2.正文2.1 量子计算简介量子计算是利用量子力学原理来进行计算的一种新型计算方式。

与传统计算不同的是，量子计算利用量子比特（Qubit）来存储信息，而不是传统计算中的比特（Bit）。

在量子计算中，量子比特可以同时处于多种状态，这种特性被称为叠加态。

另外，量子计算还利用了纠缠和量子隐形传态等量子效应来进行计算，使得量子计算机具有远超经典计算机的计算速度和效率。

量子计算的基本原理是量子叠加态和量子纠缠，利用这些特性可以在同一时刻处理多种可能性，从而大大加快计算速度。

量子计算机在处理一些传统计算机难以解决的问题时显示出了强大的优势，比如在大数据处理、密码学、化学模拟等方面均有潜在的运用前景。

三分钟学会遗传算法遗传算法此节介绍最著名的遗传算法(GA)。

遗传算法属于进化算法，基本思想是取自“物竞天泽、适者生存”的进化法则。

简单来说，遗传算法就是将问题编码成为染色体，然后经过不断选择、交叉、变异等操作来更新染色体的编码并进行迭代，每次迭代保留上一代好的染色体，丢弃差的染色体，最终达到满足目标的最终染色体。

整个流程由下图构成（手写，见谅 -_-!!）流程图步骤由以下几步构成：编码（coding）——首先初始化及编码。

在此步，根据问题或者目标函数（objective function）构成解数据（solutions），在遗传算法中，该解数据就被称为染色体（chromosome）。

值得一提的是，遗传算法为多解（population based）算法，所以会有多条染色体。

初始化中会随机生成N条染色体，, 这里表示染色体包含了n条。

其中，这里表示第i条染色体由d维数值构成。

GA会以这个N个数据作为初始点开始进行进化。

评估适应度（evaluate fitness）——这一步用染色体来进行目标函数运算，染色体的好坏将被指明。

选择（selection）——从当前染色体中挑选出优良的个体，以一定概率使他们成为父代进行交叉或者变异操作，他们的优秀基因后代得到保留。

物竞天择这里得以体现。

交叉（crossover）——父代的两个两个染色体，通过互换染色体构成新的染色体。

例如下图，父亲母亲各提供两个基因给我。

这样我既保留了父母的基于，同时又有自己的特性。

交叉变异（mutation）——以一定概率使基因发生突变。

该算子一般以较低概率发生。

如下图所示：变异下面我们将一步一步为各位呈现如何用matlab编写一个简单的GA算法。

本问题为实数最小化minimization问题。

我们需要在解空间内找到最小值或近似最小值，此处我们使用sphere函数作为目标函数（读者可以自行修改为其他的目标函数）。

sphere function•初始化：在这一步中，我们将在给定问题空间内生成随机解，代码如下：% %% 初始化% % 输入：chromes_size，dim维数,lb下界，ub 上界% % 输出：chromes新种群function chromes=init_chromes(chromes_size,dim,lb,ub) % 上下界中随机生成染色体 chromes = rand(chromes_size,dim)*(ub-lb)+lb;end•选择：选择是从当前代中挑选优秀的染色体保留以繁殖下一代。

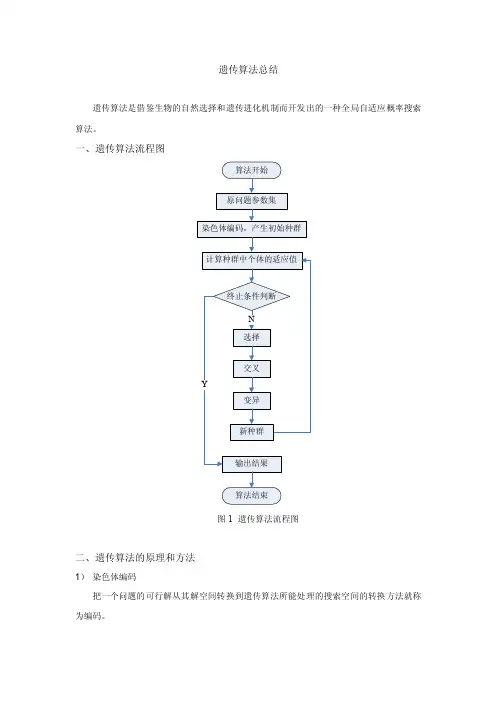
遗传算法总结遗传算法是借鉴生物的自然选择和遗传进化机制而开发出的一种全局自适应概率搜索算法。

一、遗传算法流程图算法开始原问题参数集染色体编码，产生初始种群计算种群中个体的适应值终止条件判断N选择交叉Y变异新种群输出结果算法结束图1 遗传算法流程图二、遗传算法的原理和方法1）染色体编码把一个问题的可行解从其解空间转换到遗传算法所能处理的搜索空间的转换方法就称为编码。

De Jong 曾提出了两条操作性较强的实用编码原则：编码原则一：应使用能易于产生与所求问题相关的且具有低阶、短定义长度模式的编码方案；编码原则二：应使用能使问题得到自然表示或描述的具有最小编码字符集的编码方案。

编码方法主要有以下几种：二进制编码方法、格雷码编码方法、浮点数编码方法、符号编码方法、参数级联编码方法、多参数交叉编码方法。

2） 适应值计算由解空间中某一点的目标函数值()f x 到搜索空间中对应个体的适应度函数值(())Fit f x 的转换方法基本上有一下三种： a ． 直接以待解的目标函数值()f x 转化为适应度函数值(())Fit f x ，令() (())=() f x Fit f x f x ⎧⎨-⎩目标函数为最大化函数目标函数为最小化函数b ． 对于最小值的问题，做下列转化max max () () (())0 C f x f x C Fit f x -<⎧=⎨⎩其他，其中max C 是()f x 的最大输入值。

c ． 若目标函数为最小值问题，1(()), 0, ()01()Fit f x c c f x c f x =≥+≥++ 若目标函数为最大值问题，1(()), 0, ()01()Fit f x c c f x c f x =≥-≥+- 3） 选择、交叉、变异遗传算法使用选择算子来对群体中的个体进行优胜劣汰操作：根据每个个体的适应度值大小选择。

适应度较高的个体被遗传到下一代群体中的概率较大；适应度较低的个体的被遗传到下一代群体中的概率较小。

关于量子遗传算法的杂七杂八遗传算法确实太有名了，无论是数学建模的培训中还是机器学习的项目中，经常性能看到遗传算法（GA）活跃的身影，其用途十分广泛，而且MATLAB或者是Python的实现遗传算法功能的工具箱也很多，笔者就一度使用北卡罗莱纳大学提供的免费工具箱实现了对于BP神经网络的初始化权值与阈值的优化，效果十分不错，而且实现起来不那么费劲，所以还是挺受好评的，对于写毕业论文的同志而言，如果实在不知道强行套用第三方算法对于原本的算法进行升级该怎么做，有两个万金油组合，一个是AHP，另一个就是几乎无所不能的GA，当然了，如果需要对于矩阵进行降维操作首选一定是PCA。

1 关于GA算法的种种1.1简介顾名思义，学过高中生物的都应该可以理解“遗传”是什么，染色体变异、染色体交叉等术语应该也能够大概知道是什么意思。

其实遗传算法主要就是模拟这一个过程。

不过，笔者觉得本算法中的核心部分中的变异与交叉的情节，其实达尔文这个姐控的贡献不是很大，最早提出相关的概念完成了相关的建模的是孟德尔所谓物竞天择适者生存，这个对于现实生活中的生物适用，对于具有特定含义的矩阵肯定也是适用的，当然了，反映他们到底多么“适应”的函数就是所谓的适应度函数，虽然关于适应度函数的取法现在并没有十分固定的一以贯之的通用公式1.2四个基本概念遗传算法中，一个基本单位为“个体”，一个种群（系统）中拥有好多个体。

每个个体携带两个内容：染色体与适应度。

当然了，这个时候上述的这些概念根本没有机器学习的含义，而全然为生物的含义或者用生物上的话来说，每一个生物都有染色体，染色体决定了他们表现出来的性状是怎样的。

所以说，染色体决定了每一个生物的肥瘦程度。

因此我们建立以下对应关系：整个牧场-> 一个种群，在机器学习中可以理解为具有实际项目含义的构成所有矩阵的cluster一头羊->一个个体，在机器学习的大背景下可以理解成矩阵，就是MATLAB里面的mat文件某头羊决定肥瘦程度的染色体->该个体的染色体，在机器学习的大背景下可以理解成mat 文件中的某一行或者是某一列。