时间序列中的ARMA模型共40页
- 格式:ppt
- 大小:1.94 MB
- 文档页数:40



第五讲(续)平稳时间序列的ARMA模型1 平稳性有一类描述时间序列的重要随机模型受到了人们的广泛关注,这就是所谓的平稳模型。
这类模型假设随机过程在一个不变的均值附近保持平衡。
其统计规律不会随着时间的推移发生变化。
平稳的定义分为严平稳和宽平稳。
定义1(严平稳)设{},t x t T ∈是一个随机过程,t x 是在不同的时刻t 的随机变量,在不同的时刻t 是不同的随机变量,任取n 个值1,,n t t K 和任意的实数h ,则1,,n x x K 分布函数满足关系式1111(,,;,)(,,;,)n n n n n n F x x t t F x x t h t h =++L L L L则称{},t x t T ∈为严平稳过程。
在实际中,这几乎是不可能的。
由此考虑到是否可以把条件放宽,仅仅要求其数字特征(数学期望和协方差)相等。
定义2(宽平稳)若随机变量{},t x t T ∈的均值(一阶矩)和协方差(二阶矩)存在,且满足:(1)任取t T ∈,有()t E x c =; (2)任取t T ∈,t T τ+∈,有[(())(())]()E X t a X t a R ττ-+-=协方差是时间间隔的函数。
则称{},t x t T ∈ 为宽平稳过程,其中()R τ为协方差函数。
2 各种随机时间序列的表现形式白噪声过程(white noise ,如图1)。
属于平稳过程。
y t = u t , u t ~ IID(0, σ2)图1 白噪声序列(σ2=1)随机游走过程(random walk,如图11)。
属于非平稳过程。
y t = y t-1 + u t, u t~ IID(0, σ2)图2 随机游走序列(σ2=1)图3 日元兑美元差分序列图4股票综合指数图5随机趋势非平稳序列(μ= 0.1)图6 随机趋势非平稳序列(μ= -0.1)图7 对数的中国国民收入序列图8 中国人口序列3 延迟算子延迟算子类似于一个时间指针,当前序列值乘以一个延迟算子,就相当于把当前序列值的时间向过去拨了一个时刻,记B 为延迟算子,有,1p t p t x B x p -=∀≥。
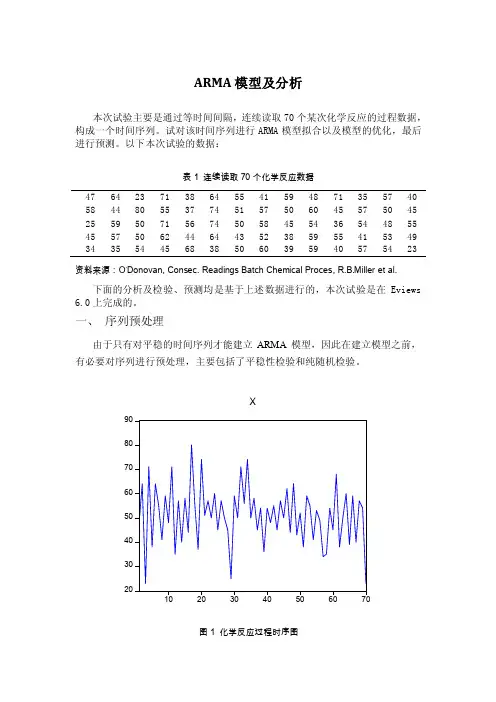
ARMA模型及分析本次试验主要是通过等时间间隔,连续读取70个某次化学反应的过程数据,构成一个时间序列。
试对该时间序列进行ARMA模型拟合以及模型的优化,最后进行预测。
以下本次试验的数据:表1 连续读取70个化学反应数据47 64 23 71 38 64 55 41 59 48 71 35 57 4058 44 80 55 37 74 51 57 50 60 45 57 50 4525 59 50 71 56 74 50 58 45 54 36 54 48 5545 57 50 62 44 64 43 52 38 59 55 41 53 4934 35 54 45 68 38 50 60 39 59 40 57 54 23 资料来源:O’Donovan, Consec. Readings Batch Chemical Proces, ler et al.下面的分析及检验、预测均是基于上述数据进行的,本次试验是在Eviews 6.0上完成的。
一、序列预处理由于只有对平稳的时间序列才能建立ARMA模型,因此在建立模型之前,有必要对序列进行预处理,主要包括了平稳性检验和纯随机检验。
图1 化学反应过程时序图序列时序图显示此化学反应过程无明显趋势或周期,波动稳定。
见图1。
图2 化学反应过程相关图和Q统计量从图2的序列的相关分析结果:1. 可以看出自相关系数始终在0周围波动,判定该序列为平稳时间序列2.看Q统计量的P值:该统计量的原假设为X的1期,2期……k期的自相关系数均等于0,备择假设为自相关系数中至少有一个不等于0,因此如图知,该P值在滞后2、3、4期是都为0,所以拒接原假设,即序列是非纯随机序列,即非白噪声序列(因为序列值之间彼此之间存在关联,所以说过去的行为对将来的发展有一定的影响,因此为非纯随机序列,即非白噪声序列)。
二、模型识别由于检验出时间序列是平稳的,且是非白噪声序列,因此可以建立模型,在建立模型之前需要识别模型阶数即确定阶数。







一案例分析的目的本案例选取2001年1月,到2013年我国铁路运输客运量月度数据来构建ARMA模型,并利用该模型进行外推预测分析。
二、实验数据数据来自中经网统计数据库2013-04 1.75 2013-05 1.62 2013-06 1.80 2013-07 1.99 2013-08 2.03 2013-09 1.92 2013-10 1.64数据来源:中经网数据库三、ARMA模型的平稳性首先绘制出N的折线图,如图从图中可以看出,N序列具有较强的非线性趋势性,因此从图形可以初步判断该序列是非平稳的。
此外,N在每年同期出现相同的变动方式,表明N还存在季节性特征。
下面对N 的平稳性和季节季节性进行进一步检验。
四、单位根检验为了减少N 的变动趋势以及异方差性,先对N进行对数处理,记为LN其曲线图如下:GENR LN = LOG(N)对数后的N趋势性也很强。
下面观察N 的自相关表,选择滞后期数为36,如下:从上图可以看出,LN的PACF只在滞后一期是显著的ACF随着阶数的增加慢慢衰减至0,因此从偏/自相关系数可以看出该序列表现一定的平稳性。
进一步进行单位根检验,打开LN选择存在趋势性的形式,并根据AIC自动选择滞后阶数,单位根检验结果如下:T统计值的值小于临界值,且相伴概率为0.0001,因此该序列不存在单位根,即该序列是平稳序列。
五、季节性分析趋势性往往会掩盖季节性特征,从LN的图形可以看出,该序列具有较强的趋势性,为了分析季节性,可以对LN进行差分处理来分析季节性:Genr = DLN = LN – LN (-1)观察DLN的自相关表,如下:DLN在之后期为6、12、18、24、30、36处的自相关系数均显著异于0,因此,该序列是以周期6呈现季节性,而且季节自相关系数并没有衰减至0,因此,为了考虑这种季节性,进行季节性差分:GENR SDLN = DLN –DLN(-6)再做关于SDLN的自相关表,如下:SDLN在滞后期36之后的季节ACF和PACF已经衰减至0,下面对SDLN建立SARMA模型。
第1节 时间序列ARMA 模型一、时间序列及其特征识别(一)地理时间序列的分类与构成1.地理系统中的时间序列如果对地理系统进行长期观测,每隔一定的时间作一个记录,则记录结果可以构成时间序列。
如果只针对某一个指标进行观测,得到的记录为一元时间序列;如果同时观测多个指标,则可形成多元时间序列。
因此,所谓时间序列(time series ),实际上就是将某个指标在不同时刻的不同数值,按照时间先后的顺序排列而成的数列。
时间序列分析就是利用这组数列,应用数理统计方法加以处理,以预测未来事物的发展。
地理系统的演化过程一般包含两种成分,一是确定性成分,二是随机性成分。
确定性成分具有一定的物理意义,它们又包括周期成分和非周期成分,其坐标曲线具有比较明确的规则;随机成分则表现得没有规则,其坐标曲线似乎是任意摆动和振荡的轨迹,这种轨迹很难从物理上进行阐释,只能借助随机过程理论和方法予以分析。
随机时间序列通常包括平稳和非平稳两种情况,二者的性质有很大不同。
简而言之,时间序列的分类和构成可以图示如下(图4-1-1)。
这种分类不是特别严格的,它们之间的界限有时很难区分。
例如,有些学者将周期性序列视为广义的平稳序列。
地理时间序列{确定型{ 周期型序列{简单周期复合周期 非周期序列{ 准周期序列 暂态序列{趋势型序列跳跃型序列突变型序列随机型{平稳序列{相依型序列独立型序列非平稳序列 图4-1-1 地理时间序列的分类与构成地理系统时间序列的周期性一般与地球的公转、太阳活动和月球绕转有关,因此自然地理的许多现象如江河的水位、生物的发育都具有一定的季节性。
与此相关,许多人文地理现象由于生态环境的季节变化也表现出明确的周期规律,例如风景旅游地的游客人数具有季节性特征。
认识自然变化的周期性规律有时是非常重要的,例如,早在80 年代,浙江省气象研究所就有人(田清鉴)研究发现,1887 年、1909 年、1931 年、1954 年、1975 年,我国长江、黄淮海流域都曾发生特大洪水,时间间隔平均约为22 年,与太阳黑子的22 年周期有关,由此可以推断,1997 年前后还会发生特大洪水。