当前位置：文档之家 › 平面与直线及两平面的相对位置关系

平面与直线及两平面的相对位置关系

  • 格式：ppt
  • 大小：757.00 KB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

第4章 直线与平面、平面与平面的相对位置

第4章 直线与平面、平面与平面的相对位置

4.2 相交问题
【例4-5】 (1)求交点，如图4-9(c)所示。
①在铅垂线的水平投影上标出交点的水平投影k。
②在平面内过K点的水平投影k作辅助线ad，并求出它的正面 a′d′。
③a′d′与m′n′的交点即交点的正面投影k′。
4.2 相交问题
【例4-5】
(2)直线的可见性可利用重影点法来判断。因为直线是铅垂线， 水平投影积聚为一点，故不需要判别其可见性，只需判别直线 正面投影的可见性即可。直线以交点K为分界点，在平面前面 的部分可见，在平面后面的部分不可见。如图4-9(c)所示，选 取m′n′与b′c′的重影点1′和2′来判别。1点在MN上，2点在BC上， 从水平投影看，1点在前可见，2点在后不可见。即k′1′在平面 的前面可见，画成粗实线；其余部分不可见，画成虚线。
4.2 相交问题
3.一般位置平面与特殊位置平面相交
【例4-7】
求一般位置平面ABC与铅垂面P的交线MN及判别平面正面投 影的可见性，如图4-11(a)所示。 【解】分析：如前面所述，把求两个平面交线的问题看成是求 两个共有点的问题。所以欲求图4-11(b)中两个平面的交线，从 对图4-11(a)的分析来看，只要求出交线上的任意两点(如M和N) 即可。因为铅垂面的水平投影有积聚性，所以交线的水平投影 必然位于铅垂面的积聚投影上；交线的正面投影可利用线上定 点的方法求出。 作图步骤如下：
4.1.2 平面与平面平行 条件
若一个平面内的两条相交直线对应 平行于另一个平面内的两条相交直
线，则这两个平面平行。
4.1平行问题
1.两个一般位置平面平行
【例4-3】 过点E作一个平面与平面ABC平行，如图4-6(a)所示。
E ABC 作图步骤如图4-6(b)所示。 (1)过点E作ED∥AB(ed∥ab、e′d′∥a′b′)。 (2)过点E作EF∥AC(ef∥ac、e′f′∥a′c′)，则平面DEF 所求。

直线与平面、两平面的相对位置

直线与平面、两平面的相对位置
如果两个平面内的两条相交直线互相垂直，那么这两个平面互相垂直。
THANKS
感谢观看
04
直线与平面、两平面相对位置的性质
和定理
直线与平面垂直的性质和定理
直线与平面垂直的性质
如果一条直线垂直于一个平面，那么这 条直线上的任意一点到平面的距离都相 等。
VS
直线与平面垂直的定理
如果一条直线与平面内的两条相交直线都 垂直，那么这条直线与这个平面垂直。
直线与平面平行的性质和定理
直线与平面平行的性质
在构建过程中，需要充分考虑直线与平面的关系，以及两平 面之间的相对位置，以确保所构建的几何形状符合设计要求 。
建筑设计中的应用
在建筑设计中，直线与平面、两平面 的相对位置关系具有重要意义。通过 合理利用这些关系，可以设计出具有 独特美感和实用性的建筑作品。
例如，可以利用直线与平面的垂直关 系设计出高耸入云的摩天大楼，利用 两平面之间的角度关系创造出独特的 建筑造型。
直线与平面相交
总结词
当直线与平面有一个公共点时，直线 与平面相交。
详细描述
直线与平面相交意味着直线和平面在 某一点相遇。这个点是直线和平面的 唯一公共点。
直线与平面垂直
总结词
当直线的方向向量与平面的法向量平行时，直线与平面垂直。
详细描述
直线与平面垂直意味着直线与平面中的所有线段都垂直。在这种情况下，直线要么完全位于平面上，要么与平面 相交于一点。
应用
在几何学、物理学和工程学中，两平面垂直 的情况也经常出现，例如建筑物的墙与地面 、电路板上的线路与基板等。
03
直线与平面、两平面相对位置的应用
空间几何形状的构建
空间几何形状的构建是直线与平面、两平面相对位置在实际 应用中的重要体现。通过利用这些相对位置关系，可以构建 出各种复杂的空间几何形状，如球体、立方体、圆柱体等。

机械制图_5_直线、平面间的相对位置

机械制图_5_直线、平面间的相对位置
12/45
Liu Wei, Beijing Jiaotong University
两平面相交其交线为直线；交 几何特性是： 线是两平面的共有线；交线上 的点都是两平面的共有点。 推断 两平面相交的问题
2. 两平面相交
两组直线与平面相交的问题
需要解决：
三面共点的思想可有效 地用于求两平面的交线。
交线的求解方法： ⑴ 确定两平面的两个共有点； ⑵ 确定一个共有点及交线的方向。 判别可见性，即平面间的遮挡关系，交线是可见性的分界线
b' f'
空间分析：
a'
e' x a e
k’
l’
d'
c' c o
A E K B F L D C
k
f
l
界
d
前，可见
b V 面投影
a b
c
k l
投射方向
作图步骤 1) 用面上取线的方法求交线 2) 可见性：根据空间位置关系判别。其余部分可由推理得出可见性。
Chapter 5 Positions between Lines and Planes
B K A
(D )
a' E C d' x d b
e'
c' o
怎么求？ 辅助平面法
就是用辅助平面将一般位置直线与平面的求交问题，转 变为在同一平面内求两直线交点的问题，从而使原问题得到求解的方法。 下面通过例子说明如何使用辅助平面法
Chapter 5 Positions between Lines and Planes
c e m
9/45
h
求解步骤 作辅助线EK//AC 结论
a

画法几何与工程制图 第六章 直线与平面平面与平面的相对位置关系

画法几何与工程制图 第六章 直线与平面平面与平面的相对位置关系
a’
d’
c’
k’
f’
b’
e’
X
O
e
f
a(b)
k
d
c
15
（二）一般位置平面与特殊位置平面相交
求两平面交线的问题可以看作是
求两个共有点的问题,由于特殊位置
平面的某些投影有积聚性，交线可
直接求出。
16
例:已知两特殊位置平面相交，求交线的投影
返回
17
二、 辅助平面法
求作交线的步骤：
（一）直线与一般位置平面相交
Ⅰ
Ⅱ
Ⅳ Ⅲ
26
具体做图步骤
27
第三节 直线与平面垂直、两平面互相垂直
一、直线与平面垂直
(一)直线与一般位置平面垂直的关系 (二)直线与特殊位置平面垂直的关系
二、两平面互相垂直
28
（一）直线与平面垂直
Ⅰ Ⅱ
直线与一般位Leabharlann 平面29直线与一般位置平面
30
具体作法方法
31
例:过D点向三角形ABC作垂线
返回
10
(二）两个特殊位置平面互相平行
若两投影面垂直面或两投影面平行面互相平行时，则两平面 的同面积聚性投影（或迹线）互相平行。
11
第二节 直线与平面相交、平面与平面相交
一、积聚性法 （一）直线与特殊位置平面相交
（二）平面与特殊位置平面相交 二、 辅助平面法 （一）直线与一般位置平面相交 （二）两个一般位置平面相交
第六章 直线与平面、平面与平面的相对关系
第一节 直线与平面平行、平面与平面平行 第二节 直线与平面相交、平面与平面相交 第三节 直线与平面垂直、两平面互相垂直
1
第一节 直线与平面平行、平面与平面平行

直线与平面平面与平面的相对位置

直线与平面平面与平面的相对位置
解题过程： ①过b’作b’d’∥e’f’，求出db； ②检验bd是否与ef平行，
结论：平行
平面与平面的相对位置有:平行、相交和垂直三 种情况
二. 平面与平面平行
判定定理： 若一平面上的一对相交直线分别与另一平面上的
一对相交直线互相平行，则二平面平行。
E
D F
B A
C
若属于一平面的相交两直线对应平行于属于另一平面的相交两直 线，则此两平面平行
连接d’k’，延长后交
c’f’ 于m’点；
2）由m’ 得m，连 接dm与ab交得k；
3）根据重影点Ⅰ、 Ⅱ判别可见性。
3. 一般位置线与一般位置面相交
〖例〗如图所示，求作直线MN和平面△ABC的交 点K，并判别投影的可见性。
作图步骤：
1）在V面投影图中 标出直线MN与AC、 AB的重影点1’、2’。
〖例〗已知空 间点M和平面ABCD 的两面投影,求作 过M点垂直于平面 ABCD的垂线MN的 投影
作图步骤：
1）作a’1’∥OX轴，求
得1’ 和1，过点m作a1
的垂线。
2）作a2∥OX轴，由2 得2’，过m’作a’2’的垂 线m’n’。
3）由n’得n点，将 m’n’和mn画成粗实线。
2．特殊位置的直线与平面垂直
2）由1’、2’ 得1、 2，连接12与mn交得 点k。
3）由k得k’。
4）根据重影点Ⅳ、 Ⅴ判别可见性。
二. 平面与平面相交
M
K
L
F
N
两平面的交线是一条直线，这条直线为两平面所共有
平面与平面相交的问题，主要是求交线和判别 可见性的问题。
1．两特殊位置平面相交
投影面垂直面相交： 两个平面的投影均积聚为直线，若两直线相交， 则空间两平面相交，交点即为两平面交线。（交 点必为该投影面垂直线）

工业设计 机械制图教程 直线与平面及两平面之间的相对位置

工业设计 机械制图教程 直线与平面及两平面之间的相对位置
§1—5 直线与平面及两平面之间的相对位置（只讲特殊情况） 一、平行问题 —— 直线∥直线、直线∥平面、平面∥平面。 1、直线与平面平行 定理①:若一直线平行于平面上的某一直线，则该直线必然与 平面平行。 例1、试过点K作一直线MN与△ABC平行。 b′ n′ 1′ c′ k′ m′ a′
a
1
Байду номын сангаасc m
2′ （1′）
k′ f′ f
c′
a′
a
1
2、其交点为直线与平面的公共点， 正面投影 那么根据点的从属性： 3、判别可见性，完善视图。
e
2k b
c
—4—
（二）、特殊位置直线与一般位置平面相交——求交点 e′ b′ 1、可直接求出交点的那个投影？ 水平投影
1′
k′
c′ c
a′
f′
e(f) (k) 1
2、交点为直线与平面所共有， 据平面内取点： 3、判别可见性，完善视图。
1 2
k′
n′ n m
k d
c
b
—3—
二、相交问题
线∩线——已学过： ① 线∩面——求交点的问题； 面∩面——求交线的问题。 掌 握 ②
求第三投影 或定比法判断。
1、求交点： 2、求交线； 3、判别可见性。 （一）、特殊位置平面与一般位置直线相交——求交点问题 b′ 1、可直接求出交点的那个投影？ 水平投影 e′
k
n
b ※本题当然可以直接作平行于三角形某一边的直线。
—1—
例2、过点A作平面平行于直线EF。 f′ b′ a′ a f
e′
e
c′ c b
定理②:若一直线平行于一投影面的垂直面，则直线的投影与平面 的有积聚性的投影平行（或皆有积聚性）。

第五章 直线、平面的相对位置

第五章 直线、平面的相对位置

本章讨论直线与平面、平面与平面的相对位置关系及其投影，包括以下内容：1)平行关系：直线与平面平行，两平面平行；2)相交关系：直线与平面相交，两平面相交；3)垂直关系：直线与平面垂直，两一般位置直线垂直和两平面垂直。

§1 平行关系1.1 直线与平面平行直线与平面平行的几何条件是：如果平面外的一直线和这个平面上的一直线平行，则此直线平行于该平面。

由于EF∥BD，且BD 是ABC 平面上的一直线，所以，直线EF平行于ABC 平面。

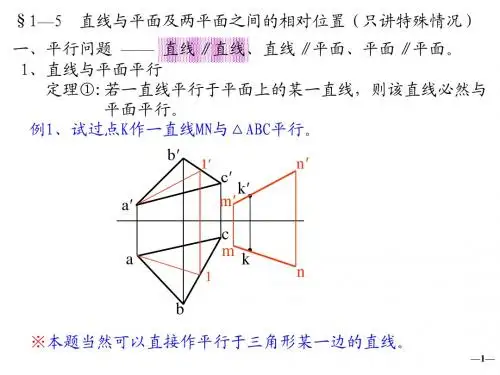
［例1］试过K点作一水平线，使之平行于△ABC。

先在△ABC上作一水平线AD；再过点K，作kl∥ad，k′l′∥a′d′，则直线KL为所求。

［例2］试过K 点作一正平线，使之平行于P 平面。

因P V 是P 平面上特殊的正平线，所以过点K 作KL ∥P V ，即作k ′l ′∥PV ，kl ∥X 轴，则直线KL 为所求。

［例3］试过K 点作一铅垂面P (用迹线表示)，使之平行于AB 直线。

由于铅垂面的H 投影为一直线，故若作铅垂面平行于AB 直线，则P H必平行于ab 。

因此，过k 作P H ∥ab ；过P X 作P V ⊥X 轴，则P 平面为所求。

1.2 平面与平面平行两平面相平行的条件是：如果一平面上的两条相交直线分别平行于另一平面上的两条相交直线，则此两平面平行。

两平行平面和第三个平面相交，其交线一定互相平行。

因此，两平行平面的同面迹线一定平行。

如果两平面的两对同面迹线分别互相平行，则不能肯定两平面是互相平行的。

如果平面的两条迹线是平行直线时，则一般要看第三个投影才能确定。

P 平面平行于Q 平面P 平面不平行于Q 平面［例1］过点K 作一平面，使之与AB、CD两平行直线表示的平面平行1：在AB、CD 平面上，作一条和AB、CD 不平行的辅助线，如AC ；2：过K 作KL∥AB ；3：过K 作KM∥AC ,则平面LKM即为所求。

［例2］过K 点作Q 平面(用迹线表示)，使之平行于P 平面。

平面与直线及两平面的相对位置关系PPT课件

平面与直线及两平面的相对位置关系PPT课件

二、 两平面相交（利用积聚性求交线）
两平面相交其交线为直线，交线是两平 面的共有线，同时交线上的点都是两平面的 共有点。
要解决的问题：
① 求两平面的交线 方法：⑴ 确定两平面的两个共有点。 ⑵ 确定一个共有点及交线的方向。
② 判别两平面之间的相互遮挡关系，即： 判别可见性。
第7页/共18页
平面与平面相交
n●
h
● 1(2)
c
作 图
① 求交线 ② 判别可见性
点Ⅰ在FH上，点Ⅱ在BC上，点Ⅰ在 上，点Ⅱ在下，故fh可见，n2不可见。
第10页/共18页
三. 直线与平面相交（利用辅助平面法求交点）
PV
1
k
2
步骤： 1．过EF作正垂平 面P。
2．求P平面与 ΔABC的交线ⅠⅡ。
3．求交线ⅠⅡ与 EF的交点K。
2
k
1
第11页/共18页
示意图
以铅垂面为辅助平面求线面交点。
2 k
1
步骤： 1．过EF作铅垂平 面P。
2．求P平面与 ΔABC的交线ⅠⅡ。
PH 1
3．求交线ⅠⅡ与 EF的交点K。
k 2
第12页/共18页
四、求两平面的交线
k 1 m m
k 1
PV n 2 e
2
l QV
两一般位置 平面相交，求交 线步骤：
s
f
k
e
m
n
r
r n
e k
m
Hale Waihona Puke fs第3页/共18页
第二节 相交问题
一、 直线与平面相交
直线与平面相交 平面与平面相交
交点是直线与平面的共有点 交点是直线可见与不可见的分界点。

工程制图-第三章-直线、平面的相对位置

工程制图-第三章-直线、平面的相对位置

直线、平面的相对位置本章讨论直线与平面、平面与平面的相对位置关系及其投影，包括以下内容：1)平行关系：直线与平面平行，两平面平行。

2)相交关系：直线与平面相交，两平面相交。

§1 平行关系1.1 直线与平面平行定理:若一直线平行于平面上的某一直线，则该直线与此平面必相互平行。

以，直线EF平行于ABC平面。

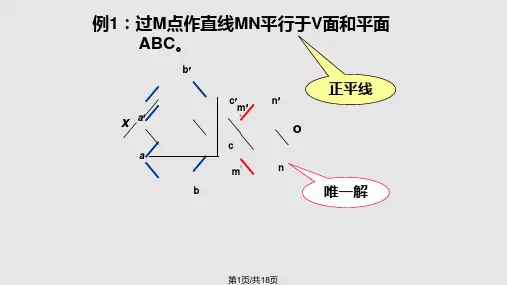
[例1]过已知点k ，作一条水平线平行于△ABC 平面。

步骤：1）在ABC 平面内作一水平线AD ； 2）过点K 作 KL ∥AD ； 3）直线KL即为所求。

d′d l′lk′k a′a b′e′bc X[例2]试判断:已知直线AB是否平行于四棱锥的侧表面SCF。

作图步骤：1）作c'm'∥a'b'；2）根据CM在平面SCF内，作出cm；3）由于cm不平行于ab，即在该平面内作不出与AB平行的直线，所以，直线AB不平行于四棱锥侧表面SCF。

1.2 平面与平面平行两平面相平行的条件是：如果一平面上的两条相交直线分别平行于另一平面上的两条相交直线，则此两平面平行。

所以：平面ABC 和平面DEF 相平行。

［例3］过点K作一平面，是其与平面ABC平行。

解：只要过K点作两条相交直线分别平行于△ABC的两条边，则这两条相交直线所确定的平面就是所求平面。

作图步骤：2）作KD∥AC(k'd'∥a'c',kd∥ac);a'cac'bb'k'kl'ld'dX1）作KL∥BC(k'l'∥b'c', kl∥bc); 3）平面KDL即为所求。

2.1 直线与平面相交2.1.1 利用积聚性求交点当平面或直线的投影有积聚性时，交点的两个投影中有一个可直接确定，另一个投影可用在直线上或平面上取点的方法求出。

⑴平面为特殊位置[例]求直线MN与平面ABC的交点K并判别可见性。

空间及投影分析平面ABC 是一正垂面，其V 投影积聚成一条直线，该直线与m'n'的交点即为K点的V 投影。

直线与平面相交PPT课件

直线与平面相交PPT课件

方法： 4. 两个一般位置平面相交（略）
1.求一平面与另一 平面的两直线 的交点（辅助 平面法）。
2.两交点的连线为 交线。
D
H
●A
M
●
B
N
●
●
C
E
F
.
16
作业：
P7： 4、5、6、8、9题
.
17
.
18
小结
重点掌握：
★ 点、直线、平面的投影特性，尤其是特殊位置直 线与平面的投影特性（积聚性）。
★ 点、直线、平面的相对位置的判断方法及投影特性。
一、直线上的点
⒈ 点的投影在直线的同面投影上。 ⒉ 点的投影必分线段的投影成定比——定比定理。
⒊ 判断方法
① 直线为一般位置时 ② 直线为特殊位置时
c b
a
a
k●
b
cb
a k●
a
b
.
19
二、两直线的相对位置
⒈ 平行
同名投影互相平行。
①
b
d
a
c
a
c
b
⑴ 平面为特殊位置
b
n
空间及投影分析
平面ABC是一铅垂面，
k
a
1(2) ●
●
m
m a
●2
●
●
1
b
k
其水平投影积聚成一条直
线，该直线与mn的交点即
c 为K点的水平投影。
作图
用线上
c ①求交点
取点法
②判别可见性
由水平投影可知，KN n 段在平面前，故正面投影
上kn为可见。
还可通过重影点判别可见性。
.
7
⑵ 直线为特殊位置

工程制图之直线与平面 平面与平面相对位置

工程制图之直线与平面 平面与平面相对位置
返回
A
Ⅰ
A
Ⅰ
D
Ⅱ
两平面垂直
D
Ⅱ
两平面不垂直
反之，两平面相互垂直，则由属于第一个平面的任意一点向第二个 平面作的垂线必属于第一个平面。
例1：平面由 BDF给定，试过定点K作平面的垂面。
h’ f’
c’
g’
k’
a’
b’
d’
a d
f c b
k g
h
返回
例2 、试判断 ABC与相交两直线KG和KH所给定的平面是否垂直。
a’ e’
f
2
a
b k
1
c
e
返回
例2 求直线EF与一般位置平面ΔABC的交点K。
f’
c’
b’ PH f
2’ k’
1’
a’ e’
步骤：
1、 过EF作铅垂面P。 2、求P平面与ΔABC 的交线ⅠⅡ。
3、求交线ⅠⅡ 与EF 的交点K。
a
1
b
k 2
c
e
返回
六、两一般位置平面相交求交线的方法
B M
K A
L F
点Ⅰ在FH上，点Ⅱ在BC上，点Ⅰ 在上，点Ⅱ在下，故fh可见，n2 不可见。
返回
五、直线与一般位置平面相交
M
A
例题1
C
例题2
B
N
判别可见性
返回
例1 求直线EF与一般位置平面ΔABC的交点K。
QV
c’
f’ 1’
k’ b’
2’
步骤：
1、 过EF作正垂面Q。 2、求Q平面与ΔABC 的交线ⅠⅡ。 3、求交线ⅠⅡ与EF 的交点K。
返回
例：求两平面的交线MN并判别可见性。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
作图
① 求交线 ② 判别可见性
从正面能影投否点影能不判上!用别可重？看出，
在交线左侧，平面ABC 在上，其水平投影可见。
例5 求两平面的交线MN并判别可见性。
b
e
m f ●
a e
a
b ●m
f
空间及投影分析
●n●1 ● 2
h
平面EFH是一水平面，它的
正面投影有积聚性。ab与ef
的交点m 、 b c与f h的交点
a
x
c
e
必相互平行。
d acb e
e f
o
f
e
f
h
o
h f
[例2] 已知定平面由平行两直线AB和CD给定。试过点K 作一平面平行于已知平面 。
s
f
k
e
m
n
r
r n
e k
m
f
s
第二节 相交问题
一、 直线与平面相交
直线与平面相交 平面与平面相交
交点是直线与平面的共有点 交点是直线可见与不可见的分界点。
② 判别两平面之间的相互遮挡关系，即： 判别可见性。
平面与平面相交
M
K
L
F
N
两平面的交线是一条直线，这条直线为两平面所共有
例4：求两平面的交线
MN并判别可见性。
⑴ a
b
e f
●
m(n) c
d
e
a
n
●
c
d
●m
b
f
如何判别？
可通过正面投影
直观地进行判别。
空间及投影分析
平面ABC与DEF都 为正垂面，它们的正面投 影都积聚成直线。交线必 为一条正垂线，只要求得 交线上的一个点便可作出 交线的投影。
c n即为两个共有点的正面投影，
故mn即MN的正面投影。
作图
n●
h
● 1(2)
c
① 求交线 ② 判别可见性
点Ⅰ在FH上，点Ⅱ在BC上， 点Ⅰ在上，点Ⅱ在下，故fh 可见，n2不可见。
三. 直线与平面相交（利用辅助平面法求交点）
PV
1
k
2
步骤： 1．过EF作正 垂平面P。
2．求P平面与 ΔABC的交线
● 求直线与平面的交点。
● 判别两者之间的相互遮挡关系，即判别可 见性。
例3 求直线MN与平面ABC的交点K并判别可见性。
⑴ 平面为特殊位置
b
n
空间及投影分析 平面ABC是一铅垂面，
k
a
1(2) ●
●
x m
其水平投影积聚成一条直 线，该直线与mn的交点即 c 为K点的水平投影。
作图
m ●2
① 求交点 c ② 判别可见性
ⅠⅡ。
3．求交线
ⅠⅡ与EF的交
2
点K。
k
1
示意图
以铅垂面为辅助平面求线面交点。
2 k 1
PH
1
步骤： 1．过EF作铅 垂平面P。
2．求P平面与 ΔABC的交线
ⅠⅡ。
3．求交线
ⅠⅡ与EF的交
点K。
k
2
四、求两平面的交线
k 1
PV n 2
e
两一般
l
位置平面相
QV 交，求交线
步骤：
1．用求直线
m
与平面交点
K F
H E
作图
PV
1 m
2
n
h
h n2 m1
1．过点K作平面 KMN// ABC平面。
2．求直线EF与平面 KMN的交点H 。
3．连接KH，KH即 为所求。
携手共进，齐创精品工程
Thank You
世界触手可及
谢谢观赏！
2020/11/5
20
2
的方法，作
m
出两平面的
e k
两个共有点K、
E。
l
2．连接两个
共有点，画
1
出交线KE。
示意图
n
两平面相交，判别可见性
3
1 (2 )
利
用
4
重
影
点
判
2
别
可
见
3 (4 )
性
1
[例6] 试过K点作一直线平行于已知平面ΔABC，并与直线EF相交
分析
过已知点K作平面P平行于 ABC；直线EF与平面P交于H； 连接KH，KH即为所求。
平面与直线及两平面的相对位置关 系
例1：过M点作直线MN平行于V面和平面 ABC。
b
正平线
cm n
x a
●
o
c a
m●
n
b
唯一解
二、 两平面平行
① 若一平面上的两相
交直线对应平行于另 一平面上的两相交直
x a
线，则这两平面相互 平行。
a
b c d
c d
b具 有积聚性的那组投影
② 判别可见性
点Ⅰ位于平面上，在
前；点Ⅱ位于MN上，在
后。故k 2为不可见。
二、 两平面相交（利用积聚性求交线）
两平面相交其交线为直线，交线是两平 面的共有线，同时交线上的点都是两平面的 共有点。
要解决的问题：
① 求两平面的交线 方法：⑴ 确定两平面的两个共有点。 ⑵ 确定一个共有点及交线的方向。
●
a
●
1
b
k
由水平投影可知，KN n 段在平面前，故正面投
影上kn为可见。
还可通过重影点判别可见性。
⑵ 直线为特殊位置
b m
空间及投影分析 直线MN为铅垂线，其
k●
水平投影积聚成一个点，
a
c ●1(2)
故交点K的水平投影也积聚
n
在该点上。
x b
作图
a
mk(●●n2) ● 1
① 求交点
用面上取点法
c