吉林省长春市普通高中2018届高三质量检测(三)数学(理)试卷扫描版含答案
- 格式:doc
- 大小:1.74 MB
- 文档页数:10

2018年普通高等学校招生全国统一考试数学试题理(全国卷1)注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设,则A. B. C. D.【答案】C【解析】分析:首先根据复数的运算法则,将其化简得到,根据复数模的公式,得到,从而选出正确结果.详解:因为,所以,故选C.点睛:该题考查的是有关复数的运算以及复数模的概念及求解公式,利用复数的除法及加法运算法则求得结果,属于简单题目.2. 已知集合,则A. B.C. D.【答案】B【解析】分析:首先利用一元二次不等式的解法,求出的解集,从而求得集合A,之后根据集合补集中元素的特征,求得结果.详解:解不等式得,所以,所以可以求得,故选B.点睛:该题考查的是有关一元二次不等式的解法以及集合的补集的求解问题,在解题的过程中,需要明确一元二次不等式的解集的形式以及补集中元素的特征,从而求得结果.3. 某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是A. 新农村建设后,种植收入减少B. 新农村建设后,其他收入增加了一倍以上C. 新农村建设后,养殖收入增加了一倍D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半【答案】A【解析】分析:首先设出新农村建设前的经济收入为M,根据题意,得到新农村建设后的经济收入为2M,之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得到其相应的关系,从而得出正确的选项.详解:设新农村建设前的收入为M,而新农村建设后的收入为2M,则新农村建设前种植收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以A项不正确;新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以B项正确;新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;新农村建设后,养殖收入与第三产业收入的综合占经济收入的,所以超过了经济收入的一半,所以D正确;故选A.点睛:该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图,要会从图中读出相应的信息即可得结果.4. 设为等差数列的前项和,若,,则A. B. C. D.【答案】B详解:设该等差数列的公差为,根据题中的条件可得,整理解得,所以,故选B.点睛:该题考查的是有关等差数列的求和公式和通项公式的应用,在解题的过程中,需要利用题中的条件,结合等差数列的求和公式,得到公差的值,之后利用等差数列的通项公式得到与的关系,从而求得结果.5. 设函数,若为奇函数,则曲线在点处的切线方程为A. B. C. D.【答案】D【解析】分析:利用奇函数偶此项系数为零求得,进而得到的解析式,再对求导得出切线的斜率,进而求得切线方程.详解:因为函数是奇函数,所以,解得,所以,,所以,所以曲线在点处的切线方程为,化简可得,故选D.点睛:该题考查的是有关曲线在某个点处的切线方程的问题,在求解的过程中,首先需要确定函数解析式,此时利用到结论多项式函数中,奇函数不存在偶次项,偶函数不存在奇次项,从而求得相应的参数值,之后利用求导公式求得,借助于导数的几何意义,结合直线方程的点斜式求得结果.6. 在△中,为边上的中线,为的中点,则A. B.C. D.【答案】A【解析】分析:首先将图画出来,接着应用三角形中线向量的特征,求得,之后应用向量的加法运算法则-------三角形法则,得到,之后将其合并,得到,下一步应用相反向量,求得,从而求得结果.详解:根据向量的运算法则,可得,所以,故选A.点睛:该题考查的是有关平面向量基本定理的有关问题,涉及到的知识点有三角形的中线向量、向量加法的三角形法则、共线向量的表示以及相反向量的问题,在解题的过程中,需要认真对待每一步运算.7. 某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点在正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,从到的路径中,最短路径的长度为A. B.C. D. 2【答案】B【解析】分析:首先根据题中所给的三视图,得到点M和点N在圆柱上所处的位置,点M在上底面上,点N 在下底面上,并且将圆柱的侧面展开图平铺,点M、N在其四分之一的矩形的对角线的端点处,根据平面上两点间直线段最短,利用勾股定理,求得结果.详解:根据圆柱的三视图以及其本身的特征,可以确定点M和点N分别在以圆柱的高为长方形的宽,圆柱底面圆周长的四分之一为长的长方形的对角线的端点处,所以所求的最短路径的长度为,故选B.点睛:该题考查的是有关几何体的表面上两点之间的最短距离的求解问题,在解题的过程中,需要明确两个点在几何体上所处的位置,再利用平面上两点间直线段最短,所以处理方法就是将面切开平铺,利用平面图形的相关特征求得结果.8. 设抛物线C:y2=4x的焦点为F,过点(–2,0)且斜率为的直线与C交于M,N两点,则=A. 5B. 6C. 7D. 8【答案】D【解析】分析:首先根据题中的条件,利用点斜式写出直线的方程,涉及到直线与抛物线相交,联立方程组,消元化简,求得两点,再利用所给的抛物线的方程,写出其焦点坐标,之后应用向量坐标公式,求得,最后应用向量数量积坐标公式求得结果.详解:根据题意,过点(–2,0)且斜率为的直线方程为,与抛物线方程联立,消元整理得:,解得,又,所以,从而可以求得,故选D.点睛:该题考查的是有关直线与抛物线相交求有关交点坐标所满足的条件的问题,在求解的过程中,首先需要根据题意确定直线的方程,之后需要联立方程组,消元化简求解,从而确定出,之后借助于抛物线的方程求得,最后一步应用向量坐标公式求得向量的坐标,之后应用向量数量积坐标公式求得结果,也可以不求点M、N的坐标,应用韦达定理得到结果.9. 已知函数.若g(x)存在2个零点,则a的取值范围是A. [–1,0)B. [0,+∞)C. [–1,+∞)D. [1,+∞)【答案】C【解析】分析:首先根据g(x)存在2个零点,得到方程有两个解,将其转化为有两个解,即直线与曲线有两个交点,根据题中所给的函数解析式,画出函数的图像(将去掉),再画出直线,并将其上下移动,从图中可以发现,当时,满足与曲线有两个交点,从而求得结果.详解:画出函数的图像,在y轴右侧的去掉,再画出直线,之后上下移动,可以发现当直线过点A时,直线与函数图像有两个交点,并且向下可以无限移动,都可以保证直线与函数的图像有两个交点,即方程有两个解,也就是函数有两个零点,此时满足,即,故选C.点睛:该题考查的是有关已知函数零点个数求有关参数的取值范围问题,在求解的过程中,解题的思路是将函数零点个数问题转化为方程解的个数问题,将式子移项变形,转化为两条曲线交点的问题,画出函数的图像以及相应的直线,在直线移动的过程中,利用数形结合思想,求得相应的结果.10. 下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.△ABC的三边所围成的区域记为I,黑色部分记为II,其余部分记为III.在整个图形中随机取一点,此点取自I,II,III的概率分别记为p1,p2,p3,则A. p1=p2B. p1=p3C. p2=p3D. p1=p2+p3【答案】A详解:设,则有,从而可以求得的面积为,黑色部分的面积为,其余部分的面积为,所以有,根据面积型几何概型的概率公式,可以得到,故选A.点睛:该题考查的是面积型几何概型的有关问题,题中需要解决的是概率的大小,根据面积型几何概型的概率公式,将比较概率的大小问题转化为比较区域的面积的大小,利用相关图形的面积公式求得结果.11. 已知双曲线C:,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若OMN为直角三角形,则|MN|=A. B. 3 C. D. 4【答案】B【解析】分析:首先根据双曲线的方程求得其渐近线的斜率,并求得其右焦点的坐标,从而得到,根据直角三角形的条件,可以确定直线的倾斜角为或,根据相关图形的对称性,得知两种情况求得的结果是相等的,从而设其倾斜角为,利用点斜式写出直线的方程,之后分别与两条渐近线方程联立,求得,利用两点间距离同时求得的值.详解:根据题意,可知其渐近线的斜率为,且右焦点为,从而得到,所以直线的倾斜角为或,根据双曲线的对称性,设其倾斜角为,可以得出直线的方程为,分别与两条渐近线和联立,求得,所以,故选B.点睛:该题考查的是有关线段长度的问题,在解题的过程中,需要先确定哪两个点之间的距离,再分析点是怎么来的,从而得到是直线的交点,这样需要先求直线的方程,利用双曲线的方程,可以确定其渐近线方程,利用直角三角形的条件得到直线的斜率,结合过右焦点的条件,利用点斜式方程写出直线的方程,之后联立求得对应点的坐标,之后应用两点间距离公式求得结果.12. 已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为A. B. C. D.【答案】A【解析】分析:首先利用正方体的棱是3组每组有互相平行的4条棱,所以与12条棱所成角相等,只需与从同一个顶点出发的三条棱所成角相等即可,从而判断出面的位置,截正方体所得的截面为一个正六边形,且边长是面的对角线的一半,应用面积公式求得结果.详解:根据相互平行的直线与平面所成的角是相等的,所以在正方体中,平面与线所成的角是相等的,所以平面与正方体的每条棱所在的直线所成角都是相等的,同理平面也满足与正方体的每条棱所在的直线所成角都是相等,要求截面面积最大,则截面的位置为夹在两个面与中间的,且过棱的中点的正六边形,且边长为,所以其面积为,故选A.点睛:该题考查的是有关平面被正方体所截得的截面多边形的面积问题,首要任务是需要先确定截面的位置,之后需要从题的条件中找寻相关的字眼,从而得到其为过六条棱的中点的正六边形,利用六边形的面积的求法,应用相关的公式求得结果.二、填空题:本题共4小题,每小题5分,共20分。
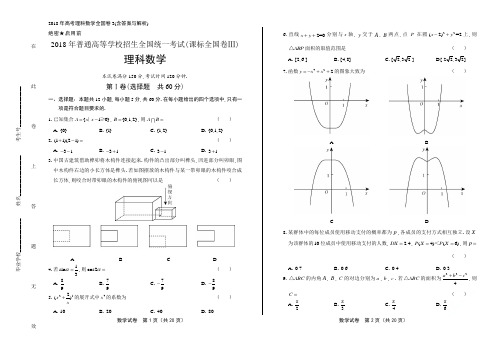
2018年高考理科数学全国卷3(含答案与解析) 数学试卷 第1页(共20页) 数学试卷 第2页(共20页)绝密★启用前2018年普通高等学校招生全国统一考试(课标全国卷Ⅲ)理科数学本试卷满分150分,考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{10}A x x =-∣≥,{0,1,2}B =,则A B = ( )A .{0}B .{1}C .{1,2}D .{0,1,2} 2.()(1i 2i)+-=( )A .3i --B .3i -+C .3i -D .3i +3.中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )ABC D 4.若1sin 3α=,则cos2α=( )A .89B .79C .79-D .89-5.252()x x+的展开式中4x 的系数为( )A .10B .20C .40D .806.直线2=0x y ++分别与x 轴,y 交于A ,B 两点,点P 在圆22(2)=2x y -+上,则ABP △面积的取值范围是( )A .[2,6 ]B .[4,8]C .[2,3 2 ]D [ 22,32] 7.函数422y x x =-++的图象大致为( )ABCD8.某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立.设X为该群体的10位成员中使用移动支付的人数, 2.4DX =,()6(4)P X P X ==<,则p =( )A .0.7B .0.6C .0.4D .0.39.ABC △的内角A ,B ,C 的对边分别为a ,b ,c .若ABC △的面积为2224,则C = ( )A .π2B .π3C .π4D .π6毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共20页) 数学试卷 第4页(共20页)10.设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为93,则三棱锥D ABC -体积的最大值为( )A .123B .183C .243D .54311.设1F ,2F 是双曲线C :22221(0,0)x y a b a b-=>>的左、右焦点,O 是坐标原点.过2F 作C 的一条渐近线的垂线,垂足为P .若1||6||PF OP =,则C 的离心率为 ( )A .5B .2C .3D .2 12.设0.2log 0.3a =,2log 0.3b =,则( )A .0a b ab +<<B .ab a b +<<0C .0a b ab +<<D .0ab a b +<<第Ⅱ卷(非选择题 共90分)二、填空题:本题共4小题,每小题5分,共20分.13.已知向量2)(1,=a ,)2(2,=-b ,),(1λ=c .若2()+∥c a b ,则=λ . 14.曲线)e (1xy ax =+在点(0,1)处的切线的斜率为2-,则a = .15函数π()cos(3)6f x x =+在[0,π]的零点个数为 .16.已知点1()1,M -和抛物线C :²4y x =,过C 的焦点且斜率为k 的直线与C 交于A ,B 两点.若90AMB ∠=,则k = .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.) (一)必考题:共60分. 17.(12分)等比数列{}n a 中,11a =,534a a =. (1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和.若63m S =,求m .18.(12分)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min )绘制了如下茎叶图:(1)根据茎叶图判断哪种生产方式的效率更高,并说明理由;(2)求40名工人完成生产任务所需时间的中位数m ,并将完成生产任务所需时间超过超过m不超过m第一种生产方式 第二种生产方式(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?附:22()(a b)(c d)(a c)(b d)n ad bc K -=++++,2()P K k ≥0.050 0.010 0.001k3.841 6.635 10.82819.(12分)-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------2018年高考理科数学全国卷3(含答案与解析)数学试卷 第5页(共20页) 数学试卷 第6页(共20页)如图,边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)当三棱锥M ABC -体积最大时,求面MAB 与面MCD 所成二面角的正弦值.20.(12分)已知斜率为k 的直线l 与椭圆C :22143x y +=交于A ,B 两点,线段AB 的中点为(1,)()M m m >0.(1)证明:12k <-;(2)设F 为C 的右焦点,P 为C 上一点,且0FP FA FB ++=.证明:FA ,FP ,FB成等差数列,并求该数列的公差. 21.(12分)已知函数22()()ln(1)2f x a x x x x +=-++.(1)若0a =,证明:当10x -<<时,()0f x <;当0x >时,()0f x >; (2)若=0x 是()f x 的极大值点,求a .(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.[选修4—4:坐标系与参数方程](10分)在平面直角坐标系xOy 中,O 的参数方程为cos ,sin x y θθ=⎧⎨=⎩(θ为参数),过点(0,2)且倾斜角为α的直线l 与O 交于A ,B 两点. (1)求α的取值范围;(2)求AB 中点P 的轨迹的参数方程.23.[选修4—5:不等式选讲](10分) 设函数()211f x x x =++-. (1)画出() y f x =的图象;(2)当[ 0),x ∈+∞,()b x f ax +≤,求a b +的最小值.毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共20页) 数学试卷 第8页(共20页)2018年普通高等学校招生全国统一考试(课标全国卷Ⅲ)理科数学答案解析第Ⅰ卷一、选择题 1.【答案】C【解析】∵={1}A x x |≥,{0,1,2}B =,∴={1,2}A B ,故选C .2.【答案】D【解析】21i 2i)(2i 2i i 3i )(+-=-+-=+,故选D . 3.【答案】A【解析】两个木构件咬合成长方体时,小长方体(榫头)完全嵌入带卯眼的木构件,易知俯视图可以为A .故选A . 4.【答案】B 【解析】由1sin 3α=,得22127cos212sin 12()=1=399αα=-=-⨯-.故选B .5.【答案】C【解析】252()x x+的展开式的通项251103155()(2)2r r r r r r r T C x x C x ---+==,令1034r -=,得2r =,所以4x 的系数为225240C ⨯=.故选C . 6.【答案】A【解析】由圆22(2)=2x y -+可得圆心坐标(2,0),半径r =ABP △的面积记为S ,点P 到直线AB 的距离记为d ,则有12S AB d =.易知AB =maxd ==min d =所以26S ≤≤,故选A .7.【答案】D【解析】∵42()2f x x x =-++,∴3()42f x x x '=-+,令()0f x '>,解得x <或x 0<此时,()f x 递增;令()0f x '<,解得x <0或x ,此时,()f x 递减.由此可得()f x 的大致图象.故选D . 8.【答案】B【解析】由题知~1()0,X B p ,则(101 2.4)DX p p =⨯⨯-=,解得0.4p =或0.6.又∵()6(4)P X P X ==<,即446664221010(1)(1)(1)0.5C P p C P p p p p --⇒-⇒<<>,∴0.6p =,故选B .9.【答案】C【解析】根据余弦定理得2222cos a b c ab C +-=,因为2224ABCa Sbc +-=△,所以c 42os ABC ab C S =△,又1sin 2ABC S ab C =△,所以tan 1C =,因为π()0,C ∈,所以4C π=.故选C .10.【答案】B【解析】设ABC △的边长为a ,则1sin60=932ABC S a a =△,解得6a =(负值舍去).ABC △的外接圆半径r 满足62sin60r=,得r =球心到平面ABC 的距离为2=.所以点D 到平面ABC 的最大距离为246+=,所以三棱锥DABC -体积的最大值为163⨯=故选B .11.【答案】C【解析】点2(,0)F c 到渐近线b y x a =的距离2(0)PF b b ==>,而2OF c =,所以在2Rt OPF △中,由勾股定理可得OP a ,所以1PF ==.在2Rt OPF △中,222cos PF b PF O OF c∠==,在12F F P△中,2222222121221246cos 22PF F F PF b c a PF O PF F F b c+-+-∠==⋅⋅2,所以222222463464b b c a b c a c bc +-=⇒=-,则有22223()46c a c a -=-值舍去),即e =.故选C .2018年高考理科数学全国卷3(含答案与解析)数学试卷 第9页(共20页) 数学试卷 第10页(共20页)12.【答案】B【解析】解法一:∵0.20.2log 0.3log 1=0a =>,22log 0.3log 1=0b =<,∴0ab <,排除C . ∵0.20.20log 0.3log 0.2=1<<,22log 0.3log 0.5=1-<,即01a <<,1b <-,∴0a b +<,排除D .∵220.2log 0.3lg0.2log 0.2log 0.3lg 2b a ===,∴2223log 0.3log 0.2log 12b b a -=-=<,∴1bb ab a b a+⇒+<<,排除A .故选B . 解法二:易知01a <<,1b -<,∴0ab <,0a b +<, ∵0.30.30.311log 0.2log 2log 0.41a b +=+=<, 即1a bab+<,∴a b ab +>, ∴0ab a b +<<.故选B .第Ⅱ卷二、填空题13.【答案】12【解析】由已知得2(4,2)+=a b .又,()1c λ=,2()+∥c a b ,所以42=0λ-,解得12λ=. 14.【答案】3-【解析】设(e ))1(x f x ax =+,则()()1e x f x ax a '=++,所以曲线在点(0,1)处的切线的斜率(0)12k f a '==+=-,解得3a =-. 15.【答案】3【解析】令()0f x =,得πcos(3)6x +,解得ππ+()39k x k =∈Z .当0k =时,π9x =;当1k =时,4π9x =;当2k =时,7π9x =,又[ 0,π]x ∈,所以满足要求的零点有3个.16.【答案】2【解析】解法一:由题意可知C 的焦点坐标为(1,0),所以过焦点(1,0),斜率为k 的直线方程为1y x k =+,设111,y A y k ⎛⎫+ ⎪⎝⎭,221,y B y k ⎛⎫+ ⎪⎝⎭,将直线方程与抛物线方程联立得21,4,y x k y x ⎧=+⎪⎨⎪=⎩整理得2440y y k --=,从而得124y y k +=,124y y =-.∵1()1,M -,90AMB ∠=,∴0MA MB =,即1212(2)(2)(1)(1)0y yy y k k+++--=,即2440k k -+=,解得2k =.解法二:设11A(,)x y ,22(),B x y ,则2112224,4,y x y x ⎧=⎨=⎩①②②-①得2221214()y y x x -=-,从而2121124y y x x k y y --+==.设AB 的中点为M ',连接MM '.∵直线AB 过抛物线24y x =的焦点,∴以线段AB 为直径的M '⊙与准线:1l x =-相切.∵1()1,M -,90AMB ∠=,∴点M 在准线:1l x =-上,同时在M '⊙上,∴准线l 是M '⊙的切线,切点M ,且MM l '⊥,即MM '与x 轴平行,∴点M '的纵坐标为1,即1212221y y y y =⇒++=,故124422y y k =+==. 故答案为:2. 三、解答题17.【答案】(1)解:设{}n a 的公比为q ,由题设得1n n a q -=.由已知得424q q =,解得0q =(舍去)或2q =-或2q =. 故1(2)n n a -=-或12n n a -=. (2)若1(2)n n a -=-,则1(2)3nn S --=.数学试卷 第11页(共20页) 数学试卷 第12页(共20页)由63m S =得(2)188m -=-.此方程没有正整数解.若12n n a -=,则21n n S =-.由63m S =得264m =,解得6m =. 综上,6m =.【解析】(1)解:设{}n a 的公比为q ,由题设得1n n a q-=.由已知得424q q =,解得0q =(舍去)或2q =-或2q =. 故1(2)n n a -=-或12n n a -=.(2)若1(2)n n a -=-,则1(2)3n n S --=.由63m S =得(2)188m -=-。

2017—2018学年度高三第三次调研测试理科数学本试卷共23小题,共150分,共6页,考试时间120分钟,考试结束后,将答题卡和试题卷一并交回。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条 形码、姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案 的标号;非选择题答案必须使用0.5毫米黑色字迹的签字笔书写,字体工整、 笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案 无效。
4. 作图可先用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5. 保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮 纸刀。
一、选择题:本大题共12题,每小题5分,共60分,在每小题给出的四个选项中,只有一个是符合题目要求。
1. 若集合{|0}B x x =≥,且A B A =,则集合A 可以是A .{1,2}B .{|1}x x ≤C .{1,0,1}-D .R2. 已知复数1z i =+(i 为虚数单位)给出下列命题:①||z =;②1z i =-;③z 的虚部为i . 其中正确命题的个数是A. 0B. 1C. 2D. 33. 若1sin ,3α=且2παπ<<,则sin 2α=A .B .C .D . 4. 已知等差数列{}n a 的公差不为0,11a =,且248,,a a a 成等比数列,设{}n a 的前n 项和为n S ,则n S =A. (1)2n n +B. 2(1)2n +C. 212n + D. (3)4n n +5. 若1()n x x-的展开式中只有第7项的二项式系数最大,则展开式中含2x 项的系数是A . 462-B . 462C . 792D . 792-6. 执行如图所示的程序框图,输出的S 值为 A.12018B. 12019C. 20172018D. 201820197. 10|1|x dx -=⎰A .12B . 1C . 2D . 38. 一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是 (0,0,0),(1,0,1),(0,1,1)1,(,1,0)2,绘制该四面体三视图时,按照如图所示的方向画正视图,则得到左视图可以为 A.B.C.D.9. 设曲线()cos (*)f x m xm R =∈上任一点(,)x y 处切线斜率为()g x ,则函数2()y x g x =的部分图象可以为10.平行四边形ABCD 中,2,1,1,AB AD AB AD ===-点M 在边CD 上,则MA MB 的 最大值为A. 2B. 1C. 5D.111. 等比数列{}n a 的首项为32,公比为12-,前n 项和为n S ,则当*n N ∈时,1n nS S -的最 大值与最小值的比值为A. 125-B. 107- C. 109D.12512.已知函数13,1()22ln ,1x x f x x x ⎧+≤⎪=⎨⎪>⎩(ln x 是以e 为底的自然对数, 2.71828e =),若存在实数,()m n m n <,满足()()f m f n =,则n m -的取值范围为 A. 2(0,3)e +B. 2(4,1]e -C. 2[52ln2,1]e --D. [52ln2,4)-二、填空题:本大题共4个小题,每小题5分。

2018年全国统一高考数学试卷(理科)(新课标Ⅰ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)设z=+2i,则|z|=()A.0B.C.1D.2.(5分)已知集合A={x|x2﹣x﹣2>0},则∁R A=()A.{x|﹣1<x<2}B.{x|﹣1≤x≤2}C.{x|x<﹣1}∪{x|x>2}D.{x|x≤﹣1}∪{x|x≥2}3.(5分)某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是()A.新农村建设后,种植收入减少B.新农村建设后,其他收入增加了一倍以上C.新农村建设后,养殖收入增加了一倍D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4.(5分)记S n为等差数列{a n}的前n项和.若3S3=S2+S4,a1=2,则a5=()A.﹣12B.﹣10C.10D.125.(5分)设函数f(x)=x3+(a﹣1)x2+ax.若f(x)为奇函数,则曲线y=f(x)在点(0,0)处的切线方程为()A.y=﹣2x B.y=﹣x C.y=2x D.y=x6.(5分)在△ABC中,AD为BC边上的中线,E为AD的中点,则=()A.﹣B.﹣C.+D.+7.(5分)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.2B.2C.3D.28.(5分)设抛物线C:y2=4x的焦点为F,过点(﹣2,0)且斜率为的直线与C交于M,N两点,则•=()A.5B.6C.7D.89.(5分)已知函数f(x)=,g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是()A.[﹣1,0)B.[0,+∞)C.[﹣1,+∞)D.[1,+∞)10.(5分)如图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.△ABC的三边所围成的区域记为I,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p1,p2,p3,则()A.p1=p2B.p1=p3C.p2=p3D.p1=p2+p3 11.(5分)已知双曲线C:﹣y2=1,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M,N.若△OMN为直角三角形,则|MN|=()A.B.3C.2D.412.(5分)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。

长春市普通高中20怡届高三质量监测(三〉数学试题卷(理科)耆生硕知: t 各试空分试聰砂答題卡,構分150井,石试时间】20分钟.2. 淬聴乩 在斟SF 抬宼位据匕境写学检.班纽 社名和准警证号.3. 希有答案必皱耳在务朗左上,打龙试总上无效. 4号试黠忆 製需上殳界轉卡一一、谨择題:本鏈共M 小题,每小眩空井"吞每小赵给出的四个选项中、只商一项是符 合题目毀滾的一 (t > 设集 fr.l^{x||x|<l), B = {x\x(x-3)<U}.刪 dURz(A)卜IQ U) (0.1)(C) (-13><D> (1,3)(2> 若埶数工=则|=|=[-i迅行运兀跑的摆辿們式仃纵横:老种瞄 式(如图所示).如吟松位数时*輝阿拉时汁数 样.把朴牛数旳的数码从圧到右抑列,«H 他栽码的序式胡徑覘* 釧町 个仏 百肯、力中t [网做虫 紬粘卜位.丁世・十万何用槌式展叮;•以 此芟他 例俎H66用S7并盂小祖肚二II 丄「刚翳71用券尊可劇为 2 占丄 Tl (B) HT X X I (C) i T± ■ (D> TIT 丄 1F_J5)榔ift 眈/(.¥)'Sin(2.i h 3)的用傑向f I T ft <J 个讯位曙f i!函数耳(灯二COS 2x 的 r 3 牌傑.測凸的ffl 诃门打;T S JT1 1,7 1?肚 l A )一 CID 二 fC>心—— 12J2 12 12 数学试独艸科〉 詭1贞(搖4就)(B) 0CD)迈(3) 中国有个名旬“运磬桂犍Z 中.决胖『咐之外■・其中的“溥”療您赴描<*hf P 经)中记朝的算靜.古代川订为廉址行计 ■ KSA#几寸长的小竹棍摆机平血LI II 01 Illi hli T T nr >± X = ms痢数 /(x) = l + /+—为til 图所不程用Hi 图是为r 求出满足2"-^ >28抑扯小偶 如、那么唯白框中的迥旬及巌后输岀的”悄分別是(A) n = n + l ^1 6(BJ M = “ + 2和 6 (CJ H = rt 4-1 S (D) n = n + 2^ml_«j(7} (T 本用间的W 摆放在恪架时同一栏上「變求屮、乙第本肝必坝摆做张幅攔• W* 丁两点书謝须相邻,则小岡的建旗方汎有I )种.(A) 24CB )36 «:1 48(8> 某几何縊的 濒用如图所同;(单册cm ),则劇L 何体的体扔E 帕趴cm >是<A) 4^3 〔B 〉罗厉(C )2血 (D)語(9) LABlA^flC 的内的对边分别为,b * Ci 齐 2/fttwi /?兰fjgs ( + c ix>s A・ h-2 ・则△屛賦曲 紂的城人Fi 圧<M I⑹ J3 <C)2(D )4(IQ) |2扫1边怏为2的竽追決形MC ・0为肚的中点・以』£>为析腿将4仏「 折诫zm, ant 凡乩GDIB 点的球的泯面机为 (A) 2JT口昇 M(C) 4ffCD)Ml) 口甜悠曲线三-亠 "的左后柄忙建点仃劭为幷利巧•种儿和支卜一存症一nr rtv -\点尸淌址丹;丄怦;,何冷△丹•出的圍舉为L 则谀取曲冀的禺心率为(A)—【1口 — <C> 2 <Di 32 2(12)已知定又域为H 的甫H/QO 的用乂择ii 点亿I),H 对*wR ,都有 广⑴八2. /(1QU 313T -11) < 3- log 7;: | T 为CA )似心) &B )(-oo,0}U<OJ) (C) Y 」)3 (-LO>U(0J)G'r 试趣连t 理斟】 苹2 1「人4 i ;CSC' -1A =2" ft'訂/畔上/二、填空砸:本SLh 4小題,旬小趣5分.“0(IJ)设实fltxj需足釣束策林・4一丫一$心0*聊二二” + 2y們最大值为x + V 5L °i456y口m涯Ift点圈井折町知=y』』x找性机羌. 为㈱确fjo.i),畠/(盘)耳2,则实数“的联恒盘国虽lag, Jr J:>O P(15)(15)乜殛长为2的弄蝮白柳△#放屮…讨为斜边/R的屮0,点P为该平记内-动啟苦冈卜2・M(S4'PS + 4XPC*/*A7)的眾小值屋______________•三、解答麵:共期分解答应舄生女字说明、证明过程或演算歩骤一第17-21掘为必考建, 毎个试强考生都叠须作答.第2篁苗趣为选考题*考生根揣要求件答•<-)必考题:共60分.(17)Ct耶题満分俺和仪进列{叫}的4沖项和为乙+吐忆二用",在正项巒说戳列{和也爲-吋(1)求{叫}和仏讣的期琨企式;< JD址1打二务求麹列{□}的li沏顶和匚-(18)(本小题満分门分)树立和躅行41録朮育山就是金血阚山・甲排人与自然和躅共牛"'射理念越来拯怎入人心.已圧威了全代门応穆叮*造祖方41的肚性劭环一据此旅H站推! 11T关严卞奁文明翅设进展愴况的确杳.大凰的蟒计截霍憲明・雾与谓査舟中关注此问趣的约占闕需刀!从需与调査的人郡中册应出200人■笄谒这200人按年岭分第I 组P5J5),閉2 ^{25,35).谊J犯[3翼45)「第4疑[4畀55)・笫3姐[5黑祐“再到的频率分布口方團如團所示i< \)求左的th(ri)現在熨从年龄鞍小的第b 2t 3蛆中用务层抽样的方世抽胞门人・再从这门人中樂机抽取J人迥订何卷英許・求在f I组巴帔拯到[人的刑覆F.^3 坦褫扯到2人的魄率;(IU)苕从所有参与调査的人中址意选出J A-记关注"诜丈明”的人数为片I 求X的分布対与期卑.灶学试軀隹f;T i!h u:(K- 4 )(旳〉(:本小题満分门分)在如图瞬示的儿忖悴屮,PA.1平面A BCD t E.F卧訓杲im AD, PH的中点・PA -AB = \(I)求证:EF#平面DO1;(II j求平面EFX7与平面/YX?所或锐二面角的金径值.rio> {本小题満分M分)托平删倒处坐栋承4 E油【関q的方用为"7口於虫・阀匚的方程^(i+ty+Z^b动岡卍与BIG内切切.< [)诜动訂関心厂的比迹E的厅楼:(ID巴知理-2』)制02,(1}为甲面内的两个宦点*过(14)点的氏战丿与轨迹E空于川』B两点、求0ii® APBQ的鈕大值.CD (本小趣滿分订労)已知隅議/"(工)冃”-4工*5-耳,(1〕若/'(刃在R上垦单魁递增喀咯求"的取遠范凤(It) ^g(T)-^/(X).当Q1时.若竄斗)乜(对"童(冊卜眞中^! < ftf < Jj -求i吐Jf t + x2< 2m(-)進考降垄】0处请考生在22、工3题中任选一题柞答一如果务傩*则按所做的第一12计*<22)(本申題満分苗分)选^4-4:坐标系与参賞方程选讲在氏期坐标JfiQ巾.以坐悔亂虫为楼血,X轴正半输为极挡建宜极劭标氛*曲啦;:"畑話— R「“如?"H )求G弓匚;交点的極磋标;〔II)设点a在G」:・觅=亍囲・欢动点尸的极坐标方翟(23)(本小麓潘分4份)选捲1黛不等武逸讲己知函数f (工)=|纠*|2x*3| + m・meR.〔I )当耐=—2时.求不等式/(i)^3的解能:£ [[)讨卜滋F(F,0h都有一广(工)$工+二怔戍立+求椭的眾值施阴■耽学试啦養!呷孑门第斗旬{扛4亟)长春市普通高中2018届高三质量监测(三)数学(理科)试题参考答案及评分标准一、选择题(本大题共 12小题,每小题5分,共60分) 1. C 2. A 3. C4. D5.C6. D7. A8. B9. B10. D11. B12. B简答与提示: 1. 【命题意图】本题考查集合的运算 .【试题解析】C A 二{x| -1 ::: x ::: 1}, B 二{ x| 0 ::: x :: 3}, AUB =(一1,3).故选 C. 2. 【命题意图】本题考查复数 . 【试题解析】A z =i,|z|=1.故选A.3. 【命题意图】本题考查中华传统文化中的数学问题 . 【试题解析】C 由算筹含义.故选C.4.【命题意图】本题主要考查函数的图象及性质【试题解析】D 由函数是偶函数,排除 A ,C ,当x ・(0, —),tanx .0.故选D.25.【命题意图】本题考查三角函数的相关知识 .【试题解析】C 由题意知,a = -一 • k 二,k • Z .故选C.126. 【命题意图】本题主要考查算法的相关知识 . 【试题解析】D 根据程序框图.故选 D7.【命题意图】本题考查计数原理的应用 . 【试题解析】A 由题意知A 2A 3A ; =24.故选A.8.【命题意图】本题主要考查三视图问题 .【试题解析】B 由题意可知该几何体为正三棱柱去掉一个小三棱锥,12. 【命题意图】本题是考查导数在研究函数单调性上的应用【试题解析】B 令F(x) = f(x)+2x ,有L(x)=f(x 七 刃,所以F(x)在定义域内 单调递增,由 f(1)=1,得 F® =f) 2 3 ,因为 f(log 2 |3x —1|) v3—log 出 |3x —1|9.V=4E 」2G 」°W .故选B.3 3【命题意图】本题主要考查解三角形的相关知识 .【试题解析】B 由题意知B=60,由余弦定理,2ac =a2c 一 4 — 2ac - 4,有 ac 空 4,故 S2 2ac = a c - 4,故1acsin B 乞、3 .故选 B.210.11.【命题意图】本题主要考查球的相关问题 .【试题解析】 D 折后的图形可放到一个长方体中,其体对角线长为 故其外接球的半径为 5,其表面积为2【命题意图】本题考查双曲线的相关知识 1+1+3二、一 5,5二.故选D.【试题解析】B 由双曲线可知S PFF=m 2-1 = 3,m 2= 4,从而』.故选B.2等价于 f (log 2|3x -1|) 2log 2|3x -1|:::3,令 t=log 2|3x -1|,有 f (t ) 2t :::3,则有t :1,即 log 2 |3x-1| :::1,从而 0 :::| 3x _ 1| ::: 2,解得 x :: 1,且 x 严 0.故选 B. 二、填空题(本大题共 4小题,每小题5分,共20分)13. 9 14. 1.715. (_::,_1]U[4, ::) 16. 48-32、、2简答与提示: 13. 【命题意图】本题考查线性规划问题 . 【试题解析】由可行域可确定目标函数在 (1,4)处取最大值9.14.【命题意图】本题考查回归方程的相关知识.【试题解析】将 x=3.2代入回归方程为y? = x ・1可得y -4.2,贝U 4m = 6.7 , 解得m= 1.675,即精确到0.1后m 的值约1.7. 15. 【命题意图】本题考查分段函数的相关知识1【试题解析】当X _0,(—)x_2,x _-1,当x 0 竄_4x_,故(::〒]4lh : .216. 【命题意图】本题考查平面向量的相关知识 【试题解析】由题意可知其最小值为48 - 32-、2.三、解答题17. (本小题满分12分)【命题意图】本题考查数列的基本方法及数列求和2【试题解析】解:(1) Q S n = n 2 -n ,令n =1 , q =0a . =Sn -S n 」=2 n -1 , n — 2a n =2 n-1 又 Q 数列仏?为等比,b 2 二 a 2=2 , b 4 二 a 5=8—=q = 4,又各项均为正• q = 2 , - bn = 2°4b 2(2)由(1)得:c n 二 n-1 -2nT n =0 2-1 23-1 23 L n-12n=1 222 23L n-1 2n2T n 二 1 232 24Ln - 2 2n n-1 2n 1-T n =222324L 2n - n-1 2n 1T n = n -2 2n 14 18. (本小题满分12分)【命题意图】本小题主要考查学生对频率分布直方图的理解以及分布列的相关知识 【试题解析】解:(1)由 10 0.010 0.015 a 0.030 0.010 =1,得 a = 0.035,(2)第1, 2, 3组的人数分别为20人,30人,70人,从第1, 2, 3组中用分层抽样的 方法抽取12人,则第1 , 2, 3组抽取的人数分别为 2人,3人,7人.设从12人中随机抽取3人,第1组已被抽到1人为事件A ,第3组抽到2人为事件B ,汁""1尹 1-2n 1n 1=2-n-12-4C ;CP AB G 32P(A) " C2C1O - C |C ;0C 2则 P B|A 二21 50(3)从所有参与调查的人中任意选出4概率为P , X 的可能取值为0,54 3 1.P X =0 二咖--)3:5 125 1人,关注“生态文明”的 1,2, 3.14 1 4 2 12Px" 话 19. 2 4 2 4 1 48 343P X =2 二C 3(y (1-匸) ,P X =3 二C 3(匚) 5 5 125 5想象能力、推理论证能力和运算求解能力 • 【试题解析】答案:(1 )取PC 中点M ,连接DM ,MF64 125本题考查学生的空间1丁 M ,F 分别是 PC, PB 中点,二 MF 〃CB MF =^CB ,, 21E 为 DA 中点,ABCD 为矩形,.DE/CB’DE -^CB ,2.MF // DE, MF = DE ,.四边形DEFM 为平行四边形.EF // DM , EF -平面 PDC , DM 二平面 PDC ,. EF // 平面 RDC(2PA_平面ABC ,且四边形 ABCD 是正方形,.AD, AB, AP 两两垂直, 原点,AP AB AD x, y, z A-xyz 则 P 1,0,0 , D 0,0,1,C 0,1,1, E(0,0,设平面EFC 法向量为m =(x, y,z),1 1 1;),F(;,;,°) 2 2 21 1 11 1 EF 十,,),FC =(, ,1)EF n = 0则一11,取 m = 3,-1,2y z = 0召2 T T则设平面 PDC 法向量为 n 2=(x,y,z), PD= (-1,0,1),PC =(-1,1,1),即 \FC n =0PD n 2 PC n 2 4 T cos : n 1,=0 -0_ x + z = 0 -* 「x + y + z = 0,取宀1。

2018年吉林省长春市高考数学三模试卷(文科)含解析2018年吉林省长春市高考数学三模试卷(文科)一、选择题(本大题包括12小题,每小题5分,共60分。
每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项涂在答题卡上)1.已知复数z=1+2i,则z²+4z+3的值为()。
A.5 B.5+4i C.-3 D.3-4i2.已知集合A={x|x²-2x-3<0},B={x||x|<2},则A∩B=()。
A.{x|-2<x<2} B.{x|-2<x<3} C.{x|-1<x<3} D.{x|-1<x<2}3.设a,b均为实数,则“a>|b|”是“a³>|b|³”的()。
A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件4.直线x-3y+3=0与圆(x-1)²+(y-3)²=10相交所得弦长为()。
A.√5 B.2√5 C.4 D.35.下列命题中错误的是()。
A.如果平面α外的直线a不平行于平面α,则内不存在与a平行的直线。
B.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么直线l⊥平面γ。
C.如果平面α⊥平面β,则平面α内所有直线都垂直于平面β。
D.一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交。
6.在平面内的动点(x,y)满足不等式|x+2|+|y-1|≤5,则z=2x+y的最大值是()。
A.-4 B.4 C.-2 D.27.某几何体的三视图如图所示,则其体积为()。
A.4 B.8 C.16 D.328.某高中体育小组共有男生24人,其50m跑成绩记作ai(i=1,2,…,24),若成绩小于6.8s为达标,则如图所示的程序框图的功能是()。
A.求24名男生的达标率 B.求24名男生的不达标率C.求24名男生的达标人数 D.求24名男生的不达标人数9.等比数列{an}中各项均为正数,Sn是其前n项和,且满足2S3=8a1+3a2,a4=16,则S4=()。
2018 年一般高等学校招生全国一致考试( Ⅰ卷 )文科数学注意事项:1.答卷前,考生务势必自己的九名、考生号等填写在答题卡和试卷指定地点上.2.回答选择题时,选出每题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需变动,用橡皮擦洁净后,再选涂其余答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题(此题共 12 小题,每题 5 分,共60 分.在每题给出的四个选项中,只有一项是切合题目要求的.)1.已知会合 A 0,2 ,B 2 , 1,0 ,1,2 ,则AIB ()A. 0,2 B. 1,2 C. 0 D. 2, 1,0 ,1,21 i,则 z ()2.设z 2i1 iA.0 B.1C. 1 D. 2 23.某地域经过一年的新乡村建设,乡村的经济收入增添了一倍.实现翻番.为更好地认识该地域乡村的经济收入变化状况,统计了该地域新乡村建设前后乡村的经济收入组成比率.获得以下饼图:则下边结论中不正确的选项是()A.新乡村建设后,栽种收入减少B.新乡村建设后,其余收入增添了一倍以上C.新乡村建设后,养殖收入增添了一倍D.新乡村建设后,养殖收入与第三家产收入的总和超出了经济收入的一半4.记 S n为等差数列a n的前n项和.若 3S3 S2 S4, a1 2 ,则 a3 ()A.12 B.10 C.10 D. 125.设函数 f x x 3a 1 x 2ax .若 f x 为奇函数, 则曲线 yf x 在点 0 ,0 处的切线方程为()A . y2xB . y xC . y 2xD . y x6.在 △ ABC 中, AD 为 BC 边上的中线,uuurE 为 AD 的中点,则 EB ()A . 3 uuur1 uuurB . 1 uuur 3 uuur4 AB4 AC 4 AB AC4 C . 3 uuur 1 uuur D . 1 uuur 3 uuur 4 AB4 AC4 AB AC47.某圆柱的高为 2,底面周长为 16,其三视图以下图,圆柱表面上的点 M 在正视图上的对应点为 A ,圆柱表面上的点 N 在左视图上的对应点为 B ,则在此圆柱 侧面上,从 M 到 N的路径中,最短路径的长度为( )A .2 17B .2 5C .3D .28.设抛物线 C :y24 x 的焦点为 F ,过点2 ,0 且斜率为2的直线与 C 交于 M , N 两点,3uuuur uuur ()则FM FNA .5B . 6C .7D . 89.已知函数 f xx, ≤0 , f xf x x a (),若 g x 存在 2 个零点, 则 a 的exln x ,x 0取值范围是A . 1,0B . ,C . 1,D . 1,10.下列图来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆组成,三个半圆的直径分别为直角三角形ABC 的斜边 BC ,直角边 AB , AC , △ ABC 的三边所围成的地区记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ,在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p 1 , p 2 , p 3 ,则( )A . p 1 p 2B . p 1 p 3C . p 2 p 3D . p 1 p 2p 3211.已知双曲线 C :xy 2 1 , O 为坐标原点, F 为 C 的右焦点,过 F 的直线与 C 的两条渐 3近线的交点分别为 M , N .若 △ OMN 为直角三角形,则 MN () A .3B . 3C .2 3D . 4212.设函数 f x2 x, ≤ 0,则知足 f x 1f 2x 的 x 的取值范围是()x 01,yA .,1B . 0,C . 1,0D . ,0二、填空题(此题共 4 小题,每题 5 分,共 20 分)13.已知函数 f xlog 2 x 2 a ,若 f 31 ,则 a________.x 2 y 2 ≤ 014.若 x ,y 知足拘束条件x ≥ 0 ,则 z3x 2 y 的最大值为 ________.y 1y ≤ 015.直线 y x 1 与圆 x 2y 2 2 y 3 0 交于 A ,B 两点,则 AB________ .16. △ ABC 的内角 A ,B ,C 的对边分别为 a ,b ,c ,已知 b sinC csin B4asin Bsin C ,b 2c 2 a 2 8 ,则 △ ABC 的面积为 ________.三、解答题(共70 分。
长春市普通高中2018届高三质量监测(三)数学(理科)试题参考答案及评分标准一、选择题(本大题共12小题,每小题5分,共60分)1. C2. A3. C4. D5.C6. D7. A8. B9. B 10. D 11. B 12. B简答与提示:1. 【命题意图】本题考查集合的运算. 【试题解析】C {|11},{|03},(1,3)A x x B x x A B =-<<=<<=-U .故选C.2. 【命题意图】本题考查复数.【试题解析】A ,||1z i z ==.故选A.3. 【命题意图】本题考查中华传统文化中的数学问题.【试题解析】C 由算筹含义. 故选C.4. 【命题意图】本题主要考查函数的图象及性质.【试题解析】D 由函数是偶函数,排除A ,C ,当(0,)2x π∈,tan 0x >.故选D.5. 【命题意图】本题考查三角函数的相关知识.【试题解析】C 由题意知,,12a k k ππ=-+∈Z .故选C.6. 【命题意图】本题主要考查算法的相关知识.【试题解析】D 根据程序框图.故选 D 7. 【命题意图】本题考查计数原理的应用.【试题解析】A 由题意知23223224A A A =.故选A.8. 【命题意图】本题主要考查三视图问题.【试题解析】B 由题意可知该几何体为正三棱柱去掉一个小三棱锥,123V =⋅=故选B.9. 【命题意图】本题主要考查解三角形的相关知识.【试题解析】B 由题意知60B =︒,由余弦定理,224ac a c =+-,故22424ac a c ac =+-≥-,有4ac ≤,故1sin 2ABC S ac B ∆=≤故选B. 10. 【命题意图】本题主要考查球的相关问题.【试题解析】D 折后的图形可放到一个长方体中,其体对角线长为,5π.故选D. 11. 【命题意图】本题考查双曲线的相关知识.【试题解析】B 由双曲线可知122213,4PF F S m m ∆=-==,从而2e =.故选B.12. 【命题意图】本题是考查导数在研究函数单调性上的应用.【试题解析】B 令()()2=+F x f x x ,有()()20''=+>F x f x ,所以()F x 在定义域内单调递增,由1)1(=f ,得(1)(1)23=+=F f ,因为2(log |31|)3|31|-<--x x f 等价于22(log |31|)2log |31|3-+-<x x f ,令2log |31|=-x t ,有()23+<f t t ,则有1<t ,即2log |31|1-<x ,从而0|31|2x<-<,解得1,<x 且0≠x . 故选B. 二、填空题(本大题共4小题,每小题5分,共20分)13. 9 14. 1.7 15. (,1][4,)-∞-+∞U16. 48-简答与提示:13. 【命题意图】本题考查线性规划问题.【试题解析】由可行域可确定目标函数在(1,4)处取最大值9. 14. 【命题意图】本题考查回归方程的相关知识.【试题解析】将 3.2x =代入回归方程为ˆ1yx =+可得 4.2y =,则4 6.7m =, 解得 1.675m =,即精确到0.1后m 的值约1.7.15. 【命题意图】本题考查分段函数的相关知识.【试题解析】当10,()2,12x x x ≤≥≤-,当20,log 2,4x x x >≥≥,故(,1][4,)-∞-+∞U .16. 【命题意图】本题考查平面向量的相关知识. 【试题解析】由题意可知其最小值为48-三、解答题17. (本小题满分12分)【命题意图】本题考查数列的基本方法及数列求和. 【试题解析】解:(1)Q 2n S n n =-,∴令1n =,10a =()121n n n a S S n -=-=-,()2n ≥∴()21n a n =- 又Q 数列{}n b 为等比,222b a ==,458b a == ∴2424bq b ==,又各项均为正∴2q =,∴12n n b -= (2)由(1)得:()12nn c n =-⋅∴()()()23021231212n n T n =+-⋅+-⋅++-⋅L ()23122212n n =⋅+⋅++-⋅L()()341212222212n n n T n n +=⋅+⋅++-⋅+-⋅L()2341222212n n n T n +-=++++--⋅L()()2112121212n n n -+-=--⋅-()112124n n n ++=--⋅-∴()1224n n T n +=-⋅+18. (本小题满分12分)【命题意图】本小题主要考查学生对频率分布直方图的理解以及分布列的相关知识.【试题解析】解:(1)由()100.0100.0150.0300.0101a ⨯++++=,得0.035a =, (2)第1,2,3组的人数分别为20人,30人,70人,从第1,2,3组中用分层抽样的方法抽取12人,则第1,2,3组抽取的人数分别为2人,3人,7人.设从12人中随机抽取3人,第1组已被抽到1人为事件A ,第3组抽到2人为事件B ,则()()1227312122121021031221|.()50C C P AB C P B A C C C C P A C ===+(3)从所有参与调查的人中任意选出1人,关注“生态文明”的概率为4,5P =X 的可能取值为0,1,2,3. ()033410(1)5125P X C ∴==-=,()112344121()(1)55125P X C ==-=()221344482()(1)55125P X C ==-=,()3334643()5125P X C ===~(3,)5X B Q ,()3.55E X np ==⨯=19. (本小题满分12分)【命题意图】本小题以四棱锥为载体,考查立体几何的基础知识. 本题考查学生的空间想象能力、推理论证能力和运算求解能力. 【试题解析】答案:(1)取PC 中点M ,连接MF DM , F M ,Θ分别是PB PC ,中点, CB MF CB MF 21,//=∴,E Θ为DA 中点,ABCD 为矩形,CB DE CB DE 21,//=∴,DE MF DE MF =∴,//,∴四边形DEFM 为平行四边形⊄∴EF DM EF Θ,//平面PDC ,⊂DM 平面PDC ,//EF ∴平面RDC(2)⊥PA Θ平面ABC ,且四边形ABCD 是正方形,AP AB AD ,,∴两两垂直,以A 为原点,AP ,AB ,AD 所在直线为z y x ,,轴,建立空间直角坐标系xyz A -则(),0,0,1P ()(),1,1,0,1,0,0C D 111(0,0,),(,,0)222E F设平面EFC 法向量为1(,,)n x y z =u r ,111(,,)222EF =-u u u r ,11(,,1)22FC =-u u u r则⎪⎩⎪⎨⎧=⋅=⋅0011n FC n EF , 即⎪⎩⎪⎨⎧=++-=-+021210z y x z y x ,取()2,1,31-=n 则设平面PDC 法向量为2(,,)n x y z =u u r ,(1,0,1)PD =-u u u r ,(1,1,1)PC =-uu u r则⎪⎩⎪⎨⎧=⋅=⋅0022n n , 即⎩⎨⎧=++-=+-00z y x z x , 取()1,0,12=n 121212311021cos ,14||||n n n n n n ⨯+-⨯+⨯⋅<>===⋅u r u u ru r u u r u r u u r .∴平面EFC 与平面PDC 所成锐二面角的余弦值为1475. 20. (本小题满分12分)【命题意图】本小题考查椭圆的标准方程及直线与椭圆的位置关系,考查学生的逻 辑思维能力和运算求解能力. 【试题解析】解:(1)设动圆C 的半径为r ,由题意知12||3,||1CC r CC r =-=+从而有12||||4CC CC +=,故轨迹E 为以12,C C 为焦点,长轴长为4的椭圆,并去 除点(2,0)-,从而轨迹E 的方程为221(2)43x y x +=≠-. (2)设l 的方程为1x my =+,联立221431x y x my ⎧+=⎪⎨⎪=+⎩, 消去x 得22(34)690m y mx ++-=,设点1122(,),(,)A x y B x y ,有12122269,,3434m y y y y m m --+==++则2212(1)||34m AB m +==+, 点(2,0)P -到直线l(2,0)Q 到直线l从而四边形APBQ的面积222112(1)23434m S m m +=⨯=++令1t t =≥,有224241313t S t t t==++,函数13y t t =+在[1,)+∞上单调递增, 有134t t +≥,故2242461313t S t t t==≤++,即四边形APBQ 面积的最大值为6.21. (本小题满分12分)【命题意图】本小题主要考查函数与导数的相关知识,以导数为工具研究函数的方法,考查学生解决问题的综合能力. 【试题解析】解:(1)Q ()f x 的定义域为x R ∈且单调递增,∴在x R ∈上,()240x af x x e'=-+≥恒成立,即:(42)x a x e ≥- ∴设()(42)x h x x e =- x R ∈ ,∴()(22)x h x x e '=-,∴当(,1)x ∈-∞时()0h x '>,∴()h x 在(,1)x ∈-∞上为增函数, ∴当[1,)x ∈+∞时()0h x '≤,∴()h x 在[1,)x ∈+∞上为减函数,∴max ()(1)2h x h e == Q max [(42)]x a x e ≥-,∴2a e ≥,即[2,)a e ∈+∞ .(2)Q ()()()245xxg x e f x x x e a ==-+-Q ()()()122g x g x g m += [)1,m ∈+∞,∴()()()12222112245452452x x m x x e a x x e a m m e a -+-+-+-=-+- ∴()()()1222211224545245x x m x x e x x e m m e -++-+=-+∴设()()245x x x x e ϕ=-+ x R ∈,则()()()122x x m ϕϕϕ+=, ∴()()210x x x e ϕ'=-≥ ∴()x ϕ在x R ∈上递增且()10ϕ'=令()1,x m ∈-∞,()2,x m ∈+∞∴设()()()F x m x m x ϕϕ=++-,()0,x ∈+∞∴()()()2211m x m x F x m x e m x e +-'=+----Q 0x > ∴0m x m x e e +->>,()()()22112220m x m x m x +----=-≥∴()0F x '≥,()F x 在()0,x ∈+∞上递增, ∴()()()02F x F m ϕ>=,∴()()()2m x m x m ϕϕϕ++->,()0,x ∈+∞,令1x m x =-∴()()()112m m x m m x m ϕϕϕ+-+-+>即:()()()1122m x x m ϕϕϕ-+>又Q 12()()2()x x m ϕϕϕ+=,∴()()()()12222m x m x m ϕϕϕϕ-+->即:()()122m x x ϕϕ->Q 1x m <,2x m >∴12m x m ->, Q ()x ϕ在x R ∈上递增∴122m x x ->,即:122x x m +<,得证.22. (本小题满分10分)【命题意图】本小题主要考查极坐标系与参数方程的相关知识,本小题考查考生的方程思想与数形结合思想,对运算求解能力有一定要求. 【试题解析】 (1)联立⎩⎨⎧==θρθρcos 43cos ,23cos ±=θ,20πθ<≤Θ,6πθ=,32=ρ交点坐标)6π.(2)设()θρ,P ,()00,θρQ 且.cos 400θρ=0[0,)2πθ∈,由已知,32QP OQ =得⎪⎩⎪⎨⎧==θθρρ0052θρcos 452=∴,点P 的极坐标方程为10cos ,[0,)2πρθθ=∈.23. (本小题满分10分)【命题意图】本小题主要考查不等式的相关知识,具体涉及到绝对值不等式解法等内容. 本小题重点考查化归与转化思想.【试题解析】(1)当2m =-时,()41(0)32232=1(0)2345()2x x f x x x x x x ⎧+≥⎪⎪⎪=++--⎨⎪⎪--≤-⎪⎩<<当4130x x +≤⎧⎨≥⎩解得12x ≤≤0;当30132x -≤<<,恒成立.当45332x x --≤⎧⎪⎨≤-⎪⎩解得322x -≤≤-,此不等式的解集为1[2]2-,.()43+(0)3223=3(0)2343()2x m x f x x x m m x x m x ⎧+≥⎪⎪⎪=++++-⎨⎪⎪--+≤-⎪⎩(2)<<当(,0)x ∈-∞时,()33(0)2223=343()2m x f x x x m x m x ⎧+-⎪⎪=+++⎨⎪--+≤-⎪⎩<<当302x -<<时,()=3+f x m ,当()3=432x f x x m ≤---+,单调递减,∴f (x )的最小值为3+m ,设()()20g x x x x=+<当20,x x x ->-+≥-2=x x --时,取等号2x x∴+≤即x g(x)取得最大值.要使()2f x x x≥+恒成立,只需3m +≥-m ≥-.。
2017—2018学年度第一学期期末联考试题高三数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分全卷满分150分,考试时间120分钟.注意:1. 考生在答题前,请务必将自己的姓名、准考证号等信息填在答题卡上.2. 选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,答在试卷上无效.3. 填空题和解答题用0.5毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内.答在试题卷上无效.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.把答案填在答题卡上对应题号后的框内,答在试卷上无效.1.设集合{123}A =,,,{45}B =,,{|}M x x a b a A b B ==+∈∈,,,则M 中的元素个数为A .3B .4C .5D .62.在北京召开的第24届国际数学家大会的会议,会议是根据中国古代数学家赵爽的弦图(如图)设计的,其由四个全等的直角三角形和一个正方形组成,若直角三角形的直角边的边长分别是3和4,在绘图内随机取一点,则此点取自直角三角形部分的概率为 A .125B .925C .1625D .24253.设i 为虚数单位,则下列命题成立的是A .a ∀∈R ,复数3i a --是纯虚数B .在复平面内i(2i)-对应的点位于第三限象C .若复数12i z =--,则存在复数1z ,使得1z z ∈RD .x ∈R ,方程2i 0x x +=无解4.等比数列{}n a 的前n 项和为n S ,已知3215109S a a a =+=,,则1a =A .19B .19-C .13D .13-5.已知曲线421y x ax =++在点(1(1))f --,处切线的斜率为8,则(1)f -=试卷类型:A天门 仙桃 潜江A .7B .-4C .-7D .4 6.84(1)(1)x y ++的展开式中22x y 的系数是A .56B .84C .112D .1687.已知一个空间几何体的三视图如图,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是 A .4cm 3B .5 cm 3C .6 cm 3D .7 cm 38.函数()sin()(0,0)f x A x A ωϕω=+>>的图像如图所示,则(1)(2)(3)(18)f f f f ++++的值等于ABC 2D .19.某算法的程序框图如图所示,其中输入的变量x 在1,2,3…,24 这24个整数中等可能随机产生。
2018届高三模拟 数学试题(理)一、选择题 (本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.已知集合1{,},(),3x M y y x x x R N y y x R ⎧⎫==-∈==∈⎨⎬⎩⎭,则( )A .M N =B .N M ⊆C .R M C N =D .R C N M 2. 复数(12)(2)z i i =++的共轭复数为( )A .-5iB .5iC .15i +D .15i - 3. 将函数()3sin(2)3f x x π=-的图像向右平移(0)m m >个单位后得到的图像关于原点对称,则m 的最小值是( )A .6π B .3π C .23π D .56π 4. 已知函数22()log f x x x =+,则不等式(1)(2)0f x f +-<的解集为( )A .(,1)(3,)-∞-+∞B .(,3)(1,)-∞-+∞C .(3,1)(1,1)---D .(1,1)(1,3)-5. 已知命题:,p a b R ∃∈, a b >且11a b >,命题:q x R ∀∈,3sin cos 2x x +<.下列命题是真命题的是( )A .p q ∧B .p q ⌝∧C .p q ∧⌝D .p q ⌝∧⌝ 6. 将正方体(如图1)截去三个三棱锥后,得到如图2所示的几何体,侧视图的视线方向如图2所示,则该几何体的侧视图为( )⊂≠7. 下列说法错误的是( )A .“函数()f x 的奇函数”是“(0)0f =”的充分不必要条件.B .已知A BC 、、不共线,若0PA PB PC ++=则P 是△ABC 的重心.C .命题“0x R ∃∈,0sin 1x ≥”的否定是:“x R ∀∈,sin 1x <”.D .命题“若3πα=,则1cos 2α=”的逆否命题是:“若1cos 2α≠,则3πα≠”. 8. 已知等比数列{}n a 的前n 项和为n S ,已知103010,130S S ==,则40S =( )A .-510B .400C . 400或-510D .30或40 9. 南宋数学家秦九韶在《数书九章》中提出的秦九韶,算法至今仍是多项式求值比较先进的算法.已知20172016()2018201721f x x x x =++++ ,下列程序框图设计的是求0()f x 的值,在“中应填的执行语句是( )A .n i =B .1n i =+C .n =2018i -D .n =2017i - 10. 已知34πθπ≤≤2=,则θ=( ) A . 101133ππ或 B .37471212ππ或 C .131544ππ或 D . 192366ππ或 11.已知△ABC中,,,a b c为角,,A B C的对边,0aBC bCA cAB ++=,则△ABC 的形状为( )A. 锐角三角形B. 直角三角形C. 钝角三角形D . 无法确定12. 我国古代太极图是一种优美的对称图.如果一个函数的图像能够将圆的面积和周长分成两个相等的部分,我们称这样的函数为圆的“太极函数”.下列命题中错误..命题的个数是( ) 1:P 对于任意一个圆其对应的太极函数不唯一;2:P 如果一个函数是两个圆的太极函数,那么这两个圆为同心圆;3:P 圆22(1)(1)4x y -+-=的一个太极函数为32()33f x x x x =-+; 4:P 圆的太极函数均是中心对称图形; 5:P 奇函数都是太极函数; 6:P 偶函数不可能是太极函数.A. 2B. 3C.4D.5二、填空题(本大题共4小题,每小题5分,共20分)13.已知平面向量(2,1),(2,).a b x == 且(2)()a b a b +⊥-,则x = .14.曲线2y x =与直线2y x =所围成的封闭图形的面积为 .15.已知等差数列{}n a 是递增数列,且1233a a a ++≤,7338a a -≤,则4a 的取值范围为 .16.()f x 是R 上可导的奇函数,()f x '是()f x 的导函数.已知0x >时()(),(1)f x f x f e '<=,不等式()ln(0ln(x f x e <≤的解集为M ,则在M 上()sin6g x x =的零点的个数为 .三、解答题(本大题共70分,解答应写出文字说明、证明过程或演算步骤。