山东省济宁市梁山一中高中数学《1.3.1柱体、锥体、台体的体积》学案新人教A版必修2

§1.3.1 柱体、椎体、台体的表面积与体积（第 1 课时）【教学目标】1.知识与技能目标（1）通过对柱、锥、台体的研究，掌握柱、锥、台的表面积的求法。

（2）能运用公式求解，柱体、锥体和台体的表面积，并且熟悉台体与柱体和锥体之间的转换关系。

（3）培养学生空间想象能力和思维能力。

2.过程与能力目标:（1）让学生经历几何体的侧面展开过程，感知几何体的形状。

（2）让学生通对照比较，理顺柱体、锥体、台体三间的表面积的关系。

3.情感与态度目标:通过学习，使学生感受到几何体面积的求解过程，对自己空间思维能力影响。

从而 增强学习的积极性。

【教学重难点】重点：柱体、锥体、台体的表面积计算.难点：理解计算公式的由来.【学情分析】根据学生的心理发展规律，采用学生参与的探究式讨论教学法。

在学生亲自动手去给出各种几何体的表面积的计算方法，特别注重不同解决问题的方法，提问不同层次的学生，面向全体，使基础差的学生也能有表现机会，培养其自信心，激发其学习兴趣。

有效的开发各层次学生的潜在智能，力求使学生能在原有的基础上得到发展。

启发学生从书本知识回到社会实践。

提供给学生与其生活和周围世界密切相关的数学知识，学习基础性的知识和技能，在教学中积极培养学生学习兴趣和动机，明确的学习目的，充分调动学生的学习积极性，激发学生对数学的兴趣!【教学过程】（一）创设情景，设置疑问，引入课题.（1）复习面积的概念以及所学基本平面图形的面积矩形的面积： S ab梯形的面积： S 1 (a b) h 2三 角 形 的 面 积 ： S 1 ah 1 ab sin C 22平行四边形的面积：S a ha b hb ab sin A圆形的面积： S r2扇形的面积： S 1 lr 1 r2 n r2 （n 为扇形的圆心角度数）22360（2）教师提出问题：在过去的学习中我们学习了正方体和长方体的表面积,以及 它们的展开图(多媒体展示),你知道上述几何体的展开图与其表面积的关系吗？引导学生回忆，互相交流，得出结论。

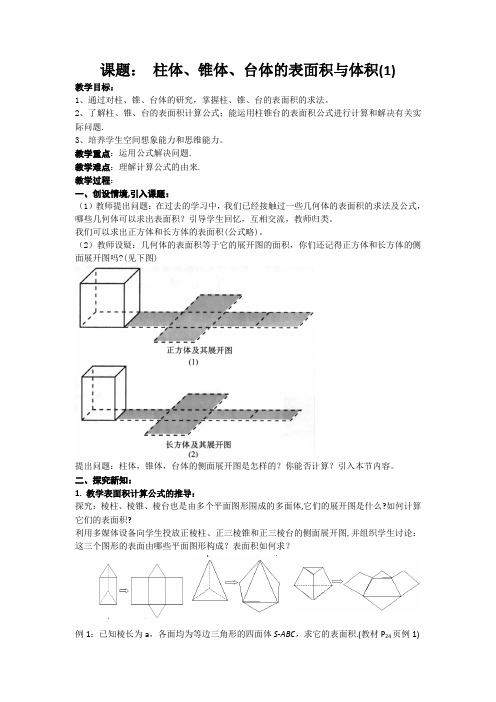
课题：柱体、锥体、台体的表面积与体积(1)教学目标：1、通过对柱、锥、台体的研究，掌握柱、锥、台的表面积的求法。

2、了解柱、锥、台的表面积计算公式；能运用柱锥台的表面积公式进行计算和解决有关实际问题.3、培养学生空间想象能力和思维能力。

教学重点：运用公式解决问题.教学难点：理解计算公式的由来.教学过程：一、创设情境,引入课题：（1）教师提出问题：在过去的学习中，我们已经接触过一些几何体的表面积的求法及公式，哪些几何体可以求出表面积？引导学生回忆，互相交流，教师归类。

我们可以求出正方体和长方体的表面积(公式略)。

（2）教师设疑：几何体的表面积等于它的展开图的面积，你们还记得正方体和长方体的侧面展开图吗?(见下图)提出问题：柱体，锥体，台体的侧面展开图是怎样的？你能否计算？引入本节内容。

二、探究新知：1. 教学表面积计算公式的推导：探究：棱柱、棱锥、棱台也是由多个平面图形围成的多面体,它们的展开图是什么?如何计算它们的表面积?利用多媒体设备向学生投放正棱柱、正三棱锥和正三棱台的侧面展开图,并组织学生讨论：这三个图形的表面由哪些平面图形构成？表面积如何求？例1：已知棱长为a，各面均为等边三角形的四面体S-ABC，求它的表面积.(教材P24页例1)SC AD练习：一个三棱柱的底面是正三角形，边长为4，侧棱与底面垂直，侧棱长10,求其表面积. 想一想：如何求圆柱、圆锥、圆台的侧面积及表面积？（图→侧→表）探究圆柱的表面积的求法：图柱的侧面展开图是矩形，长是圆柱底面圆周长，宽是圆柱的高（母线），设圆柱的底面半径为r,母线长为l ,则有:S 圆柱侧=2rl π，S 圆柱表=2()r r l π+，其中为r 圆柱底面半径，l 为母线长。

探究圆锥的表面积的求法：圆锥的侧面展开图为一个扇形，半径是圆锥的母线，弧长等于圆锥底面周长，侧面展开图扇形中心角为0360r lθ=⨯，S 圆锥侧=rl π，S 圆锥表=()r r l π+，其中为r 圆锥底面半径，l 为母线长。

【例3】牧民居住的蒙古包的形状是一个圆柱与圆锥的组合体，尺寸如右图所示，请你 帮助算出要搭建这样的一个蒙古包至少需要多少平方米的篷布？（精确到解：上部分圆锥体的母线长为 .1.2其侧面积为S 5 X72下部分圆柱体的侧面积为S （所以，搭建这样的一个蒙古包至少需要的篷布为 5-1.22 2.525 1.8 50.05 （n i ）.22 2.52 , 2.52 . 5 1.8.S S i S2 _______ 21.3.1柱体、锥体、台体的表面积一•学习目标：了解棱柱、棱锥、台的表面 积的计算公式（不要求记忆公式）；能运用 柱、锥、台的表面积进行计算和解决有关实际问题二.重点、难点： 重点： 难点：三.知识要点:表面积r 相关公式表面积相关公式棱柱S全% 2S底,其中S 侧1侧棱长gc 直截面周长圆柱S 全 2 r 22 rh（r :底面半径，h ： 高）棱锥S全 %S底圆锥S 全r 2rl （r :底面半径，1 :母 线长）棱台S全鼻S上底S下底圆台2 2S 全 （r' r r'l rl ）（r :下底半径，r :上底半径，| :母 线长）四•自主探究：（一）例题精讲：【例1】已知圆台的上下底面半径分别是 2、5,且侧面面积等于两底面面积之和，求该 圆台的母线长•解：设圆台的母线长为1,则 圆台的上底面面积为 S 上 22 4 , 圆台的上底面面积为 S T 2525 ,所以圆台的底面面积为 SS 上 S 下 29 又圆台的侧面积％（5)1 7 l ,于是7 125，即| 为所求.7【例2】一个正三棱柱的三视图如右图所示， 求这个正三棱柱的表面 积•解：由三视图知正三棱柱的高为2mm由左视图知正三棱柱的底面三角形的高为 2.3mm .设底面边长为a ,则一^ 2 3 , ••• a 42•正三棱柱的表面积为S S 侧 2S 底 3 4 2 2 ^ 4 2 3 24 8 3（mm 2）.点评：正确运用锥体和柱体的侧面积计算公式， 解决制作壳形几何体时的用料问题•注 意区分是面积计算，还是体积计算 •【例4】有一根长为10 cm 底面半径是0.5 cm 的圆柱形铁管，用一段铁丝在铁管上缠 绕8圈，并使铁丝的两个端点落在圆柱的同一母线的两端， 则铁丝的最短长度为多少厘米？ （精确到0.01 cm ）解：如图，把圆柱表面及缠绕其上的铁丝展开在平面上，得到矩形 ABCD 由题意知，BC =10 cm, AB 2 0.5 8 8 cm ，点A 与点C 就是铁丝的 起止位置，故线段 AC 的长度即为铁丝的最短长度 .- AC 102~（87 27.05 （cm ）.所以，铁丝的最短长度约为 27.05 cm .点评：此题关键是把圆柱 沿这条母线展开，将问题转 化为平面几何问题.探究几何体表面上最短距离，常将几何体的表面或侧面展开，化折（曲）为直，使空间图形问题转化为 平面图形问题.空间问题平面化，是解决立体几何问题基本的、常用的方法第.5练 § 1.3.1柱体、锥体、台体的表面积五•目标检测： （一）基础达标1 •用长为4，宽为2的矩形做侧面围成一个圆柱，此圆柱轴截面面积为（ ）.&六棱台的上、下底面均是正六边形，边长分别是 8 cm 和18 cm,侧面是全等的等腰 梯形，侧棱长为13 cm ,求它的表面积.A. 8B. 8C. 4D. 2 2. 圆台的一个底面周长是另一个底面周长的 则圆台较小底面的半径为（）.A. 7B. 6C. 53. —个圆柱的侧面展开图是一个正方形，A. 」B.」2 44•一个直棱柱（侧棱垂直于底面的棱柱）3倍，母线长为3,圆台的侧面积为84 ,和15cm,高是5cm,则这个直棱柱的侧面积是（2 2A. 160 cmB. 320 cmC.5. （04年湖北卷.文6）四面体ABCD 四个面的重心分别为 的表面积与四面体 A.丄 27ABC 啲表面积的比值是 1 1B • — C.-16 9 6.如图，已知圆柱体底面圆的半径为D. 3这个圆柱的全面积与侧面积的比是（ C.』 D.丄 2 的底面是菱形，棱柱的对角线长分别是）. 40 89 cn^ D. 80 89 cn iE F 、G H,则四面体 9cmEFGH（ ）.D.- 8 2-，高为2, AB , CD 分别是两底面的直径,AD , BC 是母线•若一只小虫从 A 点出发，从侧面爬行到 C 点，则小虫爬行的最短路 线的长度是 ____________ （结果保留根式）•7•已知两个母线长相等的圆锥的侧面展开图恰能拼成一个圆，且它们的侧面积之比为 1： 2，则它们的高之比为（二）能力提高9•一个圆锥的底面半径为R,高为H,在这个圆锥内部有一个高为x的内接圆柱.当x 为何值时，圆柱的表面积最大？最大值是多少？（三）探究创新10.现有一个长方体水箱，从水箱里面量得它的深是20cm.设水箱里盛有深为a cm的水，若往水箱里放入棱长为30cm 底面的长是25cm 宽是10cm的立方体铁块，试求水深.。

1.3.1 柱体、锥体、台体的表面积与体积目标定位 1.了解表面与展开图的关系.2.了解柱、锥、台体的表面积和体积计算公式；能运用柱、锥、台的表面积和体积公式进行计算和解决有关实际问题.自 主 预 习1.多面体的表面积多面体的表面积就是各个面的面积的和，也就是展开图的面积. 2.旋转体的表面积(1)柱体：柱体的底面面积为S ，高为h ，则V ＝Sh . (2)锥体：锥体的底面面积为S ，高为h ，则V ＝13Sh .(3)台体：台体的上、下底面面积分别为S ′、S ，高为h ，则V ＝13(S ′＋S ′S ＋S )h .即 时 自 测1.判断题(1)直棱柱的侧面展开图是矩形，一边是棱柱的侧棱，另一边等于棱柱的底面周长.(√) (2)圆锥的侧面展开图是一个等腰三角形.(×)(3)柱体的底面积为S ，高为h ，其体积V ＝Sh ，特别地，圆柱的底面半径为r ，高为h ；其体积V ＝πr 2h .(√)(4)已知圆锥SO 的底面半径r ＝2，高为4，则其体积为16π.(×) 提示 (2)圆锥的侧面展开图是一个扇形. (4)V ＝13π×22×4＝163π.2.圆锥的母线长为5，底面半径为3，则其侧面积等于( ) A.15B.15πC.24πD.30π解析 S 侧＝πrl ＝π×3×5＝15π. 答案 B3.将边长为1的正方形以其一边所在直线为旋转轴旋转一周，所得几何体的侧面积是( ) A.4πB.3πC.2πD.π解析 底面圆半径为1，高为1，侧面积S ＝2πrh ＝2π×1×1＝2π.故选C. 答案 C4.圆台OO ′的上、下底面半径分别为1和2，高为6，则其体积等于________. 解析 V ＝13π(12＋1×2＋22)×6＝14π.答案 14π类型一 空间几何体的表面积【例1】 如图所示，已知直角梯形ABCD ，BC ∥AD ，∠ABC ＝90°，AB ＝5 cm ，BC ＝16 cm ，AD ＝4 cm.求以AB 所在直线为轴旋转一周所得几何体的表面积.解 以AB 所在直线为轴旋转一周所得几何体是圆台，其上底半径是4 cm ，下底半径是16 cm ，母线DC ＝52＋（16－4）2＝13(cm).∴该几何体的表面积为π(4＋16)×13＋π×42＋π×162＝532π(cm 2).规律方法 1.圆柱、圆锥、圆台的相关几何量都集中体现在轴截面上，因此准确把握轴截面中的相关量是求解旋转体表面积的关键.2.棱锥及棱台的表面积计算常借助斜高、侧棱及其在底面的射影与高、底面边长等构成的直角三角形(或梯形)求解.【训练1】 如图，已知棱长为a ，各面均为等边三角形的四面体S －ABC ，求它的表面积.解 先求△SBC 的面积，过点S 作SD ⊥BC ，交BC 于点D . 因为BC ＝a ，SD ＝SB 2－BD 2＝a 2－⎝ ⎛⎭⎪⎫a 22＝32a . 所以S △SBC ＝12BC ·SD＝12a ×32a ＝34a 2. 因此，四面体S －ABC 的表面积S ＝4×34a 2＝3a 2. 类型二 空间几何体的体积(互动探究)【例2】 如图，三棱台ABC －A 1B 1C 1中，AB ∶A 1B 1＝1∶2，求三棱锥A 1－ABC ，三棱锥B －A 1B 1C ，三棱锥C －A 1B 1C 1的体积之比.[思路探究]探究点一 题中三棱台与三棱锥有什么关系？ 提示 题中三个三棱锥可看作是由三棱台分割而成的. 探究点二 求体积的常用方法有哪些？提示 求几何体体积的常用方法有：公式法，等积变换法，补体法，分割法. 解 设棱台的高为h ，S △ABC ＝S ，则S △A 1B 1C 1＝4S . ∴V A 1－ABC ＝13S △ABC ·h ＝13Sh ，V C －A 1B 1C 1＝13S △A 1B 1C 1·h ＝43Sh .又V 台＝13h (S ＋4S ＋2S )＝73Sh ，∴V B －A 1B 1C ＝V 台－V A 1－ABC －V C －A 1B 1C 1＝73Sh －Sh 3－4Sh 3＝23Sh ， ∴体积比为1∶2∶4.规律方法 求几何体体积的常用方法【训练2】 如图，在棱长为a 的正方体ABCD －A 1B 1C 1D 1中，求A 到平面A 1BD 的距离d .解 在三棱锥A 1－ABD 中，AA 1⊥平面ABD ，AB ＝AD ＝AA 1＝a ，A 1B ＝BD ＝A 1D ＝2a ，∵V A 1－ABD ＝V A －A 1BD ，∴13×12a 2·a ＝13×12×2a ×32·2a ·d . ∴d ＝33a .∴A 到平面A 1BD 的距离为33a . 类型三 与三视图有关的表面积、体积问题【例3】 一个四棱锥的侧棱长都相等，底面是正方形，其正视图如图所示，则该四棱锥侧面积和体积分别是( )A.45，8B.45，83C.4(5＋1)，83D.8，8解析 由正视图得出四棱锥的底面边长与高，进而求出侧面积与体积.由正视图知：四棱锥的底面是边长为2的正方形，四棱锥的高为2， ∴V ＝13×22×2＝83.四棱锥的侧面是全等的等腰三角形，底为2，高为5，∴S 侧＝4×12×2×5＝4 5.答案 B规律方法 1.解答此类问题的关键是先由三视图还原作出直观图，然后根据三视图中的数据在直观图中求出计算体积所需要的数据.2.若由三视图还原的几何体的直观图由几部分组成，求几何体的体积时，依据需要先将几何体分割分别求解，最后求和.【训练3】已知某三棱锥的三视图如图所示，则该三棱锥的体积是________．解析 由三视图可大致画出三棱锥的直观图如图，由正、俯视图可知，△ABC 为等腰三角形，且AC ＝23，AC 边上的高为1，∴S △ABC ＝12×23×1＝ 3.由侧视图可知：三棱锥的高h ＝1，∴V S －ABC ＝13S △ABC h ＝33.答案33[课堂小结]1.圆柱、圆锥、圆台的侧面积分别是它们侧面展开图的面积，因此弄清侧面展开图的形状及侧面展开图中各线段与原旋转体的关系，是掌握它们的侧面积公式及解有关问题的关键.2.计算柱体、锥体和台体的体积，关键是根据条件找出相应的底面面积和高，要充分运用多面体的有关截面及旋转体的轴截面，将空间问题转化为平面问题.3.在几何体的体积计算中，注意体会“分割思想”、“补体思想”及“等价转化思想”.1.已知长方体的过一个顶点的三条棱长的比是1∶2∶3，对角线的长是214，则这个长方体的体积是( ) A.6B.12C.24D.48解析 设长方体的过一个顶点的三条棱长分别为x 、2x 、3x ，又对角线长为214，则x 2＋(2x )2＋(3x )2＝(214)2，解得x ＝2.∴三条棱长分别为2、4、6. ∴V 长方体＝2×4×6＝48. 答案 D2.一个几何体的三视图及其尺寸如图(单位：cm)，则该几何体的表面积为( )A.12πB.18πC.24πD.36π解析 由三视图知该几何体为圆锥，底面半径r ＝3，母线l ＝5， ∴S 表＝πrl ＋πr 2＝24π.故选C. 答案 C3.一个圆柱的侧面展开图是一个正方形，则这个圆柱的表面积与侧面积的比为________. 解析 设底面半径为r ，侧面积为4π2r 2，表面积为2πr 2＋4π2r 2，其比为1＋2π2π.答案1＋2π2π4.在长方体ABCD －A 1B 1C 1D 1中，截下一个棱锥C －A 1DD 1求棱锥C －A 1DD 1的体积与剩余部分的体积之比.解 已知长方体可以看成直四棱柱，设它的底面ADD 1A 1的面积为S ，高为h ，则它的体积为V ＝Sh .而棱锥C －A 1DD 1的底面积为12S ，高为h ，故三棱锥C －A 1DD 1的体积：V C －A 1DD 1＝13×12Sh ＝16Sh ，余下部分体积为：Sh －16Sh ＝56Sh .所以棱锥C －A 1DD 1的体积与剩余部分的体积之比为1∶5.基 础 过 关1.圆台的上、下底面半径分别是3和4，母线长为6，则其表面积等于( ) A.72B.42πC.67πD.72π解析 S 圆台表＝S 圆台侧＋S 上底＋S 下底 ＝π(3＋4)·6＋π·32＋π·42＝67π. 答案 C2.如图所示，正方体ABCD －A 1B 1C 1D 1的棱长为1，则三棱锥D 1－ACD 的体积是( )A.16B.13C.12D.1解析 三棱锥D 1－ADC 的体积V ＝13S △ADC ×D 1D ＝13×12×AD ×DC ×D 1D ＝13×12×1×1×1＝16.答案 A3.一个四棱锥的侧棱长都相等，底面是正方形，其正(主)视图如下图所示该四棱锥侧面和体积分别是( )A.45，8B.45，83C.4(5＋1)，83D.8，8解析 由题意可知该四棱锥为正四棱锥，底面边长为2，高为2，侧面上的斜高为22＋12＝5，所以S 侧＝4×⎝ ⎛⎭⎪⎫12×2×5＝45，V ＝13×22×2＝83. 答案 B4.一个圆柱和一个圆锥的轴截面分别是边长为a 的正方形和正三角形，则它们的表面积之比为________.解析 S 圆柱＝2·π⎝ ⎛⎭⎪⎫a 22＋2π·⎝ ⎛⎭⎪⎫a 2·a ＝32πa 2，S 圆锥＝π⎝ ⎛⎭⎪⎫a 22＋π·a 2·a ＝34πa 2，∴S 圆柱∶S 圆锥＝2∶1.答案 2∶15.一个几何体的三视图如图所示(单位：m)，则该几何体的体积为________m 3.解析 根据三视图知，该几何体上部是一个底面直径为4 m ，高为2 m 的圆锥，下部是一个底面直径为2 m ，高为4 m 的圆柱.故该几何体的体积V ＝13π×22×2＋π×12×4＝20π3(m 3). 答案20π36.如图是某几何体的三视图.(1)画出它的直观图(不要求写画法)； (2)求这个几何体的表面积和体积. 解 (1)这个几何体的直观图如图所示.(2)这个几何体是一个简单组合体，它的下部是一个圆柱(底面半径为1，高为2)，它的上部是一个圆锥(底面半径为1，母线长为2，高为3)， 所以所求表面积为S ＝π×12＋2π×1×2＋π×1×2＝7π， 体积为V ＝π×12×2＋13×π×12×3＝2π＋33π.7.在△ABC 中，AC ＝3，BC ＝4，AB ＝5，以AB 所在直线为轴，三角形面旋转一周形成一旋转体，求此旋转体的表面积和体积.解 过C 点作CD ⊥AB ，垂足为D .以△ABC 中边AB 所在直线为轴旋转一周，所得到的旋转体是两个底面重合的圆锥，如图所示，这两个圆锥的高的和为AB ＝5，底面半径DC ＝AC ·BCAB＝125，故S 表＝π·DC ·(BC ＋AC )＝845π。

高中数学《&amp#167;1.3.1 柱体、锥体、台体的表面积与体积》学案新人教A版必修1、3、1 柱体、锥体、台体的表面积与体积（1）学习目标：1、理解和掌握柱、锥、台的表面积计算公式；2、能运用柱、锥、台的表面积公式进行计算和解决有关实际问题、学习重点：柱、锥、台表面积、体积的计算公式。

学习难点：利用相应公式求柱、锥、台表面积、体积。

课前预习（预习教材P23~ P25，找出疑惑之处）复习：斜二测画法画的直观图中，轴与轴的夹角为____，在原图中平行于轴或轴的线段画成与___和___保持平行；其中平行于轴的线段长度保持_____，平行于轴的线段长度____________、引入：研究空间几何体，除了研究结构特征和视图以外，还得研究它的表面积和体积、表面积是几何体表面的面积，表示几何体表面的大小；体积是几何体所占空间的大小、那么如何求柱、锥、台、球的表面积和体积呢？课内探究探究1：棱柱、棱锥、棱台的表面积问题：我们学习过正方体和长方体的表面积，以及它们的展开图（下图），你觉的它们展开图与其表面积有什么关系吗？结论：正方体、长方体是由多个平面围成的多面体，其表面积就是各个面的面积的和，也就是展开图的面积、新知1：棱柱、棱锥、棱台都是多面体，它们的表面积就是其侧面展开图的面积加上底面的面积、正四棱锥正四棱台正六棱柱试试1：想想下面多面体的侧面展开图都是什么样子，它们的表面积如何计算？探究2：圆柱、圆锥、圆台的表面积问题：根据圆柱、圆锥的几何特征，它们的侧面展开图是什么图形？它们的表面积等于什么？你能推导它们表面积的计算公式吗？新知2：（1）设圆柱的底面半径为，母线长为，则它的表面积等于圆柱的侧面积（矩形）加上底面积（两个圆），即、（2）设圆锥的底面半径为，母线长为，则它的表面积等于圆锥的侧面积（扇形）加上底面积（圆形），即、试试2：圆台的侧面展开图叫扇环，扇环是怎么得到的呢？（能否看作是个大扇形减去个小扇形呢）你能试着求出扇环的面积吗？从而圆台的表面积呢？新知3：设圆台的上、下底面半径分别为，，母线长为，则它的表面积等上、下底面的面积（大、小圆）加上侧面的面积（扇环），即、反思：想想圆柱、圆锥、圆台的结构，你觉得它们的侧面积之间有什么关系吗？例1 已知棱长为，各面均为等边三角形的四面体，求它的表面积、例2 如图,一个圆台形花盆盆口直径为20,盆底直径为15,底部渗水圆孔直径为,盆壁长15、为了美化花盆的外观,需要涂油漆、已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆(取3、14,结果精确到1毫升)? 动手试试练1、一个正三棱锥的侧面都是直角三角形，底面边长为，求它的表面积、练2、粉碎机的上料斗是正四棱台形状，它的上、下底面边长分别为80、440，高(上下底面的距离)是200, 计算制造这样一个下料斗所需铁板的面积、当堂检测1、正方体的表面积是64,则它对角线的长为（）、A、B、C、D、2、一个圆柱的侧面展开图是一个正方形,这个圆柱的表面积与侧面积的比是（）、A、B、C、D、3、一个正四棱台的两底面边长分别为,,侧面积等于两个底面积之和,则这个棱台的高为（）、A、B、C、D、4、如果圆锥的轴截面是正三角形,则该圆锥的侧面积与表面积的比是_____________、5、已知圆台的上、下底面半径和高的比为︰4︰4,母线长为10,则圆台的侧面积为___________、课后反思1、棱柱、棱锥、棱台及圆柱、圆锥、圆台的表面积计算公式；2、将空间图形问题转化为平面图形问题，是解决立体几何问题最基本、最常用的方法、知识拓展当柱体、锥体、台体是一些特殊的几何体,比如直棱柱、正棱锥、正棱台时，它们的展开图是一些规则的平面图形，表面积比较好求；当它们不是特殊的几何体，比如斜棱柱、不规则的四面体时，要注意分析各个面的形状、特点，看清楚题目所给的条件，想办法求出各个面的面积，最后相加、课后训练1、用长为4，宽为2的矩形做面围成一个圆柱，则此圆柱的侧面积为（）A、B、C、D、82、圆锥的底面半径为，母线长为，侧面展开图扇形的圆心角为，求证：（度）、3、如图，在长方体中，，，，且，求沿着长方体表面到的最短路线长、1、3、1 柱体、锥体、台体的表面积与体积（2）学习目标：1、了解柱、锥、台的体积计算公式；2、能运用柱、锥、台的体积公式进行计算和解决有关实际问题、学习重点：柱、锥、台表面积、体积的计算公式。

高一数学人教A 版必修2学案：1.3.1柱体 锥体 台体的体积学案
【学习目标】
【回顾·预习】
1、柱体、锥体、台体、球的结构特征
2、以前学习的柱体的体积
【自主·合作·探究】
1 正方体、长方体和圆柱的体积公式
V=
2.圆锥、棱锥的体积公式
V =
3、棱台、圆台的体积公式
V=
4、球的体积公式 已知球的半径为R ，则球的体积为
二、典型例题 【例4】如下图，在长方体1111ABCD A B C D -中，截下一个棱锥11C A DD -，求棱锥11CDD A -的体积与剩余部分的体积之比.
33 (7.8/)
() 5.8,,
12,10,10,( 3.14)?
g cm kg mm mm mm π例有一堆规格相同的铁制铁的密度是六角螺帽如下图共重已知底面是正六边形边长为内孔直径高为问这堆螺帽
大约有多少个
取
）球的表面积等于圆柱的侧面积
长方体的过一个顶点的三条棱长的比是
(C)24
B.
4，，以圆柱、圆锥、圆台的体积
3.一个几何体的三视图如图所示，其中正视图和侧视图均为边长是32的菱形，俯视图是一个正方形，
(A)1
3 (B)2
3 (C)1
6 (D)。

2021年高中数学1.3.1柱体、锥体、台体的表面积与体积新人教A版必修2【教学目标】1.通过对柱、锥、台体的研究，掌握柱、锥、台的表面积的求法。

2.通过对柱、锥、台体的研究，掌握柱、锥、台的体积的求法。

3.能运用公式求解，柱体、锥体和台全的全积，并且熟悉台体与术体和锥体之间的转换关系。

【教学重难点】教学重点：运用公式解决问题教学难点：理解计算公式的由来.【教学过程】（一）情景导入讨论：正方体、长方体的侧面展开图？→正方体、长方体的表面积计算公式？讨论：圆柱、圆锥的侧面展开图？→圆柱的侧面积公式？圆锥的侧面积公式？那么如何计算柱体、锥体、台体的表面积,进而去研究他们的体积问题,这是我们这节主要学习的内容。

（二）展示目标这也是我们今天要学习的主要内容:1.通过对柱、锥、台体的研究，掌握柱、锥、台的表面积的求法。

2.通过对柱、锥、台体的研究，掌握柱、锥、台的体积的求法。

3.能运用公式求解，柱体、锥体和台全的全积，并且熟悉台体与术体和锥体之间的转换关系。

（三）检查预习1．棱柱的侧面展开图是由，棱锥的侧面展开图是由，梭台的侧面展开图是由，圆柱的侧面展开图是，圆锥的侧面展开图是，圆台的侧面展开图是。

2．几何体的表面积是指，棱柱、棱锥、棱台的表面积问题就是求、，圆柱、圆锥、圆台的表面积问题就是求、、、。

3．几何体的体积是指，一个几何体的体积等于。

（四）合作探究面积探究:讨论：如何求棱柱、棱锥、棱台等多面体的表面积？（展开成平面图形，各面面积和） 讨论：如何求圆柱、圆锥、圆台的侧面积及表面积？（图→侧→表） 体积探究:讨论：正方体、长方体、圆柱、圆锥的体积计算公式？ 五）交流展示 略（六）精讲精练1. 教学表面积计算公式的推导：① 讨论：如何求棱柱、棱锥、棱台等多面体的表面积？（展开成平面图形，各面面积和）② 练习：1.已知棱长为a ，各面均为等边三角形的正四面体S-ABC 的表面积.(教材P 24页例1)2. 一个三棱柱的底面是正三角形，边长为4，侧棱与底面垂直，侧棱长10,求其表面积.③ 讨论：如何求圆柱、圆锥、圆台的侧面积及表面积？（图→侧→表）圆柱：侧面展开图是矩形，长是圆柱底面圆周长，宽是圆柱的高（母线）， S=2，S=2，其中为圆柱底面半径，为母线长。

1. 3.1柱体、锥体、台体的表面积与体积【教学目标】1.通过对柱、锥、台体的研究，掌握柱、锥、台的表面积的求法。

2.通过对柱、锥、台体的研究，掌握柱、锥、台的体积的求法。

3.能运用公式求解，柱体、锥体和台全的全积，并且熟悉台体与术体和锥体之间的转换关系。

【教学重难点】教学重点：运用公式解决问题教学难点：理解计算公式的由来.【教学过程】（一）情景导入讨论：正方体、长方体的侧面展开图？→正方体、长方体的表面积计算公式？讨论：圆柱、圆锥的侧面展开图？→圆柱的侧面积公式？圆锥的侧面积公式？那么如何计算柱体、锥体、台体的表面积,进而去研究他们的体积问题,这是我们这节主要学习的内容。

（二）展示目标这也是我们今天要学习的主要内容:1.通过对柱、锥、台体的研究，掌握柱、锥、台的表面积的求法。

2.通过对柱、锥、台体的研究，掌握柱、锥、台的体积的求法。

3.能运用公式求解，柱体、锥体和台全的全积，并且熟悉台体与术体和锥体之间的转换关系。

（三）检查预习1．棱柱的侧面展开图是由，棱锥的侧面展开图是由，梭台的侧面展开图是由，圆柱的侧面展开图是，圆锥的侧面展开图是，圆台的侧面展开图是。

2．几何体的表面积是指，棱柱、棱锥、棱台的表面积问题就是求、，圆柱、圆锥、圆台的表面积问题就是求、、、。

3．几何体的体积是指，一个几何体的体积等于。

（四）合作探究面积探究:讨论：如何求棱柱、棱锥、棱台等多面体的表面积？（展开成平面图形，各面面积和）讨论：如何求圆柱、圆锥、圆台的侧面积及表面积？（图→侧→表）体积探究:讨论：正方体、长方体、圆柱、圆锥的体积计算公式？五）交流展示略（六）精讲精练1. 教学表面积计算公式的推导：①讨论：如何求棱柱、棱锥、棱台等多面体的表面积？（展开成平面图形，各面面积和）②练习：1.已知棱长为a，各面均为等边三角形的正四面体S-ABC的表面积.(教材P24页例1)2. 一个三棱柱的底面是正三角形，边长为4，侧棱与底面垂直，侧棱长10,求其表面积.③讨论：如何求圆柱、圆锥、圆台的侧面积及表面积？（图→侧→表）圆柱：侧面展开图是矩形，长是圆柱底面圆周长，宽是圆柱的高（母线）， S=2，S=2，其中为圆柱底面半径，为母线长。

1.3 空间几何体的表面积与体积1.3.1 柱体、锥体、台体的表面积与体积整体设计教学分析本节一开始的“思考”从学生熟悉的正方体和长方体的展开图入手，分析展开图与其表面积的关系，目的有两个：其一，复习表面积的概念，即表面积是各个面的面积的和；其二，介绍求几何体表面积的方法，把它们展成平面图形，利用平面图形求面积的方法，求立体图形的表面积.接着，教科书安排了一个“探究”，要求学生类比正方体、长方体的表面积，讨论棱柱、棱锥、棱台的表面积问题，并通过例1进一步加深学生的认识.教学中可以引导学生讨论得出：棱柱的展开图是由平行四边形组成的平面图形，棱锥的展开图是由三角形组成的平面图形，棱台的展形图是由梯形组成的平面图形.这样，求它们的表面积的问题就可转化为求平行四边形、三角形和梯形的面积问题.教科书通过“思考”提出“如何根据圆柱、圆锥的几何结构特征，求它们的表面积？”的问题.教学中可引导学生回忆圆柱、圆锥的形成过程及其几何特征，在此基础上得出圆柱的侧面可以展开成为一个矩形，圆锥的侧面可以展开成为一个扇形的结论，随后的有关圆台表面积问题的“探究”，也可以按照这样的思路进行教学.值得注意的是，圆柱、圆锥、圆台都有统一的表面积公式，得出这些公式的关键是要分析清楚它们的底面半径、母线长与对应的侧面展开图中的边长之间的关系，教学中应当引导学生认真分析，在分别学习了圆柱、圆锥、圆台的表面积公式后，可以引导学生用运动、变化的观点分析它们之间的关系.由于圆柱可看成上下两底面全等的圆台；圆锥可看成上底面半径为零的圆台，因此圆柱、圆锥就可以看成圆台的特例.这样，圆柱、圆锥的表面积公式就可以统一在圆台的表面积公式之下.关于体积的教学.我们知道，几何体占有空间部分的大小，叫做几何体的体积.这里的“大小”没有比较大小的含义，而是要用具体的“数”来定量的表示几何体占据了多大的空间，因此就产生了度量体积的问题.度量体积时应知道：①完全相同的几何体，它的体积相等；一个几何体的体积等于它的各部分体积的和.体积相等的两个几何体叫做等积体.相同的两个几何体一定是等积体，但两个等积体不一定相同.体积公式的推导是建立在等体积概念之上的.柱体和锥体的体积计算，是经常要解决的问题.虽然有关公式学生已有所了解，但进一步了解这些公式的推导，有助于学生理解和掌握这些公式，为此，教科书安排了一个“探究”，要求学生思考一下棱锥与等底等高的棱柱体积之间的关系.教学中，可以引导学生类比圆柱与圆锥之间的体积关系来得出结论.与讨论表面积公式之间的关系类似，教科书在得出柱体、锥体、台体的体积公式后，安排了一个“思考”，目的是引导学生思考这些公式之间的关系，建立它们之间的联系.实际上，这几个公式之间的关系，是由柱体、锥体和台体之间的关系决定的.这样，在台体的体积公式中，令S′=S，得柱体的体积公式；令S′=0，得锥体的体积公式.值得注意的是在教学过程中，要重视发挥思考和探究等栏目的作用，培养学生的类比思维能力，引导学生发现这些公式之间的关系，建立它们的联系.本节的重点应放在公式的应用上，防止出现：教师在公式推导过程中“纠缠不止”，要留出“空白”，让学生自己去思考和解决问题.如果有条件，可以借助于信息技术来展示几何体的展开图.对于空间想象能力较差的学生，可以通过制作实物模型，经过操作确认来增强空间想象能力.三维目标1.了解柱体、锥体、台体的表面积和体积计算公式（不要求记忆），提高学生的空间想象能力和几何直观能力，培养学生的应用意识，增加学生学习数学的兴趣.2.掌握简单几何体的体积与表面积的求法，提高学生的运算能力，培养学生转化、化归以及类比的能力. 重点难点教学重点：了解柱体、锥体、台体的表面积和体积计算公式及其应用.教学难点：表面积和体积计算公式的应用.课时安排1课时教学过程导入新课思路1.在过去的学习中，我们已经接触过一些几何体的面积和体积的求法及公式，哪些几何体可以求出表面积和体积？（引导学生回忆，互相交流，教师归类）几何体的表面积等于它的展开图的面积，那么，柱体、锥体、台体的侧面展开图是怎样的？你能否计算？思路2.被誉为世界七大奇迹之首的胡夫大金字塔，在1889年巴黎埃菲尔铁塔落成前的四千多年的漫长岁月中，胡夫大金字塔一直是世界上最高的建筑物.在四千多年前生产工具很落后的中古时代，埃及人是怎样采集、搬运数量如此之多，每块又如此之重的巨石垒成如此宏伟的大金字塔，真是一个十分难解的谜.胡夫大金字塔是一个正四棱锥外形的建筑，塔底边长230米，塔高146.5米，你能计算建此金字塔用了多少石块吗？推进新课新知探究提出问题①在初中，我们已经学习了正方体和长方体的表面积，以及它们的展开图（图1），你知道上述几何体的展开图与其表面积的关系吗？正方体及其展开图(1) 长方体及其展开图(2)图1②棱柱、棱锥、棱台也是由多个平面图形围成的几何体，它们的展开图是什么？如何计算它们的表面积？③如何根据圆柱、圆锥的几何结构特征，求它们的表面积？④联系圆柱、圆锥的侧面展开图，你能想象圆台侧面展开图的形状，并且画出它吗？如果圆台的上、下底面半径分别是r′,r，母线长为l，你能计算出它的表面积吗？⑤圆柱、圆锥和圆台的表面积之间有什么关系？活动：①学生讨论和回顾长方体和正方体的表面积公式.②学生思考几何体的表面积的含义，教师提示就是求各个面的面积的和.③让学生思考圆柱和圆锥的侧面展开图的形状.④学生思考圆台的侧面展开图的形状.⑤提示学生用动态的观点看待这个问题.讨论结果：①正方体、长方体是由多个平面图形围成的几何体，它们的表面积就是各个面的面积的和.因此，我们可以把它们展成平面图形，利用平面图形求面积的方法，求立体图形的表面积.②棱柱的侧面展开图是平行四边形，其表面积等于围成棱柱的各个面的面积的和；棱锥的侧面展开图是由多个三角形拼接成的，其表面积等于围成棱锥的各个面的面积的和；棱台的侧面展开图是由多个梯形拼接成的，其表面积等于围成棱台的各个面的面积的和.③它们的表面积等于侧面积与底面积的和，利用它们的侧面展开图来求得它们的侧面积，由于底面是圆面，其底面积直接应用圆的面积公式即得.其中，圆柱的侧面展开图是矩形，圆锥的侧面展开图是扇形.我们知道，圆柱的侧面展开图是一个矩形（图2）.如果圆柱的底面半径为r,母线长为l，那么圆柱的底面面积为πr2,侧面面积为2πrl.因此，圆柱的表面积S=2πr2+2πrl=2πr(r+l).图2 图3圆锥的侧面展开图是一个扇形（图3）.如果圆锥的底面半径为r,母线长为l，那么它的表面积S=πr2+πrl=πr(r+l).点评：将空间图形问题转化为平面图形问题，是解决立体几何问题基本的、常用的方法.④圆台的侧面展开图是一个扇环（图4），它的表面积等于上、下两个底面的面积和加上侧面的面积，即S=π(r2+r′2+rl+r′l).图4⑤圆柱、圆锥、圆台侧面积的关系：圆柱和圆锥都可以看作是圆台退化而成的几何体.圆柱可以看作是上下底面全等的圆台，圆锥可看作是上底面退化成一点的圆台，观察它们的侧面积，不难发现：S 圆柱表=2πr(r+l)−−−←==r r r 21S 圆台表=π(r 1l+r 2l+r 12+r 22)−−−→−==rr r 21,0S 圆锥表=πr(r+l).从上面可以很清楚地看出圆柱和圆锥的侧面积公式都可以看作由圆台侧面积公式演变而来.提出问题①回顾长方体、正方体和圆柱的体积公式，你能将它们统一成一种形式吗？并依次类比出柱体的体积公式？②比较柱体、锥体、台体的体积公式：V 柱体=Sh(S 为底面积，h 为柱体的高)； V 锥体=Sh 31(S 为底面积，h 为锥体的高)； V 台体=)''(31S SS S ++h(S′,S 分别为上、下底面积，h 为台体的高). 你能发现三者之间的关系吗？柱体、锥体是否可以看作“特殊”的台体？其体积公式是否可以看作台体体积公式的“特殊”形式？活动：①让学生思考和讨论交流长方体、正方体和圆柱的体积公式.②让学生类比圆柱、圆锥和圆台的表面积的关系？讨论结果：①棱长为a 的正方体的体积V=a 3=a 2a=Sh ；长方体的长、宽和高分别为a,b,c ，其体积为V=abc=(ab)c=Sh ；底面半径为r 高为h 的圆柱的体积是V=πr 2h=Sh ，可以类比，一般的柱体的体积也是V=Sh ，其中S 是底面面积，h 为柱体的高.圆锥的体积公式是V=Sh 31(S 为底面面积，h 为高)，它是同底等高的圆柱的体积的31. 棱锥的体积也是同底等高的棱柱体积的31,即棱锥的体积V=Sh 31 (S 为底面面积，h 为高). 由此可见，棱柱与圆柱的体积公式类似，都是底面面积乘高；棱锥与圆锥的体积公式类似，都是底面面积乘高的31. 由于圆台（棱台）是由圆锥（棱锥）截成的，因此可以利用两个锥体的体积差，得到圆台（棱台）的体积公式V=31(S′+S S '+S)h, 其中S′，S 分别为上、下底面面积，h 为圆台（棱台）高.注意：不要求推导公式，也不要求记忆.②柱体可以看作是上、下底面相同的台体，锥体可以看作是有一个底面是一个点的台体.因此柱体、锥体可以看作“特殊”的台体.当S′=0时，台体的体积公式变为锥体的体积公式;当S′=S 时，台体的体积公式变为柱体的体积公式，因此，柱体、锥体的体积公式可以看作台体体积公式的“特殊”形式.柱体和锥体可以看作由台体变化得到，柱体可以看作是上、下底面相同的台体，锥体可以看作是有一个底面是一个点的台体，因此很容易得出它们之间的体积关系,如图5：图5应用示例思路1例1 已知棱长为a ，各面均为等边三角形的四面体S —ABC （图6），求它的表面积.图6活动：回顾几何体的表面积含义和求法.分析：由于四面体S —ABC 的四个面是全等的等边三角形，所以四面体的表面积等于其中任何一个面面积的4倍.解：先求△SBC 的面积，过点S 作SD⊥BC，交BC 于点D.因为BC=a,SD=a a a BDSB 23)2(2222=-=-, 所以S △SBC =21BC·SD=2432321a a a =⨯. 因此，四面体S —ABC 的表面积S=4×22343a a =. 点评：本题主要考查多面体的表面积的求法.变式训练1.已知圆柱和圆锥的高、底面半径均分别相等.若圆柱的底面半径为r ，圆柱侧面积为S ，求圆锥的侧面积. 解：设圆锥的母线长为l ，因为圆柱的侧面积为S ，圆柱的底面半径为r ，即S 圆柱侧=S ，根据圆柱的侧面积公式可得：圆柱的母线（高）长为r S π2，由题意得圆锥的高为r S π2，又圆锥的底面半径为r ，根据勾股定理，圆锥的母线长l=22)2(r S r π+，根据圆锥的侧面积公式得 S 圆锥侧=πrl=π·r·24)2(24222S r r S r +=+ππ. 2.两个平行于圆锥底面的平面将圆锥的高分成相等的三段，那么圆锥被分成的三部分的体积的比是（ ）A.1∶2∶3B.1∶7∶19C.3∶4∶5D.1∶9∶27分析：因为圆锥的高被分成的三部分相等，所以两个截面的半径与原圆锥底面半径之比为1∶2∶3，于是自上而下三个圆锥的体积之比为(h r 23π)∶［2)2(3r π·2h］∶［2)3(3r π·3h］=1∶8∶27，所以圆锥被分成的三部分的体积之比为1∶（8－1）∶（27－8）=1∶7∶19.答案：B3.三棱锥V —ABC 的中截面是△A 1B 1C 1，则三棱锥V —A 1B 1C 1与三棱锥A —A 1BC 的体积之比是（ ）A.1∶2B.1∶4C.1∶6D.1∶8分析：中截面将三棱锥的高分成相等的两部分，所以截面与原底面的面积之比为1∶4，将三棱锥A —A 1BC 转化为三棱锥A 1—ABC ，这样三棱锥V —A 1B 1C 1与三棱锥A 1—ABC 的高相等，底面积之比为1∶4，于是其体积之比为1∶4.答案：B例2 如图7，一个圆台形花盆盆口直径为20 cm ，盆底直径为，底部渗水圆孔直径为1.5 cm ，盆壁长为15 cm.为了美化花盆的外观，需要涂油漆.已知每平方米用100毫升油漆，涂100个这样的花盆需要多少毫升油漆？（π取3.14，结果精确到1毫升，可用计算器）图7活动：学生思考和讨论如何转化为数学问题.只要求出每个花盆外壁的表面积，就可以求出油漆的用量.而花盆外壁的表面积等于花盆的侧面积加上底面积，再减去底面圆孔的面积.解：如图7，由圆台的表面积公式得一个花盆外壁的表面积S=π［1522015215)215(2⨯+⨯+］-π(25.1)2≈1 000(cm 2)=0.1(m 2).涂100个这样的花盆需油漆：0.1×100×100=1 000（毫升）.答：涂100个这样的花盆需要1 000毫升油漆.点评：本题主要考查几何体的表面积公式及其应用.变式训练1.有位油漆工用一把长度为50 cm ，横截面半径为10 cm 的圆柱形刷子给一块面积为10 m 2的木板涂油漆，且圆柱形刷子以每秒5周的速度在木板上匀速滚动前进，则油漆工完成任务所需的时间是多少?（精确到0.01秒）解：圆柱形刷子滚动一周涂过的面积就等于圆柱的侧面积，∵圆柱的侧面积为S 侧=2πrl=2π·0.1·0.5=0.1π m 2，又∵圆柱形刷子以每秒5周匀速滚动，∴圆柱形刷子每秒滚过的面积为0.5π m 2，因此油漆工完成任务所需的时间t=ππ205.01022=mm ≈6.37秒. 点评：本题虽然是实际问题，但是通过仔细分析后，还是归为圆柱的侧面积问题.解决此题的关键是注意到圆柱形刷子滚动一周所经过的面积就相当于把圆柱的侧面展开的面积，即滚动一周所经过的面积等于圆柱的侧面积.从而使问题迎刃而解.2.（2007山东滨州一模，文14）已知三棱锥O —ABC 中，OA 、OB 、OC 两两垂直，OC=1,OA=x ，OB=y ，且x+y=4，则三棱锥体积的最大值是___________.分析：由题意得三棱锥的体积是61)4(612131-=-=⨯x x xy (x-2)2+32，由于x ＞0，则当x=2时，三棱锥的体积取最大值32. 答案：32 例3 有一堆规格相同的铁制（铁的密度是7.8 g/cm 3）六角螺帽（图8）共重5.8 kg,已知底面是正六边形，边长为12 mm,内孔直径为10 mm,高为10 mm ，问这堆螺帽大约有多少个?（π取3.14）图8活动：让学生讨论和交流如何转化为数学问题.六角帽表示的几何体是一个组合体，在一个六棱柱中间挖去一个圆柱，因此它的体积等于六棱柱的体积减去圆柱的体积.解：六角螺帽的体积是六棱柱体积与圆柱体积的差，即V=43×122×6×10-3.14×(210)2×10≈2 956(mm 3)=2.956(cm 3).所以螺帽的个数为5.8×1 000÷(7.8×2.956)≈252(个).答：这堆螺帽大约有252个.点评：本题主要考查几何体的体积公式及其应用.变式训练如图9，有个水平放置圆台形容器，上、下底面半径分别为2分米，4分米，高为5分米，现以每秒3立方分米的速度往容器里面注水，当水面的高度为3分米时，求所用的时间.（精确到0.01秒）图9解：如图10，设水面的半径为r ，则EH=r-2分米，BG=2分米，图10在△ABG 中，∵EH∥BG， ∴BGEH AG AH =.∵AH=2分米, ∴2252-=r .∴r=514分米. ∴当水面的高度为3分米时，容器中水的体积为V 水=π31·3［(514)2+514×4+42］=25876π立方分米, ∴所用的时间为25292325876ππ=≈36.69秒. 答：所用的时间为36.69秒.思路2例1 （2007山东烟台高三期末统考，理8）如图11所示，一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为1，那么这个几何体的体积为（ ）图11 A.1 B.21 C.31 D.61 活动：让学生将三视图还原为实物图，讨论和交流该几何体的结构特征.分析：根据三视图，可知该几何体是三棱锥，图12所示为该三棱锥的直观图，并且侧棱PA⊥AB，PA⊥AC ，AB⊥AC.则该三棱锥的高是PA ，底面三角形是直角三角形，所以这个几何体的体积为V=611213131=⨯⨯=∆PA S ABC .图12答案：D点评：本题主要考查几何体的三视图和体积.给出几何体的三视图，求该几何体的体积或面积时，首先根据三视图确定该几何体的结构特征，再利用公式求得.此类题目成为新课标高考的热点，应引起重视. 变式训练1.（2007山东泰安高三期末统考，理8）若一个正三棱柱的三视图如图13所示，则这个正三棱柱的表面积为（ ）图13 A.318 B.315 C.3824+ D.31624+分析：该正三棱柱的直观图如图14所示，且底面等边三角形的高为32，正三棱柱的高为2，则底面等边三角形的边长为4，所以该正三棱柱的表面积为 3×4×2+2×21×4×32=24+38.图14答案：C2.（2007山东潍坊高三期末统考，文3）如果一个空间几何体的正视图与侧视图均为全等的等边三角形，俯视图为一个半径为1的圆及其圆心，那么这个几何体的体积为（ ） A.33π B.332π C.π3 D.3π 分析：由三视图知该几何体是圆锥，且轴截面是等边三角形，其边长等于底面直径2，则圆锥的高是轴截面等边三角形的高为3，所以这个几何体的体积为V=3331312ππ=⨯⨯⨯. 答案：A3.（2007广东高考，文17）已知某几何体的俯视图是如图15所示的矩形，正视图（或称主视图）是一个底边长为8、高为4的等腰三角形，侧视图（或称左视图）是一个底边长为6、高为4的等腰三角形.图15（1）求该几何体的体积V ；（2）求该几何体的侧面积S.解：由三视图可知该几何体是一个底面边长分别为6、8的矩形，高为4的四棱锥.设底面矩形为ABCD.如图16所示，AB=8，BC=6，高VO=4.图16（1）V=31×(8×6)×4=64. (2)设四棱锥侧面VAD 、VBC 是全等的等腰三角形，侧面VAB 、VCD 也是全等的等腰三角形，在△VBC 中，BC 边上的高为h 1=24)28(4)2(2222=+=+AB VO , 在△VAB 中，AB 边上的高为h 2=2222)26(4)2(+=+BC VO =5. 所以此几何体的侧面积S=)582124621(2⨯⨯+⨯⨯=40+224. 点评：高考试题中对面积和体积的考查有三种方式，一是给出三视图，求其面积或体积；二是与的组合体有关的面积和体积的计算；三是在解答题中，作为最后一问.例2 图17所示的几何体是一棱长为4 cm 的正方体，若在它的各个面的中心位置上，各打一个直径为2 cm 、深为1 cm 的圆柱形的孔，求打孔后几何体的表面积是多少?（π取3.14）图17活动：因为正方体的棱长为4 cm ，而孔深只有1 cm ，所以正方体没有被打透.这样一来打孔后所得几何体的表面积，等于原来正方体的表面积，再加上六个完全一样的圆柱的侧面积，这六个圆柱的高为1 cm ，底面圆的半径为1 cm.解：正方体的表面积为16×6=96（cm 2），一个圆柱的侧面积为2π×1×1=6.28（cm 2），则打孔后几何体的表面积为96＋6.28×6=133.68（cm 2）.答：几何体的表面积为133.68 cm 2.点评：本题主要考查正方体、圆柱的表面积.求几何体的表面积问题，通常将所给几何体分成基本的柱、锥、台，再通过这些基本柱、锥、台的表面积，进行求和或作差，从而获得几何体的表面积.本题中将几何体的表面积表达为正方体的表面积与六个圆柱侧面积的和是非常有创意的想法，如果忽略正方体没有被打透这一点，思考就会变得复杂，当然结果也会是错误的.变式训练图18所示是由18个边长为1 cm 的小正方体拼成的几何体，求此几何体的表面积.图18分析：从图18中可以看出，18个小正方体一共摆了三层，第一层2个，第二层7个，因为18-7-2=9，所以第三层摆了9个.另外，上、下两个面的表面积是相同的，同样，前、后,左、右两个面的表面积也是分别相同的.解：因为小正方体的棱长是1 cm ，所以上面的表面积为12×9=9（ cm 2），前面的表面积为12×8=8（ cm 2），左面的表面积为12×7=7（ cm 2），则此几何体的表面积为9×2+8×2+7×2=48( cm 2).答：此几何体的表面积为48 cm 2.知能训练1.正方体的表面积是96，则正方体的体积是（ ） A.648 B.64 C.16 D.96分析：设正方体的棱长为a ，则6a 2=96，解得a=4，则正方体的体积是a 3=64.答案：B2.（2007山东临沂高三期末统考，文2）如图19所示，圆锥的底面半径为1，高为3，则圆锥的表面积为（ ）A.πB.2πC.3πD.4π分析：设圆锥的母线长为l ，则l=13+=2，所以圆锥的表面积为S=π×1×(1+2)=3π.答案：C3.正三棱锥的底面边长为3，侧棱长为32，则这个正三棱锥的体积是（ ） A.427 B.49 C.4327 D.439 分析：可得正三棱锥的高h=22)3()32(-=3，于是V=4393343312=⨯⨯⨯. 答案：D4.若圆柱的高扩大为原来的4倍，底面半径不变，则圆柱的体积扩大为原来的_________倍；若圆柱的高不变，底面半径扩大为原来的4倍，则圆柱的体积扩大为原来的_________倍.分析：圆柱的体积公式为V 圆柱=πr 2h ，底面半径不变，高扩大为原来的4倍，其体积也变为原来的4倍；当圆柱的高不变，底面半径扩大为原来的4倍时，其体积变为原来的42=16倍.答案：4 165.图20是一个正方体，H 、G 、F 分别是棱AB 、AD 、AA 1的中点.现在沿△GFH 所在平面锯掉正方体的一个角，问锯掉部分的体积是原正方体体积的几分之几?图20分析：因为锯掉的是正方体的一个角，所以HA 与AG 、AF 都垂直，即HA 垂直于立方体的上底面，实际上锯掉的这个角，是以三角形AGF 为底面，H 为顶点的一个三棱锥.解：设正方体的棱长为a ，则正方体的体积为a 3.三棱锥的底面是Rt△AGF，即∠FAG 为90°，G 、F 又分别为AD 、AA 1的中点，所以AF=AG=a 21.所以△AGF 的面积为281212121a a a =⨯⨯.又因AH 是三棱锥的高，H 又是AB 的中点，所以AH=a 21.所以锯掉的部分的体积为32481812131a a a =⨯⨯. 又因48148133=÷a a ,所以锯掉的那块的体积是原正方体体积的481. 6.（2007山东临沂高三期末考试，理13）已知一圆锥的侧面展开图为半圆，且面积为S ，则圆锥的底面面积是____________.分析：如图21，设圆锥底面半径为r ，母线长为l ，由题意得⎪⎩⎪⎨⎧==,2,22r l S l πππ解得r=π2S ，所以圆锥的底面积为πr 2=22S S =⨯ππ.图21 答案：2S 7.如图22，一个正三棱柱容器，底面边长为a ，高为2a ，内装水若干，将容器放倒，把一个侧面作为底面，如图23，这时水面恰好为中截面，则图22中容器内水面的高度是_________.图22 图23分析：图22中容器内水面的高度为h ，水的体积为V ，则V=S △ABC h.又图23中水组成了一个直四棱柱，其底面积为ABC S ∆43，高度为2a ，则V=ABC S ∆43·2a，∴h=a S a S ABC ABC 23243=∙∆∆. 答案：a 23 8.圆台的两个底面半径分别为2、4，截得这个圆台的圆锥的高为6，则这个圆台的体积是_____________. 分析：设这个圆台的高为h ，画出圆台的轴截面，可得6642h -=，解得h=3，所以这个圆台的体积是3π(22+2×4+42)×3=28π. 答案：28π9.已知某个几何体的三视图如图24，根据图中标出的尺寸（单位：cm ）,可得这个几何体的体积是（ ）图24 A.34000 cm 3 B.38000cm 3 C.2 000 cm 3 D.4 000 cm 3 分析：该几何体是四棱锥，并且长为20 cm 的一条侧棱垂直于底面，所以四棱锥的高为20 cm,底面是边长为20 cm 的正方形（如俯视图），所以底面积是20×20=400 cm 2，所以该几何体的体积是31×400×20=38000cm 3. 答案：B11 拓展提升 问题：有两个相同的直三棱柱，高为a2，底面三角形的三边长分别为3a,4a,5a(a ＞0).用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，表面积最小的是一个四棱柱，则a 的取值范围是___________. 探究：两个相同的直三棱柱并排放拼成一个三棱柱或四棱柱，有三种情况：四棱柱有一种，就是边长为5a 的边重合在一起，表面积为24a 2+28，三棱柱有两种，边长为4a 的边重合在一起，表面积为24a 2+32，边长为3a 的边重合在一起，表面积为24a 2+36，两个相同的直三棱柱竖直放在一起，有一种情况，表面积为12a 2+48,最小的是一个四棱柱，这说明24a 2+28＜12a 2+48⇒12a 2＜20⇒0＜a ＜315. 答案：0＜a ＜315 课堂小结本节课学习了：1.柱体、锥体、台体的表面积和体积公式.2.应用体积公式解决有关问题.作业习题1.3 A 组 第1、2、3题.设计感想新课标对本节内容的要求是了解棱柱、棱锥、台的表面积和体积的计算公式（不要求记忆公式），也就是说对体积和面积公式的推导、证明和记忆不作要求，按通常的理解是会求体积和面积，以及很简单的应用即可.因此本节教学设计中就体现了这一点，没有过多地在公式的推导上“纠缠不休”，把重点放在了对公式的简单应用上.由于本节图形较多，建议在使用时，尽量结合信息技术.。

1.3.1柱体、锥体、台体的表面积与体积（1课时）一、教学目标1、知识与技能（1）通过对柱、锥、台体的研究，掌握柱、锥、台的表面积和体积的求法。

（2）能运用公式求解，柱体、锥体和台全的全积，并且熟悉台体与术体和锥体之间的转换关系。

（3）培养学生空间想象能力和思维能力。

2、过程与方法（1）让学生经历几何全的侧面展一过程，感知几何体的形状。

（2）让学生通对照比较，理顺柱体、锥体、台体三间的面积和体积的关系。

3、情感与价值通过学习，使学生感受到几何体面积和体积的求解过程，对自己空间思维能力影响。

从而增强学习的积极性。

二、教学重点、难点重点：柱体、锥体、台体的表面积和体积计算难点：台体体积公式的推导三、学法与教学用具1、学法：学生通过阅读教材，自主学习、思考、交流、讨论和概括，通过剖析实物几何体感受几何体的特征，从而更好地完成本节课的教学目标。

2、教学用具：实物几何体，投影仪四、教学设想（一）、课题入导（1）教师提出问题：在过去的学习中，我们已经接触过一些几何体的面积和体积的求法及公式，哪些几何体可以求出表面积和体积？引导学生回忆，互相交流，教师归类。

（2）教师设疑：几何体的表面积等于它的展开圈的面积，那么，柱体，锥体，台体的侧面展开图是怎样的？你能否计算？引入本节内容。

（二）、探究新知（1）利用多媒体设备向学生投放正棱柱、正三棱锥和正三棱台的侧面展开图（2）组织学生分组讨论：这三个图形的表面由哪些平面图形构成？表面积如何求？（3）教师对学生讨论归纳的结果进行点评。

3、质疑答辩、排难解惑、发展思维（1）教师引导学生探究圆柱、圆锥、圆台的侧面展开图的结构，并归纳出其表面积的计算公式:r1为上底半径 r为下底半径 l为母线长（2）组织学生思考圆台的表面积公式与圆柱及圆锥表面积公式之间的变化关系。

（3）教师引导学生探究：如何把一个三棱柱分割成三个等体积的棱锥？由此加深学生对等底、等高的锥体与柱体体积之间的关系的了解。