高二数学选择性必修一导学案2.1.1倾斜角与斜率(课后练习)

2．1直线的倾斜角与斜率2．1.1倾斜角与斜率内容标准学科素养1.在平面直角坐标系中，结合具体图形，探索确定直线位置的几何要素．2.理解直线的倾斜角和斜率的概念．3.经历用代数方法刻画直线斜率的过程，掌握过两点的直线斜率的计算公式．4.掌握倾斜角与斜率的对应关系. 数学抽象直观想象逻辑推理数学运算授课提示：对应学生用书第31页[教材提炼]知识点一直线的倾斜角预习教材，思考问题如图，在平面直角坐标系中，过一点P(2,2)可以作出多少条直线？这些直线区别在哪里呢？如何表示这些直线的方向呢？[提示]无数条．区别是它们的方向不同．这些直线相对于x轴的倾斜程度不同，也就是它们与x轴所成的角不同．因此，我们可以利用这样的角来表示这些直线的方向．知识梳理定义 当直线l 与x 轴相交时，取x 轴作为基准，x 轴正向与直线l 向上的方向之间所成的角α叫做直线l 的倾斜角规定 当直线l 与x 轴平行或重合时，规定直线l 的倾斜角为0°记法 α图示范围0°≤α＜180°作用(1)表示平面直角坐标系内一条直线的倾斜程度；(2)确定平面直角坐标系中一条直线位置的几何要素是：直线上的一个定点以及它的倾斜角，二者缺一不可知识点二 直线的斜率 预习教材，思考问题我们知道：两点确定一条直线，进而它的倾斜角也就确定了，那么任给直线l 上两点P 1(x 1，y 1)，P 2(x 2，y 2)(其中x 1≠x 2)，直线l 的倾斜角α与P 1，P 2两点的坐标有什么样的内在联系呢？请用向量法探究下列问题：(1)已知直线l 经过O (0,0)，P (1,1)，α与O ，P 的坐标有什么关系？ [提示] 如图，OP →＝(1,1)，由正切函数的定义，得tan α＝1.(2)类似地，如果直线l 经过P 1(1,0)，P 2(－1,2)，α与P 1，P 2的坐标有什么关系？ [提示] 如图，P 1P 2→＝(－2,2)，平移P 1P 2→到OP →，则点P 的坐标为(－2,2)，且直线OP 的倾斜角也是α.由正切函数的定义，有tan α＝2－2＝－1.(3)一般地，如果直线l 经过两点P 1(x 1，y 1)，P 2(x 2，y 2)，x 1≠x 2，那么α与P 1，P 2的坐标有怎样的关系？[提示] 如图，当向量P 1P 2→的方向向上时，P 1P 2→＝(x 2－x 1，y 2－y 1)．平移P 1P 2→到OP →，则点P 的坐标为(x 2－x 1，y 2－y 1)，且直线OP 的倾斜角也是α.由正切函数的定义，有tan α＝y 2－y 1x 2－x 1.当向量P 2P 1→的方向向上时，P 2P 1→＝(x 1－x 2，y 1－y 2)．平移P 2P 1→到OP →，则点P 的坐标为(x 1－x 2，y 1－y 2)，且直线OP 的倾斜角也是α.如图，由正切函数的定义，也有tan α＝y 1－y 2x 1－x 2＝y 2－y 1x 2－x 1.知识梳理 (1)直线l 的倾斜角α与直线l 上的两点P 1(x 1，y 1)，P 2(x 2，y 2)(x 1≠x 2)的坐标有如下关系：tan α＝y 2－y 1x 2－x 1.(2)我们把一条直线的倾斜角α的正切值叫做这条直线的斜率．常用小写字母k 表示，即k ＝tan_α.(3)倾斜角和斜率分别从形和数两个角度刻画了直线相对于x 轴的倾斜程度，它们的对应关系：图示倾斜角(范围) α＝0° 0°＜α＜90° α＝90° 90°＜α＜180°斜率(范围)k ＞0不存在k ＜0(4)若直线l 的斜率为k ，它的一个方向向量的坐标为(x ，y )，则k ＝yx.[自主检测]1．下图中α能表示直线l 的倾斜角的是( )A ．①B ．①②C ．①③D ．②④解析：结合直线l 的倾斜角的概念可知①③可以，选C. 答案：C2．(教材P55练习2改编)在直角坐标系中，一条直线的斜率为3，则此直线的倾斜角为( )A ．30°B ．60°C ．120°D ．150°解析：由题意得tan α＝3，又0°≤α<180°，∴α＝60°. 答案：B3．(教材P55练习3改编)过点M (－3，2)、N (－2，3)的直线的斜率是( ) A ．1 B ．－1 C ．2D.32解析：过点M 、N 的直线的斜率k ＝3－2－2＋3＝1.答案：A4．若过A (4，y )，B (2，－3)两点的直线的倾斜角是45°，则y ＝________.解析：直线的倾斜角为45°，则其斜率为k ＝tan 45°＝1.由斜率公式，得－3－y 2－4＝1，解得y ＝ －1.答案：－15．已知A (1,1)，B (3,5)，C (a,7)，D (－1，b )四点在同一直线上，求直线的斜率及a 、b 的值．解析：由题意知，k AB ＝5－13－1＝2， 由k AC ＝7－1a －1＝2，解得a ＝4；由k AD ＝b －1－1－1＝2，解得b ＝－3，故直线的斜率为2，a ＝4，b ＝－3.授课提示：对应学生用书第32页探究一 求直线的倾斜角[例1] (1)设直线l 过原点，其倾斜角为α，将直线l 绕坐标原点沿逆时针方向旋转45°得到直线l 1，则直线l 1的倾斜角为( )A ．α＋45°B ．α－135°C ．135°－αD ．当0°≤α＜135°时，倾斜角为α＋45°，当135°≤α＜180°时，倾斜角为α－135° (2)设直线l 1过原点，其倾斜角α＝15°，直线l 1与l 2的交点为A ，且l 1与l 2向上的方向之间所成的角为75°，则直线l 2的倾斜角为________．[分析] 对于(1)，由于α不确定，需分情况讨论；对于(2)，画出图象，利用图象求解． [解析] (1)根据题意，画出图形，如图所示：因为0°≤α＜180°，显然A ，B ，C 未分类讨论，均不全面，不合题意．通过画图(如图所示)可知：当0°≤α＜135°，l 1的倾斜角为α＋45°；当135°≤α＜180°时，l1的倾斜角为45°＋α－180°＝α－135°.故选D.(2)设直线l2的倾斜角为α，由图可知，α＝15°＋75°＝90°，∴直线l2的倾斜角为90°.[答案](1)D(2)90°直线的倾斜角可以看作是由x轴绕着交点按逆时针方向旋转到与直线重合时所成的最小正角．所以求直线的倾斜角时，往往借助于图形．结合图形求倾斜角时，应注意倾斜角的范围以及平面几何知识的应用.1．已知直线l向上方向与y轴正向所成的角为30°，则直线l的倾斜角为________.解析：有如下两种情况：(1)如图①，直线l向上方向与x轴正向所成的角为60°，即直线l的倾斜角为60°.(2)如图②，直线l向上方向与x轴正向所成的角为120°，即直线l的倾斜角为120°.答案：60°或120°探究二根据斜率公式求斜率[例2]直线l过点P(1,0)，且与以A(2,1)，B(0，3)为端点的线段有公共点，则直线l 斜率的取值范围为________．[分析]结合图形，根据直线斜率的变化情况，确定出其范围．[解析] 如图，∵k AP ＝1－02－1＝1，k BP ＝3－00－1＝－3，∴k ∈(－∞，－ 3 ]∪[1，＋∞)． [答案] (－∞，－ 3 ]∪[1，＋∞)1．若将本例(2)中P (1,0)改为P (－1,0)，其他条件不变，求直线l 斜率的取值范围． 解析：∵P (－1,0)，A (2,1)，B (0，3)， ∴k AP ＝1－02－(－1)＝13，k BP ＝3－00－(－1)＝ 3.如图可知，直线l 斜率的取值范围为⎣⎡⎦⎤13，3. 2．若将本例(2)中的B 点坐标改为(2，－1)，其他条件不变，求直线l 倾斜角α的取值范围．解析：如图，直线P A 的倾斜角为45°，直线PB 的倾斜角为135°，由图象知l 的倾斜角的范围为 {} |α0°≤α≤45°∪{} |α135°≤α<180°.当已知两定点坐标求过这两点的直线斜率时，可直接利用斜率公式求解．应用斜率公式时，应先判定两定点的横坐标是否相等．若相等，直线垂直于x 轴，斜率不存在；若不相等，再代入斜率公式求解.探究三 斜率与倾斜角的应用[例3] 已知某直线l 的倾斜角α＝45°，又P 1(2，y 1)，P 2(x 2,5)，P 3(3,1)是此直线上的三点，求x 2，y 1的值．[分析] 直线l 的倾斜角已知可以求出其斜率且P 1、P 2、P 3均在直线l 上，故任两点的斜率均等于直线l 的斜率，从而可以解出x 2，y 1的值．[解析] ∵α＝45°，∴直线l 的斜率k ＝tan 45°＝1， ∵P 1，P 2，P 3都在直线l 上，∴kP 1P 2＝kP 2P 3＝k . ∴5－y 1x 2－2＝1－53－x 2＝1，解得：x 2＝7，y 1＝0.斜率是反映直线相对于x 轴正方向的倾斜程度的，直线上任意两点所确定的方向不变，即在同一直线上任意不同的两点所确定的斜率相等，这正是利用斜率可证三点共线的原因．2．如果三点A (2,1)，B (－2，m )，C (6,8)在同一条直线上，则m 的值为________． 解析：k AB ＝m －1－2－2＝1－m 4，k AC ＝8－16－2＝74.∵A 、B 、C 三点共线，∴k AB ＝k AC .即1－m 4＝74，∴m ＝－6.答案：－6授课提示：对应学生用书第34页一、“数缺形时少直观，形缺数时难入微”——数形结合思想在求斜率取值范围中的应用►直观想象、逻辑推理、数学抽象[典例1] 经过点P (0，－2)作直线l ，若直线与过A (－2,3)，B (2,1)的线段总没有公共点，则直线l 斜率的取值范围是________．[解析] 设直线l 的斜率为k ，直线AP 的斜率为k AP ，直线BP 的斜率为k BP ， 当直线l 与线段AB 有公共点时，k ≤k AP 或k ≥k BP ，即当直线l 与线段AB 有公共点时，k ≤3－(－2)－2－0＝－52或k ≥1－(－2)2－0＝32，所以当直线l 与线段AB 没有公共点时，－52＜k ＜32.答案：⎩⎨⎧⎭⎬⎫ |k －52<k <32二、“历史使人聪明，诗歌使人机智，数学使人精细” ——分类讨论在求倾斜角取值范围中的应用►数学运算、直观想象、逻辑推理[典例2] 求经过A (m,3)，B (1,2)两点的直线的斜率，并指出倾斜角α的取值范围． [解析] 当m ＝1时，直线的斜率不存在，此时直线的倾斜角α＝90°. 当m ≠1时，由斜率公式可得k ＝3－2m －1＝1m －1.①当m >1时，k ＝1m －1>0，所以直线的倾斜角α的取值范围是0°<α<90°. ②当m <1时，k ＝1m －1<0，所以直线的倾斜角α的取值范围是90°<α<180°.[纠错心得] 未考虑两点斜率公式运用的条件，从而忽略了m ＝1的情况．。

倾斜角与斜率【学习目标】知识目标：1．在平面直角坐标系中，结合具体图形，探索确定直线位置的几何要素。

2．理解直线的倾斜角和斜率的概念，理解它们之间的关系。

3．掌握过两点的直线斜率的计算公式。

能力目标：1．能用概念和公式解决有关问题。

2．培养学生观察、探索能力,运用数学语言表达能力,数学交流与评价能力.【学习过程】知识链接1．三角函数的定义：在直角三角形中，内α为锐角，=αsin ，=αcos ，=αtan 。

2．数轴上任意两点21,x x 间的距离公式： 一、倾斜角的概念：看一看：预习。

填一填：1．当 时，我们取 作为基准， 与直线l 之间所成 的角α叫做直线l 的倾斜角。

当 时，我们规定它的倾斜角为 0。

2．直线倾斜角的范围是 。

想一想：对于平面直角坐标系内的一条直线，它的位置由哪些条件确定呢？（结合课件演示）练一练：下列四图中，表示直线的倾斜角正确的是( )二、斜率的概念：试一试：1．类比实例坡度（比）定义斜率概念。

2．对照课本总结你对直线斜率概念的理解：想一想：斜率为正或负时，直线具有怎样的位置？(结合课件演示)记一记：当α= 0时，k 0；当 0<α<90时，k 0；当α=9 0时，k ；当90<α<180时，k 0。

练一练:心得：用到的公式k= ，tan （180α-）= 。

三、斜率公式：练一练： 已知P （1，2）、Q （3，4），求直线PQ 的倾斜角与斜率 。

想一想：如何由直线上两点的坐标计算直线的斜率。

看一看：直线P 1 P 2在平面直角坐标系内的位置情形。

（1） （2） （3） （4）记一记：已知两点,),,(),(212221,11x x y x P y x P ≠则过这两点的直线的斜率公式是说一说：你对该公式的理解： 例1 已知A （4，2），B （-8，2），C （0，2），直线AB ，BC ，CA 的斜率，并判断这些直线的倾斜角是锐角还是钝角。

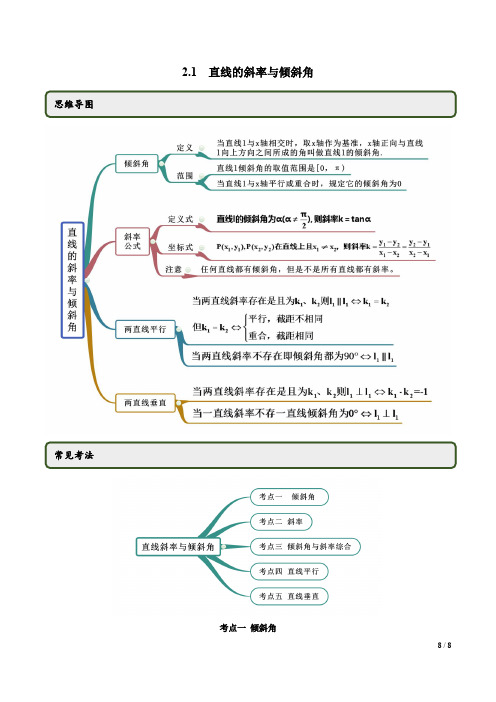
2.1 直线的斜率与倾斜角考点一倾斜角【例1】（1）（2020·四川高一期末）直线l x +y ﹣3＝0的倾斜角为（ ） A ．30°B ．60°C ．120°D ．90°（2）（2020·全国高二课时练习）l 经过第二、四象限，则直线l 的倾斜角α的范围是( ) A ．0°≤α<90° B ．90°≤α<180° C ．90°<α<180° D ．0°<α<180°【答案】（1）C （2）C【解析】直线l +y ﹣3＝0的倾斜角为α则tan k α== [0,180)α∈︒，所以120α=︒故选：C（2）由题意，可得直线l 经过第二、四象限，所以直线l 的倾斜角α的范围是90°α<<180°，故选C. 【一隅三反】1．（2020·科尔沁左翼后旗甘旗卡第二高级中学高一期末）直线310x -=的倾斜角α为（ ）． A ．30︒ B ．60︒C ．120︒D ．150︒【答案】C【解析】直线310x -=的斜率k =α，[)0,180α∈︒︒，则tan α=以120α=︒，故选：C2．（2020·广东高一期末）直线y 2-的倾斜角是（ ） A ．3πB ．4π C ．6π D ．56π 【答案】A【解析】设直线的倾斜角为[),0,ααπ∈，由题意直线的斜率k =tan k α==3πα=.故选：A.考点二 斜率【例2】（2020·全国高二课时练习）过点(A )与点(B )的直线的倾斜角为（ ） A ．45︒ B ．135︒C ．45︒或135︒D ．60︒【答案】A【解析】1AB k ===，故直线的倾斜角为45︒.故选：A.【一隅三反】1．（2020·全国高二课时练习）如果过P（-2，m）,Q（m，4）两点的直线的斜率为1，那么m的值是（）A．1B．4C．1或3D．1或4【答案】A【解析】由题意，过过P（-2，m）,Q（m，4）两点的直线的斜率为1，根据直线的斜率公式，可得41(2)mm-=--，解得1m=.故选：A.2．（2020·湖南天心.长郡中学高一月考）直线l经过()2,1A，()2(,)1B m m R∈两点，那么直线l的倾斜角的取值范围为（）A．0,B．30,,44πππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦C．0,4⎡⎤⎢⎥⎣⎦πD．0,,42πππ⎡⎤⎛⎫⎪⎢⎥⎣⎦⎝⎭【答案】D【解析】直线l的斜率为2212121121y y mk mx x--===---，因为m R∈，所以(],1k∈-∞，所以直线的倾斜角的取值范围是0,,42πππ⎡⎤⎛⎫⎪⎢⎥⎣⎦⎝⎭.故选：D.3．（2019·浙江下城.杭州高级中学高二期中）若直线l的倾斜角α满足23πα<<，且2πα≠，则其斜率k满足（）A．0k<<B．k>C．0k>或k<D．0k>或3k<-【答案】Ctanθ.【解析】斜率tan k α=，因为203πα<<，且2πα≠， 故tan 0α>或tan α<，即0k >或k < C.考点三 倾斜角与斜率综合运用【例3】（2020·江苏省海头高级中学高一月考）已知点(2,1),(3,)A B m -，若13m ⎡⎤∈--⎢⎥⎣⎦，则直线AB 的倾斜角的取值范围为（ ）A ．5,36ππ⎡⎤⎢⎥⎣⎦B ．50,,36πππ⎡⎤⎡⎫⎪⎢⎥⎢⎣⎦⎣⎭C ．5,,3226ππππ⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦D ．5,,326ππππ⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭【答案】B【解析】因为(2,1),(3,)A B m -，所以()1132AB m k m --==+-，因为13m ⎡⎤∈--⎢⎥⎣⎦，所以13m⎡+∈-⎢⎣，设倾斜角为α，[)0,απ∈，则t an 3α⎡∈-⎢⎣，所以50,,36ππαπ⎡⎤⎡⎫∈⎪⎢⎥⎢⎣⎦⎣⎭.故选：B【一隅三反】1．（2020·全国高二课时练习）直线l 过点()1,0P ，且与以()2,1A ，(B 为端点的线段有公共点，求直线l 的斜率和倾斜角的取值范围.【答案】斜率的范围：([),1,-∞⋃+∞；倾斜角的范围：45120θ︒≤≤︒. 【解析】如图所示.∵10121AP k -==-，001BP k ==-，又直线l 过点()1,0P ，且与以()2,1A ，(B 为端点的线段有公共点，所以由图像可得：([),1,k ∈-∞+∞，因此倾斜角的范围为：45120θ︒≤≤︒.2．（2020·全国高二课时练习）已知直线l 过点()1,1M m m +-，()2,1N m . （1）当m 为何值时，直线l 的斜率是1？ （2）当m 为何值时，直线l 的倾斜角为90︒？【答案】（1）m =32；（2）m =1. 【解析】（1）由题意，1121121MN m m k m m m ---===+--，解得32m =； （2）若直线l 的倾斜角为90︒，则l 平行于y 轴，所以12m m +=，得1m =.3．（2020·哈尔滨市第一中学校高一期末）已知直线l 过点(1,0)P 且与以(2,1)A ，(4,3)B -为端点的线段AB 有公共点，则直线l 倾斜角的取值范围为_______． 【答案】30,,44πππ⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭【解析】如图所示：设直线l 过A 点时直线l 的斜率为1k ，直线l 过B 点时直线l 的斜率为2k ，则，110121k -==-，230141k --==--， 所以要使直线l 与线段AB 有公共点，则直线l 的斜率的取值范围为：[]1,1-, 所以l 倾斜角的取值范围30,,44πππ⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭.故答案为：30,,44πππ⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭. 考点四 直线平行【例4】（2020·四川达州.高三其他（文））直线12:0l ax y a ++=与直线20:2l x ay a +-=互相平行，则实数a =（ ） A ．4- B ．4C ．2-D ．2【答案】D【解析】当0a =时，1:0l y =，2:0l x =，此时12l l ⊥，不满足条件， 当0a ≠时，应满足22aaa a，解得2a =，综上，2a =.故选：D.【一隅三反】1．（2020·黑龙江高一期末）若直线2x +（a +2）y +4＝0与直线（a ﹣1）x +2y +2＝0平行，则实数a 的值为（ ） A ．﹣3 B ．2 C ．2或﹣3 D ．23-【答案】A【解析】∵ 直线2(2)40x a y +++=与直线(1)220a x y -++=平行， ∴ (2)(1)22a a +-=⨯，解得：2a =或3a =-，当2a =时，直线2440x y ++=与直线220x y ++=重合，∴2a =舍去；当3a =-时，直线240x y -+=与直线4220x y -++=平行，∴3a =-成立.故选：A.2．（2020·江苏淮安。

新教材高中数学北师大版选择性必修第一册：1．1 一次函数的图象与直线的方程 1．2 直线的倾斜角、斜率及其关系必备知识基础练知识点一直线的倾斜角与斜率1.直线x ＝1的倾斜角和斜率分别是( )A ．45°，1B ．135°，－1C ．90°，不存在D ．180°，不存在2．若直线l 的向上方向与y 轴的正方向成30°角，则直线l 的倾斜角为( ) A ．30° B．60°C．30°或150° D．60°或120°3．如图，直线l 1，l 2，l 3的斜率分别为k 1，k 2，k 3，则( ) A ．k 1<k 2<k 3B ．k 3<k 1<k 2 C ．k 3<k 2<k 1D ．k 1<k 3<k 24．若两直线的斜率互为相反数，则它们的倾斜角的关系是________.知识点二直线的斜率公式5.已知直线l 经过点A (0，－1)，B (1，1)，则直线l 的斜率是( ) A ．2 B ．－2C ．12 D ．－126．求经过A (m ，3)，B (1，2)两点的直线的斜率，并指出倾斜角α的取值范围．知识点三斜率公式的应用7.若点P (x ，y )在函数y ＝2x ＋1(－2≤x ≤2)的图象上运动，则y x的取值范围是( ) A ．⎣⎢⎡⎭⎪⎫52，＋∞ B ．⎝ ⎛⎦⎥⎤－∞，32C ．⎣⎢⎡⎦⎥⎤32，52 D ．⎝ ⎛⎦⎥⎤－∞，32∪⎣⎢⎡⎭⎪⎫52，＋∞ 8．设点A (m ，－m ＋3)，B (2，m －1)，C (－1，4)，若直线AC 的斜率等于直线BC 的斜率的3倍，则实数m 的值为________.9．若A (2，2)，B (a ，0)，C (0，b )(ab ≠0)三点共线，求1a ＋1b的值．关键能力综合练一、选择题1．已知直线l 的斜率的绝对值为1，则直线l 的倾斜角为( ) A ．45° B．135°C．45°或135° D．全不对2．已知l 1⊥l 2，直线l 1的倾斜角为60°，则直线l 2的倾斜角为( ) A ．60° B．120° C ．30° D．150°3．以下两点确定的直线的斜率不存在的是( ) A ．(4，2)与(－4，1) B ．(0，3)与(3，0)C ．(3，－1)与(2，－1)D ．(－2，2)与(－2，5)4．已知直线PQ 的斜率为－3，将该直线绕点P 顺时针旋转60°，所得的直线的斜率是( )A ．0B ．33C ． 3D ．－ 3 5．已知直线经过点A (a ，4)，B (2，－a )，且斜率为4，则a 的值为( ) A ．－6 B ．－145C ．45D ．46．[易错题]直线l 经过点A (1，2)，与x 轴交点的横坐标的取值范围是(－3，3)，则其斜率的取值范围是( )A ．⎝⎛⎭⎪⎫－1，15 B ．(－∞，－1)∪⎝ ⎛⎭⎪⎫12，＋∞C ．(－∞，－1)∪⎝ ⎛⎭⎪⎫15，＋∞ D ．⎝⎛⎭⎪⎫－∞，12∪(1，＋∞)二、填空题7．直线l 过点A (1，2)，且不过第四象限，则直线l 的斜率的取值范围是________. 8．已知斜率为12的直线经过A (3，5)，B (x ，－1)，C (7，y )三点，则x ，y 的值分别为________.9．已知点A (1，2)，若在坐标轴上有一点P ，使直线PA 的倾斜角为135°，则点P 的坐标为________.三、解答题10．[探究题]已知A (1，1)，B (3，5)，C (a ，7)，D (－1，b )四点在同一条直线上，求直线的斜率k 及a ，b 的值．学科素养升级练1．[多选题]下列说法不正确的是( ) A ．任何一条直线都有唯一的倾斜角B ．若直线的倾斜角为α，则其斜率为tan αC ．直线的倾斜角越大，它的斜率越大D ．直线的斜率越大，它的倾斜角越大2．已知点A (2，－3)，B (－3，－2)，直线l 过点P (1，1)，且与线段AB 相交，则直线l 的斜率k 的取值范围是________.3．[学科素养——数学运算]已知一条光线从点A (－1，3)出发，射在x 轴上又反射出去，反射光线经过点B (2，7)，求x 轴上光照点的坐标．1．1 一次函数的图象与直线的方程1．2 直线的倾斜角、斜率及其关系必备知识基础练1．解析：∵直线x ＝1与y 轴平行，∴倾斜角为90°，斜率不存在． 答案：C2．解析：如图，直线l 有两种情况，故l 的倾斜角为60°或120°.答案：D3．解析：由题图可知，直线l 1的倾斜角为钝角，所以k 1<0；直线l 2与直线l 3的倾斜角为锐角，且直线l 2的倾斜角较大，所以k 2>k 3>0，所以k 2>k 3>k 1.答案：D4．解析：两直线的斜率互为相反数，则它们的倾斜角互补． 答案：互补5．解析：因为直线l 经过点A (0，－1)，B (1，1)，所以直线l 的斜率为1－（－1）1－0＝2，故选A.答案：A6．解析：当m ＝1时，直线的斜率不存在，此时直线的倾斜角α＝90°.当m ≠1时，由斜率公式可得k AB ＝3－2m －1＝1m －1.①当m >1时，k ＝1m －1>0，所以直线的倾斜角的取值范围是0°<α<90°. ②当m <1时，k ＝1m －1<0，所以直线的倾斜角的取值范围是90°<α<180°. 综上，当m ＝1时，斜率不存在，α＝90°；当m >1时，斜率k ＝1m －1，0°<α<90°；当m <1时，斜率k ＝1m －1，90°<α<180°.7．解析：已知函数y ＝2x ＋1(－2≤x ≤2)的图象是一条线段，设为AB ，其中A (2，5)，B (－2，－3).yx的几何意义是线段AB 上的任意一点P (x ，y )与坐标原点O (0，0)连线的斜率，易得k OA ＝52，k OB ＝32，根据图象可知，y x 的取值范围是⎝ ⎛⎦⎥⎤－∞，32∪⎣⎢⎡⎭⎪⎫52，＋∞. 答案：D8．解析：依题意知直线AC 的斜率存在，则m ≠－1，由k AC ＝3k BC 得－m ＋3－4m －（－1）＝3×m －1－42－（－1），所以m ＝4.答案：49．解析：由题意可知直线AB ，AC 的斜率存在，∴a ≠2.由k AB ＝k AC 得2－02－a ＝2－b2－0，即a＋b ＝12ab ，又ab ≠0，∴1a ＋1b ＝12.关键能力综合练1．解析：设倾斜角为α，则由题意知tan α＝±1，又0°≤α<180°，所以当tan α＝1时，α＝45°；当tan α＝－1时，α＝135°.故选C.答案：C 2．解析：当两直线互相垂直时，这两条直线的倾斜角相差90°，由l 1的倾斜角为60°，知l 2的倾斜角为150°.答案：D3．解析：两点(－2，2)，(－2，5)的横坐标相同，因此过此两点的直线斜率不存在． 答案：D 4．解析：直线PQ 的斜率为－3，则其倾斜角为120°，该直线绕点P 顺时针旋转60°，倾斜角变为60°，故其斜率为 3.答案：C5．解析：∵A (a ，4)，B (2，－a )，且斜率为4，∴k AB ＝－a －42－a ＝4，解得a ＝4.答案：D6．解析：过定点A 的直线经过点B (3，0)时，直线l 与x 轴交点的横坐标为3，此时k ＝2－01－3＝－1；过定点A 的直线经过点C (－3，0)时，直线l 与x 轴交点的横坐标为－3，此时k ＝2－01＋3＝12.数形结合(如图所示)可知满足条件的直线l 的斜率的取值范围为(－∞，－1)∪⎝ ⎛⎭⎪⎫12，＋∞.答案：B7．解析：如图，当直线l 在l 1位置时，k ＝tan0°＝0；当直线l 在l 2位置时，k ＝2－01－0＝2，故直线l 的斜率的取值范围是[0，2].答案：[0，2]8．解析：由题意可知k AB ＝k AC ＝12，即5＋13－x ＝y －57－3＝12，解得x ＝－9，y ＝7.答案：－9 79．解析：由题意知k PA ＝－1.设x 轴上点P 1(m ，0)，y 轴上点P 2(0，n )满足题意．由0－2m －1＝n －20－1＝－1，得m ＝n ＝3.所以点P 的坐标为(3，0)或(0，3). 答案：(3，0)或(0，3) 10．解析：由题意可知k AB ＝5－13－1＝2，k AC ＝7－1a －1＝6a －1，k AD ＝b －1－1－1＝b －1－2，所以6a －1＝b －1－2＝2，解得a ＝4，b ＝－3，所以直线的斜率k ＝2，a ＝4，b ＝－3.学科素养升级练1．解析：由直线的倾斜角的定义知A 正确；当α≠90°时，斜率k ＝tan α，当α＝90°时，斜率不存在，故B 错误；135°>45°，但k 1＝tan135°<k 2＝tan45°，故C 错误；k 1＝－1<k 2＝1，但α1＝135°>α2＝45°，故D 错误．故选BCD.答案：BCD2．解析：如图所示，过点P 作直线PC ⊥x 轴交线段AB 于点C ，作出直线PA ，PB .①直线l 与线段AB 的交点在线段AC (除去点C )上时，直线l 的倾斜角为钝角，斜率的范围是k ≤k PA .②直线l 与线段AB 的交点在线段BC (除去点C )上时，直线l 的倾斜角为锐角，斜率的范围是k ≥k PB .因为k PA ＝－3－12－1＝－4，k PB ＝－2－1－3－1＝34，所以直线l 的斜率k 满足k ≥34或k ≤－4.答案：(－∞，－4]∪⎣⎢⎡⎭⎪⎫34，＋∞3．解析：设点A 关于x 轴的对称点为A ′，则A ′(－1，－3)，连接A ′B ，与x 轴交于点C ，则点C 即为光照点．不妨设C (a ，0)，由题意可知A ′，B ，C 三点共线，∴k A ′C ＝k BC ，即0－（－3）a －（－1）＝0－7a －2，解得a ＝－110.∴x 轴上光照点的坐标为⎝ ⎛⎭⎪⎫－110，0.。

2.2 直线及其方程2.2.1 直线的倾斜角与斜率课后训练巩固提升1.已知直线l 过点P(-2,a),Q(a,4).若直线l 的斜率为1,则a 的值为( ) A.1 B.4 C.1或4 D.1或-4解析:k PQ =a -4-2-a=1,解得a=1.答案:A2.若斜率为3a-1的直线的倾斜角是钝角,则实数a 的取值范围是( ) A.(-∞,13)B.(13,+∞) C.(3,+∞)D.(-∞,3)解析:由已知,得3a-1<0,解得a<13. 答案:A3.设点P 在y 轴上,点M 与点N 关于y 轴对称,若直线PM 的斜率为2,则直线PN 的斜率为( ) A.2B.-2C.12D.-12解析:设P(0,y 0),M(a,b),则N(-a,b).∵k PM =y 0-b 0-a=2,∴y 0-b a=-2,∴k PN =y 0-b0-(-a )=-2.答案:B4.已知斜率为2的直线经过点(3,5),(a,7),(-1,b),则a,b 的值为( ) A.a=4,b=0B.a=-4,b=-3C.a=4,b=-3D.a=-4,b=3 解析:由已知,得7-5a -3=b -5-1-3=2,解得a=4,b=-3.答案:C5.(多选题)下列关于斜率和倾斜角的说法正确的是( ) A.任意一条直线都有唯一的斜率和倾斜角 B.一条直线的倾斜角可以为-π6C.倾斜角为0的直线只有一条,即x 轴D.若一条直线的倾斜角为α,则sin α∈[0,1] 答案:AD6.已知斜率为-13的直线上有P(m,3),Q(1,2)两点,则实数m= ,该直线的一个方向向量为 ;一个法向量为 .解析:由已知,得3-2m -1=-13,解得m=-2.a=(1,-13),b=(13,1)分别为该直线的一个方向向量和一个法向量.答案:-2 (1,-13) (13,1)(后两空的答案不唯一)7.过原点作直线l,使l 与连接A(1,1)和B(1,-1)两点的线段相交,则直线l 的倾斜角θ的取值范围是 . 答案:[0,π4]∪[3π4,π)8.已知点M(5,3)和点N(-3,2),若直线PM 和PN 的斜率分别为2和-74,则点P 的坐标为 . 解析:设P(x,y),则y -3x -5=2,y -2x+3=-74,解得x=1,y=-5,故P(1,-5). 答案:(1,-5)9.已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA 的斜率,并判断这些直线的倾斜角是锐角还是钝角. 解:直线AB 的斜率k AB =1-2-4-3=17.直线BC 的斜率k BC =-1-10-(-4)=-12.直线CA 的斜率k CA =-1-20-3=1.由k AB >0,k CA >0知,直线AB 与CA 的倾斜角均为锐角; 由k BC <0知,直线BC 的倾斜角为钝角.10.已知点A(3,4),在坐标轴上有一点B,使得直线AB的斜率为2,求出点B 的坐标.=2,解解:若点B在x轴上,则可设B(x0,0),x0≠3.则直线AB的斜率k=0-4x0-3得x0=1,即B(1,0).若点B在y轴上,则可设B(0,y0),y0≠4.则直线AB的斜率k=y0-4=2,解得y0=-2,即B(0,-2).故点B的坐标为(1,0)或(0,-2).0-31.若直线l的一个方向向量与y轴的正方向成60°角,则直线l的倾斜角为( )A.30°B.60°C.30°或150°D.60°或120°答案:C2.若直线l过点A(1,2),且不过第四象限,则直线l的斜率k的最大值是( )D.2A.0B.1C.12解析:如图,过点A作直线l与x轴平行,将直线l绕点A按逆时针方向旋转,可知当直线l过点O时,l的斜率k取最大值,此时k=2.答案:D3.(多选题)已知直线l 1的斜率为1,直线l 2的斜率为a,其中a 为实数,当两直线的夹角在区间(0,π12)内变动时,a 的取值可能是( )A.√32B.2√33C.√3D.√34解析:由题意可知,l 1的倾斜角为π4,则l 2的倾斜角的取值范围为(π6,π4)∪(π4,π3),故a 的取值范围为(√33,1)∪(1,√3). 故选项A,B 符合题意. 答案:AB4.若三点A(0,2),B(2,5),C(3,b)能作为三角形的三个顶点,则实数b 满足的条件是 . 解析:由题意可知,k AB ≠k AC ,即5-22-0≠b -23-0,故b≠132.答案:b≠1325.已知直线l 1的倾斜角α1=15°,直线l 1与l 2的交点为A,若直线l 2绕点A 按逆时针方向旋转60°后与直线l 1重合,则直线l 2的斜率为 .解析:如图,设直线l 2的倾斜角为α2,则由题意知,180°-α2+15°=60°, 解得α2=135°.故k=tanα2=tan135°=-1. 答案:-16.已知一条光线从点A(-2,3)射入,经x 轴上点P 反射后,反射出的光线通过点B(5,7),求点P 的坐标.解:由已知,得点A(-2,3)关于x 轴的对称点为A'(-2,-3).根据题意可知,P,A',B 三点共线,故k PA'=k A'B . 设P(x,0),则-3-0-2-x=-3-7-2-5,解得x=110.故点P 的坐标为(110,0).7.已知直线l 经过A(-1,m),B(m,1)两点,问:当m 取何值时,(1)l 与x 轴平行;(2)l 与y 轴平行;(3)l 的斜率为13;(4)l 的一个法向量为a=(3,2)?解:(1)当直线l 与=1.(2)当直线l 与y 轴平行时,A,B 两点的横坐标相等,故m=-1. (3)由k AB =1-m m+1=13,得m=12.(4)由题意可知,AB ⃗⃗⃗⃗⃗ =(m+1,1-m),AB ⃗⃗⃗⃗⃗ ⊥a, 故3(m+1)+2(1-m)=0,解得m=-5.。

2.1.1 倾斜角与斜率【学习目标】1.直线的倾斜角当直线l与x轴相交时，我们取作为基准，x轴正向与直线l方向之间所成的角α叫做直线l的倾斜角．直线的倾斜角α的取值范围是{}，并规定与x轴平行或重合的直线的倾斜角为．注意三个条件：①x轴正向；①直线向上的方向；①小于180°的非负角．2.斜率的概念及斜率公式定义：倾斜角α(α≠90°)的．记法：k＝．3.斜率与倾斜角的对应关系其对应情况如下表所示．4.斜率公式经过两点P 1(x 1，y 1)，P 2(x 2，y 2)(x 1≠x 2)的直线的斜率公式：k ＝ ． 注意：当x 1＝x 2时，斜率不存在．【小试牛刀】1．只给出一个倾斜角能确定一条直线吗？2．当一条直线的倾斜角为0°时，这条直线一定与x 轴平行吗？3.如图所示，直线l 的倾斜角为( ) A ．45°B ．135°C ．0°D ．不存在4．已知一条直线的倾斜角α＝45°，则该直线的斜率等于( ) A.22 B ．－22 C ．1 D ．－1【经典例题】题型一 直线的倾斜角 例1 下列命题正确的是( )A ．两条不重合的直线，如果它们的倾斜角相等，那么这两条直线平行B ．若一条直线的倾斜角为α，则此直线的斜率为tan αC ．若α，2α，3α分别为三条直线的倾斜角，则α的度数可以大于60°D ．若α是直线l 的倾斜角，且tan α＝22，则α＝45°[跟踪训练] 1 (1)已知直线l 的倾斜角为θ－25°，则角θ的取值范围为( ) A.25°≤θ<155° B.－25°≤θ<155° C.0°≤θ<180°D.25°≤θ<205°（2）已知直线l 向上方向与y 轴正向所成的角为30°，则直线l 的倾斜角为________.题型二 直线斜率的运算例2 （1）（利用斜率定义）若直线的倾斜角为60°，则直线的斜率为( )A. 3 B ．－ 3 C.33 D ．－33 （2）（利用斜率公式）经过下列两点的直线的斜率是否存在？如果存在，求其斜率，并确定直线的倾斜角α.①A(2,3)，B(4,5)；①C(－2,3)，D(2，－1)；①P(－3,1)，Q(－3,10).[跟踪训练] 2 (1)若直线的倾斜角为60°，则直线的斜率为()A. 3B.－ 3C.33 D.－33(2)已知过A(3,1)，B(m，－2)的直线的斜率为1，则m的值为________.题型三利用数形结合求倾斜角或斜率范围涉及直线与线段有交点问题常利用数形结合及公式求解.例3 已知两点A(－3，4)，B(3，2)，过点P(1，0)的直线l与线段AB有公共点．(1)求直线l的斜率k的取值范围；(2)求直线l的倾斜角α的取值范围．[跟踪训练] 3 直线l过点P(1,0)，且与以A(2,1)，B(0，3)为端点的线段有公共点，求直线l 的斜率和倾斜角的取值范围.题型四直线的斜率的应用例4 已知实数x，y满足y＝－2x＋8，且2≤x≤3，求yx的最大值和最小值．例5 已知三点A(0,1)，B(1,3)，C(2,5)，求证：A，B，C三点共线.[跟踪训练] 4如果三点A(2,1)，B(－2，m)，C(6,8)在同一条直线上，求实数m的值.【当堂达标】1．对于下列命题：①若α是直线l的倾斜角，则0°≤α<180°；①若k是直线的斜率，则k①R；①任一条直线都有倾斜角，但不一定有斜率；①任一条直线都有斜率，但不一定有倾斜角．其中正确命题的个数是()A．1 B．2 C．3 D．42.若经过A(m,3)，B(1,2)两点的直线的倾斜角为45°，则m等于()A.2B.1C.－1D.－23．一条直线的斜率等于33，则此直线的倾斜角等于________．4．已知点A(1，2)，若在坐标轴上有一点P，使直线P A的倾斜角为135°，则点P的坐标为________．5.求经过A(m,3)，B(1,2)两点的直线的倾斜角α的取值范围是________.(其中m≥1)6．求经过下列两点的直线的斜率，并判断其倾斜角是锐角还是钝角．(1)(1，1)，(2，4)；(2)(－3，5)，(0，2)；(3)(2，3)，(2，5)；(4)(3，－2)，(6，－2)．7．已知三点A(1,3)，B(5,11)，C(－3，－5)，求证：这三点在同一条直线上．【参考答案】【自主学习】1.x轴向上α|0°≤α＜180° 0°2.正切值tan__α3.90° k＝0 k>0 k<04.y2－y1 x2－x1【小试牛刀】1.不能．倾斜角只能确定直线的方向，要确定直线还需知道直线上的一个点．2.不一定，也可能与x轴重合．3.B4. C 解析k＝tan α＝tan 45°＝1.【经典例题】例1 A 解析0°≤α＜180°，当α＝90°，此时直线不存在斜率，B错；α＝60°时，3α＝180°，C错；tan 45°＝1，D错．[跟踪训练] 1 （1）D 解析因为直线l的倾斜角为θ－25°，所以0°≤θ－25°<180°，所以25°≤θ<205°.（2）60°或120° 解析有两种情况：①如图(1)，直线l向上方向与x轴正向所成的角为60°，即直线l的倾斜角为60°.①如图(2)，直线l向上方向与x轴正向所成的角为120°，即直线l的倾斜角为120°.例2 （1）A 解析k＝tan 60°＝ 3.（2）解①存在.直线AB的斜率k AB＝5－34－2＝1，即tan α＝1，又0°≤α<180°，所以倾斜角α＝45°.①存在.直线CD的斜率k CD＝－1－32－－2＝－1，即tan α＝－1，又0°≤α<180°，所以倾斜角α＝135°.①不存在.因为x P＝x Q＝－3，所以直线PQ的斜率不存在，所以倾斜角α＝90°. [跟踪训练] 2 （1）A解析利用斜率的定义计算（2）0 解析由斜率公式计算斜率例3 解如图所示，由题意，知k P A＝4－0－3－1＝－1，k PB＝2－03－1＝1.(1)要使直线l与线段AB有公共点，则直线l的斜率k的取值范围是k≤－1或k≥1.(2)由题意可知直线l的倾斜角介于直线PB与P A的倾斜角之间，又PB的倾斜角是45°，P A的倾斜角是135°，所以α的取值范围是45°≤α≤135°.[跟踪训练] 3 解如图所示.①k AP＝1－02－1＝1，k BP＝3－00－1＝－3，①k①(－∞，－3]①[1，＋∞)，①45°≤α≤120°.例4 解如图所示，由于点(x，y)满足关系式2x＋y＝8，且2≤x≤3，可知点P(x，y)在线段AB 上移动，并且A，B两点的坐标可分别求得为(2，4)，(3，2)．由于yx的几何意义是直线OP的斜率，且k OA＝2，k OB＝23，所以可求得yx的最大值为2，最小值为23.例5 证明①k AB＝3－11－0＝2，k BC＝5－32－1＝2，①k AB＝k BC，①A，B，C三点共线.[跟踪训练] 4 解 k AB ＝m －1－2－2＝1－m 4，k AC ＝8－16－2＝74，①A ，B ，C 三点共线，①k AB ＝k AC ，即1－m 4＝74，①m ＝－6. 【当堂达标】1. C 解析 ①①①正确．2. A 解析 由题意知，tan 45°＝2－31－m，得m ＝2. 3. 30° 解析 k ＝tan α＝33，又0°≤α＜180°，故α＝30°.4. (3，0)或(0，3) 解析 由题意知k P A ＝－1，若P 点在x 轴上，则设P (m ，0)，则0－2m －1＝－1，解得m ＝3；若P 在y 轴上，则设P (0，n )，则n －20－1＝－1，解得n ＝3；故P 点的坐标为(3，0)或(0，3)．5. 0°<α≤90° 解析 当m ＝1时，倾斜角α＝90°；当m >1时，tan α＝3－2m －1>0，①0°<α<90°.故0°<α≤90°. 6.解 (1)k ＝4－12－1＝3>0，所以倾斜角是锐角； (2)k ＝2－50－（－3）＝－1<0，所以倾斜角是钝角；(3)由x 1＝x 2＝2得：k 不存在，倾斜角是90°； (4)k ＝－2－（－2）6－3＝0，所以倾斜角为0°.7．证明：由斜率公式，得k AB ＝11351--＝2，k AC ＝5331----＝2， ①k AB ＝k AC ，且AB 与AC 都过点A ， ①直线AB ，AC 斜率相同，且过同一点A ， ∴A ，B ，C 这三点在同一条直线上．。

直线的倾斜角与斜率【学习目标】1．了解在直角坐标系中，确定直线位置的几何要素。

2．理解直线的倾斜角和斜率的概念直线的。

3．掌握过两点的斜率的计算公式。

【学习重难点】重点：直线的倾斜角和斜率的概念。

难点：直线的倾斜角与斜率的关系。

【学习过程】一、知识链接1．在直角坐标系中,只知道直线上的一点,能不能确定一条直线呢?2．在日常生活中,我们常说这个山坡很陡峭, 有时也说坡度,这里的陡峭和坡度说的是山坡与水平面之间的一个什么关系呢?二、教材助读1．直线的倾斜角（1）在直角坐标系中，确定直线位置的几何要素有（2）倾斜角的定义是（3）当直线与x轴平行或重合时,我们规定它的倾斜角为度（4）直线倾斜角的范围为试试：请描出下列各直线的倾斜角函数y=x的图像的倾斜角为 , y=-x的图像的倾斜角为 , 直线x=1倾斜角为 ,直线y=0倾斜角为2．直线的斜率（1）在日常生活中，我们经常用“升高量与前进量的比”表示“坡度”，则坡度的公式是怎样的？（2）斜率的定义:一条直线的倾斜角a (α≠900) 的正切值叫做这条直线的斜率,记为k=tan a试试：已知各直线倾斜角，则其斜率的值为α=0°时，则k0°<α< 90°,则kα= 90°，,则k90 °<α< 180°，则k3．过两点的直线斜率的公式（1）由直线上两点),(11y x A 、),(22y x B 来求直线的斜率k 的公式是：当21x x ≠时，k=当x 1=x 2 时, k（2）如果1212,x x y y ≠= 则直线与x 轴 k=如果1212,x x y y =≠ 则直线与x 轴 倾斜角等于 k（3）直线的斜率与所选择直线上两点的位置有无关系？顺序有无关系？预习自测1．已知直线的倾斜角，求直线的斜率（１） 30=α（２） 135=α（３） 90=α2．已知直线的斜率求直线的倾斜角（１）0=k （２）1=k （３）3-=k （４）k 不存在。

2.1直线的斜率与倾斜角（精练）1．（2023春·上海宝山）在下列四个命题中，正确的是（）A ．若一条直线的斜率为tan α，则此直线的倾斜角为αB ．若一条直线的倾斜角为α，则此直线的斜率为tan αC ．坐标平面内的任何一条直线均有倾斜角和斜率D ．直线的倾斜角的取值范围是[)0,π【答案】D【解析】对于A ，直线y x =的斜率为1，而5πtan14=，显然5π4不是直线y x =的倾斜角，A 错误；对于B ，直线1x =的倾斜角为π2，而直线1x =的斜率不存在，B 错误；对于C ，坐标平面内的任何一条直线均有倾斜角，而垂直于x 轴的直线没有斜率，C 错误；对于D ，直线的倾斜角的取值范围是[)0,π，D 正确.故选：D2（2022秋·高二课时练习）已知直线l 的一个方向向量为()AB = ，则直线l 的倾斜角α=（）A ．30B ．60C ．120D ．150【答案】C【解析】因为直线l 的一个方向向量为()AB =，所以直线l 的斜率tank α==又因为0180α≤< ，所以120α= ，故选：C.3．（2023·全国·高二专题练习）如图，已知直线123,,l l l 的斜率分别为123,,k k k ，则（）A ．123k k k <<B ．312k k k <<C ．321k k k <<D ．132k k k <<【答案】D【解析】设直线123,,l l l 的倾斜角分别为123,,ααα，由题图知，直线1l 的倾斜角1α为钝角，10k ∴<.又直线23,l l 的倾斜角23,αα均为锐角，且23αα>，320k k ∴<<，132k k k ∴<<.故选：D.4．（2022秋·吉林白城·高二统考期末）已知直线l 经过A ，B 两点，则l 的倾斜角为（）A ．6πB ．3πC ．23πD ．56π【答案】C【解析】设直线l 的倾斜角为θ，则tan 45k θ===-[)0,θπ∈，所以23πθ=．故选：C ．5．（2023·全国·高一专题练习）过点P (-2，m )，Q (m ，4)的直线的斜率为1，那么m 的值为（）A ．1或4B ．4C ．1或3D ．1【答案】D【解析】因为直线过点P (-2，m )，Q (m ，4)，且斜率为1所以412mk m -==+，解得1m =，故选：D 6．（2023·安徽六安·高二校考阶段练习）若过点()3,4A ，()6,3Q a 的直线的倾斜角为锐角，则实数a 的取值范围为（）A ．43a <B ．43a ≤C ．43a >D ．43a ≥【答案】C【解析】因为直线AQ 的斜率344633a k a -==--，又因为直线AQ 的倾斜角为锐角，所以403a ->，解得43a >.故选：C 7．（2023春·上海浦东新·高二上海师大附中校考阶段练习）已知直线l 的倾斜角为α，斜率为k ，那么“1k >”是“π4α>”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A【解析】由直线的斜率1k >可得tan 1α>，解得ππ24α>>，所以“1k >”是“π4α>”的充分不必要条件，故选：A8．（2023秋·江苏连云港·高二校考期末）经过点()0,1P -作直线l ，且直线l 与连接点()1,2A -，()2,1B 的线段总有公共点，则直线l 的倾斜角α的取值范围是（）A ．π3π[,]44B ．π3π[0,][,π)44⋃C ．3π[0,[)2π,π4⋃D ．3π[0,4【答案】B【解析】由题知，直线l 的倾斜角为α，则[)0,πα∈，12101PA k -+==-- ，11102PB k --==-，且直线l 与连接点()1,2A -，()2,1B 的线段总有公共点，如下图所示，则tan PA PB k k α≤≤，即ta 11n α-≤≤，α∴∈π3π[0,][,π)44⋃.故选：B9．（2022秋·安徽六安·高二校考阶段练习）已知()2,0A ，()4,4B ，若(),Q m n 在线段AB 上，则43m n -的最小值为（）A ．8-B ．8C ．4-D ．4【答案】D【解析】因为点(),Q m n 在线段AB 上，所以AB AQ k k =，且[]2,4m ∈，即400422n m --=--，所以24n m =-，设()434324212z m n m m m =-=--=-+，所以当4m =时，min 24124z =-⨯+=.故选：D.10．（2022秋·北京·高二人大附中校考阶段练习）已知点()1,2A -和点()2,1B ，经过点()0,1P -作直线l ，若直线l 与射线AB 有公共点，则直线l 的斜率的取值范围是（）A ．[1,3)-B ．(,1](3,)-∞-⋃+∞C ．[1,1]-D ．(,1][1,)∞∞--⋃+【答案】A【解析】如图已知点()1,2A -,()2,1B ，()0,1P -则1(2)321AB k --==-，1(2)101AP k ---==--若经过点()0,1P -的直线l 与射线AB 有公共点，则直线l 的斜率的取值范围是[)1,3-故选：A11．（2022秋·江苏苏州·高二江苏省苏州实验中学校考阶段练习）已知直角坐标系中()()()1,1,2,3,4,2A B C -，连接两点的所有直线中倾斜角最大的直线的斜率为（）A ．2B ．1-C ．43D ．52-【答案】B 【解析】因为31221AB k -==-，21141AC k --==--，()325242BC k --==--，而tan k α=在π0,2⎡⎫⎪⎢⎣⎭上单调递增，且0k >，在π,π2⎛⎫⎪⎝⎭上递增，且0k <，512->-，所以连接两点的所有直线中倾斜角最大的直线为AC ，其斜率为1-．故选：B ．12．（2023·甘肃兰州）已知()2,3A -，()3,2B --，()1,1P ，直线l 过点B ，且与线段AP 相交，则直线l 的斜率k 的取值范围是（）A ．4k ≤-或34k ≥B ．1354k -≤≤C ．34k ≤-或4k ≥D ．15k ≤-或34k ≥【答案】B【解析】如图所示：由题意得，所求直线l 的斜率k 满足BP BA k k k ≥≥，即231325k -+≥=---且123134k +≤=+，所以1354k -≤≤．故选：B ．13．（2023北京）已知坐标平面内三点()()()1,1,1,1,1A B C -，D 为ABC 的边AC 上一动点，则直线BD 斜率k 的变化范围是（）A ．3⎡⎢⎣⎦B ．(],0⎫-∞⋃+∞⎪⎣⎭C ．⎣D ．(]),0-∞⋃+∞【答案】D【解析】如图所示，11110,1121AB BC k k -+-===+-因为D 为ABC 的边AC 上一动点，所以直线BD 斜率k 的变化范围是(]),0-∞⋃+∞.故选：D.14．（2023春·上海杨浦）已知常数R a ∈，直线1l ：20x ay +-=，2l ：10ax y ++=，则1a =是12//l l 的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A【解析】因为直线1l ：20x ay +-=，2l ：10ax y ++=，当12//l l 时211112a a ⎧⨯=⎨⨯≠-⎩，解得1a =±，所以1a =是12//l l 的充分不必要条件.故选：A15．（2023·四川南充）已知倾斜角为α的直线l 与直线20x y λ+-=垂直，则tan(π)α-+=（）A ．12B ．2C ．12-D ．2-【答案】B【解析】设直线l 的斜率为1k ，直线20x y λ+-=的斜率为2k ，由直线20x y λ+-=得出斜率212k =-，因为直线l 与直线20x y λ+-=垂直，所以121k k ×=-，即1112k -=-，解得12k =，即tan 2α=，所以()tan πtan 2αα-+==，故选：B ．16．（2023北京）若直线l 与x 轴交于点A ，其倾斜角为α，直线l 绕点A 顺时针旋转45°后得直线1l ，则直线1l 的倾斜角可能为（）A ．45α+︒B ．135α+︒C ．45α-︒D ．135α︒-【答案】BC【解析】当45α≥︒时，直线1l 的倾斜角为45α-︒（如直线AC 旋转至直线AD ）；当045α︒≤<︒时，直线1l 的倾斜角为180(45)135αα︒-︒-=︒+（如直线AD 旋转至直线AB ）.故选：BC.17．（2022秋·福建宁德·高二统考期中）（多选）已知直线l 的倾斜角等于30︒，且l 经过点(0,1)，则下列结论中正确的是（）A ．l 的一个方向向量为n =B ．l 的一个法向量为m =C．l 320y -+=平行D ．l 20y ++=垂直【答案】ACD【解析】直线l 的倾斜角等于30︒，则直线l 的斜率为tan 30︒=对于A ，因为直线l 的斜率为3，则l 的一个方向向量为n =，A 正确；对于B ，0m n ⋅=≠，法向量m =与直线l 不垂直，B 错；对于C 320y -+=的斜率为3，且不过(0,1)，C 正确；对于D 20y ++=的斜率为，则斜率之积为1-，故两直线垂直，D 正确.故选：ACD18．（2022秋·高二课时练习）（多选）下列说法中，正确的有（）A ．斜率均不存在的两条直线可能重合B ．若直线12l l ⊥，则这两条直线的斜率的乘积为1-C ．若两条直线的斜率的乘积为1-，则这两条直线垂直D ．两条直线12,l l ，若一条直线的斜率不存在，另一条直线的斜率为零，则12l l ⊥【答案】ACD【解析】对于A ，若12:0:2,0l l x x ==，则12,l l 斜率均不存在，但两者重合，故A 正确；对于BD ，若一条直线的斜率不存在，另一条直线的斜率为零，则这两条直线互相垂直，但此时乘积不为1-，故B 错误；D 正确；对于C ，根据直线垂直的性质可知，两直线的斜率存在，且乘积为1-时，这两条直线垂直，故C 正确.故选：ACD.19．（2023·江苏·高二假期作业）直线2(2)10a a x y +-+=（a 为常数）的倾斜角的取值范围是．【答案】π3π0,,π24⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭【解析】因为直线2(2)10a a x y +-+=（a 为常数）的斜率为222(1)11a a a +=+-≥-，所以直线的倾斜角θ满足tan 1θ≥-，因为[0,π)θ∈，所以π0,2θ⎡⎫∈⎪⎢⎣⎭或3π,π4θ⎡⎫∈⎪⎢⎣⎭，即直线的倾斜角的取值范围是π3π0,π24⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭ .故答案为：π3π0,π24⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭20．（2023·江苏）过不重合的222(2,3),(3,2)A m m B m m m +---两点的直线l 的倾斜角为45︒，则m 的取值为．【答案】2-【解析】由题意知tan451A B k =︒=，所以2223212(3)m m m m m --=+---，即22232123m mm m m --=+-++，化简得2320m m ++=，解得1m =-或2m =-当1m =-时，(3,2),(3,2)A B --重合，不符合题意舍去，当2m =-时，(6,1),(1,4)A B -，符合题意，所以2m =-，故答案为：2-21．（2023秋·高二课时练习）直线l 的斜率为k ，且k ⎛∈ ⎝⎭，则直线l 的倾斜角的取值范围是．【答案】π2π0,,π63⎡⎫⎛⎫⎪ ⎪⎢⎣⎭⎝⎭【解析】如图：当直线l的斜率3k ⎛⎫∈ ⎪ ⎪⎝⎭，直线l 的倾斜角的取值范围为：π2π0,π63⎡⎫⎛⎫⎪ ⎪⎢⎣⎭⎝⎭ .故答案为：π2π0,π63⎡⎫⎛⎫⎪ ⎪⎢⎣⎭⎝⎭.22．（2023春·上海宝山）在平面直角坐标系xOy 中，锐角θ的大小如图所示，则tan θ=.【答案】23【解析】由()0,0O ，()1,5P ，则直线OP 的方程为5y x =，设其倾斜角为α，即π4αθ=+，由tan 5α=，则πtan 54θ⎛⎫+= ⎪⎝⎭，即πtan tan45π1tan tan 4θθ+=-，解得2tan 3θ=.故答案为：23.23．（2023春·上海松江·高二上海市松江二中校考期中）已知点()0,8A -，()2,2B -，()4,C m ，若线段AB ，AC ，BC 不能构成三角形，则m 的值是.【答案】4【解析】因为线段AB ，AC ，BC 不能构成三角形，所以,,A B C 三点共线，显然直线AB 的斜率存在，故AB AC k k =，即288204m -++=-，解得4m =，故答案为：424（2022·全国·高一假期作业）已知四边形MNPQ 的顶点()()()()1,1,3,1,4,0,2,2M N P Q -，则四边形MNPQ 的形状为.【答案】矩形【解析】()11201,11324MN PQ k k ---==-==--- ，且P 不在直线MN 上，//MN PQ ∴.又()01211,12143MQ NP k k ---====-- ，且N 不在直线上，//MQ NP ∴，∴四边形MNPQ 为平行四边形.又1,MN MQ k k MN MQ ⋅=-∴⊥ .∴平行四边形MNPQ 为矩形.故答案为：矩形.1．（2022秋·黑龙江大庆·高二大庆实验中学校考期末）设直线l 的方程为66cos 130x y β-+=，则直线l 的倾斜角α的范围是（）A ．[0,]πB ．ππ,42⎡⎤⎢⎥⎣⎦C ．π3π,44⎡⎤⎢⎣⎦D ．πππ3,,422π4⎡⎫⎛⎤⋃⎪ ⎢⎣⎭⎝⎦【答案】C【解析】当cos 0β=时，方程变为6130+=x ，其倾斜角为π2，当cos 0β≠时，由直线方程可得斜率1tan cos αβ==k ，[]cos 1,1β∈- 且cos 0β≠，][(),11,k ∴∈-∞-⋃+∞，即][()tan ,11,α∈-∞-⋃+∞，又[)0,πα∈，πππ3π,,4224α⎡⎫⎛⎤∴∈⋃⎪ ⎢⎥⎣⎭⎝⎦，由上知，倾斜角的范围是π3π,44⎡⎤⎢⎥⎣⎦．故选：C ．2．（2023·江西南昌·校联考模拟预测）已知直线l 与直线210x y ++=垂直，若直线l 的倾斜角为θ，则3πsin sin 2θθ⎛⎫+= ⎪⎝⎭（）A ．35B ．12C ．12-D ．25-【答案】D【解析】因为直线l 与直线210x y ++=垂直，所以直线l 的斜率为2，所以tan 2θ=，所以()2223πsin cos tan 2sin sin sin cos 2sin cos tan 15θθθθθθθθθθ⎛⎫+=⋅-=-=-=- ⎪++⎝⎭.故选：D.3．（2022秋·福建宁德·高二福建省宁德第一中学校考阶段练习）（多选）已知直线()212:340,:250l ax y l x a y a ++=+-+-=，则（）A ．若1a =，则1l 的一个方向向量为()3,1-B ．若12l l ∥，则1a =-或3a =C ．若12l l ⊥，则32a =D ．若1l 不经过第二象限，则0a ≤【答案】ACD 【解析】对A ，当1a =时，1340:l x y ++=，斜率为13-，则其一个方向向量为()3,1-，故A 正确；对B ，若12l l ∥，当2a =时，显然不合题意，则2a ≠，则直线1l 的斜率13a k =-，直线2l 的斜率212k a -=-，则有12k k =，即132a a =-，解得3a =或1-，当1a =-时，此时直线12340,:340:l x y l x y -++=--=，显然两条直线重合，故B 错误；对C ，若12l l ⊥，当2a =时，显然不合题意，则2a ≠，则121k k ×=-，即1132a a ⋅=--，解得32a =，故C 正确；对D ，若1l 不经过第二象限，1:340l ax y ++=，化简得433a y x =--，则03a -≥，解得0a ≤，故D 正确；故选：ACD.4．（2023·全国·模拟预测）已知点()2cos10,2sin10P ，()2cos130,2sin130Q ，则直线PQ 的倾斜角为．【答案】160o【解析】方法一：设直线PQ 的倾斜角为()0180θθ≤< ，则()()3sin10sin 12010sin102sin1302sin1022tan 2cos1302cos10cos 12010cos10θ-+--===-+-3sin101030sin 20sin 202tan 20sin 70cos 20-=-=-=- tan160= .∴直线PQ 的倾斜角为160o ；方法二：由三角函数的定义可知：点,P Q 在圆224x y +=上，如图所示，设M 为直线PQ 与x 轴的交点，则10POM ∠= ，130QOM ∠= ，120POQ ∴∠= ，又OP OQ =，30OQM ∴∠= ，160QMx QOM OQM ∴∠=∠+∠= ，∴直线PQ 的倾斜角为160o .故答案为：160o .5．（2023·湖南衡阳·校考模拟预测）点()11,M x y 在函数e x y =的图象上，当[)10,1x ∈，则1111y x +-的取值范围为.【答案】(],2-∞-【解析】由1111y x +-表示()11,M x y 与点()1,1A -所成直线的斜率k ，又由()11,M x y 是e x y =在[)0,1x ∈部分图象上的动点，如图所示：可得(0,1),(1,e)C B ，则2AC k =-，所以2k ≤-，即k 的取值范围为(],2-∞-.故答案为：(],2-∞-.6．（2023云南）设两直线()220m x y m +--+=，0x y +=与x 轴构成三角形，则m 的取值范围为.【答案】{|2m m ≠±且}3m ≠-【解析】当直线()220m x y m +--+=，0x y +=及x 轴两两不平行，且不共点时，必围成三角形当3m =-时，直线()220m x y m +--+=与直线0x y +=平行；当2m =-时，直线()220m x y m +--+=与x 轴平行；当2m =时，直线()220m x y m +--+=，0x y +=及x 轴都过原点；要使得两直线()220m x y m +--+=，0x y +=与x 轴构成三角形，则m 的取值范围为{|2m m ≠±且}3m ≠-故答案为：{|2m m ≠±且}3m ≠-7．（2023秋·高二课时练习）已知直线222111a y x a a =+++与x 轴交于点A 点，与y 轴交于点B ．(1)若π6OAB ∠=，求a 的值；(2)求直线l 的倾斜角的取值范围．【答案】(1)a =a =(2)π3π0,,π44⎛⎤⎡⎫ ⎪⎥⎢⎝⎦⎣⎭【解析】（1）根据题意，直线222111a y x a a =+++，其斜率221a k a =+，在y 轴上的截距为211a +，若a<0，则0k <，π6OAB ∠=，则直线的倾斜角为π5ππ-66=，则有25π2tan 613a a ==-+，变形可得210a ++=，解可得：a =若0a >，则0k >，π6OAB ∠=，则直线的倾斜角为π6，则有2π2tan 613a a ==+，变形可得210a -+=，解可得：a =综上：a =a =（2）根据题意，直线的斜率221a k a =+，设直线的倾斜角为θ.当0a =时，0k =，直线的倾斜角为0，此时直线222111a y x a a =+++与x 轴没有交点，不符合题意；当0a >时，22211a k a a a==++，又由12a a +≥=，当且仅当1a =时等号成立，必有212k ≤=，则有tan 1θ≤，则π04θ<≤；当a<0时，22211a k a a a==-+-+-，又由12a a -+≥=-，当且仅当1a =-时等号成立，必有212k ≥-=-，则有tan 1θ≥-，则3ππ4θ≤<；综上所述：故θ的取值范围为π3π0,π44⎛⎤⎡⎫ ⎪⎥⎢⎝⎦⎣⎭.8．（2023北京）已知()1,2A ，()5,0B ，()3,4C .（1）若A ，B ，C ，D 可以构成平行四边形，求点D 的坐标；（2）在（1）的条件下，判断A ，B ，C ，D 构成的平行四边形是否为菱形.【答案】（1）（-1，6）或（7，2）或（3，-2）；（2）平行四边形ABCD 为菱形,平行四边形ABDC ,ACBD 不是菱形.【解析】（1）由题意得021512AB k -==--，42131AC k -==-，40235BC k -==--，设(),D a b .若四边形ABCD 是平行四边形，则CD AB k k =，AD BC k k =，即4132221b a b a -⎧=-⎪⎪-⎨-⎪=-⎪-⎩，解得16a b =-⎧⎨=⎩，即()1,6D -.若四边形ABDC 是平行四边形，则CD AB k k =，BD AC k k =，即4122015b a b a -⎧=-⎪⎪-⎨-⎪=⎪-⎩，解得72a b =⎧⎨=⎩，即()7,2D .若四边形ACBD 是平行四边形，则CD AB k k =，BD AC k k =，即015221b a b a -⎧=⎪⎪-⎨-⎪=-⎪-⎩，解得32a b =⎧⎨=-⎩，即()3,2D -.综上，点D 的坐标为（-1，6）或（7，2）或（3，-2）.（2）若D 的坐标为（-1，6），因为1AC k =，60115BD k -==---，所以1AC BD k k =-⋅，所以AC BD ⊥，所以平行四边形ABCD 为菱形.若D 的坐标为（7，2），因为2BC k =-，22071AD k -==-，所以01BC AD k k ⋅=≠-，所以平行四边形ABDC 不是菱形.若D 的坐标为（3，-2），因为12AB k =-，直线CD 的斜率不存在，所以平行四边形ACBD 不是菱形.因此，平行四边形ABCD 为菱形,平行四边形ABDC ,ACBD 不是菱形.。