微波技术基础课后习题(A)

微波技术基础课后习题答案1 第二章2.9 22.8a mm =，10.15b mm =，工作波长12mm λ=。

10TE 模：245.6c a mm λλ==>，可以存在；01TE 模：220.3c b mm λλ==>，可以存在；02TE模：10.15c b mm λλ===<，不可以存在；11TE (11TM )模：18.5454c mm λλ===≈>,可以存在；12TE (12TM )：9.9075c mm λλ===≈<， 不存在；21TE (21TM )模：15.1641c mm λλ===≈>， 可以存在；20TE模：22.8c a mm λλ===>，可以存在；30TE模：215.23c a mm λλ===>，可以存在； 40TE模：111.42c a mm λλ===<，不可以存在； 31TE （31TM ）：12.167c mm λλ===≈>，可以存在。

2.11 根据空气填充矩形波导的几何尺寸，22.86a mm =，10.16b mm =。

10TE 模：245.6c a mm λ==；01TE 模：220.3c b mm λ==；20TE模：22.86c a mm λ===；11TE (11TM )模：18.5454c mm λ===≈； 因此在所有工作模式中，工作频率低于20TE 模截止频率且高于10TE 模截止频率的传输频率才能实现单模传输。

其对应的频率范围是1083310 6.5645.7210TE m s f GHz m -⨯==⨯，208331013.1222.8610TE m s f GHz m-⨯==⨯。

因此该矩形波导单模传输的频率范围是6.5613.12GHz f GHz <<。

2.15 圆波导的主模为11TE 模，其截止波长3.41 3.41310.23c R cm cm λ==⨯=； 截止频率892310 2.931010.2310c f Hz -⨯==⨯⨯；波导波长2247.426w cm λ--====≈；波形阻抗111787TE Z ===Ω. 2.20 对于传输01TE 模式的圆波导，磁场只有r H 和z H 分量，并且在波导管壁内表面只有z H 磁场分量。

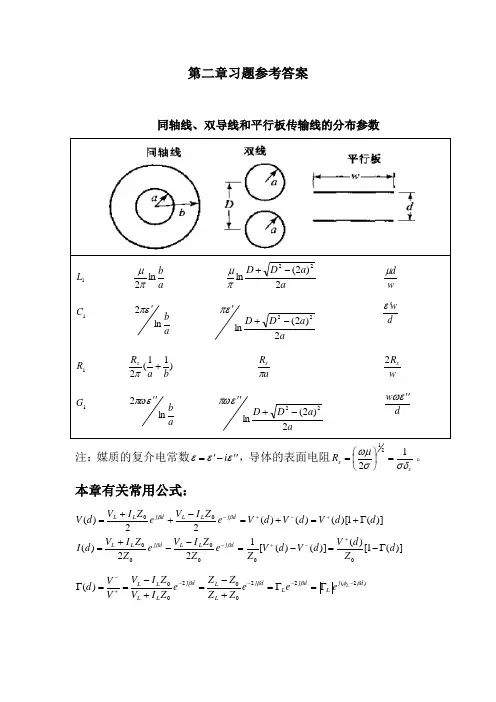
第二章习题参考答案同轴线、双导线和平行板传输线的分布参数注：媒质的复介电常数εεε''-'=i ，导体的表面电阻ss R σδσωμ1221=⎪⎭⎫⎝⎛=。

本章有关常用公式：)](1[)()]()([122)()](1)[()()(22)(00000000d Z d V d V d V Z e Z Z I V e Z Z I V d I d d V d V d V e Z I V e Z I V d V d j L L d j L L dj L L d j L L Γ-=-=--+=Γ+=+=-++=+-+-+-+-ββββ )2(2200200)(d j L d j L dj L L d j L L L L L e e e Z Z Z Z e Z I V Z I V VV d βφβββ----+-Γ=Γ=+-=+-==ΓL Lj L j L L L L L e e Z Z Z Z Z Z Z Z φφΓ=+-=+-=Γ0000dtg jZ Z dtg jZ Z Z d Z L L in ββ++=000)()(1)(1)()()(0d d Z d I d V d Z in Γ-Γ+==LL VV VSWR Γ-Γ+==11minmax2.1无耗或者低耗线的特性阻抗为110C L Z = 平行双导线的特性阻抗：aDa a D D a a D D Z r r rln 11202)2(ln 11202)2(ln 112222000εεεμεπ≈-+=-+=已知平行双导线的直径mm a 22=，间距cm D 10=，周围介质为空气（1=r ε），所以特性阻抗)(6.5521100ln 120ln11200Ω==≈a D Z rε 同轴线的特性阻抗：ab a b Z r rln 60ln 121000εεμεπ==已知同轴线外导体的内直径2mm b 23=，内导体的外直径2mm a 10=，中间填充空气(1=r ε)：特性阻抗)(50210223ln 60ln 600Ω===abZ r ε中间填充介质(25.2=r ε)：特性阻抗)(3.33210223ln 25.260ln 600Ω===a b Z r ε2.2对于无耗传输线线有相位常数μεωωβ===k C L 11，所以可求出相速度v k C L v p =====μεωβω1111，等于电磁波的传播速度。

思考题1.1 什么是微波？微波有什么特点？1.2 试举出在日常生活中微波应用的例子。

1.3 微波波段是怎样划分的？1.4 简述微波技术未来的发展状况。

2.1何谓分布参数？何谓均匀无损耗传输线？2.2 传输线长度为10cm，当信号频率为9375MHz时，此传输线属长线还是短线？10cm，当信号频率为150KHz时，此传输线属长线还是短线？2.4传输线特性阻抗的定义是什么？输入阻抗的定义是什么？2.5什么是反射系数、驻波系数和行波系数？2.6传输线有哪几种工作状态？相应的条件是什么？有什么特点？3.1何谓矩形波导？矩形波导传输哪些模式？3.2何谓圆波导？圆波导传输哪些模式？？3.3矩形波导单模传输的条件是什么？3.4何谓带状线？带状线传输哪些模式？3.5何谓微带线？微带线传输哪些模式？何谓截止波长？何谓简并模？工作波长大于或小于截止波长，电磁波的特性有何不同？3.7 矩形波导TE10模的场分布有何特点？3.8何谓同轴线？传输哪些模式？波导具有高通滤波器的特性？3.10 TE波、TM波的特点是什么？3.11何谓波的色散？3.12任何定义波导的波阻抗？分别写出TE波、TM波波阻抗与TEM波波阻抗之间的关系式。

4.1为什么微波网络方法是研究微波电路的重要手段？4.2微波网络与低频网络相比有哪些异同？4.3网络参考面选择的要求有什么？4.4表征微波网络的参量有哪几种？分别说明它们的意义、特性及其相互间的关系？4.5二端口微波网络的主要工作特性参量有哪些？4.6微波网络工作特性参量与网络参量有何关系？4.7常用的微波网络有哪些？对应的网络特性参量是什么？4.8微波网络的信号流图是什么？简要概述信号流图化简法则有哪些？5.1试述旋转式移相器的工作原理，并说明其特点。

5.2试分别叙述矩形波导中的接触式和抗流式接头的特点。

5.3试从物理概念上定性地说明：阶梯式阻抗变换器为何能使传输线得到较好的匹配。

5.4在矩形波导中，两个带有抗流槽的法兰盘是否可以对接使用?5.5微波元件中的不连续性的作用和影响是什么?5.6利用矩形波导可以构成什么性质的滤波器?5.7试说明空腔谐振器具有多谐性，采用哪些措施可以使腔体工作于一种模式?5.8欲用空腔谐振器测介质材料的相对介电常数，试简述其基本原理和方法。

《微波技术基础》题集一、选择题（每题2分，共20分）1.微波是指频率为（）的电磁波。

A. 300MHz-300GHzB. 300Hz-300MHzC. 300GHz-300THzD. 300kHz-300MHz2.微波在真空中的传播速度与（）相同。

A. 光速B. 声速C. 电场传播速度D. 磁场传播速度3.微波的主要特性不包括（）。

A. 直线传播B. 穿透性强C. 反射性D. 绕射能力强4.微波传输线主要包括（）。

A. 同轴电缆和光纤B. 双绞线和同轴电缆C. 光纤和波导D. 双绞线和波导5.在微波通信中，常用的天线类型是（）。

A. 偶极子天线B. 抛物面天线C. 环形天线D. 螺旋天线6.微波谐振腔的主要作用是（）。

A. 储存微波能量B. 放大微波信号C. 转换微波频率D. 衰减微波信号7.微波加热的原理是（）。

A. 微波与物体内部的分子振动相互作用B. 微波使物体表面温度升高C. 微波直接转化为热能D. 微波引起物体内部化学反应8.微波在介质中的传播速度与介质的（）有关。

A. 密度B. 介电常数C. 磁导率D. 温度9.微波通信中，为了减少信号的衰减，通常采取的措施是（）。

A. 增加信号频率B. 减小信号功率C. 使用中继站D. 改用光纤通信10.微波测量中，常用的仪器是（）。

A. 示波器B. 微波功率计C. 万用表D. 频谱分析仪（部分功能重叠，但更专用于频率分析）二、填空题（每题2分，共20分）1.微波的频率范围是_________至_________。

2.微波在真空中的传播速度约为_________m/s。

3.微波的_________特性使其在雷达和通信系统中得到广泛应用。

4.微波传输线中，_________具有宽频带、低损耗的特点。

5.微波天线的作用是将微波能量转换为_________或相反。

6.微波加热过程中，物体吸收微波能并将其转化为_________。

7.微波在介质中的衰减主要取决于介质的_________和频率。

第四章习题参考答案带状线为双导体结构，中间填充均匀介质，所以能传输TEM 导波，且为带状线的工作模式。

4.1可由P.107:4.1-7式计算特性阻抗0Z 由介质r ε，导体带厚度与接地板高度的比bt ，以及导体带宽度与接地板高度的比bW确定。

Ω=45.690Z4.5可由P.107:4.1-6式计算⎪⎩⎪⎨⎧>--<=1206.085.012000Z x Z x b W r r εε 其中： 441.0300-=Z x r επ已知：1202.74502.20<=⨯=Z r ε 83.0441.02.7430441.0300=-=-=πεπZ x r 所以： )(66.283.02.3mm bx W =⨯==衰减常数P.109:4.1-10：d c ααα+=c α是中心导体带和接地板导体的衰减常数，d α为介质的衰减常数。

TEM 导波的介质损耗为：)/(2m Np ktg d δα=，其中εμω'=k 由惠勒增量电感法求得的导体衰减常数为)/(m Np ：P.111:4.1-11⎪⎪⎩⎪⎪⎨⎧Ω>Ω<-⨯=-12016.0120)(30107.200003Z B b Z R Z A t b Z R r s r r s c εεπεα 其中：⎪⎭⎫⎝⎛--++-+=t t b t b t b t b W A 2ln 121π ⎪⎭⎫⎝⎛++-++++=t W W t t b t b t W b B πππ4ln 21414.05.01)7.05.0(1)/(155.02001.0100.32.21010222289m Np tg c f ktg r d =⨯⨯===πδεπδα 铜的表面电阻在10GHz 下Ω==026.02σωμs R ，74.4=A m Np A t b Z R r s c /122.0)(30107.203=-⨯=-πεαm Np d c /277.0=+=αααdB e Np 686.8lg 1012==m dB m Np d c /41.2/277.0==+=ααα4.6可由P.107:4.1-6式计算⎪⎩⎪⎨⎧>--<=1206.085.012000Z x Z x b W r r εε 其中: 441.0300-=Z x r επ已知：1204.1481002.20>=⨯=Z r ε 194.0441.04.14830441.0300=-=-=πεπZ x r 所以： )(67.02128.016.3)6.085.0(mm x b W =⨯=--= 在10GHz ，带状线的波长为：cm fcr 02.210102.210398=⨯⨯⨯==ελ4.16可由P.130:4.3-27式计算已知Ω=700e Z ，Ω=300o Z ，mm b 4=，1.2=r ε3813.3300==re e Z A ε648.02212212143813.33813.3214=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛+--=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+--=e e e e k e eA A e45.1300==ro o Z A ε99.022222=⎪⎪⎪⎭⎫⎝⎛+-=o o A A o e e k ππ68.02==o e k k arctg b W π015.0112=⎪⎪⎭⎫⎝⎛--=oee o k k k k arctg b S π mm b 4=mm W 7.268.04=⨯= mm S 06.0015.04=⨯=廖承恩第6章习题6－5 求图6－1 所示的对称二端口网络的归一化ABCD 矩阵，并求不引起附加反射的条件。

微波技术基础第四章课后答案___杨雪霞汇总4-1 谐振腔有哪些主要的参量？这些参量与低频集总参数谐振回路有何异同点？答：谐振腔的主要特性参数有谐振频率、品质因数以及与谐振腔中有功损耗有关的谐振电导，对于一个谐振腔来说，这些参数是对于某一个谐振模式而言的，若模式不同，这些参数也是不同的。

谐振频率具有多谐性，与低频中的回路，当其尺寸、填充介质均不变化时，只有一个谐振频率是不相同的。

在谐振回路中，微波谐振腔的固有品质因数要比集总参数的低频谐振回路高的多。

一般谐振腔可以等效为集总参数谐振回路的形式。

4-2 何谓固有品质因数、有载品质因数？它们之间有何关系？答：固有品质因数是对一个孤立的谐振腔而言的，或者说，是谐振腔不与任何外电路相连接（空载）时的品质因数。

当谐振腔处于稳定的谐振状态时，固有品质因数0Q 的定义为02TWQ W π=，其中W 是谐振腔内总的储存能量，T W 是一周期内谐振腔内损耗的能量。

有载品质因数是指由于一个腔体总是要通过孔、环或探针等耦合机构与外界发生能量的耦合，这样不仅使腔的固有谐振频率发生了变化，而且还额外地增加了腔的功率损耗，从而导致品质因数下降，这种考虑了外界负载作用情况下的腔体的品质因数称为有载品质因数l Q 。

对于一个腔体，01l Q Q k=+，其中k 为腔体和外界负载之间的耦合系数。

4-4 考虑下图所示的有载RLC 谐振电路。

计算其谐振频率、无载Q 0和有载Q L 。

谐振器负载1800Ω解：此谐振电路属于并联谐振电路，其谐振频率为：0356f MHz ===无载时，017.9R Q w L====有载时，040.25L e R Q w L ====根据有载和无载的关系式111L e Q Q Q=+得： 1112.5111140.2517.9L e Q Q Q===++4-5 有一空气填充的矩形谐振腔。

假定x 、y 、z 方向上的边长分别为a 、b 、l 。

试求下列情形的振荡主模及谐振频率：（1）a b l >>；（2）a l b >>；（3）l a b >>；（4）a b l ==。

第六章习题参考答案6.5: 已知并联导纳的ABCD 矩阵⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡101Y D C B A 和一段传输线的ABCD 矩阵l ch V l V V V A L I L I γ=====021)(2 l Z s h I l V I V B L V L V γ=====021)(2Z lsh V l I V I C L I LI γ=====021)(2 l ch I l I I I D L V LV γ=====021)(2对于无耗线:l j l ch A ββγγcos )(=== l jZ j l Zsh B ββγγsin )(=== l Zj j Z l sh C ββγγsin 1)(===l j l ch D ββγγcos )(=== 总的ABCD 矩阵为三个二端口网络ABCD 矩阵的乘积⎥⎥⎦⎤⎢⎢⎣⎡--+-=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡θθθθθθθθθθθsin cos sin 1cos 2sin sin cos 101cos sin 1sin cos 10122BZ i Z Z B jB jZ BZ jB Zj jZ jB D C B A 则总的归一化ABCD 矩阵为：⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡D CZ Z BAd c b a 00 由S 矩阵ABCD 矩阵的关系式⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+----++++=D CZ B Z A BC AD D CZ B Z A D CZ B Z A S 00000012)(2111][ 可求出S 矩阵。

对于本题目求出不引起附加反射的条件，只需求θθcos 2sin )1(00220011B Z Z B Z Z Z Z S =⎥⎦⎤⎢⎣⎡--⇒=由上式可得各参数满足的关系式02)1(20202202=--+Z tg BZ Z Z tg Z B θθ6.9由题意知(a)和(c)图均为右端或中断开路的一端口网络，求S 矩阵只需求始端反射系数即可（略）(b)图为并联导纳的S 矩阵（参考6.5）（略） 6.14 推导：原来第i 个参考面位于0=i z ，归一化入射和反射波为：i i b a , 当第i 个参考面移到i i l z =时，归一化入射和反射波为：i i j i i j i i e b b e a a θθ='='-,，其中giii l λπθ2=（p.21，2.1-14）j i j i j j ij j j ji j i ije S e a b a b S θθθθ----==''=' 写成矩阵形式为：]][][[][P S P S ='其中： ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=---N j j j e e e P θθθ0000][21已知：参考面21,T T 处的S 矩阵⎥⎦⎤⎢⎣⎡=22211211S S S S S⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=--221121220000][g g l j l j j j e e e e P λπλπθθ 则由公式]][][[][P S P S ='可求出][S '。

1、1_3_4_11_13_15_16_17解题1．1、解：()()()()()()()()()z t t Z A t z i z t t z v tt A t v z t A t z v cL βωφωβωωφωφβω+=+=+=∴=+=++=cos 1.0cos ,cos 10,cos 10cos ,0cos ,111111所以，t t i t t t v T t t i t t t v T t t i t t t v T ωλωπωλωλωπωλπωλπωπωλcos 1.0,2cos 1022cos 10,2:sin 1.0,4sin 1042cos 10,4:4cos 1.0,84cos 1082cos 10,8:321-=⎪⎭⎫⎝⎛-=⎪⎭⎫⎝⎛+=⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛1．3、解：z j zj zj z Z j z j Z Z L L in βββββcot tan 1tan tan 1tan -=∞++∞=++=1）300=f MHz ，1==fcλ m ，02cot 25.12cot cot =-=-=-=πλλπβj j z j Z in 2）600=f MHz ，5.0==fcλ m ，z ＝2.5λ，∞+=-=-=-=j j j z j Z in πλλπβcot 5.22cot cot 00.25λ0.5λ0.75λ1λ1.25λ0 0z|V|, |I|Z in|V||I|Z in0.5λ1λ1.5λ2λ2.5λz|V|, |I| Z in|V||I|Z in1) 300MHz 时 2) 600MHz 时Fig.1 相应电压、电流、阻抗分布图评论学生作业：头脑中闪现阻抗圆图1．4、解：（用阻抗圆图来做更快） a ）()Ω===Γ=+-=Γ1000'c inaa cL cL L Z Z z Z Z Z Z b ）（I ）段：开路()()042cotcot 1'22=-=-==Γ=Γ=+-=Γ--πβββc c bb zj z j L cL cL L jZ z jZ I Z e e z Z Z Z Z ；（II ）段：短路()()∞===-=Γ=Γ-=+-=Γ--j jZ z jZ II Z e e z Z Z Z Z c c bb z j z j L cL cL L 42tantan 1'22πβββ()()()0111''''==+=∴I Z II Z I Z Z bb bb bb bb 总阻抗 评论：学生()()zj in in e z j z zzj z zz j z j zj zj z j Z Z z I ββββββββββββ222222sin 2cos tan 1tan 2tan 1tan 1tan 11tan tan 11tan 11tan 111)(-=-=+--=+-=+-=+-=+-=Γ结束了 （III ）段：短路()∞===-=Γ=Γ-=+-=+-=Γ--j jZ z jZ Z e e z Z Z Z Z Z Z Z Z c c inaa zj z j L cbb cbb c L c L L 42tantan 1'22''πβββc)（I ）段，短路，()()∞=-=Γ-j I Z e z bb zj '2β； （II ）段，匹配，()()c bb Z II Z z ==Γ'0()()()c bb bb bb bb Z II Z II Z I Z Z ==+=∴''''111总阻抗（III ）段：匹配()Ω===Γ 2000'c inaa Z Z zd )（I ）段：开路()()∞+=-=-==Γ-j jZ z jZ I Z e z c c bb zj 22cot cot '2πββ；（II ）段：()()()Ω===++=++==Γ=Γ=+-=+-=Γ-- 30022tan 21tan 2tan 1tan 3131150300150300''22c bb L L bb zj z j L c L c L L Z II Z j j z Z j z j Z II Z e e z Z Z Z Z ππββββ ()Ω==∴ 300''II Z Z bb bb 总阻抗（III ）段：()Ω===++=++==Γ=Γ=+-=+-=Γ-- 7521212tan 212tan2tan 1tan 3131150300150300''''22c inaa bb bb inaa zj z j L c L c L L Z Z j j z Z j z j Z Z e e z Z Z Z Z ππββββ1．11、证明：minmin minmin minmin minmin min tan 1tan i.e.tan 1tan tan tan tan 1tan z jK z j K Z Z z jK z j K Z z j Z z K Z j K z Z j z j Z K Z cL L L L L L ββββββββ--=--=+=+++==1．13、证明： 评论学生作业：22?c L c L Z Z Z Z =⇒=方法1：θj L cL e Z Z Z =∴=可令则()()()[]()[]()()θθθθθθθθθθθθθθθλλπλλπββθθsin 1cos cos sin 1cos 2cos sin 1cos sin 1sin 1cos cos sin 1sin 1cos 182tan 182tantan 1tan 2222-=+-=+---++=+-++=++=++=++=j j j j jej e Z j j Z l Z j l j Z Z j j LL L L in方法2：2tan cos 1sin 111111θθθθθj j e e Z Z Z j j L L L LL L =+=+-=+-=ΓΓ-Γ+=原点的虚轴上！而不仅仅在落在Γ==⇒=L L L cL Z Z Z Z Z 11?为纯虚数，L Z 落在阻抗圆图的虚轴上，向源旋转⎪⎭⎫⎝⎛28πλ即，输入阻抗落在圆图实轴上，即0=X ，为纯电阻。

5-2若一两端口微波网络互易，则网络参量[]Z 、[]S 的特征分别是什么？ 解： 1221Z Z = 1221S S =5-4 某微波网络如右图。

写出此网络的[ABCD]矩阵，并用[ABCD]矩阵推导出对应的[S]及[T]参数矩阵。

根据[S]或[T]阵的特性对此网络的对称性做出判断。

75Z j =Ω解： 因为，312150275,2125025j j A A A jj --⎡⎤⎡⎤⎢⎥⎢⎥===⎢⎥⎢⎥-⎣⎦⎣⎦所以，12313754212004j A B A A A jC D ⎡⎤--⎢⎥⎡⎤==⎢⎥⎢⎥⎣⎦⎢⎥--⎢⎥⎣⎦因为，归一化电压和电流为：()()()i i i V z a z b z ==+()(()()i i i i I z I z a z b z ==-(1)归一化ABCD 矩阵为： 00/AB Z a b CZ D c d ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦(2)所以： 1122220()()/a b A a b B a b Z +=++-1102222()()a b CZ a b D a b -=++-(3)从而解得：1001100221(/)1(/)1()1()A B Z A B Z b a CZ D CZ D b a ----+⎡⎤⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎢⎥----+⎣⎦⎣⎦⎣⎦⎣⎦(4)所以进而推得[S]矩阵为：⎥⎦⎤⎢⎣⎡+-+----++++=D CZ Z B A BC AD D CZ Z B A D CZ Z B A S 000000/2)(2//1][ (5) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--+-=j jj S 2722274211][ (6)由(3)式解得⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-+-++++----+=⎥⎦⎤⎢⎣⎡220000000011////21b a D CZ Z B A D CZ Z B A D CZ Z B A D CZ Z B A a b (7)所以， ⎥⎦⎤⎢⎣⎡-+-++++----+=D CZ Z B A DCZ Z B A D CZ Z B A DCZ Z B A T 00000000////21][(8)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--+--=j j j j T 274214212721][ （9）因为[S]阵的转置矩阵][][S S t=，所以，该网络是互易的。

【关键字】情况、方法、条件、模式、有效、和谐、加大、规律、稳泄、理想、方式、作用、结构、关系、简化、保证、取决于、方向、提髙、中心4-1谐振腔有哪些主要的参疑？这些参量与低频集总参数谐振回路有何异同点？答:谐振腔的主要特性参数有谐振频率、品质因数以及与谐振腔中有功损耗有关的谐振电导, 对于一个谐振腔来说，这些参数是对于某一个谐振模式而言的，若模式不同，这些参数也是不同的。

谐振频率具有多谐性，与低频中的回路，当其尺寸、填充介质均不变化时，只有一个谐振频率是不相同的。

任谐振回路中，微波谐振腔的固有品质因数要比集总参数的低频谐振回路髙的多。

一般谐振腔可以等效为集总参数谐振回路的形式。

4-2何谓固有品质因数、有载品质因数？它们之间有何关系？答：固有品质因数是对一个孤立的谐振腔而言的，或者说，是谐振腔不与任何外电路相连接 (空载)时的品质因数。

当谐振腔处于稳泄的谐振状态时，固有品质因数Qo的左义为WQo=27r——,其中W是谐振腔内总的储存能量，略是一周期内谐振腔内损耗的能量。

W T有载品质因数是指由于一个腔体总是要通过孔、环或探针等耦合机构与外界发生能量的耦合，这样不仅使腔的固有谐振频率发生了变化，而且还额外地增加了腔的功率损耗，从而导致品质因数下降，这种考虑了外界负载作用情况下的腔体的品质因数称为有载品质因数Q O 对于一个腔体，英中k为腔体和外界负载之间的耦合系数。

1 + R4-4考虑下图所示的有载RLC谐振电路。

计算其谐振频率、无载0。

和有载0“解：此谐振电路属于并联谐振电路，苴谐振频率为：无载时，Q = — =竿==/ *°°= 17.9说[L7 720X10~9/10X10_,2有载时，Qe=d = = --------- ---- ---------- = 40.25叫上/Z7 ^OxlO-'/lOxlO-12根据有载和无载的关系式—=—+丄得：Q L Q Q4-5有一空气填充的矩形谐振腔。