分数应用题——转化单位一

六年级数学巧用“单位1”(转化与统一)分数应用题解决策略（五）——转化单位，统一单位，量率对应一、填空1、有一批货物，第一天运了这批货物的 $\frac{1}{3}$，第二天运的是第一天的 $\frac{2}{5}$。

第二天运的是这批货物的 $\frac{8}{15}$。

2、一辆汽车第一天行了全程的 $\frac{3}{5}$，第二天行了余下的 $\frac{2}{5}$，第二天行了全程的。

3、一本书，上午读了 $\frac{1}{4}$，下午读了60页，这时已读页数和未读页数比是1:3.这时已读页数占这本书$\frac{1}{5}$，下午读了60页占这本书的 $\frac{1}{4}$。

4、XXX的质量是梨子的 $\frac{3}{5}$，香蕉质量是苹果的 $\frac{4}{5}$。

香蕉的质量是梨子的 $\frac{12}{25}$。

5、有两筐苹果，甲筐苹果的等于乙筐苹果数的$\frac{3}{4}$。

甲筐苹果数相当于乙筐苹果数的$\frac{4}{3}$。

二、应用1、一条绳子，第一次剪去全长的 $\frac{1}{3}$，第二次剪去余下的 $\frac{2}{3}$，第一次比第二次多剪24米。

求这条绳子的全长。

答：设这条绳子的全长为 $x$ 米，则第一次剪去的长度为$\frac{x}{3}$ 米，第二次剪去的长度为$\frac{2}{3}x-24$ 米。

根据题意得到方程：$\frac{x}{3}=\frac{2}{3}x-24+24$，解得$x=108$，所以这条绳子的全长是108米。

2、六（19）班男生比全班人数的多12人，女生人数占男生人数的 $\frac{3}{4}$，六（19）班共有学生多少人？答：设六（19）班男生人数为 $x$，则女生人数为$\frac{3}{4}x$。

根据题意得到方程：$x+\frac{3}{4}x+12=n$，其中 $n$ 为六（19）班的总人数。

解得 $n=\frac{28}{3}x+12$。

第四讲分数应用题转化单位“ 1、知识梳理分数应用题研究的是数与量的对应关系，确定单位“ 1”是解答分数应用题的关键。

当问题中有多个分率，且这些分率单位“ 1”不同时，要分析不变量，将单位“ 1 ”进行统这种方法叫转化单位“ 1”、方法归纳1. 总量不变，转化为以总量为单位“1”，一种量不变，以不变的量为单位“ 1”，差量不变，以差量为单位“ 1 ”。

2. 在转化的过程中，注意分率与比之间的转化，注意“份数”思想。

三、课堂精讲例1.修路队修一条公路，第一天修了这条公路的-，第二天修了余下的-，已知这两天5 3共修路120米，这条公路全长多少米？【规律方法】总量不变，以总量（这条公路）为单位“。

1【搭配课堂训练题】 【难度分级】A看了 20页，这本书共有多少页?2. 运送一堆水泥，第一天运了这堆水泥的运，这堆水泥有多少吨？例2. （2013天河省实）某校六年级有三个班，在为 4.20雅安地震献爱心的活动中，一班22的捐款数是二、三班捐款数之和的一，二班的捐款数是一、三班捐款数之和的一，已知三35班的捐款数比一班少 180元，问三个班共捐款多少元？ 【规律方法】三个班捐款总量不变，以总量为单位“1 ”。

【搭配课堂训练题】 【难度分级】B13.甲、乙、丙、丁四个筑路队共筑1200米长的一段公路，甲队筑的路是其他三个队的 -211乙队筑的路是其他三个队的 -，丙队筑的路是其他三个队的一 丁队筑了多少米？1. 小方三天看完一本书，第一天看了全书的1，第二天看了余下的:第二天比第一天多1 一 2，第—天运的是第一天的，还剩84吨没有433 4 '4例3 .兄弟两人各有人民币若干元，其中弟的钱数是兄的，若弟给兄4元，则弟的钱数52是兄的3，求兄弟两人原来各有多少元？【规律方法】在变化过程中，不变的是两人总钱数，以总钱数为单位“14. 小明看一本课外读物，读了几天后，已读的页数是剩下页数的-后来他又读了20页81这时已读的页数是剩下页数的-，这本课外读物共有多少页?615. 王师傅生产一批零件，不合格产品是合格产品的，后来从合格产品中又发现了2个不19合格产品，这时算出产品的合格率是94%。

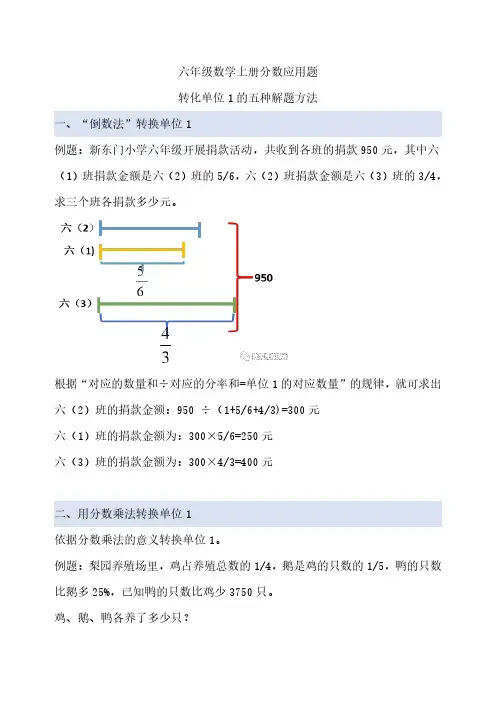
六年级数学上册分数应用题转化单位1的五种解题方法一、“倒数法”转换单位1例题：新东门小学六年级开展捐款活动，共收到各班的捐款950元，其中六（1）班捐款金额是六（2）班的5/6，六（2）班捐款金额是六（3）班的3/4，求三个班各捐款多少元。

根据“对应的数量和÷对应的分率和=单位1的对应数量”的规律，就可求出六（2）班的捐款金额：950÷（1+5/6+4/3)=300元六（1）班的捐款金额为：300×5/6=250元六（3）班的捐款金额为：300×4/3=400元二、用分数乘法转换单位1依据分数乘法的意义转换单位1。

例题：梨园养殖场里，鸡占养殖总数的1/4，鹅是鸡的只数的1/5，鸭的只数比鹅多25%，已知鸭的只数比鸡少3750只。

鸡、鹅、鸭各养了多少只？以养殖总数为单位1，依据分数乘法的意义，鹅占养殖总数的1/4×1/5=1/20，鸭占养殖总数的1/20×(1+25%)=1/16。

鸡、鹅、鸭的分率如下图：这样，鸡与鸭就统一单位1了，都是以养殖总数为单位1的，用鸡与鸭的数量差与分率差相除，就能求出养殖总数了：3750÷（1/4-1/16)=20000只。

鸡的只数：20000×1/4=5000只鹅的只数：20000×1/20=1000只鸭的只数：20000×1/16=1250只三、用份数法转换单位1例题：乌江泥厂有甲、乙、丙、丁四个车间，甲车间人数是其他三个车间的1/4，乙车间人数是其他三个车间的4/11，丙车间人数是其他三个车间的1/2,已知丁车间有60人，该厂有职工多少人？我们可以用全厂职工总数为单位1，用份数法，分别求出甲、乙、丙三车间人数各占全厂职工总数的几分之几，然后，再求出丁车间人数占全厂职工总数的几分之几。

三个车间的分率转换如下：甲车间人数是全厂职工的1÷（1+4）=1/5，乙车间人数占全厂职工的4÷（4+11）=4/15丙车间人数占全厂职工的1÷(1+2)=1/3.现在，本题的数量关系已简化成下图：看图可知，60人的对应分率为1-1/5-4/15-1/3。

转化单位“1”（一）专题简析：把不同的数量当作单位“1”，得到的分率可以在一定的条件下转化。

如果甲是乙的a b ，乙是丙的c d ，则甲是丙的ac bd ；如果甲是乙的a b ，则乙是甲的ba ；如果甲的a b 等于乙的c d ，则甲是乙的c d ÷a b ＝bc ad ，乙是甲的a b ÷a b ＝adbc 。

例题1、乙数是甲数的23 ，丙数是乙数的45 ，丙数是甲数的几分之几？23 ×45 ＝815 练习11、乙数是甲数的34 ，丙数是乙数的35 ，丙数是甲数的几分之几？2、一根管子，第一次截去全长的14 ，第二次截去余下的12 ，两次共截去全长的几分之几？3、一个旅客从甲城坐火车到乙城，火车行了全程的一半时旅客睡着了。

他醒来时，发现剩下的路程是他睡着前所行路程的14 。

想一想，剩下的路程是全程的几分之几？例题2、修一条8000米的水渠，第一周修了全长的14 ，第二周修的相当于第一周的45 ，第二周修了多少米？解一：8000×14 ×45＝1600（米）先求量解二：8000×（14 ×45 ）＝1600（米）先求对应分率 答：第二周修了1600米。

练习2用两种方法解答下面各题： 1、一堆黄沙30吨，第一次用去总数的15 ，第二次用去的是第一次的114倍，第二次用去黄沙多少吨？2、 大象可活80年，马的寿命是大象的12 ，长颈鹿的寿命是马的78 ，长颈鹿可活多少年？3、仓库里有化肥30吨，第一次取出总数的15 ，第二次取出余下的13 ，第二次取出多少吨？例题3、晶晶三天看完一本书，第一天看了全书的14 ，第二天看了余下的25 ，第二天比第一天多看了15页，这本书共有多少页？解： 15÷【（1－14 ）×25 － 14 】＝300（页） 答：这本书有300页。

练习31、有一批货物，第一天运了这批货物的14 ，第二天运的是第一天的35 ，还剩90吨没有运。

转化单位1分数应用题(超经典)————————————————————————————————作者：————————————————————————————————日期：23 “单位1”相关问题复习专题(一)例题1、乙数是甲数的23 ，丙数是乙数的45 ，丙数是甲数的几分之几？23 ×45 ＝815练习11、乙数是甲数的34 ，丙数是乙数的35 ，丙数是甲数的几分之几？2、一根管子，第一次截去全长的14 ，第二次截去余下的12 ，两次共截去全长的几分之几？3、一个旅客从甲城坐火车到乙城，火车行了全程的一半时旅客睡着了。

他醒来时，发现剩下的路程是他睡着前所行路程的14 。

想一想，剩下的路程是全程的几分之几？例题2、修一条8000米的水渠，第一周修了全长的14 ，第二周修的相当于第一周的45，第二周修了多少米？ 解一：8000×14 ×45＝1600（米）先求量解二：8000×（14 ×45 ）＝1600（米）先求对应分率 答：第二周修了1600米。

练习2用两种方法解答下面各题： 1、一堆黄沙30吨，第一次用去总数的15 ，第二次用去的是第一次的114倍，第二次用去黄沙多少吨？2、大象可活80年，马的寿命是大象的12 ，长颈鹿的寿命是马的78，长颈鹿可活多少年？3、仓库里有化肥30吨，第一次取出总数的15 ，第二次取出余下的13 ，第二次取出多少吨？例题3、晶晶三天看完一本书，第一天看了全书的14 ，第二天看了余下的25 ，第二天比第一天多看了15页，这本书共有多少页？解： 15÷【（1－14 ）×25 － 14 】＝300（页） 答：这本书有300页。

练习31、有一批货物，第一天运了这批货物的14 ，第二天运的是第一天的35 ，还剩90吨没有运。

这批货物有多少吨？2、修路队在一条公路上施工。

第一天修了这条公路的14 ，第二天修了余下的23 ，已知这两天共修路1200米，这条公路全长多少米？3、加工一批零件，甲先加工了这批零件的25 ，接着乙加工了余下的49 。

转化单位一的分数应用题
当涉及到将单位转换应用于分数时，这是一个常见的问题类型。

以下是一个转化单位的分数应用题的例子：
问题：小明每分钟可以跑300米。

如果他跑了2/3小时，他一共跑了多少米？
解答：
首先，我们需要将时间从小时转换为分钟，以便与每分钟跑的距离单位匹配。

1小时= 60分钟
由于小明跑了2/3小时，我们可以计算出他跑了多少分钟：
2/3 * 60 = 40分钟
接下来，我们可以计算小明在40分钟内跑了多少米：
每分钟跑300米，所以在40分钟内他跑了：
40 * 300 = 12000米
所以，小明在2/3小时内一共跑了12000米。

这个问题的关键是将不同单位之间的转换应用于分数。

通过正确地转化时间单位并使用分数运算，我们可以解决这类问题。

【奥数讲座】分数应用题转化单位1转化单位1（一）【例题1】乙数是甲数的2/3，丙数是乙数的4/5，丙数是甲数的几分之几？【解答】（8/15）乙数是甲数的2/3，把甲数看作单位1，乙数就是2/3；丙数是乙数的4/5，也就是说丙数是2/3的4/5，“求一个数的几分之几是多少”用乘法，即2/3×4/5＝8/15，丙数是8/15，甲数是1，所以丙数是甲数的8/15。

【练习1】乙数是甲数的3/4，丙数是乙数的6/7，丙数是甲数的几分之几？【解答】（9/14）乙数是甲数的3/4，把甲数看作单位1，乙数就是3/4；丙数是乙数的6/7，也就是说丙数是3/4的6/7，“求一个数的几分之几是多少”用乘法，即3/4×6/7＝9/14，丙数是9/14，甲数是1，所以丙数是甲数的9/14。

【例题2】修一条8000米的水渠，第一周修了全长的1/4，第二周修的相当于第一周的4/5，第二周修了多少米？【解答】（1600米）思考一：第一周修了8000×1/4＝2000米，第二周修了2000×4/5＝1600米。

思考二：第二周占全长的1/4×4/5＝1/5，第二周修了8000×1/5＝1600米。

【练习2】一堆黄沙30吨，第一次用去总数的1/5，第二次用去的是第一次的2/3，第二次用去黄沙多少吨？【解答】（4吨）思考一：第一次用去30×1/5＝6吨，第二次用去6×2/3＝4吨。

思考二：第二次用去的占总数的1/5×2/3＝2/15，第二次用去30×2/15＝4吨。

【例题3】晶晶三天看完一本书，第一天看了全书的1/4，第二天看了余下的2/5，第二天比第一天多看了15页，这本书共有多少页？【解答】（300页）第一天看了后剩下1－1/4＝3/4，第二天看的是余下的2/5，第二天看的占总页数的3/4×2/5＝3/10，第二天比第一天多的占总页数的3/10－1/4＝1/20，即总页数的1/20是15页，所以总页数是15÷1/20＝300页。