当前位置：文档之家 › (34)简谐运动的合成

(34)简谐运动的合成

  • 格式：ppt
  • 大小：1.39 MB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

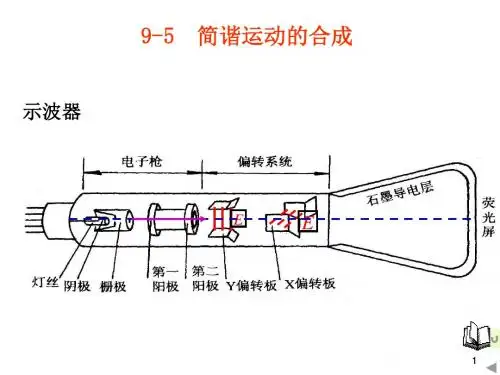
高二物理竞赛课件：简谐运动的合成

高二物理竞赛课件：简谐运动的合成


*四、两个同方向不同频率简谐运动的合成 拍
x1 t
x2 t
x t
拍 合振动振幅 随时间周期性加强与减弱的现象
两个频率较大且相差极小的同方向谐振动合成形成拍
例1 两个同方向简谐振动，周期相同，振幅为 A1=0.05m, A2=0.07m，组成一个振幅为A=0.1044m的简 谐振动，求两个分振动的相位差。
要决定于 = 2- 1
= 0
y A2 x A1
=
y A2 x A1
为 的整数倍，合振动轨迹为直线
= /2
= 3/2
x2 A12
y2 A22
1
为 2的奇数倍，合振动轨迹为正椭圆
= P·/4 .Q = 3/4 = -/4 = -3/4
为其他值，合振动轨迹为斜椭圆
方向： 2 1 0就是顺时针，反之逆时针。
解： A2 ?
A2 A12 A2 2 A1 A cos( 1)
0.1m
A2
2
因为 A2 A12 A22
O
所以
2
1
2
A
2 1
1
1
A1
x
x x1 x2
A
A2
2
O
x 1
A1
x2 x1
பைடு நூலகம்
x
利用解析法也可以计算振幅和初相。
x x1 x2 A1 cost 1 A2 cost 2
A1 cost cos1 sint sin1 A2 cost cos2 sint sin2
A1 cos1 A2 cos2 cost A1 sin1 A2 sin2 sint
x=A1cos( t+ 1) y=A2cos( t+ 2)
简谐运动的合成

简谐运动的合成

所以，拍频是振动 cos(
2
1 2 (
拍频（振幅变化的频率）
2 1
2 t)
的频率的两倍。
2 1
2
) 2 1
8.2
四
简谐运动的合成
第八章 机械振动
两个相互垂直的同频率简谐运动的合成 x A1 cos( t 1 )
y A 2 cos( t 2 )
( k 0 ， 1 ， 2, )
1）相位差 2 1 2 k π
x
o A
A2

x
o
T
1
t
x ( A1 A 2 ) cos( t )
A
A A1 A 2
2 1 2k π
8.2
简谐运动的合成
A
2 1 2 2

x n A n cos( t n )
A
1 A1
x x1 x 2 x n
x A cos( t )
2
A2
A3 3
o
x
多个同方
简谐运动的合成
第八章 机械振动
x 1 A 0 cos t x 2 A 0 cos( t )
2
T π
T
1
2 1
2 1
拍频（振幅变化的频率）
8.2
简谐运动的合成
第八章 机械振动
由于振幅是周期性变化的，所以合振动不再是 简谐振动。
当 与 都很大，且相差甚微时，可将 1 2 2 视为振幅部分，合成振动是以 为角频率的 ( 2 1 ) / 2 近似谐振动。 2 1 1 2
简谐运动的合成

简谐运动的合成

x = ( 2 A1 cos 2 π
ν 2 −ν 1
2
t ) cos 2 π
ν 2 +ν1
2
t
振幅部分 振动频率 ν = (ν 1 + ν 2 ) 2 振幅 A = 2 A1 cos 2 π
合振动频率
ν 2 −ν 1
2
振 动
Amax = 2A1
t
Amin = 0
15
第九章
物理学
第五版
9-5
简谐运动的合成
y
ϕ （1） 2 −ϕ1 = 0或 2 π ） A2 y= x A1
A2
A1
o
x
ϕ （2） 2 − ϕ1 = π ） A2 y=− x A1
第九章 振 动
y
A2
A1
o
x
7
物理学
第五版
9-5
简谐运动的合成
x 2 y 2 2 xy 讨 + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 论 A12 A2 A1 A2
A
ϕ1
ϕ
A 1
O
x2
x1
xx
两个同方向同频率简谐运动合成后仍 两个同方向同频率简谐运动合成后仍 合成 频率的简谐 简谐运动 为同频率的简谐运动
第九章 振 动
2
物理学
第五版
9-5
简谐运动的合成
（1）相位差 ∆ϕ = ϕ 2 − ϕ1 = 2k π (k = 0，1，2,⋯ ） ± ± )
x
ϕ
A2
x
o
y = A2 cos(ωt + ϕ 2 )
椭圆方程） 质点运动轨迹 （椭圆方程）
x 2 y 2 2 xy + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 2 A1 A2 A1 A2
大学物理第五版下册 简谐运动的合成课件

大学物理第五版下册 简谐运动的合成课件


简谐运动能量守 恒，振幅不变
6
第九章
振 动
物理学
第五版
（3） 熟记平均动能和平均势能 ）
E
k
1 1 = E = kA 2 4
2
1 = m ω 2A 4
2
E
P
1 1 = E = kA 2 4
2
1 = m ω 2A 4
2
第九章
振 动
7
物理学
第五版
在实际问题中，经常要遇到一个质点同时参与几种 在实际问题中， 振动的问题。根据运动的叠加原理， 振动的问题。根据运动的叠加原理，此时质点所做的运动 实际上是几种振动的合成。 实际上是几种振动的合成。 的合成问题。 我们仅研究两个同方向的振动的合成问题。
π
点P的相位为 的相位为
ΦP = ω( tP −t0 ) +ϕ = 0
t =0
t =tP
x/m
第九章
振 动
5
物理学
第五版
(3): 根据
ΦP = ω(t P −t0 ) +ϕ = 0
π /3 ω(t P −t 0 ) = ( tP −t0 ) = 3 ω 4. 简谐运动的能量
π
∴ t P =1.6S
（1） 动能 ） （2） 势能 ）
1 2 kA 2 1 1 2 E k = mv = m ω 2 A 2 sin 2 (ωt + ϕ ) 2 2
1 2 1 E p = kx = m ω 2 A 2 cos 2 (ωt + ϕ ) 2 2
1 1 2 2 2 E = E k + E p = m ω A = kA 2 2
x = Acos(ωt +ϕ)
9.8 k g = = =10rad / s 式中 ω = ∆l m 0.098
《简谐运动的合成》课件

《简谐运动的合成》课件


演化、分支和应用
复杂演化
分支学科
摆锤波、庞加莱山丘和分形结构。
天文学、量子力学、金融市场的 年度周期、周期性疾病等。
应用
音乐制作、机械振动隔振等。
《简谐运的合成》PPT 课件
让我们一起探索简谐运动的奥秘，以及如何合成它们，理解它们的物理和声 学意义。
简谐运动
定义
在保证周期性的前提下，物体在固定外力作用下沿一个固定轨道做的运动称为简谐运动。
特点
周期性、振幅、相位、频率、能量守恒。
物理意义
简谐运动是许多自然现象的基础，例如弹簧振子、波的传播、电路中的交流电等。
4 频率
单位时间内重复运动的次数，即振动的快慢。
简谐振动的模拟
Project 1
通过模拟普通化学键中的键弹 性常数，让分子的振动成为一 个弹性团体的整体振动。
Project 2
开发一个可以模拟波的传播和 反射等现象的平台。
Project 3
设计一个工具用于分析在大量 复杂结构和流体下的流动或运 动。
总结
原理 应用 重要性
简谐运动的周期性、振幅、相位、频率、能量守 恒 声音、机械振动、电路等多个领域。
简谐振动学是理解自然现象及应用科学的基础。
力学和声学之美
1 位移
最基本的力学量，表述物体在空间三维坐标 系所占据的位置。
2 振幅
描述物体围绕平衡位置做小幅度振动的最大 位移量。
3 波长
因为波是重复的，所以它有特定的波长。
简谐振动的合成
概述
两个或多个简谐运动的合成。
合成振幅的求法
矢量法或三角函数法。
合成频率的求法
各组分振动的频率之和。
双摆实验
演示简谐振动的合成原理。
第三节 简谐运动的合成

第三节 简谐运动的合成


2 1 2k k 0,1,2,
A1
A A1 A2 合振动加强
A2
若两分振动反相:
2 1 (2k 1) k 0,1,2,
A A1 A2
合振动减弱
若 A1=A2 , 则 A=0
A2
A1
课堂练习：
两个同方向同频率的谐振动，振动方程分别为
x1
6102 cos(5t )m，
2
x2
2102 sin(
t
)
A
ω2t
O
ω2
2
ω1
ω1t
A
(ω 2
A1
ω1)
t
2
2
A
A2 1
A2 2
2A1A2cos(2
1)t
x2 x
x1x1
x2
x
当 (ω2 ω1) t时,2kπ
A 有最大值 A A1 A2
当 (ω2 ω1) t (时2k，1) π
A有最小值 A A1 A2
合振动振幅的频率为: (ω2 ω1) 2π
(2) 0, ,2 (或 )时,退化为直线;
(3) , 3 (或 ) 时,为正椭圆,若A1=A2,则退化
为圆.2 2
2
(4)椭圆轨迹内切于边长为2A1和2A2的矩形; (5)0 时,椭圆顺时针方向转;
0(或 2 ) 椭圆逆时针方向转.
四、相互垂直但频率不同的简谐振动的合成
5t)m
则其合振动的振幅为谐振动,振幅为：
（1）0 ；
（2）4cm；
（3）4 5cm ；
2
（4）8 cm。
二、同方向不同频率谐振动的合成
1. 分振动 : x1 A1 cosω1 t x2 A2 cosω2t
简谐运动的合成

简谐运动的合成


x
A A12 A22 2 A1 A2 cos( 2 1 )
A1 sin 1 A2 sin 2 tan A1 cos1 A2 cos 2
11
x
A1
x
反相
2
o
o
T
减弱
t

A
A2
A A1 A2
2 2
x ( A2 A1 ) cos( t )
A A1 A2 2 A1 A2 cos( 2 1 )
7
*三
多个同方向同频率简谐运动的合成
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
A2
2
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
0
x2
x
1
x1
A1
x
合振动：x x1 x2
o
？
t
3
x1 A1 cos( t 1 ) x2 A2 cos( t 2 )

2
x x1 x2
x A cos( t )
A4 A3 A5 A2 O A6 A x 1
10
小结：
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )

2
A2
1
A
x x1 x2
x A cos( t )

0
A1

xn An cos( t n )
A3 A
1 A1
x x1 x2 xn
x A cos(t )
简谐运动的合成实验

简谐运动的合成实验

简谐运动的合成实验一、 实验目的1. 了解简谐运动的合成理论实现方法。

2. 观察实验现象，了解简谐运动的合成的特点。

3. 学会利用旋转适量法分析简谐运动。

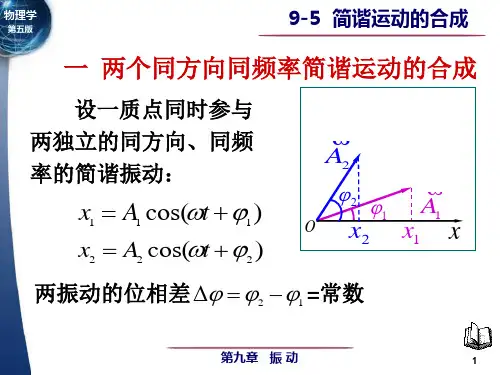
二、 实验原理.1. 两个同方向同频率简谐运动的合成：若两个同方向的简谐运动，它们的角频率都是ω，振幅分别为A1和A2，初相分别是1ϕ和2ϕ，则它们的运动方程分别为x1=A1cos(ωt+1ϕ),x2=A2cos(2ϕω+t ).因为振动是同方向的，所以这两个简谐运动在任何时候的合位移x 仍在同一直线上，而且等于这两个分振动位移的代数和，即 x=x1+x2.。

合位移也可以用旋转矢量法求出。

如图1所示，两分振动的旋转矢量分别为A1和A2，开始时（t=0），它们与ox 轴的夹角分别为1ϕ和2ϕ，在ox 轴上的投影分别为x1及x2.由平行四边形法则，可得和矢量A=A1+A2。

由于A1、A2以相同的ω绕着o 点作逆时针旋转，它们的夹角（12ϕϕ-）在旋转过程中保持不变，所以矢量A 的大小也保持不变，并以相同的角速度ω绕着o 点作逆时针旋转。

从图1中可以看出，任意合矢量A 在ox 轴的投影x=x1+x2，因此和矢量A 即为合振动所对应的旋转矢量，而开始时矢量A 与ox 轴的夹角即为合振动的初相位ϕ。

由图可得合位移为x=Acos(ϕω+t )。

这就表明合振动仍然是简谐运动，其合振幅为A=)12cos(2122*21*1ϕϕ-++A A A A A A 。

合振动的初相位为tan ϕ=(A1sin )2sin 21ϕϕA +)\2cos 21cos 1ϕϕA A +。

图12. 旋转矢量法：从坐标原点O (平衡位置)画一矢量 ，使它的模等于谐振动的振幅A ，并令t=0时A 与x 轴的夹角等于谐振动的初位相φ0，然后使A 以等于角频率ω的角速度在平上绕O 点作逆时针转动，这样作出的矢量称为旋转矢量。

显然，旋转矢量 任一时刻在x 轴上的投影x=Acos(ωt+φ0)就描述了一个谐振动。

简谐运动的合成和分解

简谐运动的合成和分解


y
x
x 2 y 2 2 xy 2 cos( ) sin ( 2 1 ) 2 1 2 2 A1 A2 A1 A2
结论：两相互垂直同频率简谐振动的合成，其振动轨 迹为一椭圆 (又称“椭圆运动” )。椭圆轨迹的形状取 决于振幅和相位差。
x 2 y 2 2 xy 2 2 cos( 2 1 ) sin ( 2 1 ) 2 A1 A2 A1 A2
临界阻尼振动：质点不作往复运动的极限状态.
火炮的阻尼
4-3-2 受迫振动和共振
1. 受迫振动
受迫振动： 系统在周期性的外力持续作用 下所发生的振动。
策动力： 周期性的外力 设：
F F0 cos t
fr f kx
o
x
F
x
由牛顿第二定律
令
2 0
d x dx m 2 kx F0 cos t dt dt
2 1 t ) 随时间缓慢变化 振幅 2 A cos( 2
2 1 t ) 快速变化 谐振因子 cos( 2
第一项缓慢变化，第二项快速变化：“拍(beat)” 调制
拍现象的应用： 用音叉振动校准乐器 测定无线电频率 测定超声波 调制高频振荡的振幅和频率
3. 相互垂直的简谐运动的合成 x方向的谐振动 x A1 cos( t 1 )
讨论：
（1）当 2 1 kπ 时
x 2 y 2 2 xy 2 0 2 A1 A2 A1 A2
x y A A 0 2 1
2
A2 A2 A2 y x : 0，斜率 ； π，斜率 A1 A1 A1 结论： 合振动为线振动，轨迹为 2 2 2 2
x2 A cos(2t )
简谐振动简谐振动的合成课件

简谐振动简谐振动的合成课件


1、细线质量不计
约 定 2、 50 sin
0
3、阻力不计
M m glsin m gl 质点 m 受力如图重力矩： 波动：振动的传播（振动状态的传播）
弹性介质:是指由弹性力组合的连续介质。
二、超声波与次声波及其生物效应
相互垂直的简谐振动的合成
l 根据质点的动量距定理 （2）t =T/4 时，质点的位置、速度、加速度；
• •代数方法：设两个振动具有相同频率，
同一直线上运动，有不同的振幅和初相位
x1(t) A1 cos(t 1)
的仍 简然
x2(t) A2 cos(t 2)
x(t) x1(t) x2(t)
谐是 振同 动频
( A1 cos1 A2 cos2 ) cost。 率
( A1 sin1 A2 sin2 ) sint
质量可忽略的弹簧，一端固定，一端系一有质量的物体，称此系统为弹簧振子。
Ep
xA
X
波传播一个波长的距离所需时间
0
317.
13
1440
（2）波谷经过原点的时刻
（3）第一次通过平衡位置的时刻。
E
与地球、海洋及大气的大规模运动有关。
0
331.
E p Ek
t
x
胡玉才：e-mail
五、阻尼振动 受迫振动 共振
用李萨如图形 在无线电技术 中可以测量频 率：
Tx :Ty 1: 2
在示波器上，垂直方向与水平方向同时 输入两个振动，已知其中一个频率，则 可根据所成图形与已知标准的李萨如图 形去比较，就可得知另一个未知的频率。
0
几幅典型的利萨如图形
1:2
1:3
2:3
2
x :y 2 :1 2
简谐运动的合成.ppt

简谐运动的合成.ppt


2
1
(2k 1)π
2
1
小结
（1）相位差 2 1 2k π
A A A
1
2
(k 0，1，) 加强
（2）相位差
2
1
(2k 1) π
(k 0，1，)
A A A
1
2
减弱
（3）一般情况
A A A A A
1
2
1
2
二 两个相互垂直的同频率的简谐
振幅
A

2 A1 cos2 π 2
1
2
t
Amax 2A1 Amin 0


x (2A1 cos2 π
2
2
1 t)cos2 π
2
2
1t
2π2 1 T π
2
2 1
T 1
2 1
拍频（振幅变化的频率）
方法二：旋转矢量合成法
(2 1)t (2 1)

2A1 A2
cos(2
1 )
x x1 x2

A
x tan
A1
sin
1

A2
sin2
A1 cos1 A2 cos2

A2
2

1
A1
O x2 x1 x
两个同方向同频率简谐运动合成后仍
为同频率的简谐运动
（1）相位差
2
1
2k π
(k
o
A1
A2
A3
A4
A5
A
x
A Ai NA0
x A cos[t (N 1)]

大学物理(9.3.2)--简谐运动的合成





A2
2
o
1 A1
x
多个同方向同频率简谐运动合成仍为简谐
运动
东北大学 理学院 物理系
大学物理 第九单元 振动
第三讲 简谐运动的合成
* 四、两个同方向不同频率简谐运动的合成
x1
拍
t
x2 t
x t
拍 合振动振幅 随时间周期性加强与减弱的现
两 个 频 率 较 大 且 相 差 极 小 的象同 方 向 谐 振 动 合 成 形 成
东北大学 理学院 物理系
大学物理 第九单元 振动
第三讲 简谐运动的合成
3. 两种特殊情况
A
A2 1

A2 2

2 A1 A2
cos( 2
1 )
(1) 若两分振动同相
2 1=2k
(k=0,1,2,…)
则 A=A1+A2 , 两分振动相互加强
(2) 若两分振动反相
2 1=(2k+1)
第三讲 简谐运动的合成
* 三、多个同方向同频率简谐运动的合成
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )

xn An cos(t n )
x x1 x2 xn
x A cos(t )

A
A3
3
A1 sin1 A2 sin2 Asin
A A12 A22 2 A1A2 cos(2 1)
tan

A1 sin1 A1 cos1

A2 A2
sin 2 cos2
x Acos cost Asin sint Acos( t )

简谐运动的合成与分解


两振动的频率只有很小的差异
则可以近似地看做同频率的合成，不过相差在 缓慢地变化，因此合成运动轨迹将要不断地按上 图所示的次序，在图示的矩形范围内自直线变成 椭圆再变成直线等等。
如果两振动的频率相差较 大，但有简单的整数比
则合成运动又具有稳定的 封闭的运动轨迹。这种图 称为李萨如图。
如果已知一个振动的周期，就 可以根据李萨如图形求出另一 个振动的周期，这是一种比较 方便也是比较常用的测定频率 的方法。
阻尼振动（摩擦阻尼，辐射阻尼）
对于摩擦阻尼， 当 不太大时 （ 称为阻尼系数） 由牛顿第二定律
k 2 0 ; 令 m
略讲自学
dx Ft dt
2 m
d2 x dx m 2 kx dt dt
代入上式（ 称为阻尼因子）
在阻尼较小时， < 0，
三、两个互相垂直同频率简谐振动的合成
x1 A1 cos(t 10 )
y2 A2 cos(t 20 )
消去 t 得到轨道方程 （椭圆方程）
x2 y2 xy 2 2 cos( ) sin (20 10 ) 20 10 2 2 A1 A2 A1 A2 20 10 20 10 0
如果两振动的频率相差较大但有简单的整数比在自然界和工程技术中我们所遇到的振动大多不是简谐振动而是复杂的振动处理这类问题往往把复杂振动看成由一系列不同频率的间谐振动组合而成也就是把复杂振动分解为一系列不同频率的间谐振动这样分解在数学上的依据是傅立叶级数和傅立叶积分的理论因此这种方法称为傅立叶分析
本讲主要内容：
着重研究1 , 2相近情况
即 1- 2 << 1 or 2
——拍现象（Beat)

简谐振动的合成


(A1 sin1 A2 sin2 )sint
合振幅
令： A1 cos1 A2 cos2 Acos 代入上式：
A1 sin1 A2 sin2 Asin
2
x ( A1 cos1 A2 cos2)cost (A1 sin1 A2 sin2 )sint
Acos cost Asin sint Acos(t ) x Acos(t )
x1(t) a cost
M aN
x2 (t) a cos(t ) x3(t) a cos(t 2 )
C
R N
A
a3
xN (t) a cos[t (N 1) ]O a1 P
在COM中：A 2R sin(N / 2)
上两式相除得：
在OCP中： a 2Rsin( / 2)
7
A a sin(N / 2) sin / 2
若 A1 A2, A 2A1
2.当 2 1 （2k 1） (k 0,1,2, ) 时,
A
A12
A
2 2
2 A1
A2
cos(
2
1
)
| A1 A2 | 合振动振幅最小。
若 A1 A2, A 0
A2
3.一般情况 | A1 A2 | A | A1 A2 |
5
A A2 A1
A2 A A1 A A1
第二节
简谐振动的合成
1
一、同方向同频率简谐振动的合成
在同一直线上同频率的两个简谐振
动分别为：
x1 A1 cos(t 1),
x2 A2 cos( t 2 )
• 代数方法： 振动合成
x x1 x2 A1 cos(t 1) A2 cos(t 2 )
(A1 cos1 A2 cos2) cost

大学物理简谐运动的合成

大学物理简谐运动的合 成
目录
• 简谐运动的定义与特性 • 简谐运动的合成原理 • 简谐运动的合成方法 • 简谐运动的合成应用 • 总结与展望
简谐运动的定义与特
01
性
简谐运动的定义
简谐运动
物体在平衡位置附近做往复运动，其位移、速度和加速度随时间按正弦或余弦 规律变化的运动。
简谐运动的数学描述
简谐运动可以用正弦或余弦函数表示，其数学表达式为 $x = Asin(omega t + varphi)$，其中 $A$ 是振幅，$omega$ 是角频率，$varphi$ 是初相。
简谐运动的特性
周期性
简谐运动具有周期性，即物体在每个周期内重复 相同的运动轨迹。
往复性
简谐运动是往复运动，即物体在平衡位置附近来 回振动。
能量守恒
简谐运动过程中，系统的动能和势能相互转化， 总能量保持不变。
简谐运动的分类
自由振动
不受外力作用的简谐运动。
受迫振动
受到周期性外力作用的振动，其振动频率与外力频率 相同或相近。
简谐运动的合成方法
03
旋转矢量法
总结词
旋转矢量法是一种直观且易于理解的方法，用于合成简谐运动。
详细描述
旋转矢量法是通过引入一个旋转矢量来表示简谐运动，该矢量在复平面内以角速 度旋转。通过旋转矢量的长度和角度变化，可以直观地理解简谐运动的合成过程 。
复数法
总结词
复数法是一种基于复数运算的方法，用于合成简谐运动。
自激振动
由系统内部激励产生的振动，不需要外部激励作用。
02
简谐运动的合成原理
线性合成原理
线性合成原理是指两个简谐运动的合成结果仍为简谐运动，其振幅和角频率分别为两个简谐运动振幅 和角频率的线性组合。

物理-相互垂直的简谐运动的合成


y A2 x A1
质点离开 平衡位置 的位移
r(t) A12 A22 cos(t 1 )
y
A2
o A1 x
合振动是与分振动同频率的简谐振动
一、两个相互垂直的谐振动的合成
x A1
2
y A2
2
2xy cos(2 A1 A2
1 )
s in2 ( 2
1 )
(3)
若
2
1
2
x2 A12
y2 A22
合运动的 轨道方程
( x )2 ( y )2 2xycos sin2
A1
A2
A1 A2
其中： (2 1 )t (2 1 ) ——随时间变化
一般情况下，合运动的轨迹是不稳定的。
一、两个相互垂直的谐振动的合成
分振动： x A1 cos(ω1t φ1 ) y A2 cos(ω2t φ2 )
二、振动频谱分析
数学上已经证明：
任意周期函数（周期为T）：x(ωt) 其中 ω 2π /T
均可展开为三角级数
基频
x(ωt ) a0 (ak cos kωt bk sin kωt )
k 1
k次谐频
1 T/2
a0 T
f (ωt )dt
T / 2
2
ak T
T /2
f (ωt)cos kωtdt (k 0)
x A1
2
y A2
2
2xy cos(2
A1 A2
1 )
s in2 ( 2
1 )
合运动一般是在 x A1, y A2 范围内的一个椭圆。
一、两个相互垂直的谐振动的合成
2
2
x A1
y A2

简谐运动的合成


(2)若另有一振动x3 0.07cos10t 0 ，问0为何值时，
x1 x3的振幅为最大；问0为何值时，x2 x3的振幅为最小。
解：根据题意，画出旋转矢量图
A A12 A22
0.052 0.062
A1
0.078(m)
0 10 0
0 =10
3 4
时，x1
x3的振幅最大
A
A2
tan
A1 sin 1 A1 cos1
A2 A2
sin 2 cos2
讨论 A A12 A22 2 A1A2 cos(2 1)
0，1， 2,)
合振幅最大
A A1 A2
xx
oo
A1 A2
t
A
A A12 A22 2 A1 A2 cos(2 1)
2、两个分振动的相位反相：
相位差 2 1 (2k 1)π (k 0，1,)
合振幅最小 A A1 A2
x
x
A1
2
o
o
t
A
A2
例题 有两个同方向、同频率的简谐振动，它们 的振动表式（SI制）为：
x1
0.05
cos
10t
3 4
x2
0.06 cos 10t
1 4
(1)求它们合成振动的振幅。
简谐运动的合成
一、同方向、同频率两个简谐运动的合成
x1 A1 cos( t 1 )
A2
Q
A
x2 A2 cos( t 2 )
用旋转矢量法求合运动
2 1
P A1
O x2
x1 x
X
合振动位移为： x x1 x2 两个同方向同频率简谐运
x A cos( t ) 动合成后仍为简谐运动
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

机械振动
四 两个相互垂直的同频率简谐运动的合成
x A1 cos(t 1)
y A2 cos(t 2 )
质点运动轨迹 （椭圆方程）
x2 A12

y2 A22

2xy A1 A2
cos(2
1 )

sin2 (2
A2 y
1 )
讨论 1）2 1 0 或 2π
y A2 x A1
tan A1 sin 1 A2 sin 2
两个同方向同频 率简谐运动合成
A1 cos1 A2 cos2 后仍为简谐运动
（34）简谐运动的合成
机械振动
讨论 A A12 A22 2A1A2 cos(2 1) 1）相位差 2 1 2kπ (k 0，1， 2,)
机械振动
4. 有两个同方向、同频率的简谐运动，其合振幅为A=0.20m，
合振动的相位与第一个振动的相位差为π /6，若第一个振动的振幅
为A1=0.173m 。求第二个振动的振幅和两振动的相位差。
解：采用旋转矢量合成图求解。取第一个振动的旋转矢量A1沿x 轴，令其初位相为0；由题意，合振动的旋转矢量A与A1之间的 夹角π /6 。根据矢量合成法则，可得第二个振动的旋转矢量的
(2)若有另一同方向、同频率的简
谐运x3=0.07cos(10t+3)m，则3为多 少时，x1+x3的振幅最大？又3为多少
时，x2+x3的振幅最小？

A

A1 1
A2
2
o
x
解:(1)同方向，同频率的简谐运动合振动振幅为
A A12 A22 2 A1A2 cos( / 2) 7.8102 m
分振动 x1 Acos(1t ) 初相相同 x2 Acos(2t )
合振动 x x1 x2
x 2Acos( 2 1 )t cos( 2 1 t )
2
2
合振动不是简谐振动
当21时,2 1 2 1 则：x A(t)cos t
合振动初相位
tg A1 sin 1 A2 sin 2 11 则： 1.48rad或1.48rad
A1 cos1 A2 cos2
1.48rad
（34）简谐运动的合成
机械振动
(2)要使x1+x3振幅最大，需两振动同相，即 2k
AA31 1
式中
A(t) 2Acos( 2 1 ) t
2 cos t cos( 2 1 )t
2
随t 缓变 随t 快变
频率较大而频率之差很小的两个同方向简谐运动的
合成，其合振动的振幅时而加强时而减弱的现象叫拍.
（34）简谐运动的合成
机械振动
“拍”可看作振幅缓变的简谐振动
拍频 : 单位时间内强弱变化的次数 =|2-1|
（34）简谐运动的合成
机械振动
方法二：旋转矢量合成法
(2 1)t (2 1)
2t 2
2 A2
1t 1 o
x2

A
1
A1
x1
2 1
x
x
A
A2 1

A2 2

2A1 A2
cos
1 2 0
(2 1)t (2 1) 2π ( 2 1)t
（34）简谐运动的合成
机械振动
A
A2 1

A2 2

2A1 A2
cos
(2 1)t
振幅 A A1 2(1 cos)

2 A1 cos(2
1
2
t)
拍频 2 1
(2 1)t
A 2
A2
o x2
1 A1
x1
x
x
1t 2t 2 1

A2
2
1 A1
多个同方向同频率简谐运动合成仍为简谐运动
（34）简谐运动的合成
x1 A0 cost
x2 A0 cos(t ) x 3 A0 cos(t 2 )
机械振动
A o
A1
A2
A3
A4
A5
x
A Ai NA0
xN A0 cos[t (N 1) ]
1） 2kπ
讨 论
(k 0,1,2,)
2）N 2k 'π
(k' kN, k' 1,2,)
N个矢量依次相接构
i A4

A3

A5
A6
O
A1
A2

x
成一个闭合的多边形 .
A0
（34）简谐运动的合成
机械振动
三 两个同方向不同频率简谐运动的合成
cos(t

π 2
)
A2 y
o A1 x
（34）简谐运动的合成
用 旋 转 矢 量 描 绘 振 动 合 成 图
机械振动
（34）简谐运动的合成
两
相
互 垂 直 同 频 率 不 同 相
简 谐 运 动 的 合 成 图
位
差
机械振动
（34）简谐运动的合成
机械振动
五 两相互垂直不同频率的简谐运动的合成
x A1 cos(1t 1)
（拍在声学和无线电技术中的应用）
Hale Waihona Puke 振动圆频率 cost x1 x2
A
1 2
2
（34）简谐运动的合成
机械振动
习题、 怎样利用拍音来测定一音叉的频率?
找一个已知频率1的音叉,同时敲击两音叉产
生拍,测出拍的频率, 根据 2 1
求出被测音叉的频率2.
（34）简谐运动的合成
ox
A1
（34）简谐运动的合成
机械振动
x2 A12

y2 A22

2xy A1 A2
cos(2
1 )

sin2 (2 1)
y
2） 2 1 π
y A2 x A1
3）2 1 π 2
x A2
o A1
x2 A12

y2 A22
1
x A1 cost
y

A2
y A2 cos(2t 2 )
1 0
2

0, π 8
,π 4
, 3π 8
,π 2
李萨如图
1 m 2 n
测量振动频率 和相位的方法
（34）简谐运动的合成
机械振动
3. 已知两同方向、同频率的简谐运动的运动方程分别为 x1=0.05cos(10t+0.75π)m; x2=0.06cos(10t+0.25π)m。 求：(1)合振动的振 幅和初相；
大小（即振幅）为
A2
A12
A2 2 A1 A
cos
A2
0.10m
A2
0.10m
A 0.20m
A
由于A1、A2、A的量值恰好满 足勾股定理，故A2与A1垂直， 即第二个振动与第一个振动的
相位差为

0
A1
A1 0.173m

2
（34）简谐运动的合成
机械振动
二 多个同方向同频率简谐运动的合成
x1 A1 cos(t 1)
x2 A2 cos(t 2 )
xn An cos(t n )
x x1 x2 xn
x Acos(t ) o


A A3
3
x

o
o
A
A2
Tt
（34）简谐运动的合成
机械振动
1）相位差 2 1 2kπ (k 0，1，)
A A1 A2
相互加强
2）相位差 2 1 (2k 1)π (k 0，1，)
A A1 A2 相互削弱
3）一般情况
A1 A2 A A1 A2
o
x
则：3 1 2k 2k 0.75 , k 0,1,2
要使x2+x3振幅最小，需两振动反相，即 (2k 1)
A2
2
o
x

A3
则：3 2 (2k 1) 2k 1.25 , k 0,1,2
（34）简谐运动的合成
A A1 A2
xx
o
o
A1
A2
A
Tt
（34）简谐运动的合成
机械振动
A A12 A22 2A1A2 cos(2 1) 2）相位差 2 1 (2k 1)π (k 0，1, )
A A1 A2 如 A1=A2 , 则 A=0
x
x

A1
2
（34）简谐运动的合成
机械振动
一 两个同方向同频率简谐运动的合成
x1 A1 cos(t 1)

x2 A2 cos(t 2 )
A2

A
x x1 x2
x Acos(t )
x 0
x2 2 1
x1A1
x
A A12 A22 2A1A2 cos(2 1)