余弦定理公式大全

余弦定理公式大全余弦定理是解决三角形问题时经常使用的重要公式，可以通过它计算三角形的边长或角度。

它的表达式是：c² = a² + b² - 2ab*cos(C)其中，a、b、c分别代表三角形的边长，C代表夹在边a和边b之间的角度。

1.角度公式：根据余弦定理公式，我们可以解出夹在边a和边b之间的角度C的值：cos(C) = (a² + b² - c²) / 2ab通过这个公式，如果我们已知三角形的三个边长a、b、c，就可以计算出夹在边a和边b之间的角度C的大小。

2.边长公式：根据余弦定理公式，我们可以解出边c的值：c = √(a² + b² - 2ab*cos(C))通过这个公式，如果我们已知三角形的两个边长a、b和夹在边a和边b之间的角度C，就可以计算出边c的长度。

3.面积公式：根据余弦定理公式，我们可以推导出三角形的面积公式：S = 1/2 * a * b * sin(C)其中，S代表三角形的面积。

通过这个公式，如果我们已知三角形的两个边长a、b和夹在边a和边b之间的角度C，就可以计算出三角形的面积。

4.费马定理公式：根据余弦定理公式，我们可以推导出费马点定理公式：AF² + BF² + CF² = 4S² / sqrt(3)其中，AF、BF、CF分别代表三角形的三个顶点到费马点的距离，S代表三角形的面积。

通过这个公式，如果我们已知三角形的面积S，就可以计算出费马点到三个顶点的距离。

总结：余弦定理提供了一种解决三角形问题的强大工具。

通过余弦定理公式，我们可以计算三角形的边长、角度和面积等相关参数。

这些公式的应用范围非常广泛，是解决三角形问题时的基础知识之一、掌握了余弦定理公式，我们就可以快速准确地解决三角形相关的数学问题。

正余弦公式大全正余弦公式大全：1.正弦函数：正弦函数的公式是：y=sinθ，其中θ表示弧度。

2.余弦函数：余弦函数的公式为：y=cosθ，其中θ表示弧度。

3.正切函数：正切函数的公式为：y=tgtθ，其中θ表示弧度。

4.反正弦函数：反正弦函数的公式为：y= sin-1x，其中x表示反正弦函数的自变量。

5.反余弦函数：反余弦函数的公式为：y=cos-1x，其中x表示反余弦函数的自变量。

6.反正切函数：反正切函数的公式为：y=tg-1x，其中x表示反正切函数的自变量。

7.正割函数：正割函数的公式为：y=secθ，其中θ表示弧度。

8.余割函数：余割函数的公式为：y= cscθ，其中θ表示弧度。

9.余切函数：余切函数的公式为：y=cotθ，其中θ表示弧度。

10.反正割函数：反正割函数的公式为：y=sec-1x，其中x表示反正割函数的自变量。

11.反余割函数：反余割函数的公式为：y=csc-1x，其中x表示反余割函数的自变量。

12.反余切函数：反余切函数的公式为：y=cot-1x，其中x表示反余切函数的自变量。

正余弦公式的应用：1.三角恒等式：三角恒等式的公式可以为：sinθ=cosθ，tgtθ=secθ，cotθ=cscθ。

2.三角函数关系式：三角函数关系式的公式可以为：sin2θ+cos2θ=1，tan2θ+1=sec2θ，cot2θ+1=cscy2θ。

3.振动函数：振动函数表达式可以为：Y=Asinωt+b，其中A表示振幅，ω表示角频率，t表示正余弦函数的自变量，b表示相位移动量。

4.几何图形：几何图形的表示式可以为：X=Acos(ωt+θ)，Y= Asin(ωt+θ)，其中A表示振幅，ω表示角频率，t表示正余弦函数的自变量，θ表示相位移动量。

5.振动和回荡解一元二次方程：一般形式：at2+bt+c=0，其中a，b，c是常量，而t表示根号式振动解，可以化为：t=(-b±√b2-4ac)/2a,其中“±”代表正负号。

余弦定理6个公式
余弦定理，是描述三角形中三边长度与一个角的余弦值关系的数学定理，是勾股定理在一般三角形情形下的推广。

用余弦定理求三角形面积是常见的数学问题，但是想要快速的算出三角形的面积，还需要牢记余弦定理求三角形的面积的公式。

余弦定理有三个公式，三角形ABC中，如果∠A，∠B，∠C的对边分别用a、b、c来表示那么就有如下关系：
在三角形ABC中，角A，B，C的对边分别为a，b，c。

则有：
正弦定理：a/SinA=b/SinB=c/SinC=2R(R为三角形外接圆半径)
余弦定理：a^2=b^2+c^2-2bc*CosA b^2=a^2+c^2-2ac*CosB
c^2=a^2+b^2-2ab*CosC
余弦定理变形公式：cosA=(b^2+C^2-a^2)/2bC
cosb=(a^2+c^2-b^2)/2aC cosC=(a^2+b^2-C^2)/2ab
注：勾股定理其实是余弦定理的一种特殊情况。

cos公式的其他资料：
它是周期函数，其最小正周期为2π。

在自变量为2kπ（k为整数）时，该函数有极大值1；在自变量为（2k+1）π时，该函数有极小值-1，余弦函数是偶函数，其图像关于y轴对称。

余弦定理公式及变形公式好的，以下是为您生成的关于“余弦定理公式及变形公式”的文章：在咱们学习数学的这趟奇妙旅程中，余弦定理就像是一把神奇的钥匙，能帮咱们打开好多难题的大门。

先来说说余弦定理的基本公式吧，对于一个三角形，假设三条边分别是a、b、c，对应的角分别是A、B、C，那么余弦定理的公式就是：a² = b² + c² - 2bc·cosA，b² = a² + c² - 2ac·cosB，c² = a² + b² - 2ab·cosC。

就拿我之前给学生讲题的时候遇到的一个例子来说。

有一次，课堂上我出了这样一道题：一个三角形，两条边分别是 3 和 4，它们夹角的余弦值是 1/8 ，让大家求第三条边。

同学们一开始都有点懵，不知道从哪儿下手。

我就引导他们，这时候余弦定理就派上用场啦！根据余弦定理 a² = b² + c² - 2bc·cosA，咱们把数值代入进去，就得到 a² = 3² + 4² - 2×3×4×(1/8) ，经过计算，就能得出 a 的值。

再来说说余弦定理的变形公式。

通过基本公式进行一些推导和变换，咱们能得到好多有用的变形。

比如 cosA = (b² + c² - a²) / (2bc)，cosB = (a² + c² - b²) / (2ac)，cosC = (a² + b² - c²) / (2ab) 。

这些变形公式在解题的时候可好用啦。

有一回，我带学生们做练习题，有一道题是只知道三角形的三条边的长度，让求其中一个角的余弦值。

这时候，用变形公式就能轻松解决。

直接把边的长度代入变形公式，就能算出角的余弦值。

余弦定理及其变形公式
嘿，朋友们！今天咱来聊聊超厉害的余弦定理及其变形公式哟！
余弦定理就是：$a^2=b^2+c^2-2bc\cos A$，就好比你要去一个地方，$a$是你走的路程，$b$和$c$是两条不同的路，而$\cos A$就是它们之间的关系呀！比如说，在一个三角形里，已知两边长度是 3 和 4，夹角是60 度，那就能用这个公式算出第三边的长度啦！
还有变形公式呢，比如$\cos A=\frac{b^2+c^2-a^2}{2bc}$，这就像你找到了一个神奇的密码，能通过已知条件算出角度哟！好比你知道了三边的长度，就能通过这个公式算出角的大小啦！嘿，你说神奇不神奇！
咱再举个例子，想象一下，在一个神秘的三角形世界里，你要找到一个特定角的大小，这时候这些公式不就像你的秘密武器一样么！哇塞，学会了这些，就像是掌握了打开三角形宝藏大门的钥匙呀！是不是超级有趣呀！赶紧去试试吧！。

三角形正弦定理和余弦定理公式三角形正弦定理公式可表述为：在任意三角形ABC中，设三个边的长度分别为a，b，c，对应的角度为A，B，C，则有以下关系：a/sinA = b/sinB = c/sinC
三角形余弦定理公式可表述为：在任意三角形ABC中，设三个边的长度分别为a，b，c，对应的角度为A，B，C，则有以下关系：a² = b² + c² - 2bc*cosA
b² = a² + c² - 2ac*cosB
c² = a² + b² - 2ab*cosC
这两个定理是解决三角形问题中常常使用的定理，可以用于计算缺失的边长或角度大小，以及求解三角形的各种性质。

拓展：这两个定理在解决三角形问题时起到了重要作用，但是也有一些特殊情况的应用。

比如，当角A=90°时，余弦定理可以简化为勾股定理：
c² = a² + b²
也就是著名的勾股定理。

此外，正弦定理和余弦定理也可以用于
解决其他类型的几何问题，比如用于求解四边形的面积或角度。

同时，这两个定理还可以推广到高维空间中的三角形，称为n维三角学。

余弦定理公式6个余弦定理是解决三角形中边长和角度之间关系的重要工具。

它可以帮助我们计算未知的边长或角度，从而更好地理解和分析三角形。

1. 第一个余弦定理公式是用于计算三角形边长的公式。

若三角形的边长分别为a、b和c，而对应的内角为A、B和C，则余弦定理可以表达为：c = a + b - 2abcos(C)。

这个公式可以帮助我们计算未知边长，只需要已知两个边长和它们之间的夹角即可。

2. 第二个余弦定理公式是用于计算三角形内角的公式。

若三角形的边长分别为a、b和c，而对应的内角为A、B和C，则余弦定理可以表达为：cos(C) = (a + b - c) / 2ab。

这个公式可以帮助我们计算未知角度，只需要已知三个边长即可。

3. 第三个余弦定理公式是用于计算三角形面积的公式。

若三角形的边长分别为a、b和c，而对应的内角为A、B和C，则余弦定理可以表达为：Area = 0.5 * ab * sin(C)。

这个公式可以帮助我们计算未知面积，只需要已知两个边长和它们之间的夹角即可。

4. 第四个余弦定理公式是用于判断三角形形状的公式。

若三角形的边长分别为a、b和c，则余弦定理可以表达为：c < a + b，如果等号成立，则表示三角形是直角三角形；如果等号不成立，则表示三角形是锐角三角形；如果等号反向成立，则表示三角形是钝角三角形。

5. 第五个余弦定理公式是用于计算三角形的高度的公式。

若三角形的边长分别为a、b和c，而对应的内角为A、B和C，则余弦定理可以表达为：h = b * sin(A)，其中h表示三角形的高度。

这个公式可以帮助我们计算未知高度，只需要已知一个边长和它对应的角度即可。

6. 第六个余弦定理公式是用于计算三角形的周长的公式。

若三角形的边长分别为a、b和c，则余弦定理可以表达为：Perimeter = a + b + c。

这个公式可以帮助我们计算未知周长，只需要已知三个边长即可。

综上所述，余弦定理提供了多种公式和方法来解决三角形中的边长和角度之间的关系。

三角函数公式大全详解一、什么是三角函数？三角函数是一类函数，它们以三角形为基本图形，通过三角形任意两条边和它们之间的夹角代表某一比例关系。

它们是以平面角度（θ）来描述某一比例关系，可以将角度θ在特定范围内运用到具有实际意义的函数中，比如描述的是三角形的大小或形状。

二、三角函数的九大公式（正弦定理、余弦定理、正切定理）1. 正弦定理：a2=b2+c2-2bccosA（a、b、c分别表示三角形的三边的长度，A表示夹角）；2. 余弦定理：a2=b2+c2-2accosB（a、b、c分别表示三角形的三边的长度，B表示夹角）；3. 正切定理：tanA/tanB=tan(A+B)/tan(A-B)（A、B分别表示三角形两个内角的大小）；4. 正弦函数：y=sinx（x为角度，sinx表示一个三角形的第三边与夹角的长度的比率）；5. 余弦函数：y=cosx（x为角度，cosx表示一个三角形的第二边与夹角的长度的比率）；6. 正切函数：y=tanx（x为角度，tanx表示一个三角形第一边与夹角的长度的比率）；7. 余切函数：y=cotx（x为角度，cotx表示一个三角形第一边与夹角的长度相反的比率）；8. 正割函数：y=secx（x为角度，secx表示一个三角形第二边与夹角的长度的比值的倒数）；9. 余割函数：y=cscx（x为角度，cscx表示一个三角形第三边与夹角的长度的比值的倒数）。

三、三角函数的反函数1. 反正弦函数：y=arcsinx（x表示一个三角形的第三边与夹角的长度之比，arcsinx表示求三角形夹角的大小θ）；2. 反余弦函数：y=arccosx（x表示一个三角形的第二边与夹角的长度之比，arccosx表示求三角形夹角的大小θ）；3. 反正切函数：y=arctanx（x表示一个三角形第一边与夹角的长度之比，arctanx表示求三角形夹角的大小θ）；4. 反余切函数：y=arccotx（x表示一个三角形第一边与夹角的长度相反的比率，arccotx表示求三角形夹角的大小θ）；5. 反正割函数：y=arcsecx（x表示一个三角形第二边与夹角的长度的倒数，arcsecx表示求三角形夹角的大小θ）；6. 反余割函数：y=arccscx（x表示一个三角形第三边与夹角的长度的倒数，arccscx表示求三角形夹角的大小θ）。

三角函数诱导公式正弦定理余弦定理基本公式1.三角函数诱导公式：正弦诱导公式：sin(a ± b) = sin(a)cos(b) ± cos(a)sin(b)余弦诱导公式：cos(a ± b) = cos(a)cos(b) ∓ sin(a)sin(b)正切诱导公式：tan(a ± b) = (tan(a) ± tan(b))/(1 ∓ tan(a)tan(b))这些诱导公式可以用来简化计算，将三角函数的运算转化为其他三角函数的运算，从而简化复杂的计算过程。

2.正弦定理：正弦定理用于求解具有三个边的三角形的角度。

根据正弦定理，三角形的三个边的比例等于其对应角度的正弦值的比例。

正弦定理的公式如下：a/sin(A) = b/sin(B) = c/sin(C)其中，a、b、c为三角形的三个边的长度，A、B、C为对应的三个角的度数。

正弦定理可以通过三边求角、两边一角求边等问题中使用。

3.余弦定理：余弦定理用于求解具有三个边或两边一角的三角形的边长。

根据余弦定理，三角形的一个边的平方等于另外两边的平方的和减去这两边长度的乘积与这两边所夹角的余弦值的两倍的乘积。

余弦定理的公式如下：c² = a² + b² - 2abcos(C)其中，a、b、c为三角形的三个边的长度，C为夹在a、b之间的角的度数。

余弦定理可以通过三边求角、两边一角求边等问题中使用。

4.基本三角函数公式：基本三角函数公式包括正弦、余弦、正切的定义和性质。

正弦公式：sin(a) = opposite/hypotenuse = a/c余弦公式：cos(a) = adjacent/hypotenuse = b/c正切公式：tan(a) = opposite/adjacent = a/b其中，a、b为直角三角形的两个直角边的长度，c为斜边的长度。

这些基本公式在解决直角三角形问题中非常常用。

高中余弦定理公式大全高中余弦定理公式是三角学中的重要定理之一，用于求解三角形的边长或角度。

它是基于三角形的三条边之间的关系而得出的。

余弦定理公式可以表示为：c = a + b - 2ab cos(C)其中，a、b、c 分别表示三角形的三条边的长度，C 表示夹在 a 和 b 之间的角的大小。

在使用余弦定理时，需要注意以下几点：1. 余弦定理适用于任意三角形，不仅仅是直角三角形。

2. 当 C 是直角时，余弦定理可以简化为勾股定理：c = a + b。

3. 当 C 是锐角时，cos(C) 大于 0；当 C 是钝角时，cos(C) 小于 0；当 C 是180度时，cos(C) 等于 -1。

这个性质可以用来判断三角形是锐角三角形、钝角三角形还是直角三角形。

4. 余弦定理也可以用来求解三角形的角度，当已知三边长度 a、b、c 时，可以通过余弦定理反解出角度 C 的大小。

除了上述提到的余弦定理公式，高中三角学中还有一些类似的公式，如正弦定理和正切定理。

这些公式在解决不同类型的三角形问题时都有其特定的应用。

正弦定理公式可以表示为：a/sin(A) = b/sin(B) = c/sin(C)其中，a、b、c 分别表示三角形的三条边的长度，A、B、C 分别表示与对应边相对的角的大小。

正切定理公式可以表示为：tan(A) = a/b, tan(B) = b/a其中，a、b 分别表示三角形的两条边的长度，A、B 分别表示与对应边相对的角的大小。

这些定理的掌握和运用可以帮助我们更好地理解和解决三角形相关的数学问题，例如求解三角形的边长、角度或者判断三角形的形状。

三角形边与角的关系公式大全
三角形边与角的关系公式大全包括：
1、三角形内角和公式：三个内角之和等于180°，即A+B+C=180°；
2、余弦定理：在任意三角形中，每条边的平方等于其他两条边的乘积，再减去2乘以这两条边的乘积乘以余弦值，即：a²=b²＋c²－
2bc·cosA；
3、正弦定理：任意三角形中，每条边的正切等于其他两条边的比例，
再乘以这两条边的正切，即：tanA=b/c·tanB；
4、正弦定理：任意三角形中，每条边的正切等于其他两条边的比例，
再乘以这两条边的正切，即：sinA/a=sinB/b=sinC/c；
5、余切定理：任意三角形中，每条边的余切等于其他两条边的比例，
再乘以这两条边的余切，即：cotA=b/c·cotB；
6、面积公式：在任意三角形中，其面积S等于这三条边的一半乘以它
们的乘积的根号，即：S=√(p(p-a)(p-b)(p-c))；其中p为边a、b、c
的半周长，即p=(a+b+c)/2。

正弦余弦定理公式
正弦定理：设三角形的三边为a b c，他们的对角分别为a b c，外接圆半径为r，则称关系式a/sina=b/sinb=c/sinc为正弦定理。

余弦定理：设三角形的三边为a b c，他们的对角分别为a b c，则称关系式，a^2=b^2+c^2-2bc*cosa。

正弦定理：设三角形的三边为a b c，他们的对角分别为a b c，外接圆半径为r，则称关系式a/sina=b/sinb=c/sinc为正弦定理。

余弦定理：设立三角形的三边为a b c，他们的对角分别为a b c，则表示关系式
a^2=b^2+c^2-2bc*cosa
b^2=c^2+a^2-2ac*cosb
c^2=a^2+b^2-2ab*cosc。

证明：
任意三角形abc，作abc的外接圆o。

并作直径bd交⊙o于d，相连接da.
因为直径所对的圆周角是直角，所以∠dab=90度，
因为同弧所对的圆周角成正比，所以∠d等同于∠c。

所以c/sinc=c/sind=bd=2r。

相似可以证其余两个等式。

余弦定理公式1. 引言余弦定理是解决三角形中边长和角度之间关系的重要定理之一。

它可用于计算三角形的边长或角度，为解决各种实际问题提供了有效的工具。

本文将介绍余弦定理的原理、公式及其应用。

2. 余弦定理的原理余弦定理基于三角形中的角余弦定义。

在一个三角形中，我们可以使用余弦定理计算任意一边的平方与另外两边的关系。

余弦定理的基本原理如下：对于一个三角形ABC，设边长分别为a，b，c，对应的角为A，B，C。

那么余弦定理可以表示为以下形式：a² = b² + c² - 2bc * cos(A)类似地，我们可以根据需要选择其他两条边的关系。

3. 余弦定理的公式根据余弦定理的原理，我们可以总结出三个公式：•当需要计算边a时：a = sqrt(b² + c² - 2bc * cos(A))•当需要计算边b时：b = sqrt(a² + c² - 2ac * cos(B))•当需要计算边c时：c = sqrt(a² + b² - 2ab * cos(C))根据余弦定理的这三个公式，我们可以根据已知的数据计算出未知边的长度。

4. 余弦定理的应用余弦定理可以应用于各种实际问题中，例如计算位置坐标、测量距离等等。

4.1 三角形的边长计算假设我们知道一个三角形的两条边的长度和它们之间的夹角，可以使用余弦定理计算出第三条边的长度。

这对于测量无法直接获得的边长非常有用。

4.2 角的计算如果我们知道一个三角形的三条边的长度，并且我们想计算出其中一个角的大小，也可以使用余弦定理解决这个问题。

通过重排余弦定理公式并使用反余弦函数，我们可以计算出角度的值。

4.3 相似三角形的判定余弦定理还可以用于判断两个三角形是否相似。

如果两个三角形的对应边长比例相等，那么它们就是相似三角形。

通过使用余弦定理进行计算，我们可以得出两个三角形的边长比例，从而判断它们是否相似。

余弦定理编辑
余弦定理，是描述三角形中三边长度与一个角的余弦值关系的数学定理。

是勾股定理在一般三角形情形下的推广模式。

余玄定理
表达式
cos A=(b²+c²-a²)/2bc[1]
欧几里得
余弦定理是解三角形中的一个重要定理，可应用于以下两种需求：
当已知三角形的两边及其夹角，可由余弦定理得出已知角的对边。

当已知三角形的三边，能够由余弦定理得到三角形的三个内角。

求边
余弦定理公式可变换为以下形式所以，如果知道了三角形的两边及其夹角，可由余弦定理得出已知角的对边。

求角
余弦定理公式可变换为以下形式所以，如果已知三角形的三条边，能够由余弦定理得到三角形的三个内角。

证明编辑
三角函数证明
如上图所示，△ABC，在c上做高，根据射影定理，可得到：
将等式同乘以c得到：
使用同样的方式能够得到：
将两式相加：
向量证明
中，
，
，
：。

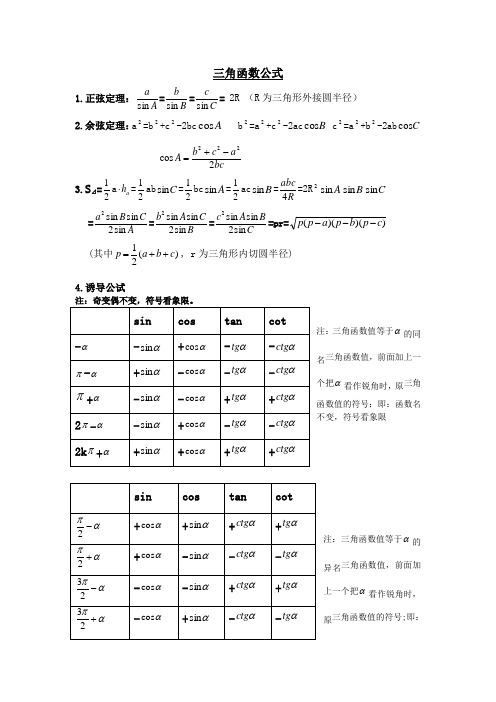
三角函数公式1.正弦定理：A a sin =B b sin =Cc sin = 2R （R 为三角形外接圆半径） 2.余弦定理：a 2=b 2+c 2-2bc A cos b 2=a 2+c 2-2ac B cos c 2=a 2+b 2-2ab C cosbca cb A 2cos 222-+=3.S ⊿=21a a h ⋅=21ab C sin =21bc A sin =21ac B sin =Rabc 4=2R 2A sin B sin C sin =AC B a sin 2sin sin 2=B C A b sin 2sin sin 2=C B A c sin 2sin sin 2=pr=))()((c p b p a p p ---(其中)(21c b a p ++=, r 为三角形内切圆半径)4.诱导公试注：奇变偶不变，符号看象限。

注：三角函数值等于α的同名三角函数值，前面加上一个把α看作锐角时，原三角函数值的符号；即：函数名不变，符号看象限注：三角函数值等于α的异名三角函数值，前面加上一个把α看作锐角时，原三角函数值的符号;即：函数名改变，符号看象限5.和差角公式①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos( =± ③βαβαβαtg tg tg tg tg ⋅±=± 1)( ④)1)((βαβαβαtg tg tg tg tg ⋅±=±6.二倍角公式：(含万能公式)①θθθθθ212cos sin 22sin tg tg +== ②θθθθθθθ22222211sin 211cos 2sin cos 2cos tg tg +-=-=-=-= ③θθθ2122tg tg tg -= ④22cos 11sin 222θθθθ-=+=tg tg ⑤22cos 1cos 2θθ+=7.半角公式：（符号的选择由2θ所在的象限确定） ①2cos 12sinθθ-±= ②2cos 12sin 2θθ-= ③2cos 12cos θθ+±= ④2cos 12cos 2θθ+=⑤2sin 2cos 12θθ=- ⑥2cos 2cos 12θθ=+ ⑦2sin2cos )2sin 2(cos sin 12θθθθθ±=±=±⑧θθθθθθθsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg8.积化和差公式：[])sin()sin(21cos sin βαβαβα-++=[])sin()sin(21sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++= ()[]βαβαβα--+-=cos )cos(21sin sin9.和差化积公式：①2cos2sin2sin sin βαβαβα-+=+ ②2sin2cos2sin sin βαβαβα-+=-③2cos2cos 2cos cos βαβαβα-+=+ ④2sin 2sin 2cos cos βαβαβα-+-=- 锐角三角形函数公式总结大全1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。