15克碳水化合物图示

碳水计算公式
碳水化合物是身体所需的三大营养素之一，也是能量来源之一。

在控制饮食的时候，计算碳水摄入量是非常重要的。

以下是一个碳水计算公式，可以帮助你掌握自己每天碳水化合物的摄入量。

碳水化合物摄入量 = （总热量×目标碳水化合物比例）÷每克碳水化合物的热量
总热量是指你需要消耗的每日总热量，目标碳水化合物比例是指你希望每天摄入的碳水化合物占总热量的比例。

每克碳水化合物的热量通常是4千卡（也有人使用4.2千卡）。

例如，如果一个人每天需要消耗2000千卡的热量，目标碳水化合物比例为50%，那么他每天应该摄入的碳水化合物量为（2000 ×0.5）÷ 4 = 250克。

当然，这个公式只是一个大概的指导，具体的碳水化合物摄入量还需根据个人的身体状况、活动水平和饮食习惯进行调整。

此外，也需要注意选择健康的碳水化合物来源，如全谷类食品、水果和蔬菜，而不是过多摄入加工食品、糖果和甜饮料等高糖食品。

- 1 -。

减肥的原理应用图示1. 为什么要减肥？•提升健康水平：减肥可以降低患心脏病、糖尿病和高血压等慢性疾病的风险。

•提升质量生活：减肥可以改善身体形象，增加自信心。

2. 减肥的原理减肥的原理是通过控制能量摄入和消耗的平衡来达到减轻体重的目的。

2.1 能量摄入•控制饮食：减少高热量的食物摄入，增加摄入低热量的蔬菜和水果。

•合理膳食结构：摄入适量的蛋白质、碳水化合物和脂肪，保证身体的正常运转。

2.2 能量消耗•运动：增加身体的活动量，包括有氧运动和力量训练。

•基础代谢：通过增加肌肉质量来提高基础代谢率，从而增加能量消耗。

3. 减肥的应用图示以下图示展示了减肥原理的应用过程：3.1 能量摄入控制•对高热量食物的控制：–减少高热量食物的摄入：•避免过多的糖分摄入：–控制糖果、巧克力等高糖食物的摄入量。

•减少油脂的摄入：–控制油炸食品、脂肪含量较高的肉类和乳制品的摄入量。

•限制碳水化合物的摄入：–减少米饭、面包等主食的摄入量。

–增加低热量食物的摄入：•增加蔬菜和水果的摄入量。

3.2 能量消耗增加•运动的应用：–有氧运动：•快走、跑步、骑车等有氧运动可以使身体产生消耗，加速脂肪燃烧。

–力量训练：•锻炼肌肉可以提高基础代谢率，增加能量消耗。

•基础代谢的应用：–提高肌肉含量：•进行针对性的力量训练，增加肌肉的含量。

4. 总结通过控制能量摄入和消耗的平衡，减肥的原理得以应用。

控制饮食、增加运动和提高基础代谢率是减肥的核心方法。

在减肥过程中，还要注意健康饮食和有规律的运动，以免对身体造成不良影响。

希望本文的图示能够帮助您更好地了解减肥的原理和应用方式。

一、选择题1．已知二元一次方程组2513377x yx y+=⎧⎨-=-⎩①②，用加减消元法解方程组正确的（）A．①×5-②×7B．①×2+②×3C．①×7－②×5D．①×3-②×2 2．如图，周长为78cm的长方形团由10个形状大小完全相同的小长方形拼成，其汇总一个小长方形的面积为（）A．232cm B．235cm C．236cm D．240cm3．若关于x、y的方程组228x yax y+=⎧⎨+=⎩的解为整数，则满足条件的所有a的值的和为（）A．6 B．9 C．12 D．164．若x，y均为正整数，且2x＋1·4y＝128，则x＋y的值为()A．3 B．5 C．4或5 D．3或4或55．下列四组数值中，方程组2534a b ca b ca b c++=⎧⎪-+=-⎨⎪--=-⎩的解是( )A．11abc=⎧⎪=⎨⎪=-⎩B．121abc=-⎧⎪=⎨⎪=-⎩C．112abc=-⎧⎪=⎨⎪=-⎩D．123abc=⎧⎪=-⎨⎪=⎩6．由方程组71x my m+⎧⎨-⎩＝＝可得出x与y的关系式是（）A．x+y=8 B．x+y=1 C．x+y=-1 D．x+y=-87．为了研究吸烟是否对肺癌有影响，某研究所随机地抽查了1000人．结果显示：在吸烟者中患肺癌的比例是2.5%，在不吸烟者中患肺癌的比例是0.5%，吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人．如果设这1000人中，吸烟者患肺癌的人数为x，不吸烟者患肺癌的人数为y，根据题意，下面列出的方程组正确的是（）A．2210002.5%0.5%x yx y-=⎧⎪⎨+=⎪⎩B．1000222.5%0.5%x yx y+=⎧⎪⎨-=⎪⎩C．10002.5%0.5%22x yx y-=⎧⎨+=⎩D．10002.5%0.5%22x yx y+=⎧⎨-=⎩8．某校体育器材室有篮球和足球共66个，其中篮球比足球的2倍多3个，设篮球有x 个，足球有y 个，根据题意可得方程组（ ）A ．x y 66 x 2y 3+=⎧⎨=-⎩ B ．x y 66x 2y 3+=⎧⎨=+⎩ C ．x y 66 y 2x 3+=⎧⎨=-⎩D ．x y 66 y 2x 3+=⎧⎨=+⎩9．如图，周长为34的矩形ABCD 被分成7个全等的矩形，则矩形ABCD 的面积为（ ）A ．280B ．140C ．70D ．19610．某校七年级1班学生为了参加学校文化评比买了22张彩色的卡纸制作如下图形（每个图形由两个三角形和一个圆形组成），已知一张彩色卡纸可以剪5个三角形，或3个圆形，要使圆形和三角形正好配套，需要剪三角形的卡纸有x 张，剪圆形的卡纸有y 张，可列式为（ ）A ．2256x y x y +=⎧⎨=⎩B ．2265x y x y +=⎧⎨=⎩C ．22310x y x y +=⎧⎨=⎩D ．22103x y x y +=⎧⎨=⎩11．下列各组值中，不是方程21x y -=的解的是（ ）A ．0,12x y =⎧⎪⎨=-⎪⎩B ．1,1x y =⎧⎨=⎩C ．1,0x y =⎧⎨=⎩D ．1,1x y =-⎧⎨=-⎩12．小月去买文具，打算买5支单价相同的签字笔和3本单价相同的笔记本，她与售货员的对话如下,那么一支笔和一本笔记本应付（ ）小月:您好,我要买5支签字笔和3本笔记本售货员:好的,那你应付款52元小月:刚才我把两种文具的单价弄反了,以为要付44元A ．10元B ．11元C ．12元D ．13元二、填空题13．若关于x ，y 的方程组4,44ax by cx dy -=⎧⎨+=⎩的解是8,4,x y =⎧⎨=⎩则关于x ，y 的方程组()()()()214,2144a x b y c x d y ⎧+--=⎪⎨++-=⎪⎩的解是______． 14．已知x ，y 满足方程组612328x y x y +=⎧⎨-=⎩，则x +y 的值为__．15．甲、乙两筐苹果各有若干千克，从甲筐拿出20%到乙筐后，又从乙筐拿出25%到甲筐，这时甲、乙两筐苹果的质量相等，则原来乙筐的苹果质量是甲筐的__________ % ． 16．若2(321)4330x y x y -++--=，则x y -=_____．17．已知012x y =⎧⎪⎨=-⎪⎩是方程组522x b y x a y -=⎧⎨+=⎩的解，则a b +的值为_______ ． 18．某超市促销活动，将车厘子、波罗蜜、山竹三种水果采用三种不同方式搭配成礼盒，分别是蒸蒸日上礼盒、独占鳌头礼盒、吉祥如意礼盒，将礼盒进行销售，每盒的总成本为盒中车厘子、波罗蜜、山竹三种水果成本之和，盒子成本忽略不计，蒸蒸日上每盒分别装有车厘子、波罗蜜、山竹三种水果8千克，4千克，3千克；独占鳌头每盒装有车厘子、波罗蜜、山竹三种水果3千克，8千克，6千克；蒸蒸日上每盒的总成本是每千克车厘子水果成本的14倍，每盒蒸蒸日上的销售利润是60%，每盒独占鳌头的售价是成本的43倍，每盒吉祥如意在成本上提高60%标价后打八折出售，获利为每千克车厘子水果成本的2.8倍，当销售蒸蒸日上、独占鳌头、吉祥如意三种礼盒的数量之比为5:2:5，则销售的总利润率为______．19．若方程组ax y c x by d -=⎧⎨-=⎩的解为12x y =⎧⎨=-⎩，则方程组y ax cby x d -=⎧⎨-=⎩的解为______．20．明代的程大位创作了《算法统宗》，它是一本通俗实用的数学书，将枯燥的数学问题化成了美妙的诗歌，读来朗朗上口，是将数字入诗的代表作．例如，其中有一首饮酒数学诗：“肆中饮客乱纷纷，薄酒名釂厚酒醇．醇酒一瓶醉三客，薄酒三瓶醉一人，共同饮了一十九，三十三客醉颜生．试问高明能算士，几多酶酒几多醇?”这首诗是说：“好酒一瓶，可以醉倒3位客人；薄酒三瓶，可以醉倒1位客人，如今33位客人醉倒了，他们总共饮下19瓶酒．试问其中好酒、薄酒分别是多少瓶?”请你根据题意，求出好酒是有_____瓶．三、解答题21．通过对一份中学生营养快餐的检测，得到以下信息：①快餐总质量为300g ；②快餐的成分：蛋白质、碳水化合物、脂肪、矿物质；③蛋白质和脂肪含量占50%；矿物质的含量是脂肪含量的2倍；蛋白质和碳水化合物含量占85%．（1）设其中蛋白质含量是(g)x ，脂肪含量是(g)y ，请用含x 或y 的代数式分别表示碳水化合物和矿物质的质量．（2）求每份营养午餐中蛋白质、碳水化合物、脂肪和矿物质的质量．22．元旦期间，甲、乙两个商场开展促销活动，甲商场实行“全场52折”的优惠；乙商场实行“满200元减100元”的优惠（如：某顾客购物320元，他需付款220元，购物420元，他也只需付款220元）．（1）张丽想买商场标价都是850元的同一套衣服，她应该选择哪家商场？（2）李明发现在甲、乙商场购买一样标价六百多元的某商品，最后付款额是一样的，请问此商品的标价是多少元？（3）丙商场推出“先打折”，再“满200元减100元”的活动．李明发现在丙商场购买（2）中的商品，虽然标价一样但比在乙商场要多付25元钱，问丙商场先打了多少折后再参加活动？23．对于平面直角坐标系xOy 中的点P (),a b 和图形W ，给出如下定义：如果图W 上存在一点Q (),c d 使得,,a c b d k =⎧⎨+=⎩，那么点P 是图形W 的“k 阶关联点” ()1若点P 是原点O 的“1-阶关联点”，则点P 的坐标为 ；()2如图，在ABC ∆中，()1,1A -，()2,4B --，()0,6C -．①若点P 是ABC ∆的“0阶关联点”，把所有符合题意的点P 都画在图中； ②若点P 是ABC ∆的“k 阶关联点”，且点P 在ABC ∆上，求k 的取值范围．24．已知α∠与β∠互为补角，且β∠比α∠的一半大15︒，求β∠的余角．25．解方程组（1）()() 322 3553x yx y⎧-=+⎪⎨+=-⎪⎩．（2）1 32321x yx y⎧-=-⎪⎨⎪-=⎩．26．阅读小林同学数学作业本上的截图内容并完成任务．任务：（1）这种解方程组的方法称为________；（2）小林的解法正确吗？________（填“正确”或“不正确”），如果不正确，错在第________步，并选择恰当的方法解该方程组．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】方程组利用加减消元法变形，判断即可．【详解】解：用加减消元法解方程组2513377x yx y+=⎧⎨-=-⎩①②，用①×3-②×2可以消去x，选项A，B， C无法消去方程组中的未知数，故选：D．【点睛】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法和加减消元法．2．C解析：C【分析】设小长方形的长为x ，宽为y ，列出二元一次方程组并求解，即可得出结论． 【详解】解：设小长方形的长为x ，宽为y ，根据图形可得： 45678x yx y =⎧⎨+=⎩， 解得123x y =⎧⎨=⎩，∴一个小长方形的面积为212336cm ⨯=， 故选：C ． 【点睛】本题考查二元一次方程组的实际应用，根据图形找出等量关系是解题的关键．3．C解析：C 【分析】先把a 看作已知数求出42x a =-，然后结合方程组的解为整数即可求出a 的值，进而可得答案． 【详解】解：对方程组2{28x y ax y +=+=①②， ②－①×2，得()24a x -=，∴42x a =-， ∵关于x 、y 的方程组228x y ax y +=⎧⎨+=⎩的解为整数，∴21,2,4a -=±±±，即a =﹣2、0、1、3、4、6，∴满足条件的所有a 的值的和为﹣2+0+1+3+4+6=12． 故选：C ． 【点睛】本题考查了二元一次方程组的解法，正确理解题意、熟练掌握解二元一次方程组的方法是解题关键．4．C解析：C 【解析】∵2x ＋1·4y ＝128，27＝128， ∴x ＋1＋2y ＝7，即x ＋2y ＝6. ∵x ，y 均为正整数， ∴22x y =⎧⎨=⎩或41x y =⎧⎨=⎩∴x ＋y ＝4或5.5．B解析：B 【解析】分析：首先利用②－①和②+③得出关于a 和b 的二元一次方程组，从而求出a 和b 的值，然后将a 和b 代入任何一个式子得出c 的值，从而得出方程组的解．详解：0?25?34? a b c a b c a b c ++=⎧⎪-+=-⎨⎪--=-⎩①②③，②－①可得：a －2b=－5 ④， ②+③可得：5a －2b=－9 ⑤，④－⑤可得：－4a=4，解得：a=－1， 将a=－1代入④可得：b=2，将a=－1，b=2代入①可得：c=－1，∴方程组的解为：121a b c =-⎧⎪=⎨⎪=-⎩，故选B ．点睛：本题主要考查的是三元一次方程组的解法，属于基础题型．消元法的使用是解决这个问题的关键．6．A解析：A 【分析】将第二个方程代入第一个方程消去m 即可得． 【详解】71x m y m +⎧⎨-⎩＝①＝②，将②代入①，得：x+y-1=7，则x+y=8，故选A ． 【点睛】本题考查了解一元一次方程和二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．7．A解析：A 【分析】根据在“吸烟者中患肺癌的比例是2.5%，在不吸烟者中患肺癌的比例是0.5%，吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人”即可解答． 【详解】 解：由题意可得，22+10002.5%0.5%x y xy -=⎧⎪⎨=⎪⎩， 故选：A ．【点睛】本题主要考查是二元一次方程的应用，正确的理解题意，列出方程是解题的关键．8．B解析：B【分析】根据题中的等量关系列方程组即可【详解】解：依题意，得：x y66 x2y3+=⎧⎨=+⎩．故选：B．【点睛】本题考查了由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键．9．C解析：C【解析】解：设小长方形的长、宽分别为x、y，依题意得：，解得：，则矩形ABCD的面积为7×2×5=70．故选C．【点评】考查了二元一次方程组的应用，此题是一个信息题目，首先会根据图示找到所需要的数量关系，然后利用这些关系列出方程组解决问题．10．A解析：A【分析】设需要剪三角形的卡纸有x张，剪圆形的卡纸有y张，根据彩色卡纸的总张数为22张其剪出三角形的数量为圆的2倍，即可得出关于x、y的二元一次方程组，此题得解．【详解】设需要剪三角形的卡纸有x张，剪圆形的卡纸有y张，根据题意得：22 56x yx y+=⎧⎨=⎩．故选：A．【点睛】此题考查由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键．11．B解析：B 【分析】将x 、y 的值分别代入x-2y 中，看结果是否等于1，判断x 、y 的值是否为方程x-2y=1的解． 【详解】 A 项，当0x =，12y 时，1202()12x y -=-⨯-=，所以0,12x y =⎧⎪⎨=-⎪⎩是方程21x y -=的解；B 项，当1x =，1y =时，21211y =-⨯=-，所以1,1x y =⎧⎨=⎩不是方程21x y -=的解； C 项，当1x =，0y =时，21201x y -=-⨯=，所以1,0x y =⎧⎨=⎩是方程21x y -=的解； D 项，当1x =-，1y =-时，212(1)1x y -=--⨯-=，所以1,1x y =-⎧⎨=-⎩是方程21x y -=的解， 故选B. 【点睛】本题考查二元一次方程的解的定义，要求理解什么是二元一次方程的解，并会把x ，y 的值代入原方程验证二元一次方程的解．12．C解析：C 【分析】设购买1支签字笔应付x 元，1本笔记本应付y 元，根据题意可得5x+3y=52和3x+5y=44，进而求出x+y 的值． 【详解】设购买1支签字笔应付x 元，1本笔记本应付y 元，根据题意得53523544x y x y +⎧⎨+⎩＝＝，解得8x+8y=96， 即x+y=12，所以在单价没有弄反的情况下，购买1支签字笔和1本笔记本应付12元， 故选C ． 【点睛】本题考查了二元一次方程组的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程组求解．二、填空题13．【分析】利用已知方程组的解和换元法求解即可；【详解】设则原方程组可化为∵关于的方程组的解是∴∴即∴关于的方程组的解是；故答案是【点睛】本题主要考查了二元一次方程组的求解准确分析计算是解题的关键解析：65x y =⎧⎨=⎩【分析】利用已知方程组的解和换元法求解即可； 【详解】设2x m +=，1y n -=， 则原方程组可化为4,44am bn cm dn -=⎧⎨+=⎩，∵关于x ，y 的方程组4,44ax by cx dy -=⎧⎨+=⎩的解是84x y =⎧⎨=⎩，∴84m n =⎧⎨=⎩， ∴2814x y +=⎧⎨-=⎩，即65x y =⎧⎨=⎩，∴关于x ，y 的方程组()()()()214,2144a x b y c x d y ⎧+--=⎪⎨++-=⎪⎩的解是65x y =⎧⎨=⎩；故答案是65x y =⎧⎨=⎩．【点睛】本题主要考查了二元一次方程组的求解，准确分析计算是解题的关键．14．5【分析】根据两个方程系数的关系将两个方程相加即可得到答案【详解】解：①+②得：4x+4y ＝20则x+y ＝5故答案为：5【点睛】此题考查解二元一次方程组—特殊法根据所求的式子中各系数与方程组的关系将解析：5 【分析】根据两个方程系数的关系将两个方程相加即可得到答案． 【详解】解：612328x y x y +=⎧⎨-=⎩①②，①+②得：4x +4y ＝20， 则x +y ＝5， 故答案为：5．【点睛】此题考查解二元一次方程组—特殊法，根据所求的式子中各系数与方程组的关系，将原方程组对应相加或相减即可得到答案的方法更为简便．15．140【分析】设甲乙两筐苹果各有先求出从甲筐拿出20到乙筐后甲乙两筐分别为再求出从乙筐拿出25到甲筐后甲乙两筐分别为：列方程求出x 与y 的关系即可【详解】设甲乙两筐苹果各有从甲筐拿出20到乙筐后甲乙两解析：140【分析】设甲、乙两筐苹果各有x 、kg y ，先求出从甲筐拿出20%到乙筐后，甲、乙两筐分别为80%x ，20%y x +，再求出从乙筐拿出25%到甲筐后，甲、乙两筐分别为：171204x y +，33420y x +，列方程17133204420x y y x +=+，求出x 与y 的关系即可． 【详解】设甲、乙两筐苹果各有x 、kg y ，从甲筐拿出20%到乙筐后，甲、乙两筐分别为80%x ，20%y x +，从乙筐拿出25%到甲筐后，甲、乙两筐分别为：()17180%25%20%204x y x x y +⨯+=+， ()3375%20%420y x y x ⨯+=+， 由题可得：17133204420x y y x +=+， 解得75y x =， 75y x =， 则原来乙筐苹果质量为甲筐的：7100%100%140%5y x ⨯=⨯=． 故答案为：140．【点睛】本题考查循环倒液类型问题，掌握循环倒液类型问题的解法，抓住经过两次循环两者质量相等构造等式（或方程）解决问题是关键． 16．4【分析】根据非负数的性质两个非负数相加和为0这两个非负数的值都为0解出xy 的值再代入原式中即可【详解】解：∵∴①×3-②×2得把代入①得解得∴故答案为：4【点睛】本题考查了非负数的性质及二元一次方解析：4【分析】根据非负数的性质“两个非负数相加，和为0，这两个非负数的值都为0”解出x 、y 的值，再代入原式中即可．【详解】解：∵2(321)4330x y x y -++--=，∴32104330x y x y -+=⎧⎨--=⎩①②， ①×3-②×2得，9x =-，把9x =-代入①得，27210y --+=，解得13y =-，∴9134x y -=-+=．故答案为：4．【点睛】本题考查了非负数的性质及二元一次方程组的解法．注意：几个非负数的和为零，则每一个数都为零．17．【分析】将代入方程组求出a 和b 的值即可求解【详解】将代入方程组得：解得：∴故答案为：【点睛】本题考查了二元一次方程组的解方程组的解即为能使方程组中两方程都成立的未知数的值解析：0【分析】 将012x y =⎧⎪⎨=-⎪⎩代入方程组522x b y x a y -=⎧⎨+=⎩，求出a 和b 的值，即可求解． 【详解】 将012x y =⎧⎪⎨=-⎪⎩代入方程组522x b y x a y -=⎧⎨+=⎩，得： 121222b a ⎧-=-⎪⎪⎨⎛⎫⎪=⨯- ⎪⎪⎝⎭⎩， 解得：1212a b ⎧=-⎪⎪⎨⎪=⎪⎩， ∴11022a b +=-+=． 故答案为：0．【点睛】本题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．18．44【分析】分别设每千克车厘子菠萝蜜山竹三种水果的成本价分别为xyz 再由题意分别求出每一种礼盒的成本利润则可求解【详解】设设每千克车厘子菠萝蜜山竹三种水果的成本价分别为xyz 由题意可得：∴蒸蒸日上的解析：44%【分析】分别设每千克车厘子、菠萝蜜、山竹三种水果的成本价分别为x 、y 、z ，再由题意分别求出每一种礼盒的成本、利润则可求解．【详解】设设每千克车厘子、菠萝蜜、山竹三种水果的成本价分别为x 、y 、z ，由题意可得：84314x y z x ++=∴436y z x +=蒸蒸日上的总成本为：84314x y z x ++=， 每盒的利润是：342(843)55x y z x ++=； 独占鳌头的总成本为：38632615x y z x x x ++=+⨯=， 每盒的售价是：4(386)3x y z ++， 每盒的利润是：()()41(386)386386533x y z x y z x y z x ++-++=++= 每盒吉祥如意的销售利润是2.8x ，则成本为：()2.810160%80%1x x =+⨯-， 当销售蒸蒸日上、独占鳌头、吉祥如意三种礼盒的数量之比为5:2:5，总成本是：51425510150x x x x ⨯+⨯+⨯=， 总利润是：425255 2.8665x x x x ⨯+⨯+⨯= ∴总利润是6644%150x x= 故答案为：44%【点睛】本题考查了三元一次方程的应用；理解题意，能够通过所给的量之间的关系列出正确的方程是解题的关键．19．【分析】用换元法求解即可【详解】解：∵∴∵方程组的解为∴∴故答案为：【点睛】此题考查利用换元法解二元一次方程组注意要根据方程的特点灵活选用合适的方法解数学题时把某个式子看成一个整体用一个变量去代替它解析：12x y =-⎧⎨=⎩【分析】用换元法求解即可．【详解】解：∵y ax c by x d -=⎧⎨-=⎩， ∴()()()()a x y c x b y d ⎧---=⎪⎨---=⎪⎩， ∵方程组ax y c x by d -=⎧⎨-=⎩的解为12x y =⎧⎨=-⎩， ∴12x y -=⎧⎨-=-⎩， ∴12x y =-⎧⎨=⎩， 故答案为：12x y =-⎧⎨=⎩． 【点睛】此题考查利用换元法解二元一次方程组，注意要根据方程的特点灵活选用合适的方法． 解数学题时，把某个式子看成一个整体，用一个变量去代替它，从而使问题得到简化，这叫换元法．20．10【分析】根据好酒数量+薄酒数量=19和喝好酒醉倒人数+喝薄酒醉倒人数=33可列方程组解之即可【详解】解：设有好酒x 瓶薄酒y 瓶根据题意可列方程组为解得：∴好酒是有10瓶故答案为：10【点睛】本题主解析：10【分析】根据“好酒数量+薄酒数量=19和喝好酒醉倒人数+喝薄酒醉倒人数=33”可列方程组，解之即可．【详解】解：设有好酒x 瓶，薄酒y 瓶．根据题意，可列方程组为193333x y y x +=⎧⎪⎨+=⎪⎩，解得：109x y =⎧⎨=⎩， ∴好酒是有10瓶，故答案为：10．【点睛】本题主要考查由实际问题抽象出二元一次方程组，解题的关键是掌握理解题意，找到题目蕴含的相等关系．三、解答题21．（1）碳水化合物：255-x ；矿物质：2y ；（2）蛋白质质量为135g ，碳水化合物质量为120g ，脂肪质量为15g ，矿物质质量为30g【分析】（1）根据“矿物质的含量是脂肪含量的2倍，蛋白质和碳水化合物含量占85%”解答； （2）由题意得等量关系：蛋白质的质量+脂肪的质量=300×50%，四种成分含量之和=300，列出方程组，再解即可．【详解】解：（1）由题可知，矿物质的质量为2y （g ）．碳水化合物的质量为300×85%-x=255-x （g ）．（2）由题意可得：30050%2552300x y x y x y +=⨯⎧⎨-+++=⎩，解得13515x y =⎧⎨=⎩， ∴蛋白质质量为135g ，碳水化合物质量为255-135=120g ，脂肪质量为15g ，矿物质质量为2×15=30g ．【点睛】此题主要考查了二元一次方程组的应用，关键是正确理解题意，找出题目中的等量关系，表示出碳水化合物的质量，矿物质的质量，脂肪的含量，蛋白质的质量，再列方程． 22．（1）甲；（2）625；（3）丙商场先打了8.8折后再参加活动．【分析】（1）分别计算在甲，乙商场的费用，比较后可得答案；（2）设商品的标价为x 元，判断：600＜x ＜800，再根据最后付款额是一样的列方程，解方程可得答案；（3）先求解同种商品在丙商场付款350元，设丙商场先打y 折，再“满200元减100元”，且设减了n 个100，可得方程625100350,10y n ⨯-= 由n 为正整数，进行讨论并检验，从而得到答案．【详解】解：（1）张丽在甲商场购买所花：85052%442⨯=（元），在乙商场购买所花：8504100450-⨯=（元），由442＜450，张丽应该选择甲商场购买．（2）设商品的标价为x 元，由题意可得：600＜x ＜800，则 52%3100,x x =-⨯0.48300,x ∴=625x ∴=答：此商品的标价是625元．（3）由（2）得：625元的商品在乙商场付款6253100325-⨯=元，所以同种商品在丙商场付款325+25=350元，设丙商场先打y 折，再“满200元减100元”，且设减了n 个100，则 625100350,10y n ⨯-= 整理得：5828,y n -=8528,n y ∴=-5288y n -∴= ， 又n 为正整数，当5288y -=时，7.2,1,y n == 经检验：7.2625=45010⨯元，此时2n =，不合题意，舍去， 当52816y -=时，8.8,2,y n == 经检验：8.862555010⨯=元，此时2n =，符合题意， 当52824y -=时，10.4,y = 此时不符合题意，故舍去， 综上：丙商场先打了8.8折后再参加活动．【点睛】本题考查的是一元一次方程的应用，二元一次方程的正整数解的应用，分类讨论的数学思想，掌握以上知识是解题的关键．23．（1）()0,1-；（2）①见解析；②122k -≤≤-【分析】（1）根据“k 阶联点”的公式代入数值计算即可；（2）①根据公式求出点P 分别是点A 、B 、C 的“0阶关联点”时的坐标，画出三点构成的图形即可；②由公式可知：点P 是某点的 “k 阶关联点”时，两点的横坐标相同，设点P 的坐标为（m ，n ），由点P 分别是点A 、B 、C 的“k 阶关联点”时得到点P 的坐标，即可求出k 值，由此得到答案．【详解】（1）设点P 的坐标为（k ，c ），由题意得01k c =⎧⎨=-⎩， ∴点P 的坐标为（0，-1），故答案为：（0，-1）；（2）设点P 的坐标为（a ，b ），①若点P 是点A （1，-1）的“0阶关联点”，∴110a b =⎧⎨-=⎩，解得11a b =⎧⎨=⎩， ∴P 1（1,1）；若点P 是点B （-2，-4）的“0阶关联点”，∴240a b =-⎧⎨-=⎩，解得24a b =-⎧⎨=⎩， ∴P 2（-2,4）；若点P 是点C （0，-6）的“0阶关联点”，∴060a b =⎧⎨-=⎩，解得06a b =⎧⎨=⎩， ∴P 3（0,6）；故点P 的坐标为P 1（1,1）或P 2（-2,4）或P 3（0,6）；则△P 1P 2P 3是所求P 点的图形.②由公式可知：点P 是某点的 “k 阶关联点”时，两点的横坐标相同，设点P 的坐标为（m ，n ），∵点P 在ABC ∆上，∴当点P 是点()1,1A -的 “k 阶关联点”，则点P 的坐标为（1，-1）∴k =-1-1=-2，若2k >-，则根据题意有1n >-，即P 的纵坐标大于-1，此时无法满足P 在ABC ∆上； 当点P 是()2,4B --的 “k 阶关联点”，则点P 的坐标为（-2，-4），∴k =-4-4=-8，当点P 是()0,6C -的 “k 阶关联点”，则点P 的坐标为（0，-6），∴k =-6-6=-12，若12k <-，则根据题意有6n <-，即P 的纵坐标小于-6，此时无法满足P 在ABC ∆上； ∴综上所述，k 的取值范围122k -≤≤-．【点睛】此题考查点与坐标，新定义坐标，二元一次方程组的应用，正确理解新定义列得方程求解坐标是解题的关键．24．20°．【分析】根据补角的概念和题意列出二元一次方程组，解方程组求出∠α的值，根据余角的概念计算即可．【详解】 解：由题意得，1801152αββα∠+∠︒⎧⎪⎨∠-∠︒⎪⎩＝＝ ， 解得11070αβ∠︒⎧⎨∠︒⎩＝＝， 90°-β∠=20°．答：β∠的余角为20°．【点睛】本题考查的是余角和补角的概念，若两个角的和为90°，则这两个角互余；若两个角的和等于180°，则这两个角互补．同时还考查了解二元一次方程组．25．（1）57x y =⎧⎨=⎩；（2）34x y =⎧⎨=⎩． 【分析】（1）先将两个方程分别整理，再利用加减法解方程组；（2）先将方程①化简，再利用加减法解方程组．【详解】（1）3(2)2355(3)x y x y -=+⎧⎨+=-⎩①②， 整理得38x y -=③，3520x y -=-④，③-④，得7y =，将7y =代入③，得5x =，所以原方程的解是57x y =⎧⎨=⎩． （2）132321x y x y ⎧-=-⎪⎨⎪-=⎩①②，由①整理得236x y -=-③，23⨯-⨯②③，得4y =，将4y =代入②，得3x =，所以原方程的解是34x y =⎧⎨=⎩． 【点睛】此题考查解二元一次方程组，掌握解二元一次方程组的方法：代入法、加减法，根据二元一次方程组的特点选用恰当的解法是解题的关键．26．（1）代入消元法；（2）不正确，二，39x y =-⎧⎨=-⎩【分析】（1）由解二元一次方程的的方法，即可得到答案；（2）由代入消元法的步骤进行计算，即可得到答案．【详解】解：()1这种解方程组的方法叫代入消元法．故答案为：代入消元法．()2小林的解法不正确，错在第二步，正确解法：由①得，23y x =-③，把③代入②得，(23)12x x +-=-，解得：3x =-，把3x =-代入③，解得：9y =-；则方程组的解为：39.x y =-⎧⎨=-⎩， 【点睛】本题考查了解二元一次方程组的方法，解题的关键是熟练掌握解二元一次方程组的方法进行解题．。

2023-2024学年江苏省扬州市江都区第三中学九年级下学期3月阶段检测化学试题1.“一带一路”是丝绸之路经济带和21世纪海上丝绸之路的简称，是合作发展的理念和倡议。

下列古代生产工艺中主要体现物理变化的是A．纺纱织布B．烧制瓷器C．粮食酿酒D．冶炼生铁2.下列物质由离子构成的是A．氮气B．氯化钠C．二氧化碳D．金刚石3.下图是表示物质分子的示意图，图中“”和“”分别表示两种含有不同质子数的原子，则图中表示单质的是A．B．C．D．4.化学元素与人体健康息息相关。

下列关于元素影响人体健康的说法不正确的是A．缺氟易产生龋齿B．缺硒会引起甲状腺肿大C．老年人缺钙会导致骨质疏松D．儿童缺锌会影响发育5.小强发现自家农田中的水稻叶子发黄且茎杆细弱，小强建议父亲施用含钾的复合肥料。

下列肥料符合要求的是A．（NH 4）2 SO 4B．KNO 3C．（NH 4）2HPO 4D．K 2 CO 36.我国在国之重器的研发中取得了瞩目成就，下列“重器”所用材料为无机非金属材料的是A．歼 20 战斗机中的玻璃钢雷达罩B．山东舰航母使用的碳纤维复合材料C．C919 大飞机机身使用铝锂合金D．奋斗者号潜水器中的空心玻璃微球7.下列图示的实验操作中，正确的是A．浓硫酸的稀释B．称量NaOH固体C．点燃酒精灯D．闻气体气味8.下列有关物质的性质与用途具有对应关系的A．氮气化学性质稳定，可用于霓虹灯B．石墨有导电性，可用于生产铅笔芯C．活性炭有吸附性，可用作除味剂D．氢氧化钠有吸水性，可作食品干燥剂9.我国北斗导航卫星系统采用铷原子钟提供精确时间，铷元素在元素周期表中的相关信息与铷原子的原子结构示意图如图所示。

下列说法不正确的是A．m的值是37，n的值是1 B．铷元素属于金属元素C．氯化铷的化学式为RbCl 2D．铷的相对原子质量为85.4710.下列实验方案不能达到实验目的的是A．用碘水检验米汤中是否含有淀粉B．用酚酞检验食盐水和石灰水C．用加热法除去K 2 MnO 4中的KMnO 4D．用灼烧法区分聚乙烯和聚氯乙烯11.某化学兴趣小组在老师的指导下，设计了如图实验验证可燃物燃烧的条件，说法不正确的是A．步骤Ⅱ白磷燃烧产生大量白烟B．步骤Ⅰ、Ⅱ红磷对比说明燃烧需要氧气C．该实验可以推测出白磷着火点比红磷低D．在密闭装置中进行实验可减少环境污染12.清华大学研究人员成功研制出一种纳米纤维催化剂，可将二氧化碳转化成液体燃料甲醇，其微观示意图如下（图中的微粒恰好完全反应）。

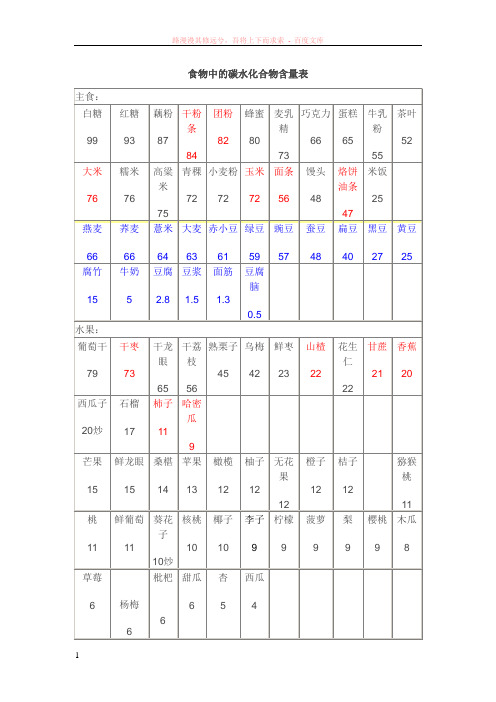
食物中的碳水化合物含量表主食：白糖99 红糖93藕粉87干粉条84团粉82蜂蜜80麦乳精73巧克力66蛋糕65牛乳粉55茶叶52大米76糯米76高粱米75青稞72小麦粉72玉米72面条56馒头48烙饼油条47米饭25燕麦66 荞麦66薏米64大麦63赤小豆61绿豆59豌豆57蚕豆48扁豆40黑豆27黄豆25腐竹15 牛奶5豆腐2.8豆浆1.5面筋1.3豆腐脑0.5水果：葡萄干79 干枣73干龙眼65干荔枝56熟栗子45乌梅42鲜枣23山楂22花生仁22甘蔗21香蕉20西瓜子20炒石榴17柿子11哈密瓜9芒果15 鲜龙眼15桑椹14苹果13橄榄12柚子12无花果12橙子12桔子12猕猴桃11桃11 鲜葡萄11葵花子10炒核桃10椰子10李子9柠檬9菠萝9梨9樱桃9木瓜8草莓6 杨梅6 枇杷6甜瓜6杏5西瓜4蔬菜：银耳78 平菇70木耳66黄花菜60干冬菇60香菇59海带56紫菜49猴头菇45黑木耳34地瓜30 百合29海藻29慈菇26大蒜24山芋22荸荠21藕20蚕豆芽20土豆17莲子16干山药14 黄花菜12鲜芋头12蒜苗10姜9胡萝卜8洋葱8黄豆芽7香菜7水萝卜7毛豆7大葱6 马兰6冬笋6甜菜6四季豆6白萝卜6丝瓜5茭白5辣椒5青尖芥菜5菜豆5空心菜5 苋菜5春菜4刀豆4菜花4小葱4柿子椒4青绿豆芽4圆白菜3芥蓝3韭菜3韭黄3 生菜3莴笋叶3龙须菜3芦笋苤蓝3卷心菜3菠菜3茄子3苦瓜3雪里红3黄瓜3冬瓜2 芹菜2番茄2蘑菇2油菜2大白菜2小白菜2莴笋2南瓜1松蘑0.4含糖量 食物含糖量 食物1％ 南瓜、紫菜、生菜2%菠菜、芹菜、小白菜、小青菜、西红柿、冬瓜、黄瓜3%大白菜、青菜心、韭黄、豌豆苗、茄子、酸菜、豆腐4％ 绿豆芽、油菜、韭菜、春笋、茭白、花菜、空心菜、西瓜、扁豆 5％ 小葱、青蒜、辣椒、丝瓜、韭菜花、酱豆腐6% 白罗卜、冬笋、黄豆芽、豆腐干、桃、枇杷、豆牙7－8%香菜、毛豆、黄胡罗卜、红胡罗卜、葱头、樱桃、柠檬9－10％ 榨菜、蒜苗、杏子、葡萄、柚子、豆腐皮11－12％ 柿子、沙果、桔子、梨、橄榄、豌豆 14－17％ 荔枝、山药、苹果、土豆、石榴、西瓜子膳食中缺乏碳水化合物将导致全身无力，疲乏、血糖含量降低，产生头晕、心悸、脑功能障碍等。

高糖（碳水化合物）食物碳水化合物是机体能量的主要来源，特别是提供唯一可被脑细胞及红血球所需的能量。

不被使用的葡萄糖，可变成脂肪储存在体内。

碳水化合物中含有一些不被消化的纤维，它有吸水及吸脂作用，所以有助清洗大肠及降低胆固醇，令大便畅通、体内废物顺利排出体外（见膳食纤维节）。

碳水化合物主要可分为糖、寡糖和多糖。

糖主要存在于精制糖类中（如：蔗糖、蜜糖、糖果等）、蔬菜以至奶类制品。

多糖则主要存在于淀粉类食物中，例如谷类、面包、土豆等。

高含量碳水化合物的食物很多，除了纯品（如糖类和淀粉）大约含量在90%～100%之外，碳水化合物含量高的食物主要是谷类（如面粉、大米、玉米等）和薯类（如白薯、土豆等）谷类食物一般含碳水化合物60%～80%；薯类脱水后高达80%左右；豆类为40%～60%。

它们是血糖的主要来源。

我国营养学会建议，碳水化合物摄入量占总能量的55%左右，相当于一天摄入300g～500g的谷类食物。

表1—13 高碳水化合物食物含量表（以100g可食部计）食物名称含量g 食物名称含量g白砂糖 99.9 麦芽糖 82.0冰糖 99.3 无核蜜枣 81.9什绵糖 98.9 脱水洋葱（白） 81.9绵白糖 98.9 籼米粉 81.5酸梅晶 98.4 枣（干） 81.1水晶糖 98.2 白薯粉 80.9固体桔子饮料 97.5 脱水马铃薯 80.7宝宝福 97.3 脱水洋葱（紫） 80.6猕猴桃晶 97.1 白薯干 80.5红塘 96.6 糜子米（炒） 80.5桔子晶 96.5 牛奶饼干 80.3山查晶 95.9 香油炒面 80.1豌豆粉丝 91.7 芡食米 79.6泡泡糖 89.8 南瓜粉 79.5麻香糕 88.7 脱水百合 79.3麻烘糕 87.2 陈皮 79.0米花糖 85.8 五谷香 78.9团粉/淀粉85.8—85.3 魔芋精粉 78.8龙虾片 85.5 栗子（干） 78.4苹果脯 84.9 红果（干） 78.4奶糖 84.5 籼米 78.3蜜枣 84.4 糯米（平均） 78.3茯苓夹饼 84.3 江米条 78.1豆腐粉 84.3 脱水胡萝卜 77.9粉条 84.2 稻米（平均） 77.9粉丝 83.7 小米面 77.7葡萄干 83.4 干切面 77.7南瓜果脯 83.3 桃脯 77.6 杏干 83.2 西瓜脯/青梅果脯 77.5 玉米片（即食） 82.3 马铃薯粉 77.4 杏脯 82.0 麦乳精 77.0。

碳水化合物含量表
食品名称：苹果
每份的重量或体积：1个中等大小的苹果
每份的碳水化合物含量：15.3克
食品的总碳水化合物含量：15.3克
碳水化合物的类型：简单碳水化合物
食品的糖分含量：10.7克
其他重要营养素含量：每份含有约0.5克蛋白质，0.2克脂肪，2.8克纤维
食品的热量含量：约62千卡
碳水化合物来源：水果
食品的升糖指数（GI值）：36
食品名称：燕麦片
每份的重量或体积：1/2杯
每份的碳水化合物含量：7.8克
食品的总碳水化合物含量：7.8克
碳水化合物的类型：复杂碳水化合物
食品的糖分含量：0.5克
其他重要营养素含量：每份含有约2.8克蛋白质，1.9克脂肪，2.9克纤维
食品的热量含量：约114千卡
碳水化合物来源：谷物
食品的升糖指数（GI值）：55
请注意，这只是一份示例表格，实际数据可能因食品品牌、生产批次和规格而有所不同。

建议在购买食品后仔细查看食品标签以获取准确信息。

28.3 表示一组数据平均水平的量（2）[中位数、众数和截尾平均数]第一组28-71、一个学习小组共有10人，20岁的4人，18岁的2人，21岁的2人，17岁的1人，25岁的1人，下列判断正确的有（）个。

①小组成员的平均年龄是20.2岁；②小组成员的平均年龄是20岁；③小组成员年龄的中位数是20岁；④小组成员年龄的中位数是20.5岁A、0B、1C、2D、32、把97个数据从小到大排列，中位数是第个数据。

3、若1、2、3、a的平均数为5，则a的值是。

4、数据0.5，0.8，0.9，1.0的中位数是。

，平均数是。

6、某班组织一次数学测试，全班学生成绩的分布情况如图28-7-1：某班数学成绩统计图全班学生数学成绩的众数是分，全班学生数学成绩为众数的有人，全班学生成绩的中位数是分。

学生数O图 28 - 7 - 17、在一场演唱比赛中，十位评委给一名歌手的演唱打分如下：9.73，9.66，9.83，9.89，9.76，9.86，9.79，9.85，9.68，9.74.若去掉一个最高分和一个最低分，求这名歌手的最后得分（截尾平均数）。

8、贵阳市某中学开展“八荣八耻”为主题的社会主义荣辱观教育活动，举办了讲演、书法、作文、手抄报、小品、漫画六项比赛（每个同学限报一项），学生参加情况如下表：认真观察阅读统计表后，回答下列问题： （1）请补充完成这个统计表；（2）本次参加比赛的总人数是人，本次比赛项目的众数是 ；（3）手抄报作品与漫画作品的获得人数分别是6人和3人，你认为“手抄报作品比漫画作品的获奖率高”这种说法是否正确。

9、小红的爸爸为了了解小红这学期在家看电视时间，随机挑选了某个星期对小红进行观察，并记录了她看电视的时间（分）： （1）请分别计算小红这周内在家看电视时间的平均数和中位数；（2）你认为应选中位数平均数中哪一个表示小红这一周在家看电视的时间更好？为什么？ （3）你认为能否用（2）的数据表示本学期小红在家看电视的一般时间？为什么？10、某初二年级320名学生在进行电脑培训的前后各参加一次水平相同的考试，考分都以统一标准划分成“不合格”、“合格”、“优秀”三个等级，为了了解电脑培训的效果，用抽签方式得到其中32名学生的两次考试考分等级，所绘制的统计图如图28-7-2所示。