Entanglement Entropy beyond the Free Case

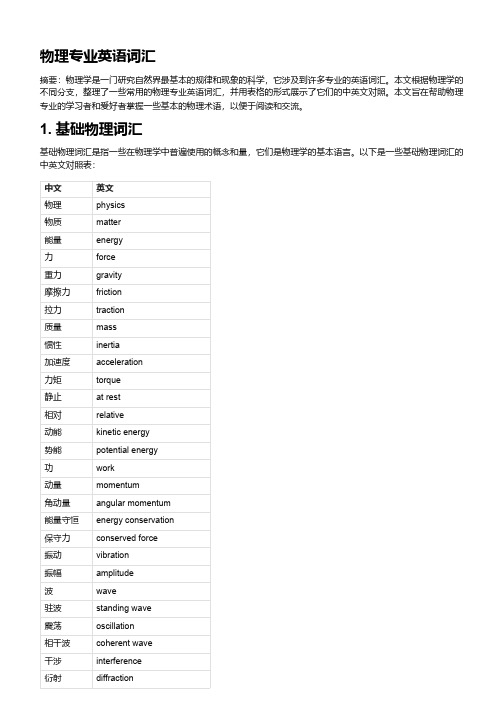
物理专业英语词汇摘要：物理学是一门研究自然界最基本的规律和现象的科学，它涉及到许多专业的英语词汇。

本文根据物理学的不同分支，整理了一些常用的物理专业英语词汇，并用表格的形式展示了它们的中英文对照。

本文旨在帮助物理专业的学习者和爱好者掌握一些基本的物理术语，以便于阅读和交流。

1. 基础物理词汇基础物理词汇是指一些在物理学中普遍使用的概念和量，它们是物理学的基本语言。

以下是一些基础物理词汇的中英文对照表：中文英文物理physics物质matter能量energy力force重力gravity摩擦力friction拉力traction质量mass惯性inertia加速度acceleration力矩torque静止at rest相对relative动能kinetic energy势能potential energy功work动量momentum角动量angular momentum能量守恒energy conservation保守力conserved force振动vibration振幅amplitude波wave驻波standing wave震荡oscillation相干波coherent wave干涉interference衍射diffraction轨道orbit速度velocity速率speed大小magnitude方向direction水平horizontal竖直vertical相互垂直perpendicular坐标coordinate直角坐标系Cartesian coordinate system极坐标系polar coordinate system2. 电学和磁学词汇电学和磁学是研究电荷、电流、电场、磁场等现象和规律的物理学分支，它们与光学、热学、原子物理等有着密切的联系。

以下是一些电学和磁学词汇的中英文对照表：中文英文电子electron电荷charge电流current电场electric field电通量electric flux电势electric potential导体conductor电介质dielectric绝缘体insulator电阻resistor电阻率resistivity电容capacitor3. 物理专业英语词汇物理专业英语词汇是指在物理学的学习和研究中经常使用的一些专业术语，它们涵盖了物理学的各个分支和领域，如力学、电磁学、光学、热学、量子力学等。

山西大同大学教学名师 — — 赵 仁姓 名赵 仁 性 别男 民 族汉族 职 称 教授 职 务处长 出生年月 1956.11 政治面貌群 众毕业学校 西安交大学 位 博 士 学 历博士研究生参加工作时间1981.09教学及科研成果简介赵 仁 ，1956年11月生于山西朔州，联系地址：山西大同大学研究生处，大同，037009 Email：zhaoren2969@； zhao2969@一、教育科研经历学历教育2004.09 — 2007.12：西安交通大学攻读博士学位，理学博士1995.09 — 1997.07：山西教育学院物理系1978.09 — 1981.07：雁北师范专科学校物理系进修与培训1984.03 — 1985.01： 华东师范大学物理系理论物理进修班学习1986.09 — 1988.07： 辽宁大学理论物理助教班，学习理论物理硕士研究生课程1993.09 — 1994.07： 北京师范大学物理系做国内访问学者工作经历1981.07： 山西大同大学物电学院（雁北师范专科学校、雁北师范学院）任教,教授2001.07： 雁北师范学院学位办主任2001.08： 被聘为南昌大学兼职硕士生导师2007.01： 山西大同大学研究生处处长2008.12： 被聘为中北大学兼职博士生导师二、主要学术成果1. Ren Zhao, Hui-Hua Zhao, Meng-Sen Ma, Li-Chun Zhang，On the critical phenomenaand thermodynamics of charged topological dilaton AdS black holes，Eur. Phys. J. C (2013) 73:26452.Lichun Zhang, Huaifan Li, Ren Zhao, Ronggen Cai, The Entropy of A Dielectric Black Hole, Modern Physics Letters A , 2013, 28 (07): 1350009 3. Ren Zhao, Mengsen Ma, Huaifan Li, Lichun Zhang, On Thermodynamics of Charged andRotating Asymptotically AdS Black Strings ，Advances in High Energy Physics ，Volume 2013 (2013), Article ID 371084, 7 pages4.Huihua Zhao, Guangliang Li, Lichun Zhang, Hawking and Unruh Effects of a 5-Dimensional Minimal Gauged Supergravity Black Hole by a Global Embedding Approach, En tropy 2013, 15, 1057-10685.Ren Zhao, Lichun Zhang, A new explanation for statistical entropy of charged black hole,SCIENCE CHINA Physics,Mechanics & Astronomy, 2013, 56(9): 1632-16356.Lichun Zhang, Huaifan Li，Huihua Zhao, Ren Zhao. Analytic study of properties ofholographic superconductors with Weyl corrections, International Journal of Theoretical Physics, Int J Theor Phys (2013) 52: 2455–24637.Lichun Zhang, Huaifan Li, Ren Zhao,Ronggen Cai. Entanglement entropy of acousticblack hole in Bose-Einstein Condensatem. Astrophysics and Space Science: Astrophys Space Sci (2013) 344:451–4548.Huaifan Li，Huihua Zhao, Lichun Zhang, Quantum statistical entropy of dielectric blackhole, International Journal of Theoretical Physics: 2013，52(2) : 362-3679.Jianhua Shi, Shuangqi Hu, Ren Zhao, Entanglement entropy of a black hole and isolatedhorizon, Astrophysics and Space Science: Astrophys Space Sci (2013) 343:555–558 10.Huihua Zhao, Guangliang Li, Lichun Zhang, Generalized uncertainty principle andentropy of three-dimensional rotating acoustic black hole, Physics Lett. A 2012, 376: 2348-235111.Ren Zhao, Lichun Zhang, Huihua Zhao, Quantum statistical entropy of Schwarzchild-deSitter spacetime Astrophysics and Space Science: 2012, 341: 675-67912.Ren Zhao，Lichun Zhang Hawking radiation from a dielectric black hole，AstrophysSpace Sci (2012) 338，295–30013.Cao Shuo, Zhu zonghong, Zhao Ren, Testing and selecting dark energy models with lensredshift data, PHYSICAL REVIEW D 84, 023005 (2011)14.Lichun Zhang, Huaifan Li and Ren Zhao Thermodynamics of the Reissner-Nordstrom-deSitter black hole, SCIENCE CHINA Physics, Mechanics & Astronomy 2011，54(8):1384-138715.Lichun Zhang, Huaifan Li and Ren Zhao Hawking and Unruh effects of the cosmologicalhorizon in a higher-dimensional Kerr-de Sitter spacetime by the global embedding approach，Europhyisics Letter. 2011(94) :4000316.张丽春，李怀繁，赵仁. 利用新的整体嵌入方法研究高维旋转黑洞的Hawking效应和Unruh效应, 物理学报 2011，60(8): 08040317.Lichun Zhang, Huaifan Li, Ren Zhao, Yueqin Wu, Thermodynamics of the five-dimensional Schwarzschild-de Sitter black hole, Astrophys Space Sci, 2011，335(2):523-52718.Lichun Zhang, Huaifan Li, Ren Zhao. Tunneling mechanism in higher-dimensionalrotating black hole with a cosmological constant in the approach of dimensional reduction，Astrophys Space Sci (2011) 333: 457-46219.Lichun Zhang, Huaifan Li, Ren Zhao. Hawking radiation from a rotating acoustic blackhole, Phys. Lett. B,2011, 698: 438-44220.Lichun Zhang，Hai Lin, Huaifan Li, Ren Zhao. Radiation spectrum of rotating Gödel blackhole and correction entropy，Chines Physics C，2011，35（4）：339-34321.张丽春，林海，李怀繁，赵仁，Kerr-Newman 时空中带电旋转粒子的Hawking辐射，中国科学G辑：物理、力学、天文学，2011，41（3）：221-22622.Ren Zhao, Li-Chun Zhang,Yue-Qin Wu, Huai-Fan Li，Temperature and Energy of 4-Dimensional Axisymmetric Black Holes from Entropic Force，Int J Theor Phys, 2011 50(4): 244-25023.Li Chun Zhang, Yue Qin Wu, Huai Fan Li, and Ren Zhao，Radiation Spectrum andCorrection to the Entropy of the Kerr-(anti)de Sitter Black Hole in all Dimensions，Chinese Journal of Physics, 2010, 48(4): 439-45024.张丽春，李怀繁，赵仁，Schwarzchild-de Sitter 黑洞的热力学性质，物理学报 2010，59(12):8994-899825.Zhang Lichun，Li Huaifan, Zhao Ren, Radiation spectrum and entropy correction of blackholes in Horava-Lifshitz gravity，Europhyisics Letter. 2010(89) :2000826.Zhao Ren, Li Huaifan, Zhang Lichun, Wu Yueqin, Hawking radiation and entropy in deSitter spacetime, Astrophys Space Sci (2010) 330: 361–36527.赵仁，张丽春，李怀繁 Kerr-Newman黑洞的辐射谱 物理学报 2010，29(5): 2982-298628.Zhang Lichun, Li Huaifan, Wu Yueqin, Zhao Ren Hawking Radiation Spectrum andEntropy Correction of Apparent Horizon in a FRW Universe Int J Theor Phys, 2010, 49(4): 1587-159429.张丽春，赵仁 Kerr-Newman-de Sitter 黑洞辐射谱和熵修正 物理学报 2010，59(4): 2217-222230.Zhao Ren, Li Huaifan, Zhang Lichun, Wu Yueqin Radiation spectrum of a high-dimensional rotating black hole SCIENCE CHINA Physics, Mechanics & Astronomy 2010，53(3):504-50731.Ren Zhao, Li-Chun Zhang, and Huai-Fan Li, Hawking radiation of a Reissner–Nordström–de Sitter black hole, General Relativity and Gravitation. 2010, 42(4): 975-98332.Zhao Ren, Zhang Lichun, Li Huaifan, hawking radiation of charged particles in reissner-nordstrom black hole, Commun. Theor. Phys. (Beijing, China), 2010,53 (3): 499–502 33.Zhang Lichun, Li Huaifan, Zhao Ren, radiation spectrum and correction entropy of (n+4)-dimensional kerr-(A)dS black hole, Int J Theor Phys, 2010, 49(4): 791-79734.Zhao Ren, Zhang Lichun, Wu Yueqin, Li Huaifan, Generalized uncertainty principle andtunneling radiation of the SAdS5 black hole, Chin. Phys. B, 2010, 19(1): 01040235.Zhao Ren, Zhang Lichun, Li Huaifan, Wu Yueqin. Hawking radiation of a high-dimensional rotating black hole, The European Physical Journal C. 2010, 65(1): 289-293 36.Li Huaifan, Zhang Shengli, Zhao Ren. General Radiation Spectrum of a Kerr-NewmanBlack Hole, Chinese Journal of Physics, 2009, 47(5): 618-62437.胡双启，张丽春，赵仁，Schwarzschild-de Sitter黑洞的Hawking辐射，物理学报. 2009, 58(10):6798-6802.38.Ren Zhao, Li-Chun Zhang, Yue-Qin Wu, and Huai-Fan Li, Generalized UncertaintyRelation and Hawking Radiation of the Black Hole , International Journal of Theoretical Physics. 2009,48(11): 3220-322739.Ren Zhao, Yue-Qin Wu, Li-Chun Zhang and Huai-Fan Li, Bekenstein-Hawkingcosmological entropy and correction term corresponding cosmological horizon of rotating and charged black string, Commun. Theor. Phys. 2009,52(6):264-26840.Huai-Fan Li, Sheng-Li Zhang, Yue-Qin Wu, Li-Chun Zhang and Ren Zhao, Hawkingradiation of Kerr–Newman–de Sitter black hole, The European Physical Journal C. 2009, 63(1): 133-13841.Li-Chun Zhang, Yue-Qin Wu, Huai-Fan Li, Ren Zhao, Hawking radiation and entropycorrection of a black hole, Europhyisics Letter. 2009 (86) :5900242.Ren Zhao, Yue-Qin Wu, Li-Chun Zhang, Hawking Radiation of Charged Particles from aRotating Black String, International Journal of Theoretical Physics. 2009, 48(5):1231-1238 43.Ren Zhao, Yue-Qin Wu, Li-Chun Zhang, Entropy of a rotating and charged black stringto all orders in the planck length, Chinese Physics B. 2009, 18(5):1749-178444.Ren Zhao, Yue-Qin Wu, Li-Chun Zhang and Huai-Fan Li, Hawking radiation of five-dimensional rotating black hole, The European Physical Journal C. 2009, 60(4): 685-69045.赵仁，张丽春，李怀繁. 广义测不准关系和三维BTZ黑洞熵. 物理学报. 2009, 58(4): 2193-2197.46.*L.-C. Zhang, H.-F. Li, R. Zhao, Canonical Entropy of Higher-Dimensional Reissner-Nordstroem Black Hole. Bulgarian Journal of Physics. 2007, 34(2) (34): 092-10247.赵仁，张丽春，李怀繁. 黑洞的Hawking辐射. 物理学报. 2008, 57(12), 7463-7466.48.Zhao Ren, Zhang Lichun, Wu Yueqin , Li Huaifan. Entropy of Four-DimensionalSpherically Symmetric Black Holes with Planck mun. Theor. Phys.2008,50(6):1327-133049.Zhao Ren, Zhang Lichun, Li Huaifan, Wu Yueqin. Entropy of Kerr-Newman Black Hole toAll Orders in the Planck Length. International Journal of Theoretical Physics. 2008, 47(12): 3083-309050.Li-Chun Zhang, Huai-Fan Li, Ren Zhao and Yue-Qin Wu,Canonical entropy of black holein the generalized uncertainty principle. International Journal of Theoretical Physics.2008, 47 (7): 2021-2028（SCI: 310IF）51.Zhang Lichun, , Wu Yueqin, Li Huaifan, Zhao puting the Entropy of Kerr-Newman Black Hole Without Brick Walls Method, International Journal of Modern Physics A, 2008,23(20): 3155-316352.Zhang Shaoming, Hu Shuangqi, Zhao Ren, Entropy of toroidal black hole to all orders inthe Planck length, IL NUOVO CIMENTO, 2008,123(2): 247-255（SCI:363OF）53.张丽春，武月琴，赵仁，带电黑洞Bekenstein-Hawking熵的修正值,中国科学G辑：物理、力学、天文学，2008，38（9）：1113－111954.Zhang Lichun, Wu Yueqin, Zhao Ren, Correction value to charged bekenstein-Hwakingblack hole entropy, Sciencein China Series G: Physics, mechanics & Astronomg, 2008, 51(9): 1214-1220（SCI:335UO）55.Zhao Ren, Wu Yueqin, Zhang Lichun, Canonical entropy and phase transition of rotatingblack hole, Chinese Physics Letters, 2008,25(7):2385-2388(SCI:321SE)56.Zhang Lichun, Wu Yueqin, Li Huaifan, Zhao Ren.Generalized Uncertainty Principle andThermodynamic Quantities of SAdS5 Black Hole, Commun. Theor. Phys., 2008, 50(1): 97-100(SCI: 333AQ,IF:0.726)57.Li Huaifan, Zhang Shengli, Wu Yueqin, Zhao Ren, Entanlement Entropy of The Six-Dimensional Horwitz Strominger Black Hole, International Journal of Modern Physics A, 2008,23(13): 1963-1972(SCI: 321JE)58.张丽春, 胡双启, 李怀繁, 赵仁. 轴对称黑洞的量子统计熵. 物理学报, 2008, 57(6): 3328-333259.Zhao Ren, Wu Yueqin, Zhang Lichun. Generalized uncertainty principle andthermodynamic quantities of the Achucarro-Ortiz black hole. Modern Physics Letters A, 2008,23(11): 839-84660.Zhao Ren, Zhang ShengLi. Quantum statistical entropy corresponding to cosmic horizonin five-dimensional spacetime. Sciencein China Series G: Physics, mechanics & Astronomg, 2008, 51(2): 140-14661.Liu Xinmei, Zhang Lichun, Wu Yueqin, Zhao Ren.Entropy of Garfinkle-Horowitz-Strominger dilaton black holes with the planck length. IL Nuovo Cimento, 2008, 122B(8): 909-91762.Zhang Ya, Hu Shuangqi, Zhao Ren, Li Huaifan. Generalized uncertainty principle andcorrection value to the kerr black hole Entropy. International Journal of Theoretical Physics, 2008, 47(1): 520-525(SCI: 269WO)63.Zhao Ren, Zhao Haixia, Hu Shuagnqi. General Logarithmic Corrections to Bekenstein-Hawking Entropy. Modern Physics Letters A, 2007, 22(23): 1737-1743, gr-qc/0609080(SCI: 243EV)64.赵 仁, 张丽春, 张胜利. 正则黑洞熵与相变. 物理学报, 2007, 56(12): 7355-7358(SCI: 246PI,EI: 080311033748)65.Zhao Ren, Zhang Lihun, Wu Yueqin. Calculating Entropy of Plane Symmetry Black Holevia Generalized Uncertainty Relation. International Journal of Theoretical Physics, 2007, 46: 3128-3134(SCI: 235LS)66.赵 仁, 张胜利. 五维时空中宇宙视界对应的量子统计熵. 中国科学 G辑 物理 力学 天文学,2007, 37, (4): 434-43967.Zhao Ren, zhang Lichun, Zhang Shengli. Canonical Entropy of Reissner-Nordstrom BlackHole. International Journal of Theoretical Physics, 2007, 46(8): 2158-2167(SCI: 215KR)68.赵 仁, 张丽春, 张胜利. 正则黑洞熵. 物理学报, 2007, 56(7):3719-3722(SCI:191ME)69.Zhao Haixia, Li Huaifan, Hu Shuangqi, Zhao Ren. Generalized uncertainty principle andblack hole Entropy of higher-dimensional de sitter spacetime. Commun. Theor. Phys., 2007, 48(3): 465-468(SCI: 212MJ)70.Zhao Ren, Li Huaifan, Hu Shuangqi. Hawking Radiation as Tunneling for RotatingCharged Black Strings. Chinese Journal of Physics, 2007, 45(1): 32-40(SCI: 138BL)71.Zhao Ren, Zhang Shengli. Generalized uncertainty principle and black hole entropy.Physics Letters B, 2006, 641: 208-211(SCI: 093WS,IF:5.043)72.Zhao Ren Zhang Shengli. Canonical entropy of three-dimensional BTZ black hole.Physics Letters B, 2006,641: 318-322; gr-qc/0608122(SCI: 092ZS,IF:5.043)73.Hu Shuangqi, Zhang Lichun, Zhao Ren. Black Cylinder Entropy Without Brick Walls. ILNuovo Cimento, 2006, 121B (03): 221-227 (SCI: 074ZQ, IF: 0.324)74.Zhao Ren, Zhang Lichun, Hu Shuangqi. (Anti)-de Sitter Black Hole Entropy and theGeneralized Uncertainty Principle. Commun. Theor. Phys., 2006, 45(4): 635-638(IF:0.726) 75.Zhao Ren, Wu Yueqin, Zhang Shengli. Quantum Statistical Entropy of the Five-Dimensional black hole. Commun. Theor. Phys., 2006, 45(5): 849-852(SCI:047IK, IF:0.726) 76.Zhao Ren, Li Huaifan, Zhang Shengli. Hawking Radiation as Tunneling for Kerr-Newman-de Sitter black hole. Romanian Journal of Physics, 2006,51(7-8): 709-71777.赵仁, 张丽春, 胡双启. 探讨黑洞Hawking辐射的新方法--量子统计法. 物理学报, 2006, 55(8):3898-3901(SCI: 073MF, IF:1.051)78.赵仁, 张丽春, 胡双启. 黑洞的统计熵. 物理学报, 2006, 55(8): 3902-3905(SCI: 073MF,IF:1.051)79.Zhao Ren, Hu Shuang-Qi. Quantum Statistical Entropy of the 5-Dimensional Stringyblack hole. Chinese Journal of Physics, 2006, 44(3): 172-179(SCI: 053ZI)80.Zhao Ren, Hu Shuang-Qi. Quantum statistic entropy of three-dimensional BTZ blackhole. International Journal of Theoretical Physics. 2006, 45(6): 1163-1170(SCI: 060WP) 81.Zhao Ren, Zhang Sheng-Li. Cardy-Verlinde Formula and Thermodynamics of Black Holein Higher Dimensional Space-Time. International Journal of Theoretical Physics, 2006,45(6): 1116-1123(SCI: 060WP, IF: 0.389)82.Zhang Lichun, Wu Yueqin, Li Huaifan. Canonical entropy of higher-dimension black hole.IL Nuovo Cimento, 2006, 121B(7): 743-75083.Zhao Ren, Zhang Shengli. Cardy-Verlinde formula and logarithmic correction of D-dimensional global monopole black hole. Chinese Journal of Physics, 2005, 43(6): 1044-1050(SCI:995QS, IF:0.440)84.Zhao Ren, Zhang Shengli. Entropy Correction for Kerr Black Hole. Commun. Theor.Phys., 2005, 44(6): 1037-1040(SCI:001LC, IF:0.872)85.Hu Shuangqi, Zhao Ren. Uncertainty relation and black hole entropy of Kerr spacetime.Chinese Physics, 2005, 14(07): 1477-1481(SCI: 943CJ)86.Zhao Ren, Zhang Zizhen, Zhang Shengli. Uncertainty relation and black hole entropy ofNUT-Kerr-Newman spacetime. IL Nuovo Cimento, 2005, 120B (1): 61-67(SCI: 963CM) 87.Zhao Ren, Wu Yueqin, Zhang Lichun. The Nernst theorem and the statistical entropy ofThe NUT-Kerr-Newman black hole. Bulgarian Journal of Physics, 2005,32: 1-988.Zhang Zizhen, Zhang Lichun. Calculating the entropy of Garfinkle- Horowitz- Stromingerdilaton without brick-wall method. IL Nuovo Cimento, 2004, 119B(10): 1001-1006(SCI: 928TH)89.Zhao Ren, Zhang Shengli. Statistical entropy of the A torus-like black hole. IL NuovoCimento, 2004, 119B(6): 557-563(SCI: 901EJ)90.Hu Shuangqi, Zhao Ren. Uncertainty Relation and Black Hole Entropy of ToroidalSpacetime. International Journal of Geometric Methods in Modern Physics, 2004, 1(6):731-737(SCI: 888RZ)91.Ding Tianran, Zhao Ren. Quantum Statistical Entropy of Kerr-de Sitter Black Hole.International Journal of Geometric Methods in Modern Physics, 2004, 1(1):159-166(SCI: 885MF)92.Zhao Ren, Wu Yueqin, Zhang Shengli. Quantum Statistical Entropy of d-dimensionalHorowitz -Strominger Black Hole. Gen. Rel. Grav., 2004,36(11): 2539-2547(SCI:875EV) 93.Zhao Ren, Zhang Li-Chun. Statistical entropy of a rotating higher-dimensional blackholes. IL Nuovo Cimento, 2004, 119B(1): 33-40(SCI: 859OB)94.张丽春, 赵仁. 具有双旋转参数5-维黑洞的Cardy-Verlinde公式. 物理学报, 2004, 53(12):4435-4438(SCI: 775NT)95.赵仁, 张丽春. 黑洞的量子统计熵. 数学物理学报, 2004, 24A(5): 513-52096.Zhao Ren, Zhang Sheng-Li. Dilatonic black hole entropy without brick walls. Gen. Rel.Grav., 2004, 36 (9): 2123-2130(SCI:847NN)97.Zhang Li-Chun, Zhao Ren, Lin Hai. Horowitz-Strominger Black Hole Entropy WithoutBrick Wall. Chinese Physics Letters, 2004,21(6)1009-1012(SCI: 831MM)98.Zhao Ren, Hu Shuang-Qi. Reissner-Nordstrom black hole without brick walls. IL NuovoCimento, 2004, 119B(2): 149-155(SCI: 859OC)99.Zhang Li-Chun, Wu Yue-Qin, Zhao Ren. Quantum Statistical Entropy for Kerr-de SitterBlack Hole. Chinese Physics, 2004, 13(06): 974-978100.Ding Tianran, Wu Yueqin, Zhang Lichun. Bosonic and fermionic entropy of black holes with different temperatures on horizon surface. Chinese Physics, 2004, 13(02):268-272(SCI: 770UK)101.Zhao Ren, Wu Yue-Qin, Zhang Li-Chun. Quantum Statistical Entropy of Sen Black Hole.Turkish Journal of Physics, 2004, 28(2): 81-87(EI: 04238192675)102.张丽春, 赵 仁. Sen黑洞熵与能斯特定理. 物理学报, 2004, 53(2): 362-366(SCI: 775NT) 103.Zhao Ren, Guo Yong, Ding Bing Jun. The entropy of a Kim black hole and the Nernst theorem. IL Nuovo Cimento, 2003,118B(7) 685-691(SCI: 937PT)104.Zhao Ren, Wu Yue-Qin, Zhang Li-Chun. Spherically symmetric black-hole without brick walls. Classical and Quantum Gravity, 2003, 20(22): 4885-4890(SCI: 752AC)105.Zhao Ren, Wu Yue-Qin, Zhang Li-Chun. Nernst Theorem and the Statistical of 5-Dimensional Rotating black Hole. Communications in Theoretical Physics, 2003, 40(6): 745-748(SCI: 759LL)106.Zhao Ren, Wu Yue-Qin, and Zhang Li-Chun. Kaluza-Kelin black-hole entropy by quantum statistics. International Journal of Theoretical Physics, 2003, 42(4): 809-816(SCI: 695MH) 107.Zhao Ren, Guo Yong, Ding Bing Jun. Statistical Entropy of Higher-Dimensional Black Hole. Journal of the Korean Physical Society, 2003, 43(6): 987-990(SCI: 754JT)108.Zhao Ren, Wu Yue-Qin, Zhang Li-Chun. Bosonic and Fermionic Entropy for Dilaton Black Hole. Bulgarian Journal of Physics. 23(2003)(in press)(1)(2)U U109.Zhao Ren, Wu Yue-Qin, Zhang Li-Chun. Entropy of N-dimensional spherically symmetric charged black hole. Communications in Theoretical Physics, 2003, 39(4): 425-428(SCI: 671AF)110.韩伏龙, 张丽春, 赵 仁. A torus-like 黑洞与熵能斯特定理. 数学物理学报, 2003, 23A(6): 655-659111.张丽春, 韩伏龙, 赵 仁. Reissner-Nordstrom 黑洞几何中Dirac场的统计熵与能斯特定理.数学物理学报, 2003, 23A(1): 77-83112.赵 仁, 张丽春. 黑洞热力学关系式. 雁北师范学院学报, 2002, 18(5): 1-6113.赵 仁, 张丽春. 平面对称黑洞的统计熵. 物理学报, 2002, 51(1): 21-24(SCI: 512CZ)114.Zhao Ren, Zhang Lichun. Statistical entropy of Kerr black hole. International Journal of Modern Physics Letters D, 2002, 11(9): 1381-1387(SCI: 641FD)115.Zhao Ren, Zhang Junfang, Zhang Lichun. Quantum statistical entropy of black hole. Gen.Rel. Grav., 2002,34(12): 2063-2073(SCI: 616NN)116.Zhao Ren, Zhang Lichun, Yang Chunhua. Statistical entropy of a rotating cylindrical black hole. Chinese Journal of Physics, 2002, 40(5): 505-511(SCI: 604YC)117.Zhao Ren, Wu Yueqin, Zhang Lichun. Bosonic and frmionic entropy of tree-dimensional black hole. IL Nuovo Cimento, 2002, 117B(3): 367-372(SCI: 592UZ)118.Zhao Ren, Zhang Lichun. Entropy of Riessner-Nordstrom-anti-de Sitter black hole.Czechoslovak Journal of Physics, 2002, 52(6): 775-780(SCI: 574QR)119.Zhao Ren, Zhang Junfang, Zhang Lichun. Entropy of dilatonic black hole. International Journal of Theoretical Physics, 2002,41(7): 1369-1375(SCI: 582JN)120.Zhao Ren, Zhang Lichun. Statistical entropy of Vaidy-de Sitter black hole. IL Nuovo Cimento, 2002, 117B(1): 69-73(SCI: 564KC)121.Zhao Ren, Zhang Lichun. Entropy black hole. IL Nuovo Cimento, 2002, 117B(1): 129-136(SCI: 564KC)122.赵 仁, 张丽春. Kerr-Newman黑洞的统计熵. 物理学报, 2002, 51(6): 1167-1170(SCI: 559XE) 123.Zhao Ren, Zhang Junfang, Zhang Lichun. Statistical entropy of black cylinder. Gen. Rel.Grav., 2002, 34(5): 571-576(SCI: 564TJ)124.张丽春, 武月琴, 赵 仁. 轴对称Einstein-Maxwel-Dilaton-Axion黑洞熵与能斯特定理. 数学物理学报, 2002, 22A(1): 115-120125.Zhao Ren, Zhang Junfang, Zhang Lichun. Entropy of Reissner--Nordstrom--de Sitter black hole in non-thermal-equilibrium. Communications in Theoretical Physics, 2002, 37(1)45-48 (SCI: 515WT)126.Zhao Ren, Zhang Junfang, Zhang Lichun. Statistical Entropy of Horowitz-Strominger Black Hole. Communications in Theoretical Physics, 2002,37(5): 564-566(SCI: 558RF) 127.Zhang Junfang, Zhang Lichun, Zhao Ren. Statistical entropy of a charged black hole. IL Nuovo Cimento, 2001, 116B(8): 959-963(SCI: 500UE)128.Zhao Ren, Zhang Junfang, Zhang Lichun. The Nernst theorem and statistical entropy in 1+1 dimensional charged black hole. IL Nuovo Cimento, 2001, 116B (6): 707-711(SCI: 486TC)129.Zhao Ren, Zhang Junfang, Zhang Lichun. Statistical entropy of axial symmetry Einstein-Maxwel- Dilaton-Axion black hole. Bulgarian Journal of Physics, 2001, 28(5/6): 200-208 130.Zhao Ren, Zhang Junfang, Zhang Lichun. Statistical entropy of a cylindrical black hole.Il Nuovo Cimento, 2001, 116B(10): 1181-1186(SCI: 524VL)131.Zhang Lichun, Zhao Ren, Wu Yueqin. The entropy of the Dirac field on the background of the Reissner--Nordstrom black hole. IL Nuovo Cimento, 2001, 116B(5): 555-562(SCI: 477KA)132.Zhang Lichun, Zhao Ren and Wu Yueqin. Statistical entropy in Kaluza--Klein Geometry.IL Nuovo Cimento, 2001, 116B(3): 335-339(SCI: 476BX)133.Zhao Ren, Zhang Lichun. The Static Spherically Symmetric metric of a Schwarzschild black hole Surrounded by the Radiation Field. IL Nuovo Cimento, 2001,116B(5): 509-514(SCI: 477KA)134.Zhao Ren, Zhang Lichun, and Wu Yueqin. Nernst theorem and entropy of the axisymmetric Einstein-Maxwell-Dilaton-Axion black hole. International Journal of Theoretical Physics, 2001, 40(9): 1657-1664(SCI: 479XH)135.Zhao Ren, Zhang Junfang, Zhang Lichun. Entropy of Schwarzschild-De Sitter Black Hole in Non-Thermal-Equilibrium. Modern Physics Letters A , 2001, 16 (11): 719-723(SCI: 434TN)136.Zhao Ren, Zhang Junfang, Zhang Lichun. Statistical entropy in Reissner-Nordstrom black hole. Nuclear Physics B, 2001,609: 247-252(SCI: 464EH)137.Wu Yueqin, Zhang Lichun, Zhao Ren. Black Hole and Cosmic Entropy for Schwarschild-de Sitter space-time. International Journal of Theoretical Physics, 2001, 40(5): 1001-1008(SCI: 438AW)138.赵 仁, 张丽春. Kim 黑洞熵与能斯特定理. 物理学报, 2001, 50(4): 593-596(SCI: 419KJ, EI: 04057987069)139.赵 仁, 张丽春. Reissner--Nordstrom几何中标量场的统计熵与能斯特定理. 物理学报, 2001, 50(6): 1015-1018(SCI: 438TC)140.Zhao Ren, Zhang Lichun. The Nernst theorem and the entropy of a cylindrical black hole.Modern Physics Letters A , 2000, 15(35): 2165-2170(SCI: 394DV)141.赵 仁, 张丽春. De Sitter宇宙的稳定性. 数学物理学报, 2000, 20增: 583-588142.Zhao Ren, Zhang Lichun, Wu Yueqin. The Nernst theorem and the entropy of the Reissner-Nordstrom black hole. Gen. Rel. Grav., 2000, 32(8): 1639 -1646(SCI: 348CP) 143.赵仁, 张丽春. 充满物质的Friedmann-Robertson-Walker宇宙的稳定性. 物理学报, 2000, 49(8): 1644-1647(SCI: 343CW)144.张丽春, 赵仁. 球对称带电动态时空中Dirac粒子的Hawking效应. 数学物理学报, 1999,19(5): 573-578145.Zhang Lichun, Wu Yueqin, Zhao Ren. Hawking Effect of the Dirac Particles of Evaporating146.张丽春、张全龙、赵仁. 结合物理教学在学生中开展科学教育. 雁北师范学院学报 6(1999) 18-20三、主持或参与的教研、科研项目纵向课题：1.李怀繁、赵 仁、郭雄英、赵惠华、刘芳：山西省青年科技研究基金“规范/引力对偶在强耦合凝聚态系统中的应用，（2012021003-4）”2012年1月－2014年12月2.李怀繁、赵 仁、史建华、郭雄英、刘先锋：AdS/CFT 对应在凝聚态物理中的应用（11205097），国家自然科学青年基金。

利用冯诺依曼熵获得最大纠缠态的形式朱孟正;赵春然;李洪俊;张东杰【摘要】纠缠在量子信息处理中有许多重要的应用,正如Bell态对量子通信的实施是必不可少的.考虑如何得到Bell态,本文提出了一种用冯· 诺依曼熵求解二体或三体系统中最大纠缠态表示形式的方法.计算二体或三体系统的量子态的冯· 诺依曼熵,并将约化密度算符与用Bloch矢量表示的密度算符进行比较.根据密度算符具有正的、厄密性的特点,得到了最大纠缠态解析式,如Bell态和GHZ态.【期刊名称】《吉林师范大学学报（自然科学版）》【年(卷),期】2018(039)002【总页数】5页(P78-82)【关键词】冯·诺依曼熵;纠缠态;密度算符【作者】朱孟正;赵春然;李洪俊;张东杰【作者单位】淮北师范大学物理与电子信息学院,安徽淮北235000;淮北师范大学信息学院,安徽淮北235000;淮北师范大学物理与电子信息学院,安徽淮北235000;淮北师范大学物理与电子信息学院,安徽淮北235000;淮北师范大学物理与电子信息学院,安徽淮北235000【正文语种】中文【中图分类】O413.10 IntroductionThe key feature of quantum mechanics that lies behind quantum information theory is quantum entanglement.Quantum entanglement refers to correlations between the results of measurements made on distinct subsystems of a composite system that can not be explained in terms of standard statistical correlations between classical properties inherent in each subsystem.For the bipartite quantum systems，a correlation between two subsystems is simply the statement that if a measurement of one subsystem yields the result A then a measurement on the second subsystem will yield the result B with some probability.Perfect correlation occurs when the second result is certain，given the outcome of the first[1-2].It has become clear that entanglement is a new quantum resource for tasks that cannot be performed by means of classical resources.It can be manipulated，broadcast，controlled and distributed.Remarkably，entanglement is a resource which，though it does not carry information itself，can help in such tasks as the reduction of classical communication complexity，entanglement-assisted orientation in space，quantum estimation of a damping constant，frequency standards improvement，and clock synchronization.Entanglement plays a fundamental role in quantum communication between parties separated by macroscopic distances[3-5].For these tasks，the maximally entangled state is an indispensable quantum resource.The Bell states are the “canonical” maximally entangled states in the bipartite systems[6].Have we ever considered how the Bell states are given? This article presents a method for solving the representation of the maximally entangled states intwo-particle systems using von Neumann entropy.Then we generalize this approach to the three-body entanglement problem[7].1 Von Neumann entropy and the maximally entangled stateFor any pure state of two parties，for instance，a pure state of two qubits can be written as|ψ〉AB=c0|00〉+c1|01〉+c2|10〉+c3|11〉.(1)A unique measure of bipartite entanglement for pure states is given by the partial von Neumann entropy.The von Neumann entropy of a state is defined asS(ρ)=-Tr(ρlogρ)，(2)where the symbol ρ is the density operator for the system and Tr(…) denotes the trace operation.We can obtain the density operator associated with the quantum state in Eq.(1)，(3)The entanglement of the partly entangled pure state in Eq.(3) can be naturally parametrized by its entropy of entanglement[8]，defined as the von Neumann entropy of either ρA or ρB，S(ρAB)=S(ρA)=S(ρB).(4)We choose the standard basis to calculate the partial trace.For the densityoperator in Eq.(3)，we can obtain(5)where TrB refers to the partial trace over mode B.Analogously，(6)We diagonalise ρA or ρB.When the reduced density operator ρ is written in this diagonal form，our von Neumann entropy in Eq.(2) becomes(7)where the symbols ρn are the associated(non-negative) eigenvalues of the reduced density operator ρ diagonalised，which sum to unity，that is to the diagonalization，the reduced density operator ρA and ρB can be written as(8)where an d ζ≡4|c1c2-c0c3|2.Obviously，0≤ζ≤1.By making use of the diagonal representation of the reduced density operator in Eq.(8)，we write von Neumann entropy in the form：S(ρAB)=S(ρA)=S(ρB)=-ρ+logρ+-ρ-logρ-.(9)Any two-by-two matrix can be written as a weighted sum of the four Pauli operators.This means，in turn，that any operator associated with our qubit can also be expressed in terms of these operators.In particular，we can write the density operator in the form：(10)where I is the identity operator，r=(u，ν，w) is a Bloch vector，and σ=(σx，σy，σz) is the vector operator[9].Here Eq.(10)，the factor 1/2 ensures that Tr(ρ)=1.The density operator ρ is a positive Hermitian operator.The Hermiticity of ρ ensures that u，ν，and w are real.For the two-state system，the density operator of Eq.(10) can be written in the diagonal form：ρ=ρ+|ρ+〉〈ρ+|+ρ-|ρ-〉〈ρ-| .(11)where the states |ρ+〉and |ρ-〉are the eigenvectors of ρ correspondingto the eigenvalues Neumann entropy can be written as the equation(9)，but ρ± are described by the variable r.We have delineated Figure 1 about the von Neumann entropy as a function of the variable r.The positivity of the density operator ρ requires that u2+ν2+w2≤1.It is worth noting that the eigenvectors of ρ，namely |ρ+〉and |ρ-〉，are also the eigenvec tors of the operator r·σ corresponding to the eigenvalues ±r.If the vector’s tip of r lies on the surface of the Bloch sphere(r=1)，the diagonal density operator in Eq.(11) reduces the pure state |ρ+〉〈ρ+|.Ifr<1，the Bloch vector describes a point inside the Bloch sphere and corresponds to a mixed state.The farther the point is from the surface，the higher the degree of mixing of the mixed state is.This is to say，the resultis a more mixed state with a greater entropy.When the entropy of the subsystem reduced states are maximal，such states are called maximally entangled.The maximally entangled state of two subsystems associatedwith Eq.(1) requires r=0 from Fig.1.Fig.1 The von Neumann entropy versus the variable rAccording to the condition r=0，we can obtain the real parameteru=ν=w=0 due to the Hermiticity of ρ.Compared Eq.(5) and Eq.(6)with Eq.(10)，we can also write the following relationship：|c0|2+|c1|2-|c2|2-|c3|2=0，|c0|2-|c1|2+|c2|2-|c3|2=0，|c0|2+|c1|2+|c2|2+|c3|2=1，|c1c2-c0c3|=1/2(12)in the condition of the maximally entangled state.We choose the real coefficients c0，c1，c2，and c3 for simplicity.The individual equation in Eqs.(12) is not linearly independent of the other，for example，the last equation.By solving Eqs.(12)，we can obtain the coefficients of Eq.(1) for the maximally entangled state as follows.If and c1=c2=0；if andc0=c3=0.This result exactly corresponds to the Bell states for the maximally entangled subsystems.The four Bell states are conventionally written in the form(13)They are known as the four maximally entangled two-qubit Bell states.The von Neumann entropy of this density operator of the Bell states is positive and maximal.For the quantum state of two qubits，the Bell states of have a special prominence.The reasons for this include their simplicity and the fact that they have been realized in a number of diverse experiments.Just as Bell states are essential for the implementation of quantumcommunication with perfect fidelity，the importance of such a state in the distribution of bipartite entanglement is obvious.Certainly，multipartite maximally entangled states also play many crucial roles in quantum computation and quantum communication[10].Then we this approach is also generalized to solve the maximally entangled states of the three-body entanglement.For any pure state of tripartite，for instance，a pure state of three qubits can be written as|ψ〉ABC=c0|000〉+c1|001〉+c2|010〉+c3|011〉+c4|100〉+c5|101〉+c6|110〉+c7|111〉.(14)We can obtain the density operator associated with the quantum tripartite state in Eq.(14)，ρABC=|ψ〉ABC〈ψ|.(15)For the tripartite density operator，we choose the standard basis to calculate the partial trace in order to obtain(16)whereρA11≡|c0|2+|c1|2+|c2|2+|c3|2，ρB11≡|c0|2+|c1|2+|c4|2+|c5|2，ρC11≡|c0|2+|c2|2+|c4|2+|c6|2，Compared Eqs.(16) with Eq.(10) in the condition of r=0，we can obtain the coefficients of Eq.(14) in order to write the maximally entangled state of tripartite system as follows(17)Analogously，for simplicity we have chosen the real coefficients ci(i=0，1，2，…，7).They are known as the eight maximally entangled Greenberger-Horne-Zeilinger(GHZ)states[11].The GHZ state is a certain type of entangled state that involves at least three subsystems.The GHZ states are used in several protocols in quantum communication and cryptography，for example，in secret sharing.Thus the GHZ-state and the W-state represent two very different kinds of tripartite entanglement.In a certain sense，the W-state is “less entangled” than the GHZ-state.Therefore，the W-state does not belong to our solution.2 ConclusionThe degree which state in a quantum system consisting of two “particles” is entangled is measured by the von Neumann entropy of either of the two reduced density operators of the state.When the entropy of the subsystem reduced states are maximal，such states are called maximally entangled.We calculate the von Neumann entropy of the pipartite or tripartite systems and compare the reduced density operator with the density operator in the form of the Bloch vertor.According to the character that the density operator ρ is a positive Hermitian operator，we obtain the maximally entangled states such as the Bell states and the GHZ states. References【相关文献】[1]GERRY C C，KNIGHT P L.Introductory quantum optics[M].Cambridge：Cambridge University Press，2005.[2]PAN J W，CHEN Z B，LU C Y，et al.Multiphoton entanglement andinterferometry[J].Rev Mod Phys，2012，84(2)：777-838.[3]HORODECKI R，HORODECKI P L，HORODECKI M L，et al.Quantumentanglement[J].Rev Mod Phys，2009，81(2)：865-942.[4]SCHMID C，KIESEL N，WEBER U K，et al.Quantum teleportation and entanglement swapping with linear optics logic gates[J].New J Phys，2009，11：33008-1-33008-10. [5]ZHANG X L，WANG M L，YANG L L.Hawk-dovegame model of quantum under asymmetric information[J].Journal of Jilin Normal University(Natural Science Edition)，2011，32(4)：8-12.[6]EISERT J，CRAMER M，PLENIO M B.Colloquium：Area laws for the entanglement entropy[J].Rev Mod Phys，2010，82(1)：277-306.[7]AMICO L，FAZIO R，OSTERLOH A，et al.Entanglement in many-body systems[J].Rev Mod Phys，2008，80(2)：517-576.[8]BENNETT C H，BERNSTEIN H J，POPESCU S，et al.Concentrating partial entanglement by local operations[J].Phys Rev A，1996，53：2046-2052.[9]BARNETT S M.Quantum information[M].New York：Oxford University Press，2009.[10]DÜR W.Multipartit e entanglement that is robust against disposal of particles[J].Phys Rev A，2001，63(2)：020303-1-020303-4.[11]GREENBERGER D M，HORNE M A，SHIMONY A，et al.Bell’s theorem without inequalities[J].Am J Phys，1990，58(12)：1131-1143.。

第41卷第6期2023年12月沈阳师范大学学报(自然科学版)J o u r n a l o f S h e n y a n g N o r m a lU n i v e r s i t y(N a t u r a l S c i e n c eE d i t i o n)V o l.41N o.6D e c.2023文章编号:16735862(2023)06056804磁荷对H a y w a r d-A n t i-d eS i t t e r黑洞的全息互信息的影响李慧玲,张宁,张宝琪,李瑶(沈阳师范大学物理科学与技术学院,沈阳110034)摘要:H a y w a r d黑洞是爱因斯坦引力非线性耦合一个携带磁荷的电磁场的解析解,是非线性磁单极子引力场的简并结构㊂一般情况下,黑洞的内部会存在奇点,而 非奇异 黑洞是一种内部没有奇点的黑洞㊂H a y w a r d黑洞属于非奇异黑洞,此规则黑洞的对称性由磁势决定,带磁荷和不带磁荷的黑洞具有不同的微观结构㊂利用纠缠熵讨论磁荷对非奇异H a y w a r d-A n t i-d eS i t t e r黑洞中全息互信息的影响㊂结果表明,随着条带宽度(子区域)的增加,2个渐进子系统纠缠增大,且全息互信息随磁荷的增加而降低㊂除此之外,存在临界磁荷使得全息互信息为零,此时对偶的子区域之间不存在纠缠,磁荷取不同值时,全息互信息消失的条带宽度临界值是不同的㊂关键词:全息互信息;纠缠熵;磁荷;A d S黑洞中图分类号:P145.8文献标志码:Ad o i:10.3969/j.i s s n.16735862.2023.06.014E f f e c to fm a g n e t i cc h a r g e so nh o l o g r a p h i cm u t u a l i n f o r m a t i o no fH a y w a r d-A n t i-d e S i t t e r b l a c kh o l e sL IH u i l i n g,Z HA N GN i n g,Z HA N GB a o q i,L IY a o(C o l l e g e o f P h y s i c a l S c i e n c e a n dT e c h n o l o g y,S h e n y a n g N o r m a lU n i v e r s i t y,S h e n y a n g110034,C h i n a)A b s t r a c t:H a y w a r d b l a c k h o l ei sa n a n a l y t i c a ls o l u t i o n o f E i n s t e i n s g r a v i t a t i o n a ln o n l i n e a rc o u p l i n g o f a n e l e c t r o m a g n e t i c f i e ld c a r r y i n g m a g ne t i c c h a r g e s.I n g e n e r a l,t h e r e w i l l b es i n g u l a r i t i e s i n s i d eb l a c kh o l e s,a n d"n o n-s i n g u l a r"b l a c kh o l e sa r eb l a c kh o l e s w i t h o u t i n t e r n a l s i n g u l a r i t i e s,a n d H a y w a r d b l a c k h o l e sa r en o n-s i n g u l a r.H a y w a r d b l a c k h o l ei sad e g e n e r a t e s t r u c t u r eo f t h e n o n l i n e a rm a g n e t i cm o n o p o l e g r a v i t a t i o n a l f i e l d.T h e s y mm e t r y o f t h e r e g u l a r b l a c kh o l e i s d e t e r m i n e db y t h em a g n e t i c p o t e n t i a l,a n d t h em a g n e t i c c h a r g e a n d t h e n o n-m a g n e t i c c h a r g eh a v e d i f f e r e n tm i c r o s t r u c t u r e s.W e d i s c u s s t h e i n f l u e n c e o fm a g n e t i c c h a r g e o nh o l o g r a p h i cm u t u a li n f o r m a t i o n i nn o n s i n g u l a rH a y w a r d-A n t i-d eS i t t e r b l a c kh o l eb y u s i n g e n t a n g l e m e n t e n t r o p y.T h er e s u l t s s h o wt h a t t h e e n t a n g l e m e n t o f t h e t w o a s y m p t o t i c s u b s y s t e m s i n c r e a s e sw i t h t h e i n c r e a s e o f t h e s t r i p w i d t h(s u b r e g i o n),a n d t h e h o l o g r a p h i cm u t u a l i n f o r m a t i o nd e c r e a s e sw i t h t h e i n c r e a s e o f m a g n e t i c c h a r g e,I n a d d i t i o n,t h e r e i s a c r i t i c a lm a g n e t i c c h a r g e t h a tm a k e s t h e h o l o g r a p h i cm u t u a li n f o r m a t i o n z e r o,a n d t h e r e i s n o e n t a n g l e m e n t b e t w e e n t h e s u b r e g i o n s o f t h e d u a l i t y,a n dw h e n t h em a g n e t i c c h a r g et a k e sd i f f e r e n tv a l u e s,t h ec r i t i c a lv a l u eo ft h es t r i p e w i d t ho ft h eh o l o g r a p h i c m u t u a l i n f o r m a t i o nd i s a p p e a r i n g i s d i f f e r e n t.K e y w o r d s:h o l o g r a p h i cm u t u a l i n f o r m a t i o n;e n t a n g l e d e n t r o p y;m a g n e t i c c h a r g e;A n t i-d e S i t t e r(A d s)b l a c kh o l e收稿日期:20230713基金项目:辽宁省教育厅科学研究经费项目(L J KM20221474)㊂作者简介:李慧玲(1977 ),女,辽宁沈阳人,沈阳师范大学教授,博士㊂黑洞是广义相对论中最具有深远意义的预言之一,多年来,人们一直在研究宇宙中这个神秘天体㊂对于非奇异H a y w a r d -A d S 黑洞,带磁荷和不带磁荷的黑洞具有不同的微观结构㊂全息互信息测量了量子信息理论中2个子系统之间的相关性[1],可以通过计算连接一个永恒A d S 黑洞两侧的虫洞长度[2]获得全息互信息㊂热场二重态(t h e r m a l f i e l dd o u b l e s t a t e ,T F D )可以描述黑洞两侧纠缠态[3],即Ψ>ʉðie -β2E ii >L 췍i >R其中:β是温度的倒数;i >L 和i >R 是两侧的A d S 黑洞上相同的量子态㊂假设黑洞的每一侧存在2个完全相同的类空子区域A 和B ,则A 和B 之间的全息互信息I (A ,B )可以表示为[4]I (A ,B )ʉS (A )+S (B )-S (A ɣB )其中:S (A ),S (B )是最小表面A 和B 上类空区域的纠缠熵;S (A ɣB )是穿过事件视界连接A 和B 的区域的纠缠熵㊂1 非奇异H a y w a r d -A d S 黑洞的全息互信息非奇异H a y w a r d -A d S 黑洞[56]是爱因斯坦引力与携带磁荷的电磁场非线性耦合的解析解㊂在四维A d S 背景下的H a y w a r d -A d S 黑洞解[78]为d s 2=-f (r )d t 2+d r 2f (r)+r 2dΩ2(1)其中,d Ω2=d θ2+s i n 2θd φ2,度规函数为f (r )=1-2M r 2g 3+r3-Λ3r 2(2)式(2)中得到的参数g 与黑洞总磁荷Q m 有关,即Q m =g22α(3)α为自由积分常数㊂永恒黑洞有2个渐近的A d S 区域,其可以用2个相同的㊁无相互作用的共形场论[4]的T F D 来进行全息描述㊂为了方便计算,令左渐近边界上的子区域A 和右渐近边界上的B 完全相同,即A =B ㊂在四维背景下,将A d S 黑洞边界参数化为(x ,y )的二维空间㊂将子区域A 或B 看作一条带,其宽度为x ɪ(0,x 0),且沿y 方向延伸,长度为Y ,Y ʉ1㊂因此,子区A 的纠缠熵S (A )=R e g i o n A /4,其中R e g i o n A 是最小表面的面积,即R e g i o n A =ʏx 00d x r ᶄ21-2M r 2g 3+r3+r 2+r 2(4)其中,r ᶄ=d r /d x ㊂如果将等式(4)中的被积函数看作 拉格朗日函数 L ,定义一个与x 方向平移相关的守恒量为r3r 2+r ᶄ21-2M r 2g 3+r3+r 2=r 2m i n(5)r m i n 为r ᶄ=0时的转折点㊂根据其表面对称性,转折点位于x =x 0/2㊂根据守恒方程(5),x 0为x 0=ʏx 0d x =2ʏɕr m i n d r r 1-2M r 2g 3+r3r 21(r /r m i n )4-1(6)式(6)中的最小面积为R e g i o n A =2ʏɕr m i n d r 1-2M r 2g 3+r3+r 21(r /r m i n )4-1(7) 由于B 与A 相同,所以R e g i o n B 与R e g i o n A 也是相同的㊂通过黑洞视界连接区域A (左)和B (右)的最小表面面积为R e g i o n A ɣB ,对应的纠缠熵为S (A ɣB )965第6期 李慧玲,等:磁荷对H a y w a r d -A n t i -d eS i t t e r 黑洞的全息互信息的影响=R e g i o n A ɣB /4㊂两侧的总面积R e g i o n A ɣB 可表示为R e g i o n A ɣB =4ʏɕr hd r 11-2M r 2g 3+r3+r 2r (8) 根据全息互信息表达式I (A ,B )ʉS (A )+S (B )-S (A ɣB ),结合式(7)和式(8),得到I (g )=ʏɕr m i n d r r 1-2M r 2g 3+r3+r 211-(r m i n /r )4-ʏɕr hd rr1-2M r 2g 3+r3+r 2(9)此即H a y w a r d -A d S 黑洞的全息互信息㊂2 磁荷对全息互信息的影响要讨论静态A d S 背景下磁荷对全息互信息的影响,首先要研究非奇异H a yw a r d 黑洞的全息互信息与条带宽度的关系㊂将式(6)代入到式(8)中,得到条带的宽度x 0与全息互信息I (x 0,g )的关系I (x 0,g )=12x 0r 2m i n +ʏɕr m i nd rr 1-2M r 2g 3+r3+r 21-(r m i n/r )4-ʏɕr h d rr 1-2M r 2g 3+r3+r 2㊂(10) 当I (x 0,g )=0时全息互信息会消失㊂因此,可得到全息互信息消失时条带宽度的临界值x 0c 为x 0c =2r 2m i n ʏɕr h d r r1-2M r 2g 3+r3+r 2-ʏɕr m i nd rr 1-2M r 2g 3+r3+r 21-(r m i n/r )éëêêêùûúúú4(11)图1 条带的宽度x 0和转折点位置r m i n 之间的关系(令r h =1,g =0.4)F i g .1 T h e r e l a t i o n s h i p be t w e e n t h ew i d t hof t h e s t r i p a n d t h e l o c a t i o no f t h e t u r n i n gpo i n t 图2 全息互信息I (x 0,g )和转折点位置r m i n 之间的关系(令r h =1,g =0.4)F i g .2 T h e r e l a t i o n s h i p b e t w e e n h o l o g r a ph i cm u t u a l i n f o r m a t i o na n d t u r n i n gpo i n t l o c a t i o n 首先研究条带的宽度x 0对转折点位置r m i n 的影响㊂根据式(6)中条带宽度x 0与转折点位置r m i n 之间的关系,绘制如图1所示的图像㊂如图1所示,当r m i n ңr h 时,条带宽度x 0的积分发散,式(6)中所表现出的趋势与图1中的图像是一致的㊂r m i n 越大对应的条带宽度越小㊂由式(10)和式(11)可知,当r m i n ңr h 时2个边界上条带的宽度几乎是发散的,所以全息互信息也是发散的,这与在图2中所绘制的趋势也是一致的㊂发散条带的全息互信息也会是发散的㊂如图2所示,当r m i n ʈ1.269时,全息互信息消失㊂也就说明全息互信息消失存在一个临界值㊂结合图1和图2,发现全息互信息I (x 0,g )和条带宽度x 0之间也存在密切关系,从而作出图3进行进一步研究㊂在图3中,可以清晰地看出,当磁荷g 取不同值时,全息互信息I (x 0,g )消失的条带宽度临界值x 0c 是不同的㊂其数值结果为g =0.4时,x 0c ʈ1.77;g =0.6时,x 0c ʈ1.89;g =0.8时,x 0c ʈ2.15㊂磁荷g 越大,其临界宽度的值x 0c 也越大㊂且当全息互信息I (x 0,g )为某一值时,对应的磁荷g 不同㊂意味着磁荷g 也会对全息互信息I (x 0,g )产生重要影响㊂从图3中还发现全息互信息I (x 0,g )总是随着条带宽度x 0的增加而增加㊂可见2个渐近边界075沈阳师范大学学报(自然科学版) 第41卷上的子系统更大,纠缠也更大㊂(从上到下磁荷g 分别为g =0.4,g =0.6,g =0.8)图3 全息互信息I (x 0,g )和条带宽度x 0之间的关系F i g .3 T h e r e l a t i o n s h i p b e t w e e n h o l o g r a ph i cm u t u a l i n f o r m a t i o na n d s t r i pew i d t h (从上到下的曲线对应于r m i n 从1.18增加到1.21,步长为0.01)图4 全息互信息I (x 0,g )和磁荷g 之间的关系F i g .4 T h e r e l a t i o n s h i p b e t w e e n h o l o g r a ph i cm u t u a l i n f o r m a t i o na n dm a g n e t i c c h a r ge 接下来,研究非奇异H a y w a r d 黑洞的磁荷g 对全息互信息I (x 0,g )的影响㊂由图4可见,对于每条曲线,全息互信息随着磁荷的增加而减小㊂存在一个临界磁荷g c 使得全息互信息为零,此时对偶的子区域之间不存在纠缠㊂图4中的4条曲线从上到下对应r m i n 从1.18增加到1.21,步长为0.01㊂由此发现,当磁荷g 为固定值时,r m i n 越大,全息互信息I (x 0,g )越小㊂且由图1可知,r m i n 与条带宽度x 0有关,r m i n 越大,边界上的条带宽度x 0越小,图4中的结论与图2中的结果相一致㊂当条带宽度固定时,随着温度的升高,2条条带的全息互信息也会增加㊂条带的临界宽度x 0c 是使得互信息消失的宽度,即I (x 0c ,g )=0㊂在图4中,随着磁荷的增大,全息互信息单调递减㊂3 结 论对非奇异H a y w a r d -A d S 黑洞的全息互信息的研究表明:在静态情况下,当r m i n ңr h 时全息互信息是发散的,且随着条带宽度的增加而增加,说明2个渐进子系统更大则纠缠也更大;磁荷对全息互信息有直接影响,全息互信息会随着磁荷的增加而减小,当磁荷增加到临近值g c 时,I (x 0c ,g )=0,即全息互信息消失,可见磁荷对H a y w a r d 黑洞全息互信息产生重要影响㊂参考文献:[1]N I E L S E N M A ,C HU A N GI .Q u a n t u m c o m p u t a t i o na n d q u a n t u m i n f o r m a t i o n [J ].A m JP h y s ,2002,70(5):558559.[2]C A IR G ,Z E N G X X ,Z HA N G H Q.I n f l u e n c eo f i n h o m o g e n e i t i e so nh o l o g r a p h i cm u t u a l i n f o r m a t i o na n db u t t e r f l y e f f e c t [J ].JH i g hE n e r g y P h y s ,2017,2017(7):120.[3]MA L D A C E N AJ ,S U S S K I N DL .C o o l h o r i z o n s f o r e n t a n g l e db l a c kh o l e s [J ].F o r t s c h rP h y s ,2013,61(9):781811.[4]S H E N K E RS H ,S T A N F O R D D.B l a c kh o l e sa n dt h eb u t t e r f l y e f f e c t [J ].J H i g h E n e r g y P h y s ,2013,2014(3):125.[5]T O R R E S R.N o n s i n g u l a rb l a c kh o l e s ,t h ec o s m o l o g i c a l c o n s t a n t ,a n da s y m p t o t i cs a f e t y [J ].P h y sR e vD ,2017,95(12):124004.[6]Z E N G XX ,L I U X M ,L I U W B .H o l o g r a p h i c t h e r m a l i z a t i o nw i t h a c h e m i c a l p o t e n t i a l i nG a u s s -B o n n e t g r a v i t y [J ].J H i g hE n e r g y P h y s ,2014,2014(3):124.[7]Z E N G XX ,L I U W B .H o l o g r a p h i c t h e r m a l i z a t i o n i nG a u s s -B o n n e t g r a v i t y [J ].P h y sL e t t B ,2013,726(6):481487.[8]P A R KC .H o l o g r a p h i c r e n o r m a l i z a t i o n i nd e n s em e d i u m [J ].A d vH i g hE n e r g y P h ys ,2014,2014(9):565219.175第6期 李慧玲,等:磁荷对H a y w a r d -A n t i -d eS i t t e r 黑洞的全息互信息的影响。

Journ al of Sha ngha i Univ er sity (En glish Edition ),2006,10(3):215-218Article ID :1007 6417(2006)03 0215 04Entanglement of atoms in Tavis Cummings modelDONG Chuan hua (董传华), ZHANG Ya li (张亚利)Depar tm ent of Phy sics ,College of Scien ces ,Shan ghai Un iver sity ,Shan gha i 200444,P .R .ChinaReceived Sep.24,2004; Revised Ja n.7,2005DO NG Chuan hua,Prof.,E mail:chdong@ma Abstract Entanglem ent is used to measure correlation between separated subsystems.von Neumann entropy is used to study evolu tions of entanglement of atoms in processes of interaction between atoms with the field prepared in coherent state.The effects of field intensity and detuning on entanglement a re investiga ted.It is shown that the entanglement exhibited osc illations in its evolutions,their amplitudes and mean values decrease with inc reasing field intensity.Oscillation frequenc ies increase with detuning,but the maximum values a re almost independent of detuning.Key words entanglem ent,entangled state,Jaynes Cummings model.PACS 2001 42.50. P1 IntroductionSuperposition principle is one of the fundamentals in quantum m echanics.A two level atom may be in the ground state |0 ,the excited state |1 o r the superpo sition states C 0|0 +C 1|1 .The coefficients C 0and C 1are complex probability amplitudes of |0 and |1 respectively.For a system consisting of two atoms,the state of total system may be in the direct p roduct states |0,1 or |1,0 .Acco rding to the superposition principle,the total system may also be in the superpo sition states 1 2(C 0|0,1 +C 1|1,0 ).This kind of superposition states of multi particle is called entan gled state.Recently,people have devoted much attention to the applications of entangled states in quantum information,such as quantum teleporting [1,2],quantumcopying and cloning [3],quantum cryptography andquantum secret sharing [4],and quantum computation [5].Various schemes of preparing entangledstates have been proposed [6].The concept of entan gling has been generalized to the states of multi parti cle system,i .e .,G reenberger Ho rne Zeilinger states.Various methods of preparing G H Z states have alsobeen proposed [7,8].Entangling can be realized with non local correlation and entanglement is defined to measure the degree ofnon local correlation.Some definitions of entanglement have been given [9,10].Zuo and Xia have studied the evolution properties of three body entanglement of two identical two level atoms in the presence of fieldin vacuum [11].Rendell and Rajagopal have studied the entanglement of initially entangled mixed state in damped Jaynes Cummings model and found the timeevolutions of the concurrence lower bound [12].In this paper,we will use the partial entropy to study evolu tions of entanglement for two atoms in the presence of the field in coherent state with Tavis Cummings model.Effects of light intensity and the detunning on evolutions of entanglement are investigated.2 Definition of entanglementConsidering a system consisting of two atoms A and B,its entanglement (partial entropy entanglement)E is defined with von Neumann entropy,i .e .E =S ( A )=S ( B ),(1)where A and B are reduced density operators of at oms A and B.von Neumann entropy is a generalization of Shannon entropy in classic system to quantum sys tem,which describes the quantum co rrelation betweenthe sub systems [13].von Neumann entropy is defined asS ( )=-tr( log 2 ).(2)With Schmidt decomposition,the density operato rs of atoms A and B can be written in the fo rmA=tr B( A B)=mj=12j|j A A!j|,B=tr A( A B)=mj=1 2j|j B B!j|,(3)where m∀min{dim H A,dim H B},H A and H B are the Hilbert subspaces of atoms A and B,respectively. It follows that A and B have m non zero eigenvalues j(j=1-m).The relation between E and j isE=-mj=1j log2 j.(4)For two atoms in the entangled states| AB=C1|1,1 +C2|1,0 +C3|0,1+C4|0,0 ,(5) the eigenvalues of A(or B)arej=121-(-1)j1-4|C1C4-C2C3|2,j=1or2.(6)The partial entropy entanglement can be calculated as follows.E=-( 1log2 1+ 2log2 2).(7) 3 Entanglement of two atoms in TavisCummings modelConsidering a system consisting of two level atoms A and B,the ground state and excited state are denot ed|0 and|1 respectively.The light field is initially prepared in the coherent state|! =nf n|n ,where f n=exp(- n 2)!n n!and n is mean photon num ber.Two atoms are in the entangled state|(0) ato m=1 2(|0,1 +|1,0 ).(8) This entangled state is one of Bell bases,which is maximally entangled state with entanglement E=1. The state evolves from the initial state to|(t) at time t>0|(t) =C1(t)|1,1;n-1 +C2(t)|1,0;n+C3(t)|0,1;n +C4(t)|0,0;n+1 ,(9) where the coefficients C j(t)(j=1-4)are to be de termined.In the interaction picture,the Hamiltonian of the system consisting of two atoms and a field in Tavis Cummings model is,H I=g(a+S-e i∀t+S+a e-i∀t),(10)where∀=#-#0,#0is the transiting frequency of at oms and#is the f requency of field,S+=S(A)++S(B)+, S-=S(A)-+S(B)-,and S(j)#(j=A or B)are the transit ing operato rs of atom A(or B).Substituting the inter action Hamiltonian Eq.(10)and the state vector Eq.(9)into the Schr dinger equation and solving it using a standard p rocedure with the initial condition Eq.(8), the coefficients C j(t),(j=1∃4)in Eq.(9)can be obtained as follows.C1(t)=-2n gm1∃1-∀[ei(∃1-∀)t-1]+m2∃2-∀[ei(∃2-∀)t-1]+m3∃3-∀[ei(∃3-∀)t-1],C2(t)=C3(t)=m1e i∃1t+m2e i∃2t+m3e i∃3t,C4(t)=-2n+1gm1∃1+∀[ei(∃1+∀)t-1]+m2∃2+∀[ei(∃2+∀)t-1]+m3∃3+∀[ei(∃3+∀)t-1],(11)wherem1=f n2∃2∃3+2(2n+1)g2(∃1-∃2)(∃1-∃3),m2=f n2∃1∃3+2(2n+1)g2(∃2-∃1)(∃2-∃3),m3=f n2∃1∃2+2(2n+1)g2(∃3-∃1)(∃3-∃2)(12)and∃1=2r1 3cos%,∃2=2r1 3cos(%+2& 3),∃3=2r1 3cos(%+4& 3),(13) r=[2(2n+1)g2+∀2]3 27,%=1 3arccos(-∀g2 r).(14) In the case of∀=0,C j(t)can be reduced toC1(t)=-i2nf n g sin(∋n t) ∋n,C2(t)=C3(t)=2-1 2f n cos(∋n t),C4(t)=-i2(n+1)f n g sin(∋n t) ∋n,(15) where Rabi frequency is2∋n and.(16)216J our nal of Shan gha i Univer sityThe reduced density operator of atom A can beobtainedA = n(|C 1|2+|C 2|2)|1 !1|+(|C 3|2+|C 4|2)|0 !0|+(C *2C 4+C *1C 3)|0 !1| +(C 2C *4+C 1C *3)|1 !0|,(17)its eigenvalues are =0.5(1#1-(),(18)where(=4[ n (|C 1|2+|C 2|2) n(|C 3|2+|C 4|2)- n(C 1C *3+C 2C *4)2].(19)Using Eq.(7),the evolutions of entanglement can be obtained,which are shown in Fig.1for the case of resonance.The atoms A and B are prepared initially in Bell base |1,0 +|0,1 ,so the initial entanglement is 1.In the processes of interaction between the atoms and the field,the state of the system consisting of at oms A and B will deviate from this Bell base.In case of resonance,the states will evolve to the state | (t ) at a time t >0,which can be rewritten as | (t ) =1 2 nf n {cos (∋n t )(|1,0;n +|0,1;n ) -i sin (∋n t )[1-1 (2n +1)|1,1n -1+1+1 (2n +1)|0,0;n +1 ]}=1 2 n f n {cos (∋n t )(|1,0;n +|0,1;n ) -i sin (∋n t )[(|1,1;n -1 +|0,0;n +1 )-1 (4n +2)(|1,1;n -1 -|0,0;n +1 )+%]}.(20)It can be seen from Eq.(20)that the other two Bellbases |1,1 #|0,0 appear in atom field interaction.These Bell bases evolve according to cosine and sine with frequency ∋n that is different for various pho ton numbers n .Superposing these Bell bases form the os cillations of entanglement in evolution. In a weaker field ( n <4),the valley values of oscil lations rise obviously with increasing field intensity so that the mean values of entanglements in the oscil lations increase (see Fig.1(a)-(c)).In a stronger field ( n >4),the mean values of entanglements de crease rapidly (see Fig.1(d)and (e)),and the am plitudes shrink sharply with enhancing the field.When n =15,entanglement is maintained roughly constant inevolution.Thus,enhancing the field makes the atomsdetangle.This can be explained by the fact that thequantum co rrelation is weakened due to enhancing the interaction of two atoms with the field respectively in a stronger field.Fig.1 Entanglement of two atoms in the case of resonanc e((a) n =0.2,(b) n =1.0,(c) n =4.0,(d) n =9.0,(e) n =15.0)Evolution of entanglement in off resonance are shown in Fig.2(for weaker field, n =0.2)and Fig.3(for stronger field, n =9).From these figures,it can be seen that oscillation frequencies increase and the amplitudes shrink with increasing detuning in a weaker field.Except these oscillations,there are slow varia tions with large amplitudes in evolution for a stronger field and large detuning.The minimum values rise in a weaker field (see Fig.2)and drop in a stronger field (see Fig.3)with increasing the detuning.The maxi mum values of entanglement in the evolution are inde pendent of detuning almost,while dependent only on the field intensity.In summary,in interactions between atoms and the field,entanglements of two atoms will oscillate due to the Rabi oscillations.The field intensity and the detun ing affect evolutions of atom entanglement.Entanglements of two atoms depend on the field in tensity.The mean entanglem ents increase slightly in a weak field and decrease obviously in a strong field217Vol.10 No.3 Jun.2006DONG C H,et al .: Entanglem ent of atom s in Tavis Cummings modelFig.2 Entanglement of two atoms in the case of off resonanc efor n =0.2((a)∀=0.5g ,(b)∀=2.0g ,(c)∀=4.0g ,(d)∀=10.0g ,(e)∀=20.5g)Fig.3 Entanglement of two atoms in the case of off resonanc efor n =9.0((a)∀=0,(b)∀=0.5g ,(c )∀=1.0g ,(d)∀=4.0g ,(e)∀=10g )with increasing field intensity.It follows that a strong field makes the atoms detangle.The amplitudes of oscillations of entanglements shrink sharply with in creasing field intensity.The maximum values of entan glement are independent of detuning but dependent on the field intensity.The oscillation frequencies increase and the amplitudes shrink in a weak field with the increasing detuning.References[1] Bennett C H,Wiesner S munication v ia one andtwo particle operators on Einstein Podolsky Rosen states [J].Phys .Rev .Lett .,1992,69(20):2881-2884.[2] Bennett C H,Brassard G,Cr peau C,et al .Teleportingan unknown quantum state via dual classical and Ein stein Podolsky Rosen c hannels [J].Phy s .Rev .Lett .,1993,70(13):1895-1898.[3] Buzek V,H illery M.Quantum copying:Beyond the nocloning theorem[J].Phys .Rev .,1996,A54(3):1844-1852.[4] Hillery M,Buzek V,Berthiaume A.Quantum secret sharing[J].Phys .Rev .,1999,A59(3):1829-1834.[5] Anders S rensen,Klaus M lme r.Entanglement and quantum computation with ions in the therm al motion [J ].Phys .Rev .,2000,A 62(2):022311 1-022311 11.[6] Cirace J I,Zoller P.Preparation of macroscopic superposition in many atom systems [J ].Phy s .Rev .,1994,A50(4):R2799-R2802.[7] Yao C M,Guo G C.Generation of spin type G HZ statesof the cavity field in squeezed coherent states[J].Acta Phy sica Sinica ,2001,50(1):59-62(in Chinese).[8] Liu X,Li H C.Prepa ration of multi atom GHZ states v iathe Raman interaction of V type three level atoms and one cavity field[J].Acta Phy sica Sin ica ,2001,50(9):1689-1692(in Chinese).[9] Vedral V,Plenio M B,Rippin M A,et al .Quantifyingentanglement[J].Phys .Rev .Lett .,1997,78(12):2275-2279.[10] Vedral V,Plenio M B.Entanglement measures and purification procedures[J].Phy s .Rev .,1998,A57:1619-1633.[11] Zhou Z C,Xia Y J.The evolution property of three bodyentanglement measure in Tavis Cumm ings model [J ].Acta Physica Sinica ,2003,52(11):2687-2693(in Chinese).[12] Rendell R W,Rajagopal A K.Revivals and entanglementfrom initially entangled mixed sta tes of a damped Jaynes Cumm ings model [J].Phys .Rev .,2003,A67(6):062110 1-062110 11.[13] von Neumann.Mathem atical F oundat ion s of Qua ntumMechan ics [M].Princeton University Press,Princeton,NJ,1955.(Editor YAO Yu e yuan )218J our nal of Shan gha i Univer sity。

1. American RomanticismThe romantic period stretched from the end of the eighteenth century through the outbreak of the Civil War. It is a term that is associated with imagination and boundlessness, as contrasted with classicism, which is commonly associated with reason and restriction. A romantic attitude may be detected in literature of any period, but as an historical movement it arose in the 18th and 19th centuries, in reaction to more rational literary, philosophic, artistic, religious, and economic standards. The most clearly defined romantic literary movement in the U. S. was Transcendentalism."Characteristics of the romantic movement in American literature are sentimentalism, primitivism and the cult of the noble savage; political liberalism; the celebration of natural beauty and the simple life; introspection; the idealization of the common man, uncorrupted by civilization; interest in the picturesque past; interest in remote places; antiquarianism ; individualism; morbid melancholy; and historical romance.Tanscendentalism was a spiritual, philosophical and literary movement and is located in the history of American Thought as Post-Unitarian（一神教）and free thinking in religious spirituality, Kantian and idealistic in philosophy and romantic and individualistic in literature. New England T ranscendentalism was the product of a combination of foreign influences and the native American Puritan tradition. The most important American Transcendentalists are Ralph Waldo Emerson and Henry David Thoreau, whose representative works are Nature and Walden respectively. T ranscendentalists generally agreed that the intuitive faculty, instead of the rational or sensical, became the means for a conscious union of the individual psyche with the world psyche also known as the Oversoul, life-force, prime mover and God . The basic premises include: First, an individual is the spiritual center of the universe - and in an individual can be found the clue to nature, history and, ultimately, the cosmos itself;Second, the structure of the universe literally duplicates the structure of the individual self - all knowledge, therefore, begins with self-knowledge; Third, transcendentalists accepted the neo-Platonic conception of nature as a living mystery, full of signs - nature is symbolic; Fourth,The belief that individual virtue and happiness depend upon self-realization - this depends upon the reconciliation of two universal psychological tendencies: the expansive or self-transcending tendency and .the contracting or self-asserting tendency.2. Free verse：Free verse is a form of poetry that refrains from consistent meter patterns, rhyme, or any other musical pattern.Some poets have explained that free verse, despite its freedom, must still display some elements of form. Most free verse, for example, self-evidently continues to observe a convention of the poetic line in some sense, at least in written representations, thus retaining a potential degree of linkage, however nebulous （模糊的）, with more traditional forms. Donald Hall goes as far as to say that "the form of free verse is as binding and as liberating as the form of a rondeau（回旋诗）." and T. S. Eliot wrote, "No verse is free for the man who wants to do a good job."Some poets have considered free verse restrictive in its own way. Robert Frost later remarked that writing free verse was like "playing tennis without a net".Walt Whitman, who based his verse approach on the Bible, was the major precursor for modern poets writing free verse, though they were reluctant to acknowledge his influence.Form and Structure：Although free verse requires no meter, rhyme, or other traditional poetic techniques, a poet can still utilize them to create some sense of structure. A clear example of this can be found in Walt Whitman's poems, where he repeats certain phrases and uses commas to create both a rhythm and structure.Because of a lack of predetermined form, free verse poems have the potential to take truly unique shapes. The poet is given more license to express and, unrestrained by traditional bounds, has more control over the development of the poem. This could allow for a more spontaneous and essentially individualizing factor.3. American realismIn American literature, the term "realism" encompasses the period of time from the Civil War to the turn of the century during which William Dean Howells, Rebecca Harding Davis, Henry James, Mark Twain, an d others wrote fiction devoted to accurate representation and an exploration of American lives in various contexts.Characteristics：Renders reality closely and in comprehensive detail. Selective presentation of reality with an emphasis on verisimilitude （似真，逼真）, even at the expense of a well-made plotCharacter is more important than action and plot; complex ethical （伦理的）choices are often the subject.Characters appear in their real complexity of temperament （性情）and motive; they are in explicable (possible to explain) relation to nature, to each other, to their social class, to their own past.Class is important; the novel has traditionally served the interests and aspirations of an insurgent (rebellious) middle class. (See Ian Watt, The Rise of the Novel)Events will usually be plausible (credible 可信的). Realistic novels avoid the sensational （耸人听闻的，令人激动的）, dramatic elements of naturalistic novels and romances.Diction is natural vernacular (dialect), not heightened or poetic; tone may be comic, satiric, or matter-of-fact.Objectivity in presentation becomes increasingly important: overt （公然的）authorial comments or intrusions （闯入）diminish as the century progresses.4. .American modernismAmerican Modernism covered a wide variety of topics including race relations, gender roles, and sexuality. It reached its peak in America in the 1920s up to the 1940s. Celebrated Modernists include Ezra Pound, William Carlos Williams, F. Scott Fitzgerald, Ernest Hemingway and William Faulkner, and while largely regarded as a romantic poet, Walt Whitman is sometimes regarded as a pioneer of the modernist era in America.The Centers of Modernism：（1）Stylistic innovations - disruption of traditional syntax and form.（2）Artist's self-consciousness about questions of form and structure.（3）Obsession with primitive material and attitudes.（4）International perspective on cultural matters.Modern Attitudes：（1）The artist is generally less appreciated but more sensitive, even more heroic, than the average person.（2）The artist challenges tradition and reinvigorates it.（3）A breaking away from patterned responses and predictable forms.Contradictory Elements：（1）Democratic and e l itist.（2）Traditional and anti-tradition.（3）National jingoism （沙文主义）and provinci a lity（乡土观念）versus the celebration of international culture.（4）Puritan ical and repressive elements versus freer expression in sexual and political matters.Literary Achievements：（1）Dramatization of the plight of women.（2）Creation of a literature of the urban experience.（3）Continuation of the pastoral or rural spirit.（4）Continuation of regionalism （地方主义）and local color.5. Imagism （意象派）Imagism—A literary movement launched by British and American poets early in the 20th century that advocated the use of free verse, common speech patterns, and clear concrete images as a reaction to Victorian sentimentalism, superposition and juxtaposition of images (意象的叠加和并置).A literary movement in U.S. and English poetry characterized by the use of concrete language and figures of speech, modern subject matter, metrical freedom, and avoidance of romantic or mystical themes. It grew out of the Symbolist movement and was initially led by Ezra Pound, who, inspired by the criticism of T. E. Hulme (休姆,1883 – 1917), formulated its credo c. 1912; Hilda Doolittle (杜丽特尔)was also among the founders. Around 1914 Amy Lowell (艾米·洛威尔)largely took over leadership of the group. Imagism influenced the works of Conrad Aiken (康拉德·艾肯), T. S. Eliot, Marianne Moore (玛丽安·穆尔), D. H. Lawrence, Wallace Stevens (华莱士·史蒂文斯), and others.Flint summarizes the "few rules" of Imagism as follows:（1）Direct treatment of the "thing," whether subjective or objective.（2）To use absolutely no word that did not contrib ute to the p resentation.（3. As regarding rhythm: to compose in sequence of the musical phrase, not in sequence of a metronome （节拍器）。

高中英语科技前沿词汇单选题50题1. In the field of computer science, when we talk about data storage, "cloud computing" provides a ______ solution.A. revolutionaryB. traditionalC. limitedD. temporary答案：A。

本题考查词汇含义。

“revolutionary”意为“革命性的”，“cloud computing”（云计算）在数据存储方面提供的是一种革命性的解决方案。

“traditional”表示“传统的”，不符合云计算的特点。

“limited”指“有限的”，与云计算的强大存储能力不符。

“temporary”意思是“临时的”，也不符合云计算作为长期数据存储方式的特性。

2. The development of artificial intelligence requires advanced algorithms and powerful ______.A. processorsB. memoriesC. screensD. keyboards答案：A。

“processors”是“处理器”，人工智能的发展需要先进算法和强大的处理器。

“memories”是“内存”，内存并非发展人工智能的关键硬件。

“screens”是“屏幕”，对人工智能发展并非核心硬件。

“keyboards”是“键盘”，与人工智能发展所需的硬件无关。

3. In the era of big data, ______ plays a crucial role in extracting valuable information.A. data miningB. data hidingC. data deletingD. data adding答案：A。

“data mining”是“数据挖掘”，在大数据时代，数据挖掘在提取有价值信息方面起着关键作用。