六年级奥数天天练

学而思奥数网天天练（高难度）六年级答：答答：第一题：唐老鸭和米老师赛跑唐老鸭与米老鼠进行一万米赛跑，米老鼠的速度是每分钟125米，唐老鸭的速度是每分钟100米。

唐老鸭手中掌握一种迫使米老鼠倒退的电子遥控器，通过这种遥控器发出第n 次指令，米老鼠就以原来速度的n ×10%倒退一分钟，然后再按原来的速度继续前进。

如果唐老鸭想在比赛中获胜，那么它通过遥控器发出指令的次数至少是_____次。

第二题：乒乓球训练（逻辑）甲、乙、丙三人用擂台赛形式进行乒乓球训练，每局2人进行比赛，另1人当裁判．每一局的输方去当下一局的裁判，而由原来的裁判向胜者挑战．半天训练结束时，发现甲共打了15局，乙共打了21局，而丙共当裁判5局．那么整个训练中的第3局当裁判的是 ．第三题：应用题 我国某城市煤气收费规定：每月用量在8立方米或8立方米以下都一律收6.9元，用量超过8立方米的除交6.9元外，超过部分每立方米按一定费用交费，某饭店1月份煤气费是82.26元，8月份煤气费是40.02元，又知道8月份煤气用量相当于1月份的715，那么超过8立方米后，每立方米煤气应收多少元？第四题：图形面积 直角三角形ABC 的两直角边8cm AC =，6cm BC =，以AC 、BC 为边向形外分别作正方形ACDE 与BCFG ，再以AB 为边向上作正方形ABMN ，其中N 点落在DE 上，BM 交CF 于点T ．问：图中阴影部分(ANE ∆、NPD ∆与梯形BTFG )的总面积等于多少？TPN M F D答：答：学而思奥数网天天练（高难度）六年级第一题答案： 第n 次米倒退距离设唐需对米发x 次指令x 次共计唐老鸭时间是为使唐胜利，米在100min 内距离必须小于1000 尝试得至少13次 第二题答案：本题是一道逻辑推理要求较高的试题．首先应该确定比赛是在甲乙、乙丙、甲丙之间进行的．那么可以根据题目中三人打的总局数求出甲乙、乙丙、甲丙之间的比赛进行的局数．⑴丙当了5局裁判，则甲乙进行了5局； ⑵甲一共打了15局，则甲丙之间进行了15510-=局；⑶乙一共打了21局，则乙丙之间进行了21516-=局； 所以一共打的比赛是5101631++=局．此时根据已知条件无法求得第三局的裁判．但是，由于每局都有胜负，所以任意连续两局之间不可能是同样的对手搭配，就是说不可能出现上一局是甲乙，接下来的一局还是甲乙的情况，必然被别的对阵隔开．而总共31局比赛中，乙丙就进行了16局，剩下的甲乙、甲丙共进行了15局，所以类似于植树问题，一定是开始和结尾的两局都是第五题：图形如图，长方形ABCD 中，E 为AD 的中点，AF 与BE 、BD 分别交于G 、H ，OE 垂直AD 于E ，交AF 于O ，已知5AH cm =，3HF cm =，求AG ．A B C D E F G H O乙丙，中间被甲乙、甲丙隔开．所以可以知道第奇数局(第1、3、5、……局)的比赛是在乙丙之间进行的．那么，第三局的裁判应该是甲．第三题答案：根据题意可知，这两个月份都超出了8立方米，8月份交了6.9元加上40.02 6.933.12-=元，1月份交了6.9元加上82.26 6.975.36-=元，其中33.12元和75.36元是超出的部分．由于8月份煤气用量相当于1月份的715，可以把8月份煤气用量看作7份，1月份煤气用量看作15份．1月份比8月份多用了8份，多交了75.3633.1242.24-=元．所以这42.24元就对应8份，那么33.12元对应6933.1242.24811÷⨯=份，所以6.9元部分(8立方米)对应 69871111-=份，1份为881111÷=立方米．由于42.24元就对应8份，所以超过8立方米后，每立方米煤气应收42.24(118)0.48÷⨯=元．第四题答案：如右图，AB 是直角三角形ABC 的斜边． 所以2222228610AB AC BC =+=+=．即10cm AB =．设四边形ACPN 的面积为1S ，BTC ∆的面积为2S ，四边形CTMP 的面积为3S ．而根据勾股定理，有12S S ++S 阴影123ABC S S S S ∆=+++． 所以S 阴影3ABC S S ∆=+．而ABT PMB S S ∆∆=，即223ABC S S S S ∆+=+，所以3ABC S S ∆=． 所以S 阴影22286248cm ABC S ∆==⨯⨯÷=． 第五题答案：由于AB ∥DF ，利用相似三角形性质可以得到::5:3AB DF AH HF ==，又因为E 为AD 中点，那么有:1:2OE FD =， 所以3:5:10:32AB OE ==，利用相似三角形性质可以得到::10:3AG GO AB OE ==， 而()()11534cm 22AO AF ==⨯+=，所以()10404cm 1313AG =⨯=．。

学而思奥数网天天练周练习（六年级）姓名： 成绩：答：答：第二题：求面积右图中，ABCD 是边长为1的正方形，A ，E ，F ，G ，H 分别是四条边AB ，BC ，CD ，DA 的中点，计算图中红色八边形的面积。

第一题：阴影面积如右图，在以AB 为直径的半圆上取一点C ，分别以AC 和BC 为直径在△ABC 外作半圆AEC 和BFC ．当C 点在什么位置时，图中两个弯月型（阴影部分）AEC 和BFC 的面积和最大。

答：答：答：答：第三题：正方形 如图所示，ABCD 是一边长为4cm 的正方形，E 是AD 的中点，而F 是BC 的中点。

以C 为圆心、半径为4cm 的四分之一圆的圆弧交EF 于G ，以F 为圆心、半径为2cm 的四分之一圆的圆弧交EF 于H 点，若图中1S 和2S 两块面积之差为2π(cm )m n -（其中m 、n 为正整数），请问m n +之值为何？第四题：追击问题 如下图，甲从A 出发，不断往返于AB 之间行走。

乙从C 出发，沿C —E —F —D —C 围绕矩形不断行走。

甲的速度是5米/秒，乙的速度是4米/秒，甲从背后第一次追上乙的地点离D 点____________米。

AC=80米，CD=EF=120米，CE=DF=30米，DB=100米F E D C B A 第五题：平均数 有4个不同的数字共可组成18个不同的4位数．将这18个不同的4位数由小到大排成一排，其中第一个是一个完全平方数，倒数第二个也是完全平方数．那么这18个数的平均数是：_______．学而思奥数网天天练周练习 （六年级）第一题答案：解答：两弯月形面积＝2221111188822AC BC AB AB BC AC BC πππ⨯+⨯-⨯+⨯⨯=⨯⨯本题即AC ×BC 何时有最大值.因为222A C B C A B +=，当22AC BC =时，2222()AC BC AC BC ⨯=⨯有最大值，此时AC ×BC 有最大值，即AC BC =时，阴影面积最大.第二题答案：解答：如图，易知蓝边正方形面积为15，△ABD 面积为18，△BCD 面积为120， 所以△ABC 面积为11382040-=，可证AE ∶EB ＝1∶4，黄色三角形面积为△ABC 的19，等于1120，由此可得，所求八边形的面积是：111451206-⨯=. 至此，我们对各部分的面积都已计算出来，如下图所示.【又解】设O 为正方形中心（对角线交点），连接OE 、OF ，分别与AF 、BG 交于M 、N ，设AF 与EC 的交点为P ，连接OP ，△MOF 的面积为正方形面积的116，N 为OF 中点，△OPN 面积等于△FPN 面积，又△OPN 面积与△OPM 面积相等，所以△OPN 面积为△MOF 面积的13，为正方形面积的148，八边形面积等于△OPM 面积的8倍，为正方形面积的16.第三题答案：解答：（法1）2248FCDE S cm =⨯=，21444BCD S ππ=⨯⨯=扇形2(cm )，221=2=cm 4BFH S ππ⨯⨯扇形（）而12=4--8FCDE BCD BFH S S S S S ππ-=--扇形扇形3π8=-2(cm )，所以3m =，8n =，3811m n +=+=． （法2）如右上图，1S S +=BFEA BFH S S -扇形2422π48π⨯-⨯⨯÷=-2(cm )，1244444164ABCD BCD S S S S ππ+=-=⨯-⨯⨯÷=-扇形2(cm )，所以，12(8π)(164π)3π8S S -=---=-2(cm )，故3811m n +=+=．第四题答案：解答：若甲要从背后追上乙，只有甲从D C →时才有可能，且当甲到达D 时，在DC 上乙离D 的距离不能超过1201205424-÷⨯=米．而甲第一次以上述行走方向到达D 时，要用(80120100100)580+++÷=秒，以后每隔(80120100)25120++⨯÷=秒到达一次． 乙走一圈的距离为(12030)2300+⨯=米． 设当甲第x 次以上述行走方向到达D 时，乙在DC 上离D 的距离不超过24米． 由于此时甲共走了[80120(1)]x +-秒，所以乙走了4[80120(1)]x ⨯+-米，而乙走的路程比300米的整数倍多出来的部分在302120180⨯+=米和18024+=米之间，所以有4[80120(1)]x ⨯+-除以300的余数在180到204之间，即(480160)x -除以300的余数在180~204之间．即480x除以300的余数在40~64之间，也即180x除以300的余数在40~64之间．显然当2x=时，360300÷的余数为60，在40~64之间．这时，乙走了4[80120(21)]800⨯+⨯-=米，离D点800300218020-⨯-=米．那么当甲追上乙时离D点20(54)5100÷-⨯=米．第五题答案：解答：一般而言，4个不同的数字共可组成4 424P=个不同的4位数．如果只能组成18个不同的4位数，说明其中必有0，这样才会组成332118⨯⨯⨯=个不同的4位数．在这四个不同的数中，则设最小的数20a b c m=，倒数第二个则是2cb a n=，两数正好是一对反序数．根据完全平方数的特点，a、c两数必是1、4、5、6、9之中的两个，且b在a、c之间．可以分为以下4类：⑴当4c=时，在1024、1034中，只有1024为完全平方数，但4201不是；⑵当5c=时，在1025、1035、1045中没有完全平方数；⑶当6c=时，在1026、1036、1046、1056、4056中也没有完全平方数；⑷当9c=时，在形为109b的数中，只有2331089=，而2980199=，符合题意；在形为409b的数中，由于2633969=，2674489=，均不符合；在形为509b的数中，由于2735329=，不符合；在形为609b的数中，由于2775929=，不符合．所以，符合条件的数只能是由1、0、8、9四个数组成的四位数．求这18个数的和，有两种方法，一种是枚举法，另一种是概率法．概率法的大致思路如下：对于没有0的四位数a，b，c，d排列成互不相同的四位数时，共有24个数，每个数字在每个数位上出现的概率是一样的，所以，每个数字在每个数位上都出现2446÷=次．则总和为：()61111a b c d+++⨯⨯．而其中如果有一个数是0，则在此基础上，考虑0作首位的部分要排除．即为：()()()()061111631116444 a b c a b c a b c+++⨯⨯-++⨯÷⨯=++⨯所以，本题中18个数的总和为()1896444++⨯，所以，这18个数的平均数为()1896444186444++⨯÷=．。

六年级奥数天天练试题及答案周汇总（4.7-4.10）六年级奥数天天练试题及答案 4.7 1. 甲、乙两人分别从A、B两地同时相向而行，甲行了全程的，正好与乙相遇，已知甲每小时行4.5千米，乙行完全程要5.5小时，求A B两地相距多少千米？【解析】相遇时甲乙路程比为5:6,速度比为5:6,乙的速度为4.5=5.4 千米/小时。

A，B两地的路程为（千米）。

2. 甲、乙两车分别从A、B两地同时出发，相向而行，甲车每小时行56千米，乙车每小时行40千米。

当乙车行至全程的时，甲车已超过中点12千米，A、B两地相距多少千米？【解析】甲、乙速度比：56: 40=7: 5，甲、乙的路程比：7: 5。

乙车行全程的时，甲车走了，也就是过中点12千米，所以全程为千米。

六年级奥数天天练试题及答案4.8 3. 甲船在静水中的船速是10千米/时，乙船在静水中的船速是千米/时.两船同时从港出发逆流而上，水流速度是千米/时，乙船到港后立即返回.从出发到两船相遇用了小时，问：，两港相距多少千米？【解析】乙船逆水时候的速度（千米/时），甲船逆水时候的速度（千米/时），两船逆水速度比为：，所以乙船到港时甲船行了 .乙船顺水速度与甲船逆水速度比为：，乙船返回到两船相遇，乙船行了，所以甲船小时共行了，，两港相距（千米）.4.甲、乙二人分别从A、B 两地同时出发，相向而行，甲、乙的速度之比是 4 : 3，二人相遇后继续行进，甲到达B地和乙到达A地后都立即沿原路返回，已知二人第二次相遇的地点距第一次相遇的地点30千米，则A B两地相距多少千米？【解析】两个人同时出发相向而行，相遇时时间相等，路程比等于速度之比，即两个人相遇时所走过的路程比为4:3.第一次相遇时甲走了全程的4/7 ;第二次相遇时甲、乙两个人共走了3个全程，三个全程中甲走了个全程，与第一次相遇地点的距离为个全程. 所以A、B两地相距（千米）.[ 来源:学。

科。

网][来源:学科网ZXXK] 六年级奥数天天练试题及答案 4.9 [来源:学|科|网Z|X|X|K] 5. 甲、乙两车分别从、两地出发，相向而行。

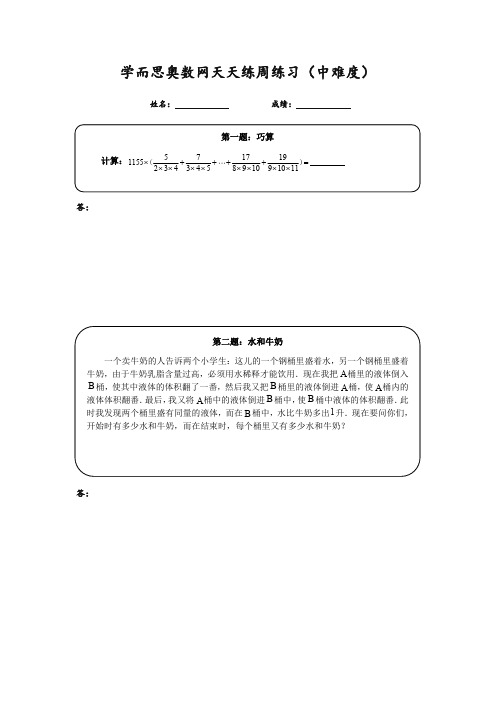
学而思奥数网天天练周练习（中难度）姓名：成绩：答：答：第一题：巧算计算：5717191155234345891091011⨯++++=⨯⨯⨯⨯⨯⨯⨯⨯（）第二题：水和牛奶一个卖牛奶的人告诉两个小学生：这儿的一个钢桶里盛着水，另一个钢桶里盛着牛奶，由于牛奶乳脂含量过高，必须用水稀释才能饮用．现在我把A桶里的液体倒入B桶，使其中液体的体积翻了一番，然后我又把B桶里的液体倒进A桶，使A桶内的液体体积翻番．最后，我又将A桶中的液体倒进B桶中，使B桶中液体的体积翻番．此时我发现两个桶里盛有同量的液体，而在B桶中，水比牛奶多出1升．现在要问你们，开始时有多少水和牛奶，而在结束时，每个桶里又有多少水和牛奶？答：答：第三题：浓度问题瓶中装有浓度为15%的酒精溶液1000克，现在又分别倒入100克和400克的A、B两种酒精溶液，瓶中的浓度变成了14%．已知A种酒精溶液浓度是B种酒精溶液浓度的2倍，那么A种酒精溶液的浓度是百分之几？第四题：灌水问题公园水池每周需换一次水．水池有甲、乙、丙三根进水管．第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时，恰好在打开某根进水管1小时后灌满空水池．第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时，灌满一池水比第一周少用了15分钟；第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时，比第一周多用了15分钟．第四周他三个管同时打开，灌满一池水用了2小时20分，第五周他只打开甲管，那么灌满一池水需用________小时．第五题：填数字请在下图的每个空格内填入1至8中的一个数字，使每行、每列、每条对角线上8个数字都互不相同．答：学而思奥数网天天练周练习（六年级）答案第一题答案：解答：本题的重点在于计算括号内的算式：571719234345891091011++++⨯⨯⨯⨯⨯⨯⨯⨯．这个算式不同于我们常见的分数裂项的地方在于每一项的分子依次成等差数列，而非常见的分子相同、或分子是分母的差或和的情况．所以应当对分子进行适当的变形，使之转化成我们熟悉的形式． 法一：观察可知523=+，734=+，……即每一项的分子都等于分母中前两个乘数的和，所以（法二）上面的方法是最直观的转化方法，但不是唯一的转化方法．由于分子成等差数列，而等差数列的通项公式为a nd +，其中d 为公差．如果能把分子变成这样的形式，再将a 与nd 分开，每一项都变成两个分数，接下来就可以裂项了．（法三）本题不对分子进行转化也是可以进行计算的：（法四）对于这类变化较多的式子，最基本的方法就是通项归纳．先找每一项的通项公式： 21(1)(2)n n a n n n +=++（2n =，3， (9)如果将分子21n +分成2n 和1，就是上面的法二；如果将分子分成n 和1n +，就是上面的法一．第二题答案：解答：假设一开始A 桶中有液体x 升，B 桶中有y 升．第一次将A 桶的液体倒入B 桶后，B 桶有液体2y 升，A 桶剩()x y -升；第二次将B 桶的液体倒入A 桶后，A 桶有液体2()x y -升，B 桶剩(3)y x -升；第三次将A 桶的液体倒入B 桶后，B 桶有液体(62)y x -升，A 桶剩(35)x y -升．由此时两桶的液体体积相等，得3562x y y x -=-，511x y =，:11:5x y =． 现在还不知道A 桶中装的是牛奶还是水，可以将稀释牛奶的过程列成下表：A 桶B 桶原A 桶液体：原B 桶液体 原A 桶液体：原B 桶液体初始状态 11:0 0:5 第一次A 桶倒入B 桶 6:0 5:5 第二次B 桶倒入A 桶 9:3 2:2 第三次A 桶倒入B 桶6:25:3由上表看出，最后B 桶中的液体，原A 桶液体与原B 桶液体的比是5:3，而题目中说“水比牛奶多1 升”，所以原A 桶中是水，原B 桶中是牛奶．因为在5:3中，“53-”相当于1升，所以2个单位相当于1升．由此得到，开始时，A 桶中有112升水，B 桶中有52升牛奶；结束时，A 桶中有3升水和1升牛奶，B 桶中有52升水和32升牛奶．第三题答案：解答：(法1)方程法．新倒入纯酒精：()100010040014%100015%60++⨯-⨯=(克)．设A 种酒精溶液的浓度为x ，则B 种为2x．根据新倒入的纯酒精量，可列方程： 100400602xx +⨯=，解得20%x =，即A 种酒精溶液的浓度是20%．(法2)浓度三角法．设A 种酒精溶液的浓度为x ，则B 种为2x．根据题意，假设先把100克A 种酒精和400克B 种酒精混合，得到500克的酒精溶液，再与1000克15%的酒精溶液混合，所以A 、B 两种酒精混合得到的酒精溶液的浓度为()100014%15%14%12%500--⨯=．根据浓度三角，有()12%:12%400:1002x x ⎛⎫--= ⎪⎝⎭，解得20%x =．故A 种酒精溶液的浓度是20%．第四题答案：解答：如第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时，恰好在打开丙管1小时后灌满空水池，则第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时，应在打开甲管1小时后灌满一池水．不合题意．如第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时，恰好在打开乙管1小时后灌满空水池，则第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时，应在打开丙管45分钟后灌满一池水；第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时，应在打开甲管后15分钟灌满一池水．比较第二周和第三周，发现开乙管1小时和丙管45分钟的进水量与开丙管、乙管各1小时加开甲管15分钟的进水量相同，矛盾．所以第一周是在开甲管1小时后灌满水池的．比较三周发现，甲管1小时的进水量与乙管45分钟的进水量相同，乙管30分钟的进水量与丙管1小时的进水量相同．三管单位时间内的进水量之比为3:4:2．第五题答案：解答：解此类数独题的关键在于观察那些位置较特殊的方格(对角线上的或者所在行、列空格比较少的)，选作突破口．本题可以选择两条对角线上的方格为突破口，因为它们同时涉及三条线，所受的限制最严，所能填的数的空间也就最小． 副对角线上面已经填了2，3，8，6四个数，剩下1，4，5和7，这是突破口．观察这四个格，发现左下角的格所在的行已经有5，所在的列已经有1和4，所以只能填7．然后，第六行第三列的格所在的行已经有5，所在的列已经有4，所以只能填1．第四行第五列的格所在的行和列都已经有5，所以只能填4，剩下右上角填5．再看主对角线，已经填了1和2，依次观察剩余的6个方格，发现第四行第四列的方格只能填7，因为第四行和第四列已经有了5，4，6，8，3．再看第五行第五列，已经有了4，8，3，5，所以只能填6． 此时似乎无法继续填主对角线的格子，但是，可观察空格较少的行列，例如第四列已经填了5个数，只剩下1，2，5，则很明显第六格填2，第八格填1，第三格填5．此时可以填主对角线的格子了，第三行第三列填8，第二行第二列填3，第六行第六列填4，第七行第七列填5．继续依次分析空格较少的行和列(例如依次第五列、第三行、第八行、第二列……)，可得出结果如下图．1346724578148627321567137865728635471288754321642431564835631852。

六年级奥数天天练试题及答案解析（31题）1·【题目】完全平方数【答案】2·【题目】数论综合【答案】3·【题目】数论综合【答案】4·【题目】数论综合【答案】5·【题目】数论综合【答案】6·【题目】枚举【答案】7·【题目】枚举【答案】8·【题目】枚举【答案】9·【题目】加乘原理【答案】10·【题目】加乘原理【答案】11·【题目】加乘原理【答案】12·【题目】排列组合【答案】13·【题目】排列组合【答案】14·【题目】排列组合【答案】15·【题目】数论综合【答案】16·【题目】排列组合【答案】17·【题目】排列组合【答案】【题目】图形计数【答案】19·【题目】图形计数【答案】20·【题目】图形计数【答案】21·【题目】图形计数【答案】22·【题目】计算与找规律【答案】23·【题目】计算与找规律【答案】24·【题目】计算与找规律【答案】25·【题目】计算与找规律【答案】26·【题目】计算与找规律【答案】27·【题目】几何模块【答案】28·【题目】几何模块【答案】29·【题目】几何模块【答案】30·【题目】几何模块【答案】31·【题目】行程模块【答案】。

六年级奥数天天练试题及答案8.29 【题目】【答案】六年级奥数天天练试题及答案8.30【题目】【答案】六年级奥数天天练试题及答案8.31 【题目】【答案】六年级奥数天天练试题及答案9.1 【题目】六年级奥数天天练试题及答案9.2 【题目】【答案】六年级奥数天天练试题及答案9.3 【题目】【答案】六年级奥数天天练试题及答案9.4 【题目】【答案】六年级奥数天天练试题及答案9.5 【题目】【答案】六年级奥数天天练试题及答案9.6【题目】【答案】六年级奥数天天练试题及答案9.7 【题目】【答案】六年级奥数天天练试题及答案9.8 【题目】【答案】六年级奥数天天练试题及答案9.9 【题目】【答案】六年级奥数天天练试题及答案9.10 【题目】【答案】六年级奥数天天练试题及答案9.11 【题目】【答案】六年级奥数天天练试题及答案9.12 【题目】【答案】六年级奥数天天练试题及答案9.13【题目】【答案】六年级奥数天天练试题及答案9.14 【题目】【答案】六年级奥数天天练试题及答案9.15 【题目】【答案】六年级奥数天天练试题及答案9.16【题目】【答案】六年级奥数天天练试题及答案9.17 【题目】【答案】六年级奥数天天练试题及答案9.19 【题目】【答案】六年级奥数天天练试题及答案9.20【题目】【答案】六年级奥数天天练试题及答案9.21 【题目】六年级奥数天天练试题及答案9.22 【题目】【答案】六年级奥数天天练试题及答案9.23【题目】【答案】六年级奥数天天练试题及答案9.24 【题目】【答案】六年级奥数天天练试题及答案9.25【题目】【答案】六年级奥数天天练试题及答案9.18 【题目】【答案】六年级奥数天天练试题及答案9.26 【题目】【答案】六年级奥数天天练试题及答案9.27【题目】【答案】六年级奥数天天练试题及答案9.28 【题目】【答案】六年级奥数天天练试题及答案9.29 【题目】【答案】六年级奥数天天练试题及答案9.30【题目】【答案】六年级奥数天天练试题及答案10.1 【题目】【答案】六年级奥数天天练试题及答案10.2 【题目】六年级奥数天天练试题及答案10.3 【题目】【答案】六年级奥数天天练试题及答案10.4【题目】【答案】六年级奥数天天练试题及答案10.5 【题目】六年级奥数天天练试题及答案10.6 【题目】【答案】六年级奥数天天练试题及答案10.7 【题目】【答案】六年级奥数天天练试题及答案10.8 【题目】【答案】六年级奥数天天练试题及答案10.10 【题目】【答案】六年级奥数天天练试题及答案10.11【题目】【答案】六年级奥数天天练试题及答案10.12 【题目】【答案】六年级奥数天天练试题及答案10.13 【题目】【答案】六年级奥数天天练试题及答案10.14【题目】【答案】六年级奥数天天练试题及答案10.15 【题目】【答案】六年级奥数天天练试题及答案10.16 【题目】【答案】三年级奥数天天练试题及答案10.31 【题目】【答案】三年级奥数天天练试题及答案11.1 【题目】【答案】三年级奥数天天练试题及答案11.2【题目】【答案】三年级奥数天天练试题及答案11.3 【题目】【答案】三年级奥数天天练试题及答案11.4【题目】【答案】三年级奥数天天练试题及答案11.5【题目】【答案】三年级奥数天天练试题及答案11.6【题目】【答案】六年级奥数天天练试题及答案10.31 【题目】【答案】六年级奥数天天练试题及答案11.1【题目】【答案】六年级奥数天天练试题及答案11.2 【题目】【答案】六年级奥数天天练试题及答案11.3 【题目】【答案】六年级奥数天天练试题及答案11.4 【题目】【答案】六年级奥数天天练试题及答案11.5 【题目】【答案】六年级奥数天天练试题及答案11.6 【题目】【答案】六年级奥数天天练试题及答案11.7 【题目】六年级奥数天天练试题及答案11.8【题目】【答案】六年级奥数天天练试题及答案11.9 【题目】【答案】六年级奥数天天练试题及答案11.10 【题目】【答案】六年级奥数天天练试题及答案11.11【题目】【答案】六年级奥数天天练试题及答案11.12 【题目】【答案】六年级奥数天天练试题及答案11.13 【题目】【答案】六年级奥数天天练试题及答案11.14 【题目】六年级奥数天天练试题及答案11.15【题目】【答案】六年级奥数天天练试题及答案11.16 【题目】【答案】六年级奥数天天练试题及答案11.17 【题目】【答案】六年级奥数天天练试题及答案11.18【题目】【答案】六年级奥数天天练试题及答案11.19 【题目】【答案】六年级奥数天天练试题及答案11.20 【题目】【答案】六年级奥数天天练试题及答案11.28 【题目】【答案】。

4.1（计算问题）【解析】4.2（计算问题）【解析】4.3（计算问题）【解析】4.4（计数）【答案】4.5（应用题）【答案】由于两次跑出羊后，剩下羊总数不变。

设剩下羊为[(9+7),(7+5)]=[16,12]=48份。

因此9:7=27:21，7:5=28:20，由于每次只跑一只羊，所以1份是1只，因此原来有1×48+1=49只羊。

所以这群羊原来有28+21=49只。

4.7（圆形跑道）答案】本题中，由于甲、乙两人在正常道路和泥泞道路上的速度都相同，可以发现，如果甲、乙各自绕着圆形跑道跑一圈，两人在正常道路和泥泞道路上所用的时间分别相同，那么两人所用的总时间也就相同，所以，两人同时出发，跑一圈后同时回到A点，即两人在A点迎面相遇，然后再从A点出发背向而行，可以发现，两人的行程是周期性的，且以一圈为周期．在第一个周期内，两人同时出发背行而行，所以在回到出发点前肯定有一次迎面相遇，这是两人第一次迎面相遇，然后回到出发点是第二次迎面相遇；然后再出发，又在同一个相遇点第三次相遇，再回到出发点是第四次相遇……可见奇数次相遇点都是途中相遇的地点，偶数次相遇点都是点．本题要求的是第99次迎面相遇的地点与点的距离，实际上要求的是第一次相遇点与点的距离．对于第一次相遇点的位置，需要分段进行考虑：由于在正常道路上的速度较快，所以甲从出发到跑完正常道路时，乙才跑了米，此时两人相距100米，且之间全是泥泞道路，此时两人速度相同，所以再各跑50米可以相遇．所以第一次相遇时乙跑了米，这就是第一次相遇点与点的距离，也是第99次迎面相遇的地点与点的距离．【答案】150米4.8（平行四边形）【答案】114.9（行程问题）【解析】4.10（流水行船）【解析】轮船顺流用3天，逆流用4天，说明轮船在静水中行4－3＝1（天），等于水流3＋4＝7（天），即船速是流速的7倍．所以轮船顺流行3天的路程等于水流3＋3×7＝24（天）的路程，即木筏从A城漂到B城需24天．4.11（火车过桥）【解析】根据另一个列车每小时走72千米，所以，它的速度为：72000÷3600＝20（米/秒）某列车的速度为：（250－210）÷（25－23）＝40÷2＝20（米/秒）某列车的车长为：20×25-250＝500-250＝250（米）两列车的错车时间为：（250＋150）÷（20＋20）＝400÷40＝10（秒）4.12（行程问题）【解析】假设每条边长为200厘米，则总时间=200÷50+200÷20+200÷40=4+10+5=19（分钟），爬行一周的平均速度=200×3÷19=（厘米/分钟）．4.14（数论综合）【答案】设这三个自然数为A，B，C，且A=×，B=×,C=×，当、、c均是质数时显然满足题意，为了使A，B，C的和最小，则质数、、应尽可能的取较小值，显然当、、为2、3、5时最小，有A=2×3=6,B=3×5=15，C=5×2=10．于是，满足这样的3个自然数的和的最小值是6+15+10=31．4.15（平均速度）【解析】4.16（龟兔赛跑）【解析】乌龟用时：5.2÷3×60=104（分钟）；兔子总共跑了：5.2÷20×60=15.6（分钟）．而我们有：15.6=1+2+3+4+5+0.6按照题目条件，从上式中我们可以知道兔子一共休息了5次，共15×5=75（分钟）．所以兔子共用时：15.6+75=90.6（分钟）．兔子先到达终点，比后到达终点的乌龟快：104-90.6=13.4（分钟）．4.17（追击问题）【解析】甲比乙多跑500米，应比乙多休息2次，即2分．在甲多休息的2分内，乙又跑了200米，所以在与甲跑步的相同时间里，甲比乙多跑500＋200＝700（米），甲跑步的时间为700÷（120－100）＝35（分）．共跑了120×35＝4200（米），中间休息了4200÷200－1＝20（次），即20分．所以甲第一次追上乙需35＋20＝55（分）．4.18（求速度）【解析】4.19（间隔发车）【解析】4.21（整除）【答案】首先这个数能被9整除，则其数字和是9的倍数而0＋1＋2＋3＋4＋5＋6=21=18＋3(=1＋2=0＋3)所以这5个数字只可能是:0，3，4，5，6或1，2，4，5，6中的一种由于a要尽可能小，先考察1，2，4，5，6，若不存在，再讨论0，3，4，5，6设这个5位数的形式为，研究它被27整除的余数10000a＋1000b＋100c＋10d＋e=(370×27＋10)a＋(37×27＋1)b＋(4×27－8)c＋10d＋e=27×(370a＋37b＋4c)＋10(a＋d)＋b＋e－8c则只要10(a＋d)＋b＋e－8c能被27整除，则能被27整除而10(a＋d)＋b＋e－8c=9(a＋d－c)＋(a＋b＋c ＋d＋e)这里a＋b＋c＋d＋e=18所以a＋d－c=－2，1，4为了使数值最小，首先考察a=1的情况此时d－c=－3，0，3显然d－c≠0对于d－c=±3，在同样的个数字时，d>c时这个5位数最小而d，c从2，4，5，6中满足d －c=3的只有5和2所以d=5，c=2余下的4和6分配给b和e所以b=4，e=6所以最小五位数是14256.4.22（行程问题）【解析】4.23（应用题）【解析】4.24（盈亏问题）【解析】我们知道从第二天起开始降价，先降价20%然后又降价24元，最终是按原价的56%出售的，所以一共降价44%，因而第三天降价24%。

小学奥数天天练（坚持打卡养成好习惯第一天）1、一片草地，每天都匀速长出青草，如果可供24头牛吃6天，20头牛吃10天，那么可供19头牛吃几天？【答案】：每天长草量：（20×10-24×6）÷（10-6）=14（份）原有草量：24×6-14×6=60（份）可吃天数：60÷（19-14）=12（天）小学奥数天天练（坚持打卡养成好习惯第二天）六年级有两个班，把（1）班人数的2/15调入（2）班，这时（2）班人数的3/5是（1）班人数的3/4，原来（1）班人数是全年级人数的几分之几?养成好习惯，做完再看答案哦调过后，（2)班与(1)班人数比是3/4:3/5=5:4，这时(1)班人数占两班总人数的4/(4+5)=4/9，可知没调之前(1)班人数占总人数的4/9÷(1-2/15)=20/39答：原来（1）班人数是全年级人数的20/39小学奥数天天练（坚持打卡养成好习惯第三天）有两个相同的正方体，每个正方体的六个面上分别标有数字1，2，3，4，5，6。

将两个正方体放在桌面上，向上的一面数字之和为偶数的有多少种情形？【解答】：要使两个数字之和为偶数，就需要这两个数字的奇、偶性相同，即两个数字同为奇数或偶数。

所以，需要分两大类来考虑：两个正方体向上一面同为奇数的共有3×3=9（种）不同的情形；两个正方体向上一面同为偶数的共有3×3=9（种）不同的情形；两个正方体向上一面同为偶数的共有3×3+3×3=18（种）不同的情形。

小学奥数天天练（坚持打卡养成好习惯第四天）某农场把61600公亩耕地划归为粮田与棉田，它们之间的比是7：2，棉田与其他作物面积的比6：1。

每种作物各是多少公亩？【解答】：粮田46200公亩，棉田13200公亩，其他作物2200公亩。

小学奥数天天练（坚持打卡养成好习惯第五天）现在有一堆苹果，第一天卖了全部苹果的3/5还多20千克，剩下的苹果占卖出苹果的11/19，求这堆苹果一共有多少千克？【解答】：600千克解析：设这堆苹果一共X千克，第一天卖了（3/5X+20）千克，剩下了（2/5X-20）千克2/5X-20=11/19（3/5X+20）。

六年级小学生奥数天天练1.六年级小学生奥数天天练篇一1、水果店里西瓜个数与白兰瓜个数的比为7：5。

如果每天卖白兰瓜40个，西瓜50个，若干天后，白兰瓜正好卖完，西瓜还剩36个。

水果店里原有西瓜多少个？【答案】设各运来7X和5X个（7X-36）/50=5X/404（7X-36）=5*5X28X-156=25X3X=156X=522、五年级上学期男、女生共有300人，这一学期男生增加1/25，女生增加1/ 20，共增加了13人。

这一学年六年级男、女生各有多少人？【答案】此题我们用假设来解答。

假设这一学期五年级男、女生人数都增加1/25，那么增加的人数应为300*1/ 25=12（人），这与实际增加的13人相差13-12=1（人）。

相差1人的原因是把女生增加的1/20看成1/25计算了，即少算了原女生人数的1/20-1/25=1/100，也就是说这1人正好相当于上学期女生人数的1%，可求出上学期女生的人数（13-300*1/25）÷（1/20-1/25）=100（人），男生人数为：300-100=200（人），这学年女生的人数：100*（1+1/20）=105人，这学年男生的人数：200*（1+1/25）=208（人）2.六年级小学生奥数天天练篇二1、某船往返于相距120千米的两港之间，顺水而下需用10小时，逆水而上需用15小时。

由于暴雨后水速增加，该船顺水而行只需8小时，那么逆水而行需要多少小时?【答案】在无风的时候，他跑100米要用12.5秒【解析】顺风时速度=90÷10=9(米/秒)，逆风时速度=70÷10=7(米/秒)无风时速度=(9+7)×1/2=8(米/秒)，无风时跑100米需要100÷8=12.5(秒)2、甲、乙二人分别从山顶和山脚同时出发，沿同一山道行进。

两人的上山速度都是20米/分，下山的速度都是30米/分。

甲到达山脚立即返回，乙到达山顶休息30分钟后返回，两人在距山顶480米处再次相遇。

天天练（高难度）六年级第一题：唐老鸭和米老师赛跑唐老鸭与米老鼠进行一万米赛跑，米老鼠的速度是每分钟125米，唐老鸭的速度是每分钟100米。

唐老鸭手中掌握一种迫使米老鼠倒退的电子遥控器，通过这种遥控器发出第n次指令，米老鼠就以原来速度的n×10%倒退一分钟，然后再按原来的速度继续前进。

如果唐老鸭想在比赛中获胜，那么它通过遥控器发出指令的次数至少是_____次。

答：答答：答：天天练（高难度）六年级第一题答案：第n次米倒退距离设唐需对米发x次指令x次共计唐老鸭时间是为使唐胜利，米在100min内距离必须小于1000尝试得至少13次第二题答案：本题是一道逻辑推理要求较高的试题．首先应该确定比赛是在甲乙、乙丙、甲丙之间进行的．那么可以根据题目中三人打的总局数求出甲乙、乙丙、甲丙之间的比赛进行的局数．⑴丙当了5局裁判，则甲乙进行了5局；⑵甲一共打了15局，则甲丙之间进行了15510-=局；⑶乙一共打了21局，则乙丙之间进行了21516-=局；所以一共打的比赛是5101631++=局．此时根据已知条件无法求得第三局的裁判．但是，由于每局都有胜负，所以任意连续两局之间不可能是同样的对手搭配，就是说不可能出现上一局是甲乙，接下来的一局还是甲乙的情况，必然被别的对阵隔开．而总共31局比赛中，乙丙就进行了16局，剩下的甲乙、甲丙共进行了15局，所以类似于植树问题，一定是开始和结尾的两局都是乙丙，中间被甲乙、甲丙隔开．所以可以知道第奇数局(第1、3、5、……局)的比赛是在乙丙之间进行的．那么，第三局的裁判应该是甲．第三题答案：根据题意可知，这两个月份都超出了8立方米，8月份交了6.9元加上40.02 6.933.12-=元，1月份交了6.9元加上82.26 6.975.36-=元，其中33.12元和75.36元是超出的部分．由于8月份煤气用量相当于1月份的715，可以把8月份煤气用量看作7份，1月份煤气用量看作15份．1月份比8月份多用了8份，多交了75.3633.1242.24-=元．所以这42.24元就对应8份，那么33.12元对应6933.1242.24811÷⨯=份，所以6.9元部分(8立方米)对应69871111-=份，1份为881111÷=立方米．由于42.24元就对应8份，所以超过8立方米后，每立方米煤气应收42.24(118)0.48÷⨯=元．第四题答案：如右图，AB是直角三角形ABC的斜边．所以2222228610AB AC BC=+=+=．即10cmAB=．设四边形ACPN的面积为1S，BTC∆的面积为2S，四边形CTMP的面积为3S．而根据勾股定理，有12S S++S阴影123ABCS S S S∆=+++．所以S阴影3ABCS S∆=+．而ABT PMBS S∆∆=，即223ABCS S S S∆+=+，所以3ABCS S∆=．所以S阴影22286248cmABCS∆==⨯⨯÷=．第五题答案：由于AB∥DF，利用相似三角形性质可以得到::5:3AB DF AH HF==，又因为E为AD中点，那么有:1:2OE FD=，所以3:5:10:32AB OE==，利用相似三角形性质可以得到::10:3AG GO AB OE==，而()()11534cm22AO AF==⨯+=，所以()10404cm1313AG=⨯=．。