设计洪峰流量计算
- 格式:doc
- 大小:129.50 KB
- 文档页数:3


洪峰流量计算8.7.3推理公式法计算设计洪峰流量推理公式法是基于暴雨形成洪水的基本原理推求设计洪水的一种方法。
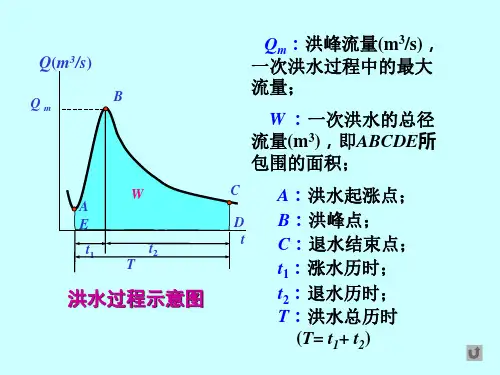
1.推理公式法的基本原理推理公式法计算设计洪峰流量是联解如下一组方程X便可求得设计洪峰流量Qp,即Qm,及相应的流域汇流时间τ。
计算中涉及三类共7个参数,即流域特征参数F、L、J;暴雨特征参数S、n;产汇流参数μ、m。
为了推求设计洪峰值,首先需要根据资料情况分别确定有关参数。
对于没有任何观测资料的流域,需查有关图集。
从公式可知,洪峰流量Qm和汇流时间τ互为隐函数,而径流系数ψ对于全面汇流和部分汇流公式又不同,因而需有试算法或图解法求解。
1. 试算法该法是以试算的方式联解式(8.7.4)(8.7.5)和(8.7.6),步骤如下:①通过对设计流域调查了解,结合水文手册及流域地形图,确定流域的几何特征值F、L、J,设计暴雨的统计参数(均值、C V、Cs / C V)及暴雨公式中的参数n(或n1、n2),损失参数μ及汇流参数m。
②计算设计暴雨的Sp、X TP,进而由损失参数μ计算设计净雨的T B、R B。
③将F、L、J、T B、R B、m代入式(8.7.4)(8.7.5)和(8.7.6),其中仅剩下Q m、τ、Rs,τ未知,但Rs,τ与τ有关,故可求解。
④用试算法求解。
先设一个Q m,代入式(8.7.6)得到一个相应的τ,将它与t c比较,判断属于何种汇流情况,再将该τ值代入式(8.7.4)或式(8.7.5),又求得一个Q m,若与假设的一致(误差不超过1%),则该Q m及τ即为所求;否则,另设Q m仿以上步骤试算,直到两式都能共同满足为止。
试算法计算框图如图8.7.1。
图8.7.1 推理公式法计算设计洪峰流量流程图2. 图解交点法该法是对(8.7.4)(8.7.5)和(8.7.6)分别作曲线Q m~τ及τ~ Q m,点绘在一张图上,如图8.7.2所示。
两线交点的读数显然同时满足式(8.7.4)(8.7.5)和(8.7.6),因此交点读数Q m、τ即为该方程组的解。


小流域洪峰流量计算的公式1、推理公式f Q n sm τψ278.0=当τ≥c t ,时,n su τψ-=1 当τc t ,时,nc t n -⎪⎭⎫ ⎝⎛=1τψn H s -=12424n--=410ψττ()nnnsF L mJ ----⎪⎪⎭⎫ ⎝⎛=414431410278.0τ()nc s n t 11⎥⎦⎤⎢⎣⎡-=μm Q ——设计频率的洪峰流量(m 3/s )ψ——洪峰径流系数τ——汇流历时(h)S ——暴雨雨力(mm/h)n ——暴雨衰减指数,其分界点为1小时,当t<1,取n=n 1,当t 1,取n=n 2μ——产流历时内流域内的平均入渗率(mm/h )c t ——产流历时24H ——设计频率的最大24小时雨量(mm )计算步骤1、根据地形图确定流域的特征参数F 、L 、J2、由公式4131FJ L =θ计算θ值,并根据相关公式计算汇流参数m3、由暴雨μ的参数等值线图确定设计流域的暴雨参数特征值24H 、C V 、C S 、n 1或n 2,并由皮尔逊Ⅲ型,结合频率查表,确定指定频率下的K p 值,由()241224H K s K S n p p p -== 4、有《四川省水文手册》,查出n-44的值,并根据ns m -⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=44410383.0θτ计算0τ值5、查表确定μ值,并计算n sτμ,查图由n 、n sτμ两坐标的焦点值,确定洪峰径流系数ψ6、根据《四川省水文手册》,查出n-41的值,计算流域汇流时间n--=41ψττ,计算τ值2、水利水电科学研究院的经验公式 适用于流域面积小于100km 2.32ksFQ m =洪峰流量参数K 可有下表3、公路科学研究所nm kFQ =指数n 为面积指数,当101≤≤F 时,K 值如下表梯形断面830)'(189.1⎥⎦⎤⎢⎣⎡-=i m m nQ h ,)1(2200m m h b -+=,212'm m +=。

1.1 3.4设计洪水3.4.1暴雨洪水特性鸭嘴河流域洪水主要由暴雨形成。
流域内暴雨一般出现在6~9月,且多连续降雨,受地形影响,降雨量不大。
据木里县气象站1970~2002年33年实测资料统计,最大一日降水量为77.4mm(1997年8月15日)、最大三日降水量111.6mm (1981年7月14日~16日)、最大五日降水量144.8mm(1981年7月14日~18日)。
鸭嘴河洪水出现时间与暴雨一致,洪水最早出现在5月,最迟出现在11月,但量级和强度较大的洪水一般出现在6~9月。
据邻近流域九龙河乌拉溪水文站1985~2004年20年实测资料统计,年最大流量最早出现在6月20日,最迟出现在9月4日,年最大洪水出现在6~7月的次数占全年的70%。
鸭嘴河流域的洪水具有峰不高、量较大、洪水历时长的特点。
一次洪水过程约2~3天,但洪水总量主要集中在一天。
鸭嘴站1990~1992年3年实测资料中,最大洪水发生在1991年,最大一日降水量58.5mm,洪峰流量为150m3/s,最大一日洪量1123万m3,三日洪量2809万m3,最大一日洪量占三日洪量的40%。
3.4.2设计洪水鸭嘴站仅有1990~1992年3年实测水文资料,且无法插补延长其洪水系列。
故采用推理公式法由设计暴雨推求布西水库设计洪水。
3.4.2.1布西水库坝址设计洪峰流量计算推理公式法洪峰流量计算公式:Q=0.278ψ(s/τn)F式中:Q——最大流量,m3/s;ψ——洪峰径流系数;s——暴雨雨力,mm/h;τ——流域汇流时间,h;n——暴雨公式指数;F——流域面积,km2。
(1)流域特征值在1/50000的地形图上,量算鸭嘴河布西水库坝址的流域特征值,见表3.7。
表3.7 鸭嘴河布西水库坝址流域特征值表(2)设计暴雨1)设计点雨量由于流域内缺乏短历时暴雨资料,本次蓄水安全鉴定各时段设计暴雨参数采用四川省水文局2006年出版的《四川省暴雨统计参数等值线图集》查算。

第二节设计洪峰流量及设计洪量的推求由流量资料推求设计洪峰及不同时段的设计洪量,可以使用数理统计方法,计算符合设计标准的数值,一般称为洪水频率计算。
一、资料审查在应用资料之前,首先要对原始水文资料进行审查,洪水资料必须可靠,具有必要的精度,而且,具备频率分析所必须的某些统计特性,例如洪水系列中各项洪水相互独立,且服从同一分布等。
除在第三章谈到审查资料的可靠性之外,还要审查资料的一致性和代表性。
为使洪水资料具有一致性,要在调查观测期中,洪水形成条件相同,当使用的洪水资料受人类活动如修建水工建筑物、整治河道等的影响有明显变化时,应进行还原计算,使洪水资料换算到天然状态的基础上。
洪水资料的代表性,反映在样本系列能否代表总体的统计特性,而洪水的总体又难获得。
一般认为,资料年限较长,并能包括大、中、小等各种洪水年份,则代表性较好。
此可见,通过古洪水研究,历史洪水调查,考证历史文献和系列插补延长等增加洪水列的信息量方法,是提高洪水系列代表性的基本途径。
根据我国现有水文观测资料情况,SL44—93规定坝址或其上下游具有较长期的实测水资料(一般需要30年以上),并有历史洪水调查和考证资料时,可用频率分析法计算计洪水。
二、样本选取河流上一年内要发生多次洪水,每次洪水具有不同历时的流量变化过程,如何从历洪水系列资料中选取表征洪水特征值的样本,是洪水频率计算的首要问题。
根据SL44—93规定,应采用年最大值原则选取洪水系列,即从资料中逐年选取一个大流量和固定时段的最大洪水总量,组成洪峰流量和洪量系列。
固定时段一般采用l、3、5、7、15、30天。
大流域、调洪能力大的工程,设计时段可以取得长一些;小流域、调洪能力小的工程,可以取得短一些。
在设计时段以内,还必须确定一些控制时段,即洪水过程对工程调洪后果起控制作用的时段,这些控制时段洪量应具有相同的设计频率。
同一年内所选取的控制时段洪量,可发生在同一次洪水中,也可不发生在同一次洪水中,关键是选取其最大值。

小流域洪峰流量计算的公式1、推理公式f Q n sm τψ278.0=当τ≥c t ,时,n su τψ-=1 当τc t ,时,nc t n -⎪⎭⎫ ⎝⎛=1τψn H s -=12424n--=410ψττ()nnnsF L mJ ----⎪⎪⎭⎫ ⎝⎛=414431410278.0τ()nc s n t 11⎥⎦⎤⎢⎣⎡-=μm Q ——设计频率的洪峰流量(m 3/s )ψ——洪峰径流系数τ——汇流历时(h)S ——暴雨雨力(mm/h)n ——暴雨衰减指数,其分界点为1小时,当t<1,取n=n 1,当t 1,取n=n 2μ——产流历时内流域内的平均入渗率(mm/h )c t ——产流历时24H ——设计频率的最大24小时雨量(mm )计算步骤1、根据地形图确定流域的特征参数F 、L 、J2、由公式4131FJ L =θ计算θ值,并根据相关公式计算汇流参数m3、由暴雨μ的参数等值线图确定设计流域的暴雨参数特征值24H 、C V 、C S 、n 1或n 2,并由皮尔逊Ⅲ型,结合频率查表,确定指定频率下的K p 值,由()241224H K s K S n p p p -== 4、有《四川省水文手册》,查出n-44的值,并根据ns m -⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=44410383.0θτ计算0τ值5、查表确定μ值,并计算n sτμ,查图由n 、n sτμ两坐标的焦点值,确定洪峰径流系数ψ6、根据《四川省水文手册》,查出n-41的值,计算流域汇流时间n--=41ψττ,计算τ值2、水利水电科学研究院的经验公式 适用于流域面积小于100km 2.32ksFQ m =洪峰流量参数K 可有下表3、公路科学研究所nm kFQ =指数n 为面积指数,当101≤≤F 时,K 值如下表梯形断面830)'(189.1⎥⎦⎤⎢⎣⎡-=i m m nQ h ,)1(2200m m h b -+=,212'm m +=。



洪峰流量的计算3.4设计洪⽔3.4.1暴⾬洪⽔特性鸭嘴河流域洪⽔主要由暴⾬形成。
流域内暴⾬⼀般出现在6~9⽉,且多连续降⾬,受地形影响,降⾬量不⼤。
据⽊⾥县⽓象站1970~2002年33年实测资料统计,最⼤⼀⽇降⽔量为77.4mm(1997年8⽉15⽇)、最⼤三⽇降⽔量111.6mm (1981年7⽉14⽇~16⽇)、最⼤五⽇降⽔量144.8mm(1981年7⽉14⽇~18⽇)。
鸭嘴河洪⽔出现时间与暴⾬⼀致,洪⽔最早出现在5⽉,最迟出现在11⽉,但量级和强度较⼤的洪⽔⼀般出现在6~9⽉。
据邻近流域九龙河乌拉溪⽔⽂站1985~2004年20年实测资料统计,年最⼤流量最早出现在6⽉20⽇,最迟出现在9⽉4⽇,年最⼤洪⽔出现在6~7⽉的次数占全年的70%。
鸭嘴河流域的洪⽔具有峰不⾼、量较⼤、洪⽔历时长的特点。
⼀次洪⽔过程约2~3天,但洪⽔总量主要集中在⼀天。
鸭嘴站1990~1992年3年实测资料中,最⼤洪⽔发⽣在1991年,最⼤⼀⽇降⽔量58.5mm,洪峰流量为150m3/s,最⼤⼀⽇洪量1123万m3,三⽇洪量2809万m3,最⼤⼀⽇洪量占三⽇洪量的40%。
3.4.2设计洪⽔鸭嘴站仅有1990~1992年3年实测⽔⽂资料,且⽆法插补延长其洪⽔系列。
故采⽤推理公式法由设计暴⾬推求布西⽔库设计洪⽔。
3.4.2.1布西⽔库坝址设计洪峰流量计算推理公式法洪峰流量计算公式:Q=0.278ψ(s/τn)F式中:Q——最⼤流量,m3/s;ψ——洪峰径流系数;s——暴⾬⾬⼒,mm/h;τ——流域汇流时间,h;n——暴⾬公式指数;F——流域⾯积,km2。
(1)流域特征值在1/50000的地形图上,量算鸭嘴河布西⽔库坝址的流域特征值,见表3.7。
表3.7 鸭嘴河布西⽔库坝址流域特征值表(2)设计暴⾬1)设计点⾬量由于流域内缺乏短历时暴⾬资料,本次蓄⽔安全鉴定各时段设计暴⾬参数采⽤四川省⽔⽂局2006年出版的《四川省暴⾬统计参数等值线图集》查算。
后河设计洪峰流量计算后河线路跨越断面处流域面积为F=1789.57km2,流域长度为L=78km,流域比降为J=2.64‰。
1 地区经验公式查《内蒙古自治区水文手册》得,C=3.64,n=0.55,Cv=1,Cs=2.5Cv,K p=1%=4.85,K p=2%=4.04,K p=20%=1.52。
Q m=CF n=3.64*1789.570.55=223.9m3/s。
Q1%= K p=1%* Q m=1086 m3/s;Q2%= K p=2%* Q m=905m3/s;Q20%= K p=20%* Q m=340m3/s;2 面积比法计算兴和水文站位于二道河上,位于线路跨越断面下游约20km,流域面积为F水文站=2019km2,其间有较大支流前河汇入。
2.1由兴和水文站实测流量计算根据收集兴和水文站1979年~2010年共32年实测历年最大洪峰流量系列,采用P-III型频率计算得,Q均=180,C V=1,Cs=2.5Cv;Q1%= K p=1%* Q m=872 m3/s;Q2%= K p=2%* Q m=729m3/s;Q20%= K p=20%* Q m=273m3/s;2.2 线路跨越处面积比法计算洪峰流量根据公式Q线1%=Q水文站(F线/F水文站)nQ1%=872*(1789.57/2019)0.55=816 m3/s;Q2%=729*(1789.57/2019)0.55=682 m3/s;Q20%=273*(1789.57/2019)0.55=255 m3/s;3 根据《内蒙古河流湖泊资料统计》计算得查《内蒙古河流湖泊资料统计》得知,根据兴和水文站采用1959~1960年和1963~1974年共14年实测最大洪峰流量计算得,Q均=239,C V=1,Cs=2.5Cv;Q1%=1160 m3/s;Q2% =966m3/s。
采用面积比法计算:Q线1%=Q水文站(F线/F水文站)nQ1%=1160*(1789.57/2019)0.55=1086 m3/s;Q2%=966*(1789.57/2019)0.55=904m3/s。
用EXCEL进行洪峰流量计算一、前言在水利工作中,经常需要计算设计洪水的洪峰流量,如水库的调洪演算、防洪堤的高度、拦沙坝的大小等等许许多多方面,都要知道洪峰流量的大小,推求洪峰流量一般有4种方法,一种是根据流量资料,通过频率的分析计算来求出设计洪水的洪峰流量;第二种是根据暴雨资料,通过频率计算求出设计暴雨,再通过流域的产流和汇流计算,推求出设计洪水的洪峰流量;第三种是经验公式法,利用简化的经验公式来估算设计洪水的洪峰流量;第四种是推理公式法。
在缺乏资料的小流域内,利用推理公式是推求洪峰量的主要方法。
由推理公式计算设计洪峰流量,需要计算三个方程:从以上的公式可看出,要求得洪峰流量Qm,必须求得Ψ和τ的值,而Ψ和τ互为参变,传统的方法是通过图解法和诺模图法求解,图解法需要画图,比较麻烦,诺模图法需要查图,容易出错,精度也不高。
还有没有快捷而又精准的方法呢答案是肯定的,这就是用EXCEL来计算洪峰流量。
EXCEL是我们常用的软件,其简洁的界面、丰富的函数、可编程的宏语言常常使我们事半功倍,工作轻松而更有效率。
下面就用推理公式法推求洪峰流量为例,介绍EXCEL在其中的应用。
二、计算方法为使叙述清晰易懂,下面以用编辑好的表格为例,介绍在EXCEL表格中用推理公式计算洪峰流量的方法。
见图1。
图1首先,在1至10行输入要用到的基本公式,目的是让人一目了然,了解计算的来龙去脉,也便于以后的理解。
@在14至18行输入基本数据,包括流域面积、河流长度、河道平均坡降、暴雨衰减指数、流域中心最大24小时降雨量,其中暴雨衰减指数和最大24小时降雨量可以从水文手册上查取,有条件的最好将之扫描下来,保存到表格文件的同一目录下,在计算表格中用超级链接将之链接起来,今后查算就十分方便了,再也不用东翻西找,鼠标一点超级链接就可查算。
第20至24行是计算雨力的值,最大24小时降雨量变差系数可由水文手册上查取,偏差系数一般采用变差系数的倍值,离均系数与设计频率有关,可查表计算,将离均系数表全部录入,放入另一张工作表中,见图2:图2我们一般常用的频率有5、10、20、30、50、100、200、300、500、1000年一遇,为实现离均系数自动查算,还需要动一番脑筋,离均系数表的横列为频率,纵列是Cs值,在离均系数表的N3和N4单元格中分别填入“=推理公式法!E21”、“=100/推理公式法!F22”,在N9单元格中填入:“=INDIRECT(ADDRESS(MATCH(INDIRECT(ADDRESS(3,14,)),A:A,1),MATCH(INDIRECT(AD DRESS(4,14,)),2:2,1)))+(INDIRECT(ADDRESS(MATCH(INDIRECT(ADDRESS(3,14,)),A:A,1)+ 1,MATCH(INDIRECT(ADDRESS(4,14,)),2:2,1)))-INDIRECT(ADDRESS(MATCH(INDIRECT(ADDRE SS(3,14,)),A:A,1),MATCH(INDIRECT(ADDRESS(4,14,)),2:2,1))))*(N3-INDIRECT(ADDRESS (MATCH(INDIRECT(ADDRESS(3,14,)),A:A,1),1)))/(INDIRECT(ADDRESS(MATCH(INDIRECT(AD DRESS(3,14,)),A:A,1)+1,1))-INDIRECT(ADDRESS(MATCH(INDIRECT(ADDRESS(3,14,)),A:A, 1),1)))”,这个算式的作用是用提供的频率和Cs值通过内插法得出离均系数的值,其中用到了INDIRECT、ADDRESS、MATCH三个函数,其用法可以参看EXCEL的帮助。