积分方程一般概念与弗雷德霍姆方程

积分方程的基础概念解析1. 积分方程简介积分方程是一种数学方程，其中未知函数出现在积分号内。

积分方程广泛应用于物理学、工程学、经济学和其他领域。

积分方程的一般形式为：K(x,y)+λf(x)=g(x)其中，K(x,y)是积分核，λ是参数，f(x)是未知函数，g(x)是已知函数。

2. 积分方程的分类积分方程根据积分核的不同，可以分为两类：•第一类积分方程：积分核只依赖于自变量x和y，与未知函数f(x)无关。

•第二类积分方程：积分核不仅依赖于自变量x和y，还依赖于未知函数f(x)。

3. 积分方程的求解方法积分方程的求解方法有很多种，常用的方法包括：•直接求解法：直接求解法是将积分方程化为一个代数方程或常微分方程，然后求解这个方程。

•迭代法：迭代法是一种数值求解方法，通过不断迭代来逼近积分方程的解。

•变分法：变分法是一种求解泛函极值的数学方法，也可以用来求解积分方程。

4. 积分方程的应用积分方程在物理学、工程学、经济学和其他领域有着广泛的应用，例如：•热传导问题：积分方程可以用来求解热传导方程。

•电磁学问题：积分方程可以用来求解电磁场方程。

•流体力学问题：积分方程可以用来求解流体力学方程。

•经济学问题：积分方程可以用来求解经济模型。

5. 积分方程的理论研究积分方程的理论研究是一个活跃的研究领域，目前已经取得了许多重要的进展。

积分方程的理论研究对积分方程的求解方法以及积分方程在各个领域的应用都有着重要的指导意义。

6. 结论积分方程是一种重要的数学方程，在物理学、工程学、经济学和其他领域有着广泛的应用。

积分方程的求解方法有很多种，常用的方法包括直接求解法、迭代法和变分法。

积分方程的理论研究是一个活跃的研究领域，目前已经取得了许多重要的进展。

积分方程的求解积分号下含有未知函数的方程称积为分方程的定义积分方程.积分的上下限均为常数弗雷德的积霍姆方程分方程.积分的上下限至少有一个含有变量的积伏特拉方程分方程.(1)f x 例连续函数满足方程10()(),x f x e x f t dt =+⎰2,t u t u ==，则解().f x 求1110002()()f t dt f u udu f u udu a ==⎰⎰⎰则，代入原方程，并记，()2xf x e ax =+，01x 等式两边同乘以，并从到做定积分，得11200()(2)xxf x dx xe ax dx =+⎰⎰，213a a =+计算得，3()6.xa f x e x ==+故，从而a(2)f x 例连续函数满足方程0()(),x xx e f x x e f t dt =-⎰0()()xy f t dt y f x '==⎰解令，则，().f x 求+xy y xe -'=，故通解为21[].2xdx dx x x y e xe e dx C Ce x e ----⎰⎰=+=+⎰由题意，21()2x x x f x Ce xe x e ---=-+-求导得，(0)00,C f ==，代入得21().2x x f x xe x e --=-故代入原方程，整理得()一阶线性微分方程(3)f x 已知为连续函数，且满例足积分方程0()sin ()(),x f x x x t f t dt =+-⎰00()sin ()(),x x f x x x f t dt tf t dt =+-⎰⎰原程可简解方化为().f x 求x 等式两边同时对求导，得0()cos ()x f x x f t dt '=+⎰，x 等式两边同时再对求导，得()sin ()f x x f x ''=-+，满足，(0)=0f ，(0)=1.f '(3)f x 已知为连续函数，且满例足积分方程0()sin ()(),x f x x x t f t dt =+-⎰().f x 求整理得()()sin .f x f x x ''-=-解得通解为：121()C +sin 2x x f x e C e x -=+，(0)=0(0)=1.f f '将，代入，得1211C =.44C =-，故111()+sin .442x x f x e e x -=-总结.本讲主要介绍两种简单的积分方程的求解方法。

积分方程知识点总结归纳一、积分方程的基本概念1. 积分方程的定义：积分方程是指自变量的函数与其导数之间的关系式，其中未知函数出现在积分式中。

2. 积分方程的类型：积分方程可以分为线性积分方程、非线性积分方程、微分-积分方程等多种类型。

3. 积分方程的一般形式：积分方程的一般形式可以表示为\[ \int{f(x,y,y')dx}=F(x,y,y')+C \]其中\(f(x,y,y')\)为给定函数，\(F(x,y,y')\)为未知函数，C为常数。

二、积分方程的解法1. 积分法：对积分方程进行积分，求解未知函数。

2. 变量代换法：通过合适的变量代换，将积分方程转化为更简单的形式进行求解。

3. 分离变量法：针对特定类型的积分方程，可以将方程中的变量分离在不同的方程中进行求解。

4. 特殊积分方程的解法：对于某些特殊形式的积分方程，如可分离变量、齐次积分等形式，可以采用特殊的解法进行求解。

三、积分方程的实际应用1. 物理问题：在物理学中，经常会遇到某些量的变化关系可以用积分方程描述，如经典力学、电磁学等。

2. 生物学问题：在生物学中，很多生物的生长、繁殖等过程可以用积分方程进行描述和分析。

3. 工程问题：在工程领域中，很多实际问题也可以转化为积分方程求解，如弹性力学、流体力学等。

4. 经济问题：在经济学中，也有很多问题可以用积分方程进行描述和求解，如经济增长模型、资源分配等。

四、积分方程的应用举例1. 弹簧振子问题：弹簧振子的运动可以用积分方程进行描述和求解，求得弹簧振子的位移和速度随时间的变化规律。

2. 人口增长问题：人口增长可以用积分方程进行描述，求解不同增长率下的人口变化规律。

3. 水桶倒水问题：水桶倒水的速度和水位变化可以用积分方程进行描述，求解不同倒水速率下的水位变化规律。

4. 物体自由落体问题：物体自由落体的速度和位移变化可以用积分方程进行描述，求解物体的运动规律。

计算机应用基础积分方程及应用常用文档在当今数字化的时代，计算机应用已经深入到我们生活和工作的方方面面。

其中，积分方程作为数学领域的一个重要分支，在计算机应用中也有着广泛而重要的应用。

本文将为您介绍计算机应用基础中的积分方程及其常见应用，帮助您更好地理解这一重要的数学工具。

一、积分方程的基本概念积分方程是指含有未知函数的积分式的方程。

它与微分方程一样，是数学物理方程中的重要类型。

积分方程可以分为线性积分方程和非线性积分方程。

线性积分方程又可以进一步分为第一类弗雷德霍姆积分方程、第二类弗雷德霍姆积分方程和沃尔泰拉积分方程。

第一类弗雷德霍姆积分方程的形式为：＼＼int_{a}＾｛b} K(x, t) ＼varphi(t) dt ＝ f(x)＼其中＼（K(x, t)＼）称为积分核，＼（＼varphi(t)＼）是未知函数，＼（f(x)＼）是已知函数。

第二类弗雷德霍姆积分方程的形式为：＼＼varphi(x) ＋＼lambda ＼int_{a}＾｛b} K(x, t) ＼varphi(t) dt ＝ f(x)＼沃尔泰拉积分方程与弗雷德霍姆积分方程的区别在于积分区间是可变的。

二、积分方程的求解方法求解积分方程的方法多种多样，常见的有数值解法和解析解法。

数值解法包括有限差分法、有限元法和蒙特卡罗方法等。

有限差分法是将积分方程转化为差分方程，通过迭代求解。

有限元法则是将求解区域划分为有限个单元，通过求解单元上的方程来逼近原方程的解。

蒙特卡罗方法则是基于随机抽样的思想来求解积分方程。

解析解法包括傅里叶变换法、拉普拉斯变换法等。

傅里叶变换法将积分方程在频域中进行求解，然后通过逆变换得到时域的解。

拉普拉斯变换法则是将积分方程在复频域中求解。

三、积分方程在计算机应用中的常见应用1、图像处理在图像处理中，积分方程常用于图像去噪、图像恢复和图像分割等方面。

例如，在图像去噪中，可以通过建立积分方程来描述图像的噪声模型，然后求解方程得到去噪后的图像。

第十五章 积分方程积分方程论是泛函分析的一个重要分支，它是研究数学其他学科（例如偏微分方程边值问题）和各种物理问题的一个重要数学工具。

本章叙述线性积分方程，重点介绍弗雷德霍姆积分方程的性质和解法；并简略地介绍了沃尔泰拉积分方程以及一些奇异积分方程；此外，还扼要地叙述积分方程的逐次逼近法和预解核，并举例说明近似解法；最后考察了一个非线性积分方程。

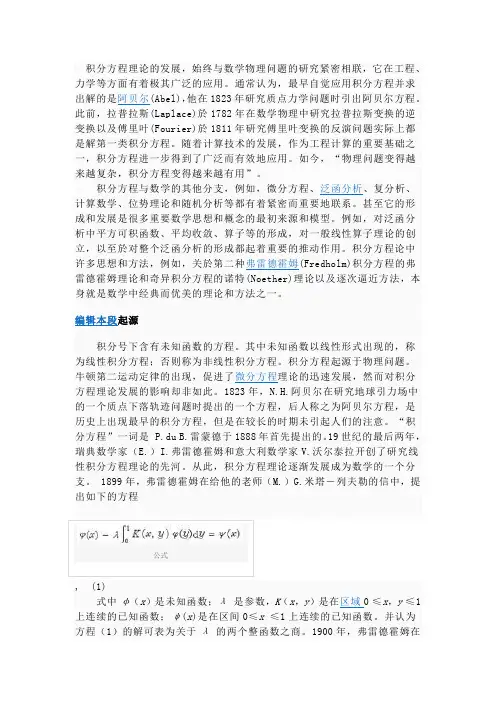
§1 积分方程一般概念与弗雷德霍姆方程一. 积分方程一般概念1. 积分方程的定义与分类[线形积分方程] 在积分号下包含未知函数y (x )的方程()()()()(),d ba x y x F x K x y αλξξξ=+⎰ (1)称为积分方程。

式中α(x ),F (x )和K (x,ξ)是已知函数，λ,a,b 是常数，变量x 和ξ可取区间(a,b )内的一切值；K (x,ξ)称为积分方程的核，F (x )称为自由项，λ称为方程的参数。

如果K (x,ξ)关于x,ξ是对称函数，就称方程(1)是具有对称核的积分方程；如果方程中的未知函数是一次的，就称为线性积分方程，方程(1)就是线性积分方程的一般形式；如果F (x )≡0 ，就称方程(1)为齐次积分方程，否则称为非齐次积分方程。

[一维弗雷德霍姆积分方程（Fr 方程）] 第一类Fr 方程()()(),d b aK x y F x ξξξ=⎰第二类Fr 方程()()()(),d bay x F x K x y λξξξ=+⎰第三类Fr 方程()()()()(),d bax y x F x K x y αλξξξ=+⎰[n 维弗雷德霍姆积分方程]111()()()()(),d DP y P F P K P P y P P α=+⎰称为n 维弗雷德霍姆积分方程，式中D 是n 维空间中的区域，P ,P 1∈D ，它们的坐标分别是(x 1,x 2, ,x n )和),,,(21n x x x ''' ,α(P )=α(x 1,x 2, ,x n ),F (P )=F (x 1,x 2, x n )和K (P ,P 1)=K (x 1,x 2, ,x n , ),,,21n x x x ''' 是已知函数，f (P )是未知函数。

弗雷德霍姆积分方程编辑词条分享形如(1)和(2)的积分方程，依次称为第一种弗雷德霍姆积分方程和第二种弗雷德霍姆积分方程，其中λ是参数，φ(x)是未知函数，核K(x，y)和自由项ƒ(x)是预先给定的函数。

通常假设K(x，y)属于平方绝对可积函数类，记,B是非负数。

当ƒ(x)恒为零时,称为齐次积分方程，否则称为非齐次积分方程。

逐次逼近法及解核第二种弗雷德霍姆积分方程的最简便的一种解法是逐次逼近法，即按递推公式给出方程(2)的n+1次近似解，这里K m(x,y)表示K(x,y)的m次叠核，即易知，，这里l可取为小于m的任何自然数。

当｜λ｜<B-1时,近似解序列{φn(x)}在【α,b】上是一致收敛的,其极限φ(x)就是方程(2)的解。

若级数一致收敛，记之为Γ(x,y;λ)，则Γ(x,y；λ)同时满足下面两个方程：,(3),(4)对于某值λ，若有平方绝对可积函数Γ(x，y；λ)同时适合方程(3)、(4),则称Γ(x,y；λ)为解核。

这时方程(2)对任意的自由项ƒ(x)有惟一解，它可表为,(5)反之亦然。

对于解核不存在的值λ，称为特征值。

否则，称为正则值。

当且仅当λ是特征值时，对应的齐次方程(6)才有非零解。

非零解φ(x)称为对应于λ的特征函数。

弗雷德霍姆方法 E.I.弗雷德霍姆给出了一般情形的解核构造法。

设K(x,y)是有界核,即│K(x,y)│<M（M是实常数），记,(7), (8)式中。

应用阿达马引理可估计,从而推知级数(7)、(8)对于一切复值λ是绝对一致收敛的，因此，D(λ)、D(x，y；λ)都是关于λ的整函数，并分别称为弗雷德霍姆行列式和弗雷德霍姆一阶子式。

可以证明，解核可表为Г(x,y；λ)=D(x，y；λ)/D(λ)。

这表明解核是λ的半纯函数。

同时，解核的极点都是D(λ)的零点，也都是齐次方程(6)的特征值。

反之亦然。

弗雷德霍姆定理弗雷德霍姆对于第二种积分方程的研究，可归结为如下的四个定理，总称为弗雷德霍姆定理。

第一篇积分方程第一章方程的导出和基本概念§1.1 方程的导出许多力学、工程技术和数学物理问题都能用积分方程形式描述，而求解常微分方程和偏微分方程的定解问题常常可转化为求解积分方程的问题。

下面举几个典型的问题作为例子，扼要地阐明导出积分方程的方法以及微分方程与积分方程之间的联系。

例1 ：弹性弦负荷问题一根轻且软的弹性弦，长为1,两端固定，如图所示，静止时与x轴重合, 弦内张力为T0 .今在其上加以强度为(x)的负荷.设在任一点M (横坐标为x)弦的位移y(x)已知.试确定(x),图i.i解：在任一点x 处取微小的一段弦d ,则作用于其上的重力为()d ,记之为F0,则这一重力F0必引起弦的形变，记处位移为S,则：T o sin i T o sin 2 F0,因为T o (x),所以1, 2 14 s •Ssin 1tan 1— ,sin 2S s所以T o - T o -一F0,得S P o (^^T o I•Ip记P 0引起的x 处位移为y (x), 则0 x 时,P)(l )T o Ix 1时‘七l1x,0 T o I I xT o I， 则 y (x) G(x, )P o ,y (x) G(x, ) ( )d对从o 到I 求积分, *y y (x) P)(l x)T o I记：G(x,)x x I.y(x) 0 G(x, ) ( )d .这就是负荷(X)满足的方程，是一个积分方程.例2 商场库存配送问题.商场销售某商品时,必须保持一定的库存总量A ,商场进货进入该商品后所进货物在时刻t 尚未售出概率为k(t).问商场应以什么样的速度(t )进货以保持稳定的库存量A.解开始营业时，库存为A,随后以速度(t)进货,考虑时刻t时的库存在任一小区间, d ] [0,t],d 时刻内进货为()d .到时刻t为止，这些货还剩k(t ) ( )d .所以时刻t 时,商品还剩：tAk(t) 0k(t ) ( )d .故tA Ak(t) 0k(t ) ( )d .例3 AbeI问题(等时线问题)一质点在重力作用下，在铅直平面自由地沿某曲线光滑地下滑，定此曲线的形状，以使此点从任一高度h 开始下滑到达x轴所用的时间为已知值f(h).图1.2y 解设此点落到任一高度，则 1mv 2mg(h y). 2v J2g(h y).记为过y 点的曲线的切线与x 轴夹 ddy J2g(h y) sindt v2g(h y) sindt 总hi 从0 h积分显然,定出曲线上任一点切线与 x 轴的夹角即相当于定出曲线.上式 可看成求曲线方程的积分方程 例4人口问题.记(y) 1 si(y) v2g(h y)dy f(h).设初始时人口总数为n0. f (t) 为生存函数,表示t 0 时出生的人到时刻t时的生存率，如图1.3所示.由于小孩出生,人口增加,设小孩出生率为(t). 此出生率与当时总人口数n(t)成正比，即(t) k n(t).取[0,t]任一微元区间[ ，d ] .则在此时段出生小孩为k n( ) d •到时刻t时，还存在的为f (t ) [k n( ) d ].故由于出生，到t时为止增加的人口为：t0 f(t ) k n( ) d .t 0时人口n o到时刻t还存在的为f (t)坯,得tn(t) n0 f(t) k 0 f(t ) n( )d例5偏微分方程的边值问题在寻求偏微分方程定解问题的解时，常常也可将方程和边界条 件包含在积分方程内，把解边值问 题化为求解积分方程问题。

积分方程理论的发展，始终与数学物理问题的研究紧密相联，它在工程、力学等方面有着极其广泛的应用。

通常认为，最早自觉应用积分方程并求出解的是阿贝尔(Abel)，他在1823年研究质点力学问题时引出阿贝尔方程。

此前，拉普拉斯(Laplace)於1782年在数学物理中研究拉普拉斯变换的逆变换以及傅里叶(Fourier)於1811年研究傅里叶变换的反演问题实际上都是解第一类积分方程。

随着计算技术的发展，作为工程计算的重要基础之一，积分方程进一步得到了广泛而有效地应用。

如今，“物理问题变得越来越复杂，积分方程变得越来越有用”。

积分方程与数学的其他分支，例如，微分方程、泛函分析、复分析、计算数学、位势理论和随机分析等都有着紧密而重要地联系。

甚至它的形成和发展是很多重要数学思想和概念的最初来源和模型。

例如，对泛函分析中平方可积函数、平均收敛、算子等的形成，对一般线性算子理论的创立，以至於对整个泛函分析的形成都起着重要的推动作用。

积分方程论中许多思想和方法，例如，关於第二种弗雷德霍姆(Fredholm)积分方程的弗雷德霍姆理论和奇异积分方程的诺特(Noether)理论以及逐次逼近方法，本身就是数学中经典而优美的理论和方法之一。

编辑本段起源积分号下含有未知函数的方程。

其中未知函数以线性形式出现的，称为线性积分方程；否则称为非线性积分方程。

积分方程起源于物理问题。

牛顿第二运动定律的出现，促进了微分方程理论的迅速发展，然而对积分方程理论发展的影响却非如此。

1823年，N.H.阿贝尔在研究地球引力场中的一个质点下落轨迹问题时提出的一个方程，后人称之为阿贝尔方程，是历史上出现最早的积分方程，但是在较长的时期未引起人们的注意。

“积分方程”一词是 P.du B.雷蒙德于1888年首先提出的。

19世纪的最后两年，瑞典数学家（E.）I.弗雷德霍姆和意大利数学家V.沃尔泰拉开创了研究线性积分方程理论的先河。

从此，积分方程理论逐渐发展成为数学的一个分支。

函数的积分变换与积分方程1. 引言在数学和应用数学中，函数的积分变换和积分方程是两个密切相关的概念。

积分变换是一种将函数从一个函数空间映射到另一个函数空间的算子，而积分方程则是一种求解未知函数的方程，其中未知函数出现在积分符号内或积分符号外。

2. 积分变换积分变换是一种将函数从一个函数空间映射到另一个函数空间的算子。

积分变换通常用于将一个复杂的函数变换成一个更简单的函数，以便于分析和求解。

常见的积分变换包括：•拉普拉斯变换•傅里叶变换•希尔伯特变换•梅林变换2.1 拉普拉斯变换拉普拉斯变换是一种将实变量函数变换成复变量函数的积分变换。

拉普拉斯变换广泛应用于电路分析、控制系统、信号处理等领域。

拉普拉斯变换的定义如下：∞F(s)=∫e−stf(t)dt其中，s是复变量，t是实变量，f(t)是实函数。

2.2 傅里叶变换傅里叶变换是一种将实变量函数变换成复变量函数的积分变换。

傅里叶变换广泛应用于信号处理、图像处理、量子力学等领域。

傅里叶变换的定义如下：∞F(ω)=∫e−iωtf(t)dt−∞其中，ω是复变量，t是实变量，f(t)是实函数。

3. 积分方程积分方程是一种求解未知函数的方程，其中未知函数出现在积分符号内或积分符号外。

积分方程通常用于求解微分方程、偏微分方程等。

常见的积分方程包括：•弗雷德霍姆积分方程•沃尔特拉积分方程•辛格积分方程3.1 弗雷德霍姆积分方程弗雷德霍姆积分方程是一种二阶线性积分方程，其形式如下：b(x,t)f(t)dtf(x)=g(x)+λ∫Ka其中，f(x)是未知函数，g(x)是已知函数，λ是常数，K(x,t)是核函数。

3.2 沃尔特拉积分方程沃尔特拉积分方程是一种一阶线性积分方程，其形式如下：x(x,t)f(t)dtf(x)=g(x)+λ∫Ka其中，f(x)是未知函数，g(x)是已知函数，λ是常数，K(x,t)是核函数。

4. 积分变换与积分方程的关系积分变换与积分方程之间存在着密切的关系。

数学中的积分方程积分方程是数学中重要而有趣的概念，它在不同领域的数学和应用中都有广泛的应用。

本文将介绍积分方程的定义、性质以及一些经典的应用领域。

一、积分方程的定义与形式积分方程是指方程中含有一个或多个未知函数的积分表达式。

一般来说，积分方程的形式可以表示为：f(x) = g(x) + λ∫[a,b] K(x,t) f(t) dt其中，f(x)是未知函数，g(x)是已知函数，λ是参数，K(x,t)是已知函数。

二、积分方程的类型根据积分方程中未知函数和积分变量的关系，积分方程可以分为几种类型：1. 调和积分方程：其中未知函数为调和函数，即满足拉普拉斯方程的函数。

调和积分方程在物理、工程等领域有广泛的应用。

2. 特殊函数积分方程：这类积分方程中的未知函数具有特殊函数特点，如Bessel函数、Legendre函数等。

这些特殊函数积分方程的解具有重要的数学和物理意义。

3. 直接积分方程：这类积分方程直接含有未知函数的积分项，常见的有Abel积分方程、Fredholm积分方程等。

这些方程的解可以通过迭代法或其他数值方法求解。

4. 间接积分方程：这类积分方程的未知函数出现在方程的内部，而不是直接作为积分变量。

这类方程的求解方法多种多样，常见的有Volterra积分方程、Hilbert积分方程等。

三、积分方程的性质积分方程具有许多有趣的性质，其中一些性质如下：1. 线性性质：积分方程是线性的，即满足线性叠加原理。

如果f1(x)和f2(x)是积分方程的解，那么f(x) = αf1(x) + βf2(x)也是积分方程的解，其中α和β是任意常数。

2. 解的存在性：对于一些特定的积分方程，解的存在性是有保证的。

例如，对于某些特殊函数积分方程，其有解的存在性得到了严格证明。

3. 解的唯一性：对于一些特殊形式的积分方程，解的唯一性也是可以保证的。

这些方程的解在一定的条件下是唯一的。

四、积分方程的应用积分方程在数学和应用中有广泛的应用，下面介绍几个经典的应用领域：1. 物理学中的应用：积分方程在电磁场、流体力学等领域中有着广泛的应用。

弗雷德霍姆积分方程弗雷德霍姆积分方程(FHIE)一类重要的方程，被广泛应用于科学研究和工程技术。

它主要用于描述系统的动态行为和研究过程，以及系统的行为变化。

这些方程通常可以建模出各种现象，如气流、流体力学、热传导、电磁场、结构动力学、声学等。

弗雷德霍姆积分方程由弗雷德霍姆(Fredholm)在1903年首先提出，并在1907年更进一步地普及与发展起来。

弗雷德霍姆积分方程的形式大体如下：右侧F(x)是已知的输入函数，它与其他参数无关；L(x)是已知的积分算子，它也与其他参数无关；g(x)是求解中需要计算的未知函数。

空间上，弗雷德霍姆积分方程可以描述为：在实际应用中，弗雷德霍姆积分方程用来求解各种实际问题，其中最重要的是静态和动态传递现象，包括物理量如温度、压力、速度、强度等。

这类积分方程可以用来描述大多数物理系统的时变行为，以此更好的模拟出物理系统的行为。

此外，弗雷德霍姆积分方程也可以用于几何学中的曲线拟合问题以及统计学中的密度估计等问题。

尤其在数学建模中，弗雷德霍姆积分方程常用于求解复杂的动态系统。

计算机技术的进步，为解决弗雷德霍姆积分方程带来了便利。

在数值分析领域，解决弗雷德霍姆积分方程有许多数值求解方法，比如时间步平均法、共轭梯度法等。

这些方法可以大大地缩短求解时间，提高系统的效率和准确性。

另外，也可以通过自适应网格技术和自适应步长技术来解决弗雷德霍姆积分方程，使得求解过程更加精确，并减少求解时间。

因此，计算机技术的发展，为解决弗雷德霍姆积分方程提供了更多有用的分析和计算方法。

综上所述，弗雷德霍姆积分方程是一种重要的方程，它能够有效地描述物理现象，在科学研究和工程技术中被广泛应用。

此外，计算机技术的进步为求解弗雷德霍姆积分方程提供了许多有用的分析和计算方法，为科技发展做出了重要贡献。

弗雷德霍姆积分方程弗雷德霍姆积分方程（Fredholm Integral Equation）是积分方程中的一种特殊形式，它是由瑞典数学家弗雷德霍姆（Ivar Fredholm）在19世纪末提出的。

以下将介绍弗雷德霍姆积分方程的定义、解析方法以及应用领域。

\[ \varphi(x) = f(x) + \lambda \int_a^b K(x, t) \varphi(t)dt \]其中，\(\varphi(x)\)是未知函数，\(f(x)\)是已知函数，\(\lambda\)是参数，\(K(x,t)\)是已知的核函数。

方程的解是通过求解未知函数\(\varphi(x)\)使得方程成立。

要解决在定义区间\([a,b]\)上的弗雷德霍姆积分方程，通常可以使用迭代法或特殊函数的展开方法。

一种常见的解法是迭代法。

大致思路如下：首先，将方程中的未知函数\(\varphi(x)\)进行分段展开，即将\([a, b]\)划分为若干个子区间，并在每个子区间上引入一组基函数，将\(\varphi(x)\)展开为这些基函数的线性组合。

这样，原方程可以转化为线性方程组的形式。

其次，将方程转化为矩阵方程，通过变换可以得到一个对角元素值为1的三角矩阵。

再次迭代求解方程，直到满足一定的收敛条件。

最后，将迭代得到的解向量进行合并，得到整个定义区间上的解。

另一种解法是利用特殊函数的展开方法。

例如，可以使用傅里叶级数展开、勒让德多项式展开等方法，将未知函数\(\varphi(x)\)在\[a, b\]上展开为一组特殊函数的级数。

通过比较系数，将级数展开的形式代入方程中，可以得到迭代求解方程的递推公式。

弗雷德霍姆积分方程在数学、物理、工程等领域都有广泛的应用。

例如，在控制论中，它可用于描述关于时间的状态转移方程、误差方程等。

在物理学中，弗雷德霍姆积分方程可用于描述电磁场的传播、光学中的散射问题等。

在工程应用中，它可用于信号处理、图像处理、声波传播等领域。

§1 积分方程一般概念与弗雷德霍姆方程一. 积分方程一般概念1. 积分方程的定义与分类[线形积分方程] 在积分号下包含未知函数y (x )的方程()()()()(),d ba x y x F x K x y αλξξξ=+⎰ (1)称为积分方程。

式中α(x ),F (x )和K (x,ξ)是已知函数，λ,a,b 是常数，变量x 和ξ可取区间(a,b )内的一切值；K (x,ξ)称为积分方程的核，F (x )称为自由项，λ称为方程的参数。

如果K (x,ξ)关于x,ξ是对称函数，就称方程(1)是具有对称核的积分方程；如果方程中的未知函数是一次的，就称为线性积分方程，方程(1)就是线性积分方程的一般形式；如果F (x )≡0 ，就称方程(1)为齐次积分方程，否则称为非齐次积分方程。

[一维弗雷德霍姆积分方程（Fr 方程）] 第一类Fr 方程()()(),d b aK x y F x ξξξ=⎰第二类Fr 方程()()()(),d bay x F x K x y λξξξ=+⎰第三类Fr 方程()()()()(),d bax y x F x K x y αλξξξ=+⎰[n 维弗雷德霍姆积分方程]111()()()()(),d DP y P F P K P P y P P α=+⎰称为n 维弗雷德霍姆积分方程，式中D 是n 维空间中的区域，P ,P 1∈D ，它们的坐标分别是(x 1,x 2, ,x n )和),,,(21n x x x ''' ,α(P )=α(x 1,x 2, ,x n ),F (P )=F (x 1,x 2, x n )和K (P ,P 1)=K (x 1,x 2, ,x n , ),,,21n x x x ''' 是已知函数，f (P )是未知函数。

关于Fr 方程的解法，一维和n (>1)维的情况完全类似，因此在以后的讨论中仅着重考虑一维Fr 方程。

一类函数积分方程的fredholm和非
fredholm定理
Fredholm和非Fredholm定理是定义在一类函数积分方程上的重要定理。

它们是由20世纪初著名的瑞典数学家阿尔维斯·弗雷德霍姆所发明的。

Fredholm定理指出，一类函数积分方程可以表示为linear integral equation。

在这种情况下， Fredholm定理给出了一个判别解决这类积分方程是否有解的规则：只有当Kernel K是要求的积分方程的解空间的可逆的半正定映射时，积分方程才能解决来。

常见的核函数类型包括简单对称structured，fualt-trigger symmettrical，特征向量对称和非对称。

而非Fredholm定理则指出，一类函数积分方程可以表示为非线性积分方程。

在这种情况下，非Fredholm定理给出了一个判别解决这类积分方程是否有解的规则：只有当Kernel F是函数方程的解空间的可逆的半正定映射时，积分方程才会有解。

例如，多项式形式积分方程的 method of variation of parameters (MVP)，椭圆形式函数积分方程的Chebychev分析和拉格朗日形式的函数积分方程的 Legendre 分析。

在拉格朗日形式函数积分方程中，还有一种特殊情况：由拉格朗日定理推出的非Fredholm定理，也称为Fourier-Stieltjes定理。

整体来看，Fredholm定理和非Fredholm定理是理解函数积分方程类型的重要工具，它们提供了一种有用的方法，可从积分方程中获得解。

因此，在计算函数积分方程时，Fredholm和非Fredholm定理都很有用。