绘制切割圆锥体的三视图Word版
- 格式:doc
- 大小:155.00 KB
- 文档页数:5
教学设计
•生产实际中有很多零件都是
圆柱体经过切割后形成的
书写课题:绘制圆柱切割体的三
视图并标注尺寸
•
提问:圆柱的三视图特征
一圆两方框都带细点画线
通过回答问题及观察动画
复习圆柱三视图的画法。
成的表面交线
(采用抢答的方式)
切火腿肠环节
提问:不同方向截平面对应截交线的形状
单一截平面圆柱体切割
提问不同方向截平面对应截交线在三视图中的投影情况。
对上台展示同学的作业进行点评示。
学生在上图的基础上进行绘画画出圆柱切割体的轮廓线并标注尺寸
教师讲解绘图的步骤及要求学生观察教师的绘图习题集P51。

教学过程:一、复习旧课1、圆锥体、圆柱体的投影分析和投影特征以及表面求点的方法。
二、引入新课题在曲面几次课我们学习了基本几何体的投影及表面求点,而在实际应用中,机器中的零件,往往不是基本几何体,而是基本几何体经过不同方式的截割或组合而成的。
三、教学内容(一)截交线的性质1、截交线的概念平面与立体表面相交,可以认为是立体被平面截切,此平面通常称为截平面,截平面与立体表面的交线称为截交线。
图3-12为平面与立体表面相交示例。
图3—12平面与立体表面相交2、截交线的性质(1)截交线一定是一个封闭的平面图形。
(2)截交线既在截平面上,又在立体表面上,截交线是截平面和立体表面的共有线。
截交线上的点都是截平面与立体表面上的共有点。
因为截交线是截平面与立体表面的共有线,所以求作截交线的实质,就是求出截平面与立体表面的共有点。
(二)平面与平面立体相交平面立体的表面是平面图形,因此平面与平面立体的截交线为封闭的平面多边形。
多边形的各个顶点是截平面与立体的棱线或底边的交点,多边形的各条边是截平面与平面立体表面的交线。
通过例题讲解平面立体截交线的画法。
1、讲解例题(例3-1)如图3-13(a)所示,求作正垂面P斜切正四棱锥的截交线。
分析:截平面与棱锥的四条棱线相交,可判定截交线是四边形,其四个顶点分别是四条棱线与截平面的交点。
因此,只要求出截交线的四个顶点在各投影面上的投影,然后依次连接顶点的同名投影,即得截交线得投影。
(a)(b)图3-13 四棱锥的截交线边画图边讲解作图方法与步骤。
当用两个以上平面截切平面立体时,在立体上会出现切口、凹槽或穿孔等。
作图时,只要作出各个截平面与平面立体的截交线,并画出各截平面之间得交线,就可作出这些平面立体的投影。
2、讲解例题(例3-2)如图3-14(a)所示,一带切口得正三棱锥,已知它的正面投影,求其另两面投影。
分析:该正三棱锥的切口是由两个相交的截平面切割而形成。
两个截平面一个是水平面,一个是正垂面,它们都垂直于正面,因此切口的正面投影具有积聚性。

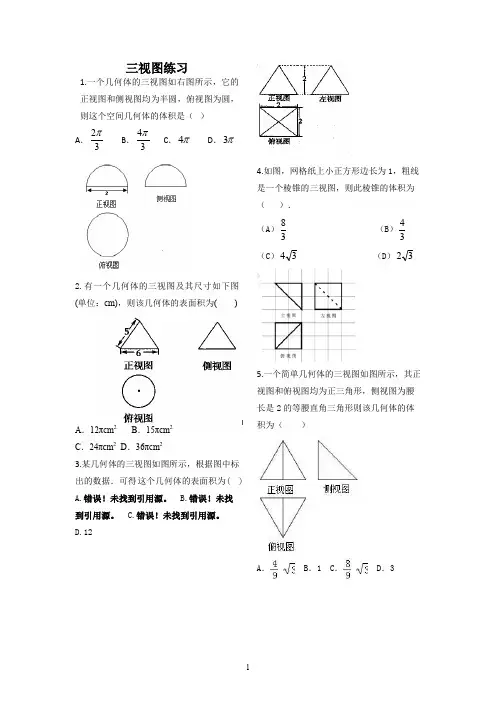
三视图练习1.一个几何体的三视图如右图所示,它的正视图和侧视图均为半圆,俯视图为圆,则这个空间几何体的体积是( ) A .32π B .34π C .π4 D .π32.有一个几何体的三视图及其尺寸如下图(单位:cm),则该几何体的表面积为( )A .12πcm 2B .15πcm 2C .24πcm 2D .36πcm 23.某几何体的三视图如图所示,根据图中标出的数据.可得这个几何体的表面积为( )A.错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D.124.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的体积为( ). (A )38 (B )34(C )34 (D)325.一个简单几何体的三视图如图所示,其正视图和俯视图均为正三角形,侧视图为腰长是2的等腰直角三角形则该几何体的体积为( )A .B .1C .D .36.某几何体的三视图如图所示(单位:cm ),则该几何体的侧面PAB 的面积是( ) A .7B .2C .1D .37.说出下列三视图(依次为主视图、左视图、俯视图)表示的几何体是( )A .六棱柱B .六棱锥C .六棱台D .六边形8.一个空间几何体的三视图如图所示,则该几何体的体积为( )A .56πcm 3 B .3πcm 3 B .C .32πcm 3 D .37πcm 3 9.右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( ) (A)9π (B )10π (C)11π (D)12π10.用若干单位正方体搭一个几何体,使它的正视图和俯视图如图所示,则它的体积的最大值和最小值分别为( )A. 9,14B.7,13C. 8,14D. 9,13 11.已知某几何体的三视图如上图所示,其中正视图,侧视图均是由三角形与半圆构成,视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( ) (A)2132π+(B)4136π+ (C)132+(D) 166+12.一个几何体的三视图如图所示,则该几何体的体积为( )(A)92 (B)72(C)3 (D)4 13.右图是一个几何体的三视图,根据图中数据,可得该几何体的体积是( )(A) 9π (B)1333π- (C )103π (D)133π 14.一个几何体的三视图如图所示,则该几何体的体积是( ) (A )64 (B )72 (C )80(D )11215.一个几何体的三视图如图所示,则该几何体的体积是( )A .64B .72C .80D .11216.已知一个几何体的三视图如下图所示(单位:cm),其中正视图是直角梯形,侧视图和俯视图都是矩形,则这个几何体的体积是________cm 3.17.如图为一个几何体的三视图,其中俯视为正三角形,A 1B 1=2,AA 1=4,则该几何体的表面积为_______。


任务一绘制切割体的三视图学习目标巩固三视图相关知识;知道截断体,掌握截交线。
能熟练运用表面取点法求解截交线。
任务分析图1—1 顶尖立体图如图1—1所示的顶尖,基本形状由大圆柱、小圆柱和圆锥三部分叠加,经切割而成,其轮廓线既包括基本体形状图线,也包括截交线。
这样的立体在现实生活中很多,要绘制这类立体的三视图,除了必备前面所学的三视图知识,还得学会截交线求作方法,综合运用才能绘制这类立体的三视图。
知识拓展一、截交线被截断后的基本几何体称为截断体,用来截断几何体的平面称为截平面,截平面与立体表面的交线称为截交线,截交线是封闭的曲线,由截交线围成的平面图形称为截面。
(一)平面体的截交线平面与平面体相交(平面体被截断),所得的交线是由直线组成的封闭多边形,该多边形的边就是平面体表面与截平面的交线,其顶点是棱线与截平面的交点。
求平面体的截交线,关键是找到截平面与立体棱线的共有点(截平面与立体各棱线的交点),然后将各点连接即为所求。
[例1—1] 如图1—2所示为一四棱柱被一正垂面截切,求截交线。
图1—2 四棱柱的截交线分析:四棱柱被截切,上底有两条边被截切,侧面有三条棱被截切,共有5条棱被截切,产生五个交点,截面为五边形。
此题的关键就是求作A、B、C、D、E五个顶点的投影。
先在主视图中标注出这些点,按投影关系在俯视图中找到对应的点,再按投影规律作出这些点的左视图投影,然后连接即为所求。
注意:1.要判别图线的可见性。
2.若立体被两相交平面截断,两截平面相交处有交线(交点在立体表面上),切不可漏画。
如图1—3所示。
图1—3 截切后的三棱柱(二)回转体的截交线1.圆柱的截断圆柱被截切后产生的截交线,因平面与圆柱轴线的相对位置不同而不同,可以分为三种情况,见表1—1所示。
表1—1 平面截切圆柱的截交线截平面位置平行于轴线垂直于轴线倾斜于轴线截交线矩形圆椭圆轴测图投影图[例1—2] 求圆柱被一正垂面截切后的截交线。
如图1—4。


北师大版七年级数学上册知识点总结(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(北师大版七年级数学上册知识点总结(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为北师大版七年级数学上册知识点总结(word版可编辑修改)的全部内容。
3、棱柱及其有关概念:棱:在棱柱中,任何相邻两个面的交线,都叫做棱。
侧棱:相邻两个侧面的交线叫做侧棱。
n 棱柱有两个底面,n 个侧面,共(n+2)个面;3n 条棱,n 条侧棱;2n 个顶点.4、正方体的平面展开图:11种总结规律:一线不过四,田凹应弃之;相间、Z 端是对面,间二、拐角邻面知。
5、截一个正方体:用一个平面去截一个正方体,截出的面可能是三角形,四边形,五边形,六边形。
可能出现的:锐角三角型、等边、等腰三角形, 正方形、矩形、非矩形的平行四边形、 非等腰梯形、 等腰梯形、五边形、六边形、正六边形不可能出现:钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边形3—3型2—2—2型6、三视图物体的三视图指主视图、俯视图、左视图。
主视图:从正面看到的图,叫做主视图。
左视图:从左面看到的图,叫做左视图。
俯视图:从上面看到的图,叫做俯视图。
第一章丰富的图形世界一、填空题(每空2分,共36分):1、圆锥是由________个面围成,其中________个平面,________个曲面.2、在棱柱中,任何相邻的两个面的交线都叫做______,相邻的两个侧面的交线叫做_______。
3、从一个多边形的某个顶点出发,分别连接这个点和其余各顶点,可以把这个多边形分割成十个三角形,则这个多边形的边数为_____。
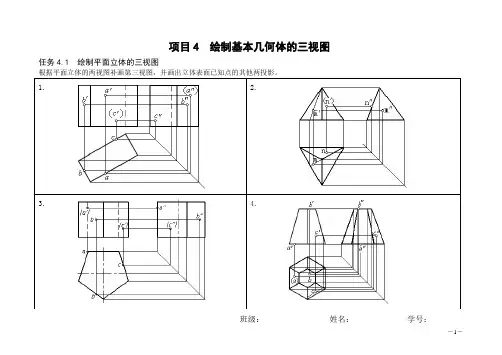
项目4 绘制基本几何体的三视图任务4.1 绘制平面立体的三视图根据平面立体的两视图补画第三视图,并画出立体表面已知点的其他两投影。
1.2.3.4.班级:姓名:学号:任务4.2 绘制回转体的三视图根据回转体的两视图补画第三视图,并画出立体表面已知点的其他两投影。
1.2.3.4.班级:姓名:学号:任务4.3 绘制平面切割体1.补画主、俯视图中的漏线。
2.补画主、左视图中的漏线。
3.补画主、左视图中的漏线。
4.补画俯、左视图中的漏线。
班级:姓名:学号:5.补全截交五棱柱的俯、左视图。
6.补全截交正四棱锥的俯、左视图。
7.补全截交正四棱柱的俯、左视图。
8.补全截交四棱柱的俯视图。
班级:姓名:学号:任务4.4 绘制回转切割体1.补全截交圆柱体的左视图。
2.补全截交圆锥体的主视图。
3.补全截交圆柱体的左视图。
4.补全截交圆柱体的左视图。
班级:姓名:学号:5.补全截交半球体的俯、左视图。
6.补全截交圆柱体的主、俯视图。
7.补画截交同轴回转体的左视图。
8.补全截交同轴回转体的俯视图。
班级:姓名:学号:任务4.5 求作相贯线1.补全相贯圆柱体的主视图。
2.补全相贯圆柱孔的主视图。
3.补全相贯圆柱孔的主视图。
4.补画主视图。
班级:姓名:学号:5.补全相贯圆柱体的主视图。
6.补全相贯圆柱孔的主视图。
7.补全相贯体的主视图。
8.补全相贯体的左视图。
班级:姓名:学号:9.补全相贯体的主视图。
10.补全相贯体的主、俯视图。
11.补全相贯体的主、俯视图。
12.补全相贯体的主视图。
班级:姓名:学号::1. 2.班级:姓名:学号:3. 4.班级:姓名:学号:-11-。

1.1.5 三视图1.能画出简单空间图形的三视图.(重点)2.能识别三视图所表示的立体模型.(重点)3.利用三视图的画法及其特征作组合体的三视图.(难点)4.三视图、直观图、原空间几何体形状之间的相互转化.(难点)教材整理三视图阅读教材P21~P23“例1”以上内容,完成下列问题.1.正投影的定义和性质(1)定义:在物体的平行投影中,如果投射线与投射面垂直,则称这样的平行投影为正投影.(2)性质①垂直于投射面的直线或线段的正投影是点;②垂直于投射面的平面图形的正投影是直线或直线的一部分.2.三视图的分类及画法(1)分类图1164(2)三视图的画法规则①主、俯视图都反映物体的长度——“长对正”;②主、左视图都反映物体的高度——“高平齐”;③俯、左视图都反映物体的宽度——“宽相等”.(3)三视图的排列顺序:先画主视图,左视图在主视图的右边,俯视图在主视图的下边.如果一个几何体的主视图和左视图都是长方形,那么这个几何体不可能是( )A.长方体B.圆柱C.三棱柱D.正三棱锥【解析】长方体和圆柱的主视图和左视图可能是长方形,当三棱柱为直棱柱时,其主视图和左视图可能都是长方形.【答案】 D(1) (2) (3)图1165【精彩点拨】确定正前方→画主视图→画左视图→画俯视图【自主解答】三视图如图①②③所示.1.务必做到长对正,宽相等,高平齐.2.三视图的安排方法是主视图与左视图在同一水平位置,且主视图在左,左视图在右,俯视图在主视图的正下方.3.若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,要注意实、虚线的画法.1.画出如图1166所示几何体的三视图.图1166【解】图为正六棱柱,主视图和左视图都是矩形,主视图中有两条竖线,左视图中有一条竖线,俯视图是正六边形..【导学号:45722021】图1167【精彩点拨】欲画出该几何体的三视图,先弄清它是由什么简单几何体按什么方式构成的,然后确定主视、左视、俯视的方向,最后按三视图的画法规则画出它的三视图.【自主解答】该物体是由一个正六棱柱和一个圆柱组合而成的,主视图反映正六棱柱的三个侧面和圆柱的侧面,左视图反映正六棱柱的两个侧面和圆柱的侧面,俯视图反映该物体投影后是一个正六边形和一个圆(中心重合),故它的三视图如图.画组合体的三视图的“四个步骤”1.析:分析组合体的组成形式.2.分:把组合体分解成简单几何体.3.画:画分解后的简单几何体的三视图.4.拼:将各个三视图拼合成组合体的三视图.2.画出如图1168所示的几何体的三视图.图1168【解】探究1该几何体是什么吗?并试着画出图形.图1169【提示】由三视图可知,该几何体为正四棱锥,如图所示.探究2 如何结合三视图还原几何体?【提示】根据三视图还原几何体,要仔细分析和认真观察三视图并进行充分的想象,然后结合三视图的形状,从不同的角度去还原.看图和想图是两个重要的步骤,“想”于“看”中,形状分析的看图方法是解决此类问题的常用方法.根据三视图(如图1170所示)想象物体原形,指出其结构特征,并画出物体的实物草图.图1170【精彩点拨】由主视图、左视图确定几何体为锥体,再结合俯视图确定其是四棱锥,由俯视图可知其底面形状,再结合主视图、左视图所给信息画直观图.【自主解答】由俯视图知,该几何体的底面是一直角梯形;再由主视图和左视图知,该几何体是一四棱锥,且有一侧棱与底面垂直,所以该几何体如图所示.由三视图还原几何体时,一般先由俯视图确定底面,由主视图与左视图确定几何体的高及位置,同时想象视图中每一部分对应实物部分的形状.3.如图1171是一个物体的三视图,则此三视图所描述的物体是下列哪个几何体?( )图1171【解析】由俯视图可知该几何体为旋转体,由主视图、左视图可知该几何体由圆锥、圆柱组合而成.【答案】 D1.下列哪个几何体的三视图可能全是一样的平面图形( )A.长方体B.圆柱C.正四棱锥D.正方体【答案】 D2.已知某物体的三视图如图1172所示,那么这个物体的形状是( )图1172A.长方体B.圆柱C.正方体D.圆锥【解析】俯视图是圆,所以为旋转体,可排除A、C,又主、左视图为矩形,所以不是圆锥,排除D.故选B.【答案】 B3.水平放置的下列几何体,主视图是长方形的是______(填序号).①②③④图1173【解析】①③④的主视图为长方形,②的主视图为等腰三角形.【答案】①③④4.一物体及其主视图如图1174:①②③④图1174则它的左视图与俯视图分别是图形中的________.【解析】左视图是矩形中间有条实线,应选③;俯视图为矩形中间有两条实线,且为上下方向,应选②.【答案】③②5.如图1175所示的三视图表示的几何体是什么?画出物体的形状.【导学号:45722022】图1175【解】该三视图表示的是一个四棱台,如图.。
姓名,年级:时间:§3三视图1.由基本几何体形成的组合体有两种基本的组成形式:(1)将基本几何体拼接成组合体;(2)从基本几何体中切掉或挖掉部分构成组合体.2.绘制三视图时的注意点(1)主、俯视图长对正;主、左视图高平齐;俯、左视图宽相等,前后对应.(2)在三视图中,需要画出所有的轮廓线,其中,视线所见的轮廓线画实线,看不见的轮廓线画虚线.(3)同一物体放置的位置不同,所画的三视图可能不同.(4)清楚简单组合体是由哪几个基本几何体组成的,并注意它们的组成方式,特别是它们的交线位置.判断正误(正确的打“√”,错误的打“×”)(1)任何几何体的三视图都与其摆放的位置有关.( )(2)任何几何体的三视图都与其摆放的位置无关.()(3)有的几何体的三视图与其摆放的位置无关.()(4)正方体的三视图一定是三个全等的正方形.( )[答案] (1)×(2)×(3)√(4)×题型一简单几何体的三视图【典例1】画出如图所示几何体的三视图.[思路导引]图①为正六棱柱,可按棱柱的画法画出,图②为一个圆锥与一个圆台的组合体,按圆锥、圆台的三视图画出它们的组合形状.[解] 按正六棱柱、圆锥、圆台的三视图画法如图所示.(1)画三视图时,首先确定主视、左视、俯视的方向,同一物体放置的位置不同,所画的三视图可能不同.一般主视方向确定了,则左视与俯视的方向也就确定了,在有的问题里,直接给出主视图,也是确定主视方向的一个方法.(2)一个物体的三视图的排列规则是:俯视图放在主视图的下面,左视图放在主视图的右面.[针对训练1]如下图所示,图(1)是底面边长和侧棱长都是2 cm 的四棱锥,图(2)是上、下底面半径分别为1 cm,2 cm,高为2 cm的圆台,分别画出它们的三视图.[解](1)四棱锥的三视图如下图所示:(2)圆台的三视图如下图所示:题型二简单组合体的三视图【典例2】画出如图所示的几何体的三视图.[思路导引]画三视图之前,先把几何体的结构弄清楚,图为两个圆柱的组合体.[解] 如图所示.画简单组合体的三视图时要注意的问题(1)分清简单组合体是由哪些简单几何体组成的,是组合型还是切挖型.(2)先画主体部分,后画次要部分.(3)几个视图要配合着画.一般是先画主视图再确定左视图和俯视图.(4)组合体的各部分之间要画出分界线.[针对训练2]画出如图所示几何体的三视图.[解] 如图所示(1)(2)题型三由三视图还原成实物图【典例3】如图是一个物体的三视图,则此三视图所描述的物体是下列哪个几何体( )[思路导引](1)通过主视图和左视图确定是柱体、锥体还是台体.若主视图和左视图为矩形,则原几何体为柱体;若主视图和左视图为等腰三角形,则原几何体为锥体;若主视图和左视图为等腰梯形,则原几何体为台体.(2)通过俯视图确定是多面体还是旋转体,若俯视图为多边形,则原几何体为多面体;若俯视图为圆,则原几何体为旋转体.[解析] 由俯视图可知该几何体为旋转体,由主视图、左视图、俯视图可知该几何体是由圆锥、圆柱组合而成.[答案] D由三视图还原成实物图时,一般先由俯视图确定底面,由主视图与左视图确定几何体的高及位置,同时想象视图中每一部分对应实物部分的形状.[针对训练3]根据三视图(如图所示)想象物体原形,指出其结构特征,并画出物体的实物草图.[解]由俯视图知,该几何体的底面是一直角梯形;再由主视图和左视图知,该几何体是一四棱锥,且有一侧棱与底面垂直,所以该几何体如图所示.1.如图,甲、乙、丙是三个立体图形的三视图,与甲、乙、丙相对应的标号是()①长方体;②圆锥;③三棱锥;④圆柱.A.③①② B.①②③ C.③②④ D.④②③[答案] D2.已知三棱柱ABC—A1B1C1如右图所示,以BCC1B1的前面为正前方,画出的三视图正确的是( )[解析]主视图是矩形,左视图是三角形,俯视图是矩形,中间有一条线.[答案] A3.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的主视图的面积不可能等于()A.1 B. 2 C。
组织教学
(1分钟)
规范日常教学管理
复习、导入新课(2分钟)
创设学习情境(5分钟)
激发学生对本课次的学习兴趣,营造良好的学习氛围。
新课讲解
(55分钟)培养学生观察能力和思考能力;培养学生独立思考、合作学习的能力
环视学生:对学生出勤人数,规范着装情况,进行检
查点评。
上节课我们学习了绘制切割圆柱体的三视图,那么,椭圆
是如何绘制的呢?我们回忆一下。
一、四心近似法
已知相互垂直且平分的椭圆长轴和短轴,则椭圆的
近似画法(四心近似法)步骤如下所示:
第一步:
画出长轴AB和短轴CD,连接AC;
第二步:
在AC上截取CF,使其等于AO与CO之差CE;
第三步:
检查
讲授
导入新课
简单讲
解,通过
回忆的方
式,让学
生复习一
下椭圆的
绘制方
法。
做好课
前准备工
作
思考问题
学生观看
课件,思
考教师提
出的问题
作AF的垂直平分线,使其分别交AO和OD(或其延长线)于O1和O2点。
以O为对称中心,找出O1的对称点O3及O2的对称点O4,此O1、O2、O3、O4各点即为所求的四圆心。
通过O2和O1、O2和
O3、O4和O3各点,分别作连线;
第四步:
分别以O2和O4为圆心,O2C(或O4D)为半径画两弧。
再分别以O1和O3为圆心,O1A(或O3B)为半径画两弧,使所画四弧的接点分别位于O2O1、O2O3、O4O1和O4O3的延长线上,即得所求的椭圆
二、讨论问题:
上节课我们学习了绘制切割圆柱体的三视图,那么对于圆锥体,它被切割后会形成一个怎样的图形呢?
圆锥体被切割后所形成的图形如图所示。
让学生在黑板上绘制圆锥体的三视图,让学生们跟着一起绘制圆锥体的三视图,然后再对完整的圆锥体进行切割,通过切割后,引导学生如何绘制成切割圆锥体的三视图,期间应该注意绘制过程中一些需要注意的点,并强调截交线在各个视图上分别是哪些。
其中从切割圆锥体开始要仔细讲解,期间应拿出课前准备的正四棱锥模型,方便于学生理解。
在黑板上
按照国家
标准绘制
正四棱锥
的三视
图,并对
其进行切
割,绘制
切割后的
圆锥体。
让学生拿
出本子和
纸,和老
师一起,
一步一步
来完成圆
锥体的绘
制,并逐
步进行讲
解,让学
生掌握正
四棱锥的
绘制,以
及切割圆
锥体的绘
制方法。
设计思路
时间安排教学内容教师活动学生活动
总结延伸(20)分钟
对知识目标和学生掌握情况进行检测,并通过总结巩固探究,强化认识,提示重,难点知识。
五)回顾本节课的重难点内容,进行总结延伸
一圆锥体是如何被切割的?
圆锥体是被一个正垂面进行切割,其切割后形成的是
一个不规则的图形,我们可以通过先绘制圆锥体完整的视
图,再来进行切割,完成被切割正四棱锥的三视图。
本课次的
知识点总
结归纳延
伸
(注:可编辑下载,若有不当之处,请指正,谢谢!)。