切割体的三视图

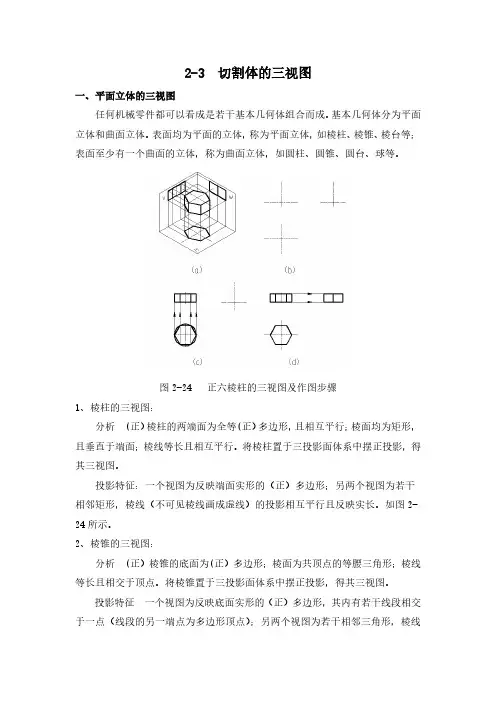
2-3 切割体的三视图一、平面立体的三视图任何机械零件都可以看成是若干基本几何体组合而成。

基本几何体分为平面立体和曲面立体。

表面均为平面的立体，称为平面立体，如棱柱、棱锥、棱台等；表面至少有一个曲面的立体，称为曲面立体，如圆柱、圆锥、圆台、球等。

图2-24 正六棱柱的三视图及作图步骤1、棱柱的三视图：分析 (正）棱柱的两端面为全等(正）多边形，且相互平行；棱面均为矩形，且垂直于端面；棱线等长且相互平行。

将棱柱置于三投影面体系中摆正投影，得其三视图。

投影特征：一个视图为反映端面实形的（正）多边形；另两个视图为若干相邻矩形，棱线（不可见棱线画成虚线）的投影相互平行且反映实长。

如图2-24所示。

2、棱锥的三视图：分析 (正）棱锥的底面为(正）多边形；棱面为共顶点的等腰三角形；棱线等长且相交于顶点。

将棱锥置于三投影面体系中摆正投影，得其三视图。

投影特征一个视图为反映底面实形的（正）多边形，其内有若干线段相交于一点（线段的另一端点为多边形顶点）；另两个视图为若干相邻三角形，棱线（不可见棱线画成虚线）的投影相交于一点。

如图2-25所示。

图2-25 四棱锥的三视图及作图步骤3、棱（锥）台的三视图：分析（正）棱台的两底面为相似(正）多边形，且相互平行；棱面为等腰梯形；棱线等长且延长相交于锥顶。

将棱台置于三投影面体系中摆正投影，得其三视图。

投影特征一个视图为反映底面实形的相似（正）多边形，棱线的收缩投影连接相似多边形对应顶点；另两个视图为若干相邻梯形，棱线（不可见棱线画成虚线）的投影延长交于棱锥台的锥顶。

如图2-26所示。

图2-26 三棱锥和四棱锥的三视图二、平面立体被截切后的三视图用平面截切平面立体，平面与立体表面产生交线，称之为截交线，该平面称为截平面，如图2-27所示。

由于立体的形状各有不同，截平面的位置也有不同，导致截交线的形状也各不相同，但它们都具有以下基本特性：图2-27 截交线实例（1）截交线为封闭的平面图形。

任务一绘制切割体的三视图学习目标巩固三视图相关知识；知道截断体，掌握截交线。

能熟练运用表面取点法求解截交线。

任务分析图1—1 顶尖立体图如图1—1所示的顶尖，基本形状由大圆柱、小圆柱和圆锥三部分叠加，经切割而成，其轮廓线既包括基本体形状图线，也包括截交线。

这样的立体在现实生活中很多，要绘制这类立体的三视图，除了必备前面所学的三视图知识，还得学会截交线求作方法，综合运用才能绘制这类立体的三视图。

知识拓展一、截交线被截断后的基本几何体称为截断体，用来截断几何体的平面称为截平面，截平面与立体表面的交线称为截交线，截交线是封闭的曲线，由截交线围成的平面图形称为截面。

（一）平面体的截交线平面与平面体相交（平面体被截断），所得的交线是由直线组成的封闭多边形，该多边形的边就是平面体表面与截平面的交线，其顶点是棱线与截平面的交点。

求平面体的截交线，关键是找到截平面与立体棱线的共有点（截平面与立体各棱线的交点），然后将各点连接即为所求。

[例1—1] 如图1—2所示为一四棱柱被一正垂面截切，求截交线。

图1—2 四棱柱的截交线分析：四棱柱被截切，上底有两条边被截切，侧面有三条棱被截切，共有5条棱被截切，产生五个交点，截面为五边形。

此题的关键就是求作A、B、C、D、E五个顶点的投影。

先在主视图中标注出这些点，按投影关系在俯视图中找到对应的点，再按投影规律作出这些点的左视图投影，然后连接即为所求。

注意：1．要判别图线的可见性。

2．若立体被两相交平面截断，两截平面相交处有交线（交点在立体表面上），切不可漏画。

如图1—3所示。

图1—3 截切后的三棱柱（二）回转体的截交线1．圆柱的截断圆柱被截切后产生的截交线，因平面与圆柱轴线的相对位置不同而不同，可以分为三种情况，见表1—1所示。

表1—1 平面截切圆柱的截交线截平面位置平行于轴线垂直于轴线倾斜于轴线截交线矩形圆椭圆轴测图投影图[例1—2] 求圆柱被一正垂面截切后的截交线。

如图1—4。