_整式及其运算
- 格式:ppt
- 大小:682.00 KB
- 文档页数:33


整式运算公式汇总整式是由常数、变量及其乘积所构成的代数表达式,常见的整式运算包括加法、减法、乘法和除法。
下面是整式运算的一些常用公式汇总。
1.加法和减法:-任意两个整式之和或之差仍然是整式。
2.乘法:-一个整数与一个整式相乘,所得结果仍然是整式。
-两个整式相乘时,可以利用分配律进行展开。
-两个含有相同的因子的整式相乘时,可以利用公因式提取法进行合并。
3.乘方:a^n表示a的n次方,在整式运算中,可以使用以下公式进行乘方运算:-a^m*a^n=a^(m+n)(底数相同的乘方,指数相加)-(a^m)^n=a^(m*n)(乘方的乘方,指数相乘)-a^0=1(任何数的0次方等于1)4.除法:整式的除法运算可以利用乘法的逆运算,即乘法逆元素,其中,除法过程可以通过因式分解、相除法或多项式长除法等方法进行。
5.因式分解:将一个整式分解为几个不可再分解的乘积形式的过程称为因式分解。
常见的因式分解公式包括:-公因式提取法:将一个整式中的公因子提取出来。
-二次差分公式:a^2-b^2=(a+b)(a-b)- 平方差公式:a^2 + b^2 = (a+b)^2 - 2ab- 三次方差公式:a^3 - b^3 = (a-b)(a^2 + ab + b^2)6.基本恒等式:- 乘法结合律:a(bc) = (ab)c- 乘法交换律:ab = ba-加法结合律:(a+b)+c=a+(b+c)-加法交换律:a+b=b+a- 加法与乘法的分配律:a(b+c) = ab+ac这些是整式运算的一些常见公式,它们在代数运算中起到重要的作用。
通过熟练掌握和运用这些公式,可以更好地理解和解决整式运算问题。

整式的概念与运算整式是代数中的重要概念,广泛应用于数学和科学领域。
本文将介绍整式的概念和运算规则,并且通过实例进行详细说明,以便读者更好地理解整式的特点和运算方法。
一、整式的概念整式是由常数、变量及它们的乘积和积的和构成的代数式。
整式可以包含一个或多个变量,并且可以对变量进行加、减、乘、除等运算。
一般来说,整式是多项式的一种特殊形式。
1.1 单项式当整式中只包含一个变量的乘积时,称为单项式。
例如:2x,-3xy,4a^2b等都是单项式。
其中,x、y、a、b是变量,2、-3、4是系数。
1.2 多项式当整式中包含多个单项式时,称为多项式。
例如:3x^2 - 2xy + 5是一个多项式。
其中,3x^2、-2xy、5都是单项式。
二、整式的运算整式的运算包括加法、减法、乘法和除法。
下面将分别介绍各种运算规则,并通过实例进行说明。
2.1 加法和减法整式的加法和减法运算规则与数的加法和减法类似。
只需将同类项(具有相同的变量和相同的指数)的系数相加或相减即可。
例如:3x^2 + 2xy - 5 和 -2x^2 - 3xy + 4 是两个整式,它们可以进行相加运算:(3x^2 + 2xy - 5) + (-2x^2 - 3xy + 4) = (3x^2 - 2x^2) + (2xy - 3xy) + (-5+ 4) = x^2 - xy - 12.2 乘法整式的乘法运算规则是将每一项的系数相乘,并将变量和指数相乘。
例如:(2x + 3)(4x - 5)是一个整式乘法运算,可以按照分配律展开运算:(2x + 3)(4x - 5) = 2x * 4x + 2x * (-5) + 3 * 4x + 3 * (-5) = 8x^2 - 10x + 12x - 15 = 8x^2 + 2x - 152.3 除法整式的除法运算需要借助长除法的方法进行求解。
例如:将12x^2 + 8x + 4除以4x,可以进行如下的除法运算:3x + 1--------------4x | 12x^2 + 8x + 412x^2 + 4x----------4x + 44x + 1-------3所以,商为3x + 1,余数为3。


整式的运算知识点总结整式是由字母、数字和运算符号组成的多项式,是代数学中常见的基本表达形式。
整式的运算是代数学中较为基础的内容之一,掌握整式的运算方法对于解决代数问题至关重要。
本文将对整式的运算知识点进行总结,包括整式的加减乘除以及相关的运算性质。
一、整式的加法和减法运算整式的加法和减法是最基础的运算,需要注意以下几点:1. 相同项的加减:对于相同的字母和指数的项,可以直接按照系数相加减的原则进行合并。
例如:3x^2 + 4x^2 = 7x^2;5y - 2y = 3y。
2. 不同项的加减:对于不同的项,无法进行合并。
可以将它们按照字母和指数的大小进行排列。
例如:2x^2 + 3x - 5x^2 - 2x = 2x^2 - 5x^2 + 3x - 2x = -3x^2 + x。
二、整式的乘法运算整式的乘法是将两个整式相乘得到一个新的整式,需要注意以下几点:1. 乘法的分配律:对于整式乘以一个数,可以将这个数分别乘以每一项,并将结果相加。
例如:3(2x^2 + 3x) = 6x^2 + 9x。
2. 乘法的合并同类项:乘法运算时,需要合并同类项,即将相同的字母和指数的项合并。
例如:(2x + 3)(4x - 2) = 8x^2 + 4x - 12x - 6 = 8x^2 - 8x - 6。
三、整式的除法运算整式的除法是将一个整式除以另一个整式得到商式和余式的运算,需要注意以下几点:1. 整式的除法并不总是能够完全除尽,有可能存在余数。
2. 设被除式为A(x),除式为B(x),商式为Q(x),余式为R(x),则A(x) = B(x)Q(x) + R(x)。
3. 除法的过程涉及到带余除法的计算步骤,可以利用这个过程来进行整数和多项式的除法。
四、整式的运算性质整式的运算有以下几个基本性质:1. 交换律:加法和乘法都满足交换律,即a + b = b + a,ab = ba。
2. 结合律:加法和乘法都满足结合律,即a + (b + c) = (a + b) + c,a(bc) = (ab)c。
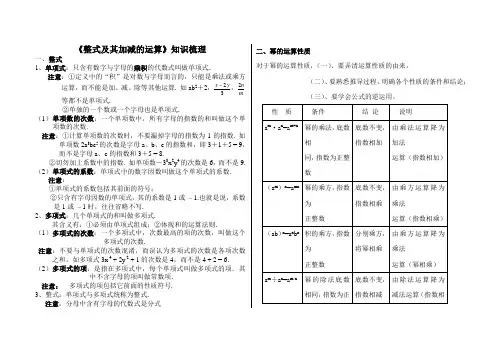
《整式及其加减的运算》知识梳理一、整式1、单项式:只含有数字与字母的乘积的代数式叫做单项式.注意:①定义中的“积”是对数与字母而言的,只能是乘法或乘方运算,而不能是加、减、除等其他运算. 如ab 2+2,32y x ,mn 2等都不是单项式.②单独的一个数或一个字母也是单项式.(1) 单项数的次数:一个单项数中,所有字母的指数的和叫做这个单项数的次数.注意:①计算单项数的次数时,不要漏掉字母的指数为1的指数. 如单项数2a 3bc 5的次数是字母a 、b 、c 的指数和,即3+1+5 = 9,而不是字母a 、c 的指数和3+5 = 8.②切勿加上系数中的指数. 如单项数-33x 2y 4的次数是6,而不是9. (2) 单项式的系数:单项式中的数字因数叫做这个单项式的系数.注意:①单项式的系数包括其前面的符号;②只含有字母因数的单项式,其的系数是1或 – 1.也就是说,系数是1或 – 1时,往往省略不写. 2、多项式:几个单项式的和叫做多项式.其含义有:①必须由单项式组成;②体现和的运算法则.(1)多项式的次数:一个多项式中,次数最高的项的次数,叫做这个多项式的次数.注意:不要与单项式的次数混淆,而误认为多项式的次数是各项次数之和,如多项式3x 4 + 2y 2 + 1的次数是4,而不是4 + 2 = 6. (2)多项式的项:是指在多项式中,每个单项式叫做多项式的项.其中不含字母的项叫做常数项.注意: 多项式的项包括它前面的性质符号. 3、整式:单项式与多项式统称为整式. 注意:分母中含有字母的代数式是分式二、幂的运算性质对于幂的运算性质,(一)、要弄清运算性质的由来,(二)、要熟悉推导过程,明确各个性质的条件和结论;(三)、要学会公式的逆运用。
在学习和运用这些性质时,一要注意符号问题,二要与整式的有关概念及整式的加碱运算相联系,三要注意各个性质的逆向运用及综合运用。
四、熟练的进行整式的三种运算1、整式的加减运算整式的加减包括单项式的加减和多项式的加减,整式加减的基础是去括号和合并同类项,整式加减运算的实质是去括号,合并同类项。



整式的运算知识点整式是指由常数、变量和它们的积或幂次构成的代数表达式。
在代数学中,我们经常需要对整式进行运算,掌握整式的运算知识是解决代数问题的关键。
以下是整式运算的主要知识点:一、加法和减法运算1. 同类项的加法:将系数相同、幂次相同的项相加,例如:3x^2 + 2x^2 = 5x^22. 同类项的减法:将系数相同、幂次相同的项相减,例如:4a^3 - 2a^3 = 2a^33. 非同类项的加减法:对于系数不同或幂次不同的项,无法直接相加减,必须先化简为同类项再进行运算,例如:2x^2 + 3x - 4x^2 + 5 = -2x^2 + 3x + 5二、乘法运算1. 两个整式相乘:将每一项都与另一个整式中的每一项相乘,再将结果相加,例如:(2x + 3)(4x + 5) = 8x^2 + 22x + 152. 多个整式相乘:按照分配律和结合律,逐步进行乘法运算,例如:(a + b)(c + d)(e + f) = ace + acf + ade + adf + bce + bcf + bde + bdf三、指数运算1. 幂的乘法:同一个底数的幂相乘,指数相加,例如:x^2 * x^3 = x^(2+3) = x^52. 幂的除法:同一个底数的幂相除,指数相减,例如:x^4 ÷ x^2 = x^(4-2) = x^23. 幂的乘方:一个幂的指数再次求幂,指数相乘,例如:(x^2)^3 = x^(2*3) = x^6四、分配律1. 乘法与加法的分配律:整式乘以一个因式后再加减,可先分别将整式与因式相乘,再进行加减运算,例如:2x(3x + 4y) = 6x^2 + 8xy2. 乘法与减法的分配律:整式乘以一个因式后再减去,可先分别将整式与因式相乘,再进行减法运算,例如:3a(4b - 2c) = 12ab - 6ac以上是整式的主要运算知识点,掌握了这些知识点,就能够灵活运用整式进行代数计算,并解决各类代数问题。


整式加减乘除公式总结一、整式的基本概念整式是由常数和变量的乘积相加(或相减)而成的代数表达式。
整式的运算包括加法、减法、乘法和除法。
二、整式的加法1. 同类项相加:同类项指的是具有相同的字母和指数的项。
对于同类项的整式,只需将各同类项的系数相加即可,字母和指数保持不变。
2. 不同类项相加:不同类项指的是具有不同字母或不同指数的项。
对于不同类项的整式,直接合并即可,不需要进行合并运算。
三、整式的减法整式的减法运算相当于加上一个相反数。
即,将减数的各项改变符号,然后与被减数进行加法运算。
四、整式的乘法1. 单项式相乘:将两个单项式的系数相乘,字母和指数相乘。
2. 多项式相乘:将一个多项式的每一项与另一个多项式的每一项进行单项式相乘后再相加。
五、整式的除法整式的除法是指将一个整式除以另一个整式,得到一个商式和余式的过程。
1. 除数不为零:当除数不为零时,可以进行整式的除法运算。
2. 除数为零:当除数为零时,整式的除法运算无法进行。
六、整式加减乘除的综合运算整式加减乘除的运算顺序遵循数学运算的基本规则,先乘除后加减。
1. 先进行乘法和除法运算:按照乘法和除法的规则,将整式进行相应的运算。
2. 再进行加法和减法运算:按照加法和减法的规则,将已经经过乘法和除法运算的整式进行相应的运算。
七、整式加减乘除的应用整式的加减乘除在数学中有广泛的应用。
1. 代数方程的解:通过整式的加减乘除运算,可以解决代数方程的求解问题。
2. 几何问题的求解:通过整式的加减乘除运算,可以解决几何问题的求解,如面积、体积等问题。
3. 经济问题的分析:通过整式的加减乘除运算,可以解决经济问题的分析,如成本、收益等问题。
整式加减乘除是数学中常用的运算,它们的应用范围非常广泛。
掌握整式加减乘除的规则和运算方法,能够帮助我们解决各种数学问题,提高数学问题的解决能力。
在学习整式加减乘除的过程中,需要注意运算顺序和规则,避免出现错误。
通过不断练习和应用,我们能够熟练掌握整式加减乘除的技巧,并能灵活运用于实际问题的解决中。
整式及整式的运算一.整式的加减1.单项式:在代数式中,若只含有乘法(包括乘方)运算。
或虽含有除法运算,但除式中不含字母的一类代数式叫单项式.2.单项式的系数与次数:单项式中不为零的数字因数,叫单项式的数字系数,简称单项式的系数;系数不为零时,单项式中所有字母指数的和,叫单项式的次数.3.多项式:几个单项式的和叫多项式.4.多项式的项数与次数:多项式中所含单项式的个数就是多项式的项数,每个单项式叫多项式的项;多项式里,次数最高项的次数叫多项式的次数.5.整式:凡不含有除法运算,或虽含有除法运算但除式中不含字母的代数式叫整式.二.整式分类1.同类项:所含字母相同,并且相同字母的指数也相同的单项式是同类项.2.合并同类项法则:系数相加,字母与字母的指数不变.3.去(添)括号法则:去(添)括号时,若括号前边是“+”号,括号里的各项都不变号;若括号前边是“-”号,括号里的各项都要变号.4.整式的加减:整式的加减,实际上是在去括号的基础上,把多项式的同类项合并.5.多项式的升幂和降幂排列:把一个多项式的各项按某个字母的指数从小到大(或从大到小)排列起来,叫做按这个字母的升幂排列(或降幂排列).注意:多项式计算的最后结果一般应该进行升幂(或降幂)排列. 三.整式的加减概念与定义1、都是数或字母的积的式子叫做单项式,单独的一个数或一个字母也是单项式。
2、单项式中的数字因数叫做这个单项式的系数。
3、一个单项式中,所有字母的指数的和叫做这个单项式的次数。
4、几个单项的和叫做多项式,其中,每个单项式叫做多项式的项,不含字母的项叫做常数项。
5、多项式里次数最高项的次数,叫做这个多项式的次数。
6、把多项式中的同类项合并成一项,叫做合并同类项,合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母部分不变。
7、如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;8、如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
整式的概念和运算整式是代数学中的一个重要概念,它是由字母和常数按照一定的规则组合而成的代数表达式。
整式的运算是代数学中的基础知识之一,它包括了整式的加法、减法、乘法以及整式的因式分解等内容。
下面我们将分别介绍整式的概念以及它的运算规则。
一、整式的概念整式是由字母和常数按照加法、减法的规则组合而成的代数表达式。
字母表示未知数或变量,常数则表示具体的数值。
整式的组成部分可以是单个字母或常数,也可以是字母或常数的组合。
整式的例子包括:3x^2 - 5xy + 2y^2、4a + 7b、-2xyz等。
其中,3x^2 - 5xy + 2y^2是一个二次整式,4a + 7b是一个一次整式,-2xyz是一个三次整式。
整式的次数是指整式中各个项次数的最大值。
例如,3x^2 - 5xy +2y^2的次数为2,4a + 7b的次数为1,-2xyz的次数为3。
二、整式的运算1. 整式的加法和减法整式的加法和减法遵循一般代数表达式的运算规则,即按照同类项相加或相减。
同类项是指具有相同字母部分,并且各个字母的指数也相同的项。
例如,3x^2和2x^2是同类项,因为它们具有相同的字母x和指数2;但是3x^2和2xy^2就不是同类项。
在整式的加法和减法中,我们只需要按照同类项的规则,将各个项的系数相加或相减,同时保持字母和指数不变即可。
例如,对于整式3x^2 - 5xy + 2y^2 和 2x^2 + 3xy - y^2来说,我们可以将它们的同类项相加得到:(3x^2 + 2x^2) + (-5xy + 3xy) + (2y^2 - y^2) = 5x^2 - 2xy + y^2。
2. 整式的乘法整式的乘法是指将两个整式相乘的运算。
在整式的乘法中,需要注意以下几点:(1)对于整式的乘法,一般使用分配律进行计算。
即将一个整式的每一项与另一个整式中的每一项分别相乘,然后将所得的各个乘积相加得到最终结果。
例如,将整式3x^2 - 5xy + 2y^2与2x - y进行乘法运算,我们可以将这两个整式中的每一项分别相乘,并将结果相加:(3x^2)(2x) +(3x^2)(-y) + (-5xy)(2x) + (-5xy)(-y) + (2y^2)(2x) + (2y^2)(-y) = 6x^3 -3x^2y - 10x^2y + 5xy^2 + 4xy^2 - 2y^3 = 6x^3 - 13x^2y + 9xy^2 - 2y^3。