双曲线定义
- 格式:ppt
- 大小:1.69 MB
- 文档页数:18

双曲线的所有定义
双曲线是二次曲线的一种,其定义有多种:
1. 几何定义:双曲线是平面上到两个给定点的距离之差的绝对值等于固定常数的点的轨迹。
这两个给定点称为焦点,常数称为离心率。
2. 解析定义:双曲线的解析方程可以表示为Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0,其中A、B、
C、D、E和F为实数,并且至少一个系数A、B或C不为零。
3. 参数定义:双曲线也可以用参数方程表示,例如x = a sec(t)和y = b tan(t),其中a和b为正
实数,t为参数。
4. 极坐标定义:在极坐标系统中,双曲线的方程可以表示为r^2 = a^2 cos^2(theta) - b^2
sin^2(theta),其中a和b为正实数,theta为极角。
这些定义都描述了双曲线的几何特征和形态。
双曲线具有两个分离的支部,并且在其两个焦点之间有对称轴。
双曲线还具有一些重要的性质,例如渐近线、焦点和定点的关系等。

双曲线第四定义整理如下:一般的,双曲线是定义为平面交截直角圆锥面的两半的一类圆锥曲线。
它还可以定义为与两个固定的点(叫做焦点)的距离差是常数的点的轨迹。
下面是整理的双曲线的定义及标准方程,供参考。
1双曲线的定义(1)平面内,到两个定点的距离之差的绝对值为常数(小于这两个定点间的距离)的点的轨迹称为双曲线。
定点叫双曲线的焦点。
(2)平面内,到给定一点及一直线的距离之比为常数e(e=c/a(e>1),即为双曲线的离心率)的点的轨迹称为双曲线。
定点叫双曲线的焦点,定直线叫双曲线的准线。
双曲线准线的方程为x=±a²/c(焦点在x轴上)或y=±a²/c(焦点在y轴上)。
(3)一平面截一圆锥面,当截面与圆锥面的母线不平行,且与圆锥面的两个圆锥都相交时,交线称为双曲线。
(4)在平面直角坐标系中,二元二次方程F(x,y)=ax2+bxy+cy2+dx+ey+f=0满足以下条件时,其图像为双曲线。
(a、b、c不都是零,b2-4ac>0)2双曲线的标准方程标准方程1:焦点在X轴上时为x2/a2-y2/b2=1(a>0,b>0)标准方程1:焦点在Y轴上时为y2/a2-x2/b2=1(a>0,b>0)双曲线取值范围:│x│≥a(焦点在x轴上)或者│y│≥a(焦点在y轴上)双曲线对称性:关于坐标轴和原点对称,其中关于原点成中心对称。
1、双曲线顶点A(-a,0),A'(a,0)。
同时 AA'叫做双曲线的实轴且│AA'│=2a。
B(0,-b),B'(0,b)。
同时 BB'叫做双曲线的虚轴且│BB'│=2b。
F1(-c,0)或(0,-c),F2(c,0)或(0,c)。
F1为双曲线的左焦点,F2为双曲线的右焦点且│F1F2│=2c对实轴、虚轴、焦点有:a2+b2=c22、双曲线离心率第一定义:e=c/a 且e∈(1,+∞)第二定义:双曲线上的一点P到定点F的距离│PF│与点P到定直线(相应准线)的距离d 的比等于双曲线的离心率e。




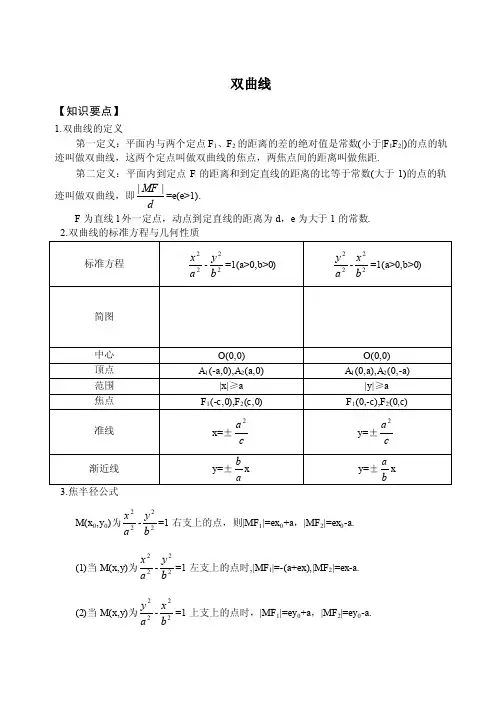
双曲线【知识要点】1.双曲线的定义第一定义:平面内与两个定点F 1、F 2的距离的差的绝对值是常数(小于|F 1F 2|)的点的轨迹叫做双曲线,这两个定点叫做双曲线的焦点,两焦点间的距离叫做焦距.第二定义:平面内到定点F 的距离和到定直线的距离的比等于常数(大于1)的点的轨迹叫做双曲线,即dMF ||=e(e>1). F 为直线l 外一定点,动点到定直线的距离为d ,e 为大于1的常数. 2.双曲线的标准方程与几何性质M(x 0,y 0)为22a x -22b y =1右支上的点,则|MF 1|=ex 0+a ,|MF 2|=ex 0-a.(1)当M(x,y)为22a x -22b y =1左支上的点时,|MF 1|=-(a+ex),|MF 2|=ex-a.(2)当M(x,y)为22a y -22bx =1上支上的点时,|MF 1|=ey 0+a ,|MF 2|=ey 0-a.【基础训练】1.(2004年春季北京)双曲线42x -92y =1的渐近线方程是 ( )A.y =±23xB.y =±32xC.y =±49xD.y =±94x2.过点(2,-2)且与双曲线22x -y 2=1有公共渐近线的双曲线方程是( )A.22y -42x =1B.42x -22y =1C.42y -22x =1D.22x -42y =13.如果双曲线642x -362y =1上一点P 到它的右焦点的距离是8,那么P 到它的右准线距离是( )A.10B.7732 C.27 D.5324.已知圆C 过双曲线92x -162y =1的一个顶点和一个焦点,且圆心在此双曲线上,则圆心到双曲线中心的距离是____________. 5.求与圆A :(x +5)2+y 2=49和圆B :(x -5)2+y 2=1都外切的圆的圆心P 的轨迹方程为________________.【典型例题】题型一:求双曲线的标准方程例1、 根据下列条件,求双曲线的标准方程:(1)与双曲线92x -162y =1有共同的渐近线,且过点(-3,23);(2)与双曲线162x -42y =1有公共焦点,且过点(32,2).(3)实轴长为16,离心率为45e(4)经过两点P )7,26()72,3(---Q题型二:双曲线的定义及应用例2、(2002年全国,19)设点P 到点M (-1,0)、N (1,0)距离之差为2m ,到x 轴、y 轴距离之比为2,求m 的取值范围.例3、如下图,在双曲线122y -132x =1的上支上有三点A (x 1,y 1),B (x 2,6),C (x 3,y 3),它们与点F (0,5)的距离成等差数列. (1)求y 1+y 3的值;(2)证明:线段AC 的垂直平分线经过某一定点,并求此点坐标.变式:、已知(2,1),A F ,P 是曲线221(0)x y x -=>上一点,当||||2PA PF +取最小值时,P 的坐标是,|||PA PF 最小值是 .题型三:双曲线的性质及应用例4、 已知双曲线22a x -22by =1的离心率e >1+2,左、右焦点分别为F 1、F 2,左准线为l ,能否在双曲线的左支上找一点P ,使得|PF 1|是P 到l 的距离d 与|PF 2|的等比中项?变式:过双曲线22a x -22by =1.的右焦点F 作渐近线的垂线,垂足为M ,交双曲线的左右两支于A 、B 两点,求双曲线离心率的取值范围。


双曲线的概念、方程及性质一、知识梳理1. 双曲线定义:平面内到两定点21,F F 的距离之差的绝对值为常数(小于||21F F )的点的轨迹叫双曲线,两定点21,F F 叫双曲线的焦点,||21F F 叫焦距.注:当||||||||2121F F MF MF <-时轨迹是 ;当||||||||2121F F MF MF =-时轨迹是 ;当||||||||2121F F MF MF >-时轨迹是 .2.双曲线的标准方程:焦点在x 轴上: )0,(12222>=-b a b y a x ,焦点在x 轴上:)0,(12222>=-b a bx a y ;统一式)0(122<=+AB By Ax3. 双曲线的几何性质:范围、对称性、顶点、离心率、渐近线、第二定义、焦半径、等轴双曲线及离心率、共轭双曲线、共渐近线的双曲线系二、专题训练1、根据下列条件分别求出双曲线的标准方程(1)以1F (-6,0),2F (6,0)为焦点,且过P (5,2)点;(2)焦点在y 轴上,分别过M (3,-42)和N (9/4,5);(3)离心率为5/3,经过点M (35/2,2);(4)以043=±y x 为渐近线,一条准线为0335=+y .2.双曲线11622=-m y x 的离心率为45,则m= 3.设P 为11222=-y x 上的一点,1F 、2F 是其两个焦点,若 ||1PF :|P 2F |2:3=,求21F PF S ∆ 4.过双曲线2213y x -=的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A ,B 两点,则AB =5.已知双曲线()222210,0x y a b a b -=>> 的一条渐近线过点( ,且双曲线的一个焦点在抛物线2y = 的准线上,则双曲线的方程为( )(A )2212128x y -= (B )2212821x y -=(C )22134x y -=(D )22143x y -= 6、若双曲线C:22221x y a b-=(0a >,0b >)的一条渐近线被圆()2224x y -+=所截得的弦长为2,则C 的离心率为( )A .2BC D7、已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ,.若经过F 和(0,4)P 两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )(A )22144x y -= (B )22188x y -=(C )22148x y -=(D )22184x y -=8、已知双曲线C 22221x y a b-=(a >0,b >0)的右顶点为A ,以A 为圆心,b 为半径作圆A ,圆A 与双曲线C 的一条渐近线交于M 、N 两点.若∠MAN =60°,则C 的离心率为________.例1、在ABC ∆中, A (-4,0),B (4,0),若1sin sin sin 2A B C -=,求顶点C 的轨迹方程.9、求到定点F (0,-5)与到定直线5/9:-=y l 的距离之比为5/3的点的轨迹.10、动圆M 与圆A :1)3(22=++y x 和圆B :9)3(22=+-y x 均外切,求圆心M 的轨迹方程.11、已知双曲线C :14491622=-y x 的左右焦点分别为1F 、2F ,点P 在曲线C 上.(1) 写出其焦点坐标、准线方程、渐近线方程、离心率;(2) 写出其共轭双曲线的方程;(3) 若32||||21=PF PF ,求21PF F ∠的大小.。

高考数学双曲线的定义知识点复习
高考数学双曲线的定义知识点一
1.双曲线定义的文字表述
双曲线,是指一动点移动于一个平面上,与平面上两个定点的距离的差的绝对值始终为一定值时所成的轨迹叫做双曲线。
2.双曲线定义的分析
1点:两个定点,一个动点
2距离:三个
3量:两个常数
4关系式:两个;一个等式,一个不等式
3.判断一个动点轨迹是否是双曲线的标准
1看动点到两个定点的距离的差的绝对值是否为常数
2看这个常数是否小于两个定点之间的距离
高考数学双曲线的定义知识点二
感谢您的阅读,祝您生活愉快。
