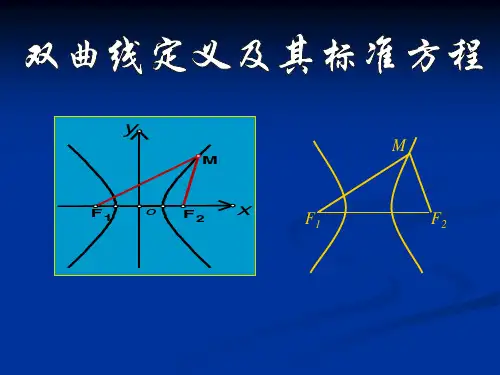
双曲线定义(带动画)

双曲线的定义和性质
双曲线（Hyperbolic Curve）是数学中一种特殊的曲线，它具有两条反曲线（Hyperbolic curve），沿着直线封闭，它被认为是一种极限曲线，可以收敛到两个不同
的焦点。

虽然双曲线也称为平行双曲线，但它们可以按照任意方向曲折，但不会超过可以
认为是一个自治空间内的某个最大距离。

双曲线常用来描述流动的几何形状，可以用来解
释力的重力学传播效应。

（1）双曲线的最重要的性质就是它收敛到两个焦点，且这两个焦点之间的距离可以
通过一个称为双曲线的焦距的值来衡量。

（2）另外，双曲线完全由两个反曲线（Hyperbolic curves）组成，沿着直线封闭，
且双曲线具有节点，这些节点与直线联系在一起，称为切点，切点与双曲线的凹角相关联。

（3）此外，双曲线还具有两个定点，它们位于曲线上，且称为双曲线的交点，即双
曲线截止点。

双曲线的曲率（Curvature）取决于双曲线的焦距，曲率越大，双曲线的弯
曲越明显。

（4）双曲线的面积是负的，这意味着它的形状并不完全似圆，而是更加具有弯曲性，因此它在空间中形状更复杂。

（5）双曲线具有相反性，也就是说，当它在一个方向运行时，它会在相反的方向运行。

（6）另外，双曲线的拉伸性也很高，可以曲折的的角度和弯曲程度要比普通圆弧更大，这也使它具有很多实用价值。

（7）双曲线可以用于许多不同的几何计算，如极限几何的计算，倒立曲线的计算以
及复杂的曲面的几何计算。

双曲线的定义1．双曲线的定义【定义】双曲线（Hyperbola）是指与平面上到两个定点的距离之差的绝对值为定值的点的轨迹，也可以定义为到定点与定直线的距离之比是一个大于 1 的常数的点之轨迹．双曲线是圆锥曲线的一种，即圆锥面与平面的交截线．双曲线在一定的仿射变换下，也可以看成反比例函数．两个定点F1，F2 叫做双曲线的焦点（focus），定直线是双曲线的准线，常数e 是双曲线的离心率．【标准方程】푥2푎2①―푦2푏2=1（a，b＞0），表示焦点在x 轴上的双曲线；푦2푎2②―푥2푏2=1（a，b＞0），表示焦点在y 轴上的双曲线．【性质】푥2푎2这里的性质以―푦2푏2=1（a，b＞0）为例讲解：푎2①焦点为（±c，0），其中c2＝a2+b2；②准线方程为：x＝±；③离心率e =푐푐푏푎＞1；④渐近线：y＝±푎x；⑤焦半径公式：左焦半径：r＝|ex+a|，右焦半径：r＝|ex﹣a|．【实例解析】푥2例 1：双曲线4―푦216= 1 的渐近线方程为푥2解：由4―푦216푥2= 0 可得y＝±2x，即双曲线4―푦216= 1 的渐近线方程是y＝±2x．故答案为：y＝±2x．这个小题主要考察了对渐近线的理解，如果实在记不住，可以把那个等号后面的 1 看成是 0，然后因式分解得到的两个式子就是它的渐近线．例 2：已知双曲线的一条渐近线方程是x﹣2y＝0，且过点P（4，3），求双曲线的标准方程解：根据题意，双曲线的一条渐近线方程为x﹣2y＝0，1/ 2푥2设双曲线方程为4―y2＝λ（λ≠0），∵双曲线过点P（4，3），424∴― 32＝λ，即λ＝﹣5．푥2∴所求双曲线方程为4―y2＝﹣5，푦2即：5―푥220= 1．一般来说，这是解答题的第一问，常常是根据一些性质求出函数的表达式来，关键是找到a、b、c 三者中的两者，最后还要判断它的焦点在x 轴还是y 轴，知道这些参数后用待定系数法就可以直接写出函数的表达式了．【考点点评】这里面的两个例题是最基本的，必须要掌握，由于双曲线一般是在倒数第二个解答题出现，难度一般也是相当大的，在这里可以有所取舍，对于基础一般的同学来说，尽量的把这些基础的分拿到才是最重要的，对于还剩下的部分，尽量多写．2/ 2。

双曲线的定义及其基本性质
一、双曲线的定义：
（1）到两个定点F 1与F 2的距离之差的绝对值等于定长（＜
2
1F F ）的点的轨迹。

两定点叫双曲线的焦点。

a PF PF 221=-＜2
1F F
（2）动点P 到定点F 的距离与到一条定直线的距离之比是常数e （e ＞1）时，这个动点的轨迹是双曲线。

这定点叫做双曲线的焦点，定直线l 叫做双曲线的准线。

二、双曲线的方程： 双曲线标准方程的两种形式：
①
12
222=-b y a x ，2
2b a c +=，
F 1(-c,0),F 2(c,0) 三、双曲线的性质：
（1）焦距F 1F 2=2c,实轴长A 1A 2=2a,虚轴长（2）双曲线的离心率为e=a
c
，e>1（3）焦点到渐近线的距离：虚半轴长b （4）有两条准线，c a x l 21:-=x l 2:=四、双曲线的渐近线：
（1）若双曲线为12222=-b y a x ⇒渐近线方程为x a
b
y ±=，
（2）若已知某双曲线与12222=-b y a x 有公共渐近线，则可设此双曲线为λ=-22
22b
y a x ，
（3）特别地当a=b 时⇔2=e ⇔两渐近线互相垂直，分别为y =±x ，此时双曲线为等轴双曲线
五、共轭双曲线：
双曲线A 的实轴为双曲线B 的虚轴，双曲线A 的虚轴为双曲线B 的实轴，即11
122=+B
A e e 。