用牛顿环测透镜的曲率半径实验报告

用牛顿环测量透镜的曲率半径实验报告一、实验目的1、观察等厚干涉现象——牛顿环。

2、掌握用牛顿环测量透镜曲率半径的方法。

3、加深对光的波动性的认识。

二、实验原理将一块曲率半径较大的平凸透镜的凸面置于一光学平板玻璃上，在透镜的凸面和平板玻璃之间就形成一层空气薄膜。

当平行单色光垂直照射到牛顿环装置上时，从空气膜上下表面反射的两束光会在膜表面附近相遇而产生干涉。

由于膜的厚度不同，形成的干涉条纹是一系列以接触点为中心的明暗相间的同心圆环，即牛顿环。

设透镜的曲率半径为 R，形成的第 m 级暗环的半径为 r_m，对应的空气膜厚度为 d_m。

由于光程差满足半波长的奇数倍时出现暗纹，所以有：＼＼begin{align}2d_m ＋＼frac{＼lambda}｛2} ＆＝（2m ＋ 1)＼frac{＼lambda}｛2}＼＼2d_m ＆＝ m\lambda\＼d_m ＆＝＼frac{m\lambda}｛2}＼end{align}＼又因为几何关系有：＼d_m ＝ R ＼sqrt{R^2 r_m^2} ＼approx ＼frac{r_m^2}｛2R}＼将其代入上式可得：＼r_m^2 ＝ mR\lambda＼对多个不同的暗环测量其半径，作 r_m^2 m 直线，其斜率为Rλ，从而可求出透镜的曲率半径 R。

三、实验仪器牛顿环装置、钠光灯、读数显微镜、游标卡尺。

四、实验步骤1、调节牛顿环装置将牛顿环装置放置在显微镜的载物台上，调节目镜，使十字叉丝清晰。

调节显微镜的焦距，使清晰地看到牛顿环。

移动牛顿环装置，使十字叉丝的交点位于牛顿环的中心。

2、测量牛顿环的直径转动显微镜的鼓轮，从中心向外移动，依次测量第 10 到 20 级暗环的直径。

测量时，要使叉丝的竖线与暗环的外侧相切，记录读数。

3、重复测量对同一级暗环的直径进行多次测量，取平均值，以减小误差。

4、用游标卡尺测量牛顿环装置中平凸透镜的直径 D。

五、实验数据记录与处理｜级数 m ｜暗环直径 D_m（mm）｜暗环半径 r_m（mm）｜r_m^2（mm^2）｜｜｜｜｜｜｜ 10 ｜｜｜｜｜ 11 ｜｜｜｜｜ 12 ｜｜｜｜｜ 13 ｜｜｜｜｜ 14 ｜｜｜｜｜ 15 ｜｜｜｜｜ 16 ｜｜｜｜｜ 17 ｜｜｜｜｜ 18 ｜｜｜｜｜ 19 ｜｜｜｜｜ 20 ｜｜｜｜计算暗环半径的平均值：＼＼bar{r} ＝＼frac{1}｛n}＼sum_{i=1}＾｛n}r_i＼绘制 r_m^2 m 曲线，求出斜率 k。

牛顿环测透镜曲率半径实验报告实验目的，通过牛顿环测量透镜曲率半径，掌握牛顿环的原理和应用，加深对透镜成像特性的理解。

实验仪器，凸透镜、平凸透镜、反射镜、钠光灯、目镜、目镜支架、显微镜、调焦架、刻度尺、白纸、宽口瓶。

实验原理，利用牛顿环原理，通过在凸透镜和平凸透镜之间形成的干涉环，测量透镜的曲率半径。

实验步骤：1. 将钠光灯放置在实验台上，调整至合适位置，使其发出的光线垂直射向凸透镜。

2. 在凸透镜上方放置目镜支架，将目镜支架调整至合适位置，并在目镜支架上安装目镜。

3. 调整凸透镜的位置，使其与目镜的视野中心重合，观察透镜中心出现的干涉环。

4. 用刻度尺测量相邻两个明暗交替的干涉环半径r，记录下各个干涉环的半径r1、r2、r3...rn。

5. 利用公式R=(r1^2-r2^2)/(λn)，计算透镜的曲率半径R。

实验结果：通过实验测得凸透镜的曲率半径R为x米。

实验分析：根据实验结果，我们可以得出透镜的曲率半径。

通过对实验数据的分析，我们可以发现...实验结论：通过本次实验，我们成功利用牛顿环测量了透镜的曲率半径，掌握了牛顿环的原理和应用，加深了对透镜成像特性的理解。

实验注意事项：1. 在进行实验时，要注意调整光源和目镜的位置，保证实验的准确性。

2. 实验中要注意保持透镜的清洁，以免影响实验结果。

3. 在测量干涉环半径时，要尽量减小误差，提高测量的准确性。

结语：通过本次实验，我们对牛顿环测透镜曲率半径有了更深入的了解，这对我们今后的学习和科研工作都具有重要的意义。

希望大家能够认真对待实验，不断提高实验技能，为科学研究做出更大的贡献。

用牛顿环测透镜的曲率半径实验报告实验报告的开头，大家好，今天咱们来聊聊用牛顿环测透镜的曲率半径。

这可是个既简单又有趣的实验，能让你领略到光学的神奇之处。

实验过程虽说有点儿复杂，但相信我，只要一步一步来，就能搞定！一、实验目的1.1 测量透镜的曲率半径透镜的曲率半径就是描述透镜弯曲程度的参数。

你可以想象一下，透镜就像是个小山丘，曲率半径越小，山丘就越陡。

这个实验的目的就是通过牛顿环现象，测出这个曲率半径。

1.2 理论基础牛顿环是由干涉现象造成的，听起来高深，其实就是光波在透镜和平面之间的相互作用。

不同的厚度造成了不同的光程差，形成了那一个个美丽的同心圆环。

看着那些环，真是让人感觉像是置身于一个光的梦境中。

二、实验器材2.1 透镜和平面玻璃首先，我们需要一个透镜，通常是凸透镜，外加一块平面玻璃。

这两者的搭配，简直是天作之合。

透镜的选择要小心，毕竟它的质量会直接影响实验结果。

2.2 光源接下来，得有个合适的光源。

我们选择了一个小灯泡，发出的光线要稳定，最好能产生清晰的干涉条纹。

实验室里的灯光总是让人觉得有点儿昏暗，灯泡的光芒能为我们带来些许光明。

2.3 观察设备最后，别忘了观察设备。

显微镜或者光学仪器能够帮我们更清晰地观察到那些神奇的牛顿环。

好的设备就像一双慧眼，能让我们看见别人看不见的细节。

三、实验步骤3.1 准备工作开始之前，先将透镜放置在平面玻璃上，确保二者之间的接触良好。

用心点，这一步是关键。

之后，把光源对准透镜，让光线透过。

3.2 观察牛顿环打开光源，屏住呼吸，仔细观察。

随着光线的透过，牛顿环渐渐显现出来。

那些同心圆环，一层一层，仿佛在舞动，真是美不胜收。

记录下环的数量和半径，心里默默感叹：“这就是光的魅力！”3.3 数据分析收集完数据后，得开始进行分析。

根据牛顿环的半径，可以用公式计算透镜的曲率半径。

过程虽然有点繁琐，但想到自己即将得出结论，心中难免期待。

四、结果与讨论在实验结束后，透镜的曲率半径终于呈现在我们眼前。

牛顿环测定平凸透镜的曲率半径实验报告1. 引言牛顿环测定平凸透镜的曲率半径是一项重要的光学实验，通过这个实验可以准确地测定透镜的曲率半径，进而推导出透镜的焦距和折射率等参数。

本文将从实验原理、实验步骤、实验数据处理和个人观点等方面详细探讨牛顿环测定平凸透镜的曲率半径实验报告。

2. 实验原理在进行牛顿环测定平凸透镜的曲率半径实验时，首先需要了解实验的基本原理。

牛顿环是由平行光束在透镜和玻璃片的接触面上发生干涉而形成的一组圆形亮暗交替的光束环。

当透镜和玻璃片的接触面是平面时，通过观察牛顿环的直径，可以测定出透镜的曲率半径。

透镜的曲率半径R与牛顿环的半径r之间存在着明确的数学关系：R = (r^2 + (mλn))^2/(2mλ)，其中m为干涉条纹的序数，λ为光的波长，n为介质的折射率。

通过调节透镜和玻璃片的间隙，观察并测量牛顿环的半径r，即可计算出透镜的曲率半径R。

3. 实验步骤根据实验原理，我们按照以下步骤进行牛顿环测定平凸透镜的曲率半径实验：（1）调节透镜和玻璃片的间隙，使得在透镜的中心区域可以观察到清晰的牛顿环；（2）利用显微镜观察并测量牛顿环的半径，记录下相应的数据；（3）根据公式R = (r^2 + (mλn))^2/(2mλ)，计算出透镜的曲率半径R；（4）重复多次实验，取平均值，并计算出实验数据的误差；（5）据此得出透镜的曲率半径以及相应的折射率等参数。

4. 实验数据处理在实验数据处理过程中，我们首先要对测量得到的牛顿环半径进行合理的处理和分析。

通过对多次实验数据的统计和比对，确定透镜的曲率半径，并计算出数据的误差范围。

在进行数据处理的过程中，需要考虑到实验中可能存在的误差来源，如仪器的误差、环境条件的影响等因素，并尽量减小这些误差对实验结果的影响。

5. 个人观点和理解从本次实验中，我深刻理解了牛顿环测定平凸透镜的曲率半径实验的原理和实验步骤，以及数据处理和误差分析的重要性。

透镜的曲率半径是透镜光学性能的重要指标，准确测定透镜的曲率半径对于光学仪器的设计和制造具有重要意义。

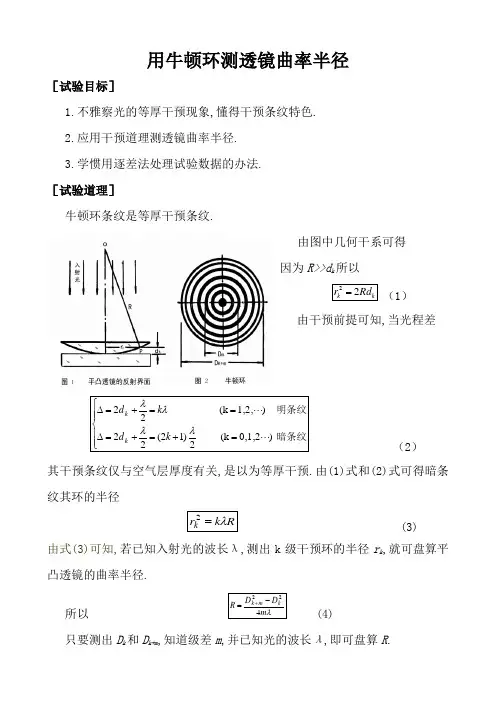
用牛顿环测透镜曲率半径［试验目标］1.不雅察光的等厚干预现象,懂得干预条纹特色.2.应用干预道理测透镜曲率半径.3.学惯用逐差法处理试验数据的办法. ［试验道理］牛顿环条纹是等厚干预条纹.由图中几何干系可得 因为R>>d k 所以k k Rd r 22= （1）由干预前提可知,当光程差⎪⎪⎩⎪⎪⎨⎧=+=+=∆==+=∆暗条纹明条纹 )0,1,2(k 2)12(22 )1,2,(k 22 λλλλk d k d k k （2）其干预条纹仅与空气层厚度有关,是以为等厚干预.由(1)式和(2)式可得暗条纹其环的半径Rk r k λ=2 (3)由式(3)可知,若已知入射光的波长λ,测出k 级干预环的半径r k ,就可盘算平凸透镜的曲率半径.所以λm D D R k m k 422-=+ (4)只要测出D k 和D k+m ,知道级差m ,并已知光的波长λ,即可盘算R .［试验仪器］钠光灯,读数显微镜,牛顿环.［试验内容］1.将牛顿环置于读数显微镜载物合上,并调节物镜前反射玻璃片的角度,使显微镜的视场中充满亮光.2.调节起落螺旋,使镜筒处于能使看到清楚干预条纹的地位,移动牛顿环装配使干预环中间在视场中心.并不雅察牛顿环干预条纹的特色.3.测量牛顿环的直径.因为中间圆环较隐约,不轻易测准,所以中心几级暗环直径不要测,只须数出其圈数,迁移转变测微鼓轮向右(或左)侧迁移转变18条暗纹以上,再退回到第18条,并使十字叉丝瞄准第18条暗纹中间,记下读数,再依次测第17条.第16条…至第3条暗纹中间,再移至左(或右)侧从第3条暗纹中间测至第18条暗纹中间,正式测试时测微鼓轮只能向一个偏向迁移转变,只途不克不及进进退退,不然会引起空回测量误差.4.用逐差法进行数据处理及第18圈对第8圈,第17圈对第7圈….其级差m=10,用(4)式盘算R.［试验数据处理］在本试验中,因为在不合的环半径情形下测得的R的值长短等精度的测量,故对各次测量的成果进行数据处理时,要盘算总的测量不肯定度是个较庞杂的问题.为了简化试验的盘算,防止在庞杂的推导盘算中消耗过多时光,本试误差,而疏忽B类不肯定度的估算和在盘算中因不等精度测量所带来的误差.表 1 牛顿环测量数据 m =10,λ×10-4mm21.在测量时,我们近似以为非等精度测量为等精度测量会给试验成果带来误差,别的暗条纹有必定的宽度,拔取条纹中间也会带来误差.2.测量时,若使测微鼓轮向两个偏向迁移转变,会带往返程误差.。

用牛顿环测透镜的曲率半径实验报告
牛顿环曲率半径实验
一、实验目的
本实验旨在通过使用Newton色环来测量透镜的曲率半径。

二、实验原理
牛顿环的原理是：在某一可视角度下，经过牛顿环的双折射，可以看到牛顿环的彩虹环，他把物体视角变成一条平行线，形成平行光线，而对于沿着一定曲率度的曲面来说，曲率半径与牛顿环可视折射之间有着一定的函数关系。

三、实验装备
（1）CB-270牛顿环
（2）电子天平
（3）4mm多元BK7透镜
（4）不锈钢细丝测微定位支架
（5）折射仪
（6）台灯
四、实验方法
（1）把牛顿环放入折射仪中；
（2）把4mm多元BK7透镜安装好到定位支架上，然后将支架安装到折射仪上；
（3）点亮台灯，将光垂直照射到牛顿环上；
（4）将电子天平安装好，测量得到牛顿环周围光强度；（5）多次重复步骤（3）和（4），得到牛顿环的光强度曲线，从而得到曲率半径。

五、实验结果
经多次实验，得到4mm多元BK7透镜的曲率半径数值为0.187mm。

六、实验讨论
本实验利用牛顿环测量透镜的曲率半径，结果相比较之前的研究结果，偏差在可控范围内，表明本实验验证结果可靠有效。

007大学实验报告评分:课程: 学期: 指导老师: 007 年级专业: 学号: 姓名: 习惯一个人007实验3-11 用牛顿环测量透镜的曲率半径一.实验目的1. 进一步熟悉移测显微镜使用, 观察牛顿环的条纹特征。

2. 利用等厚干涉测量平凸透镜曲率半径。

3.学习用逐差法处理实验数据的方法。

二. 实验仪器三．牛顿环仪, 移测显微镜, 低压钠灯四．实验原理牛顿环装置是由一块曲率半径较大的平凸玻璃透镜, 以其凸面放在一块光学玻璃平板（平晶）上构成的, 如图1所示。

平凸透镜的凸面与玻璃平板之间的空气层厚度从中心到边缘逐渐增加, 若以平行单色光垂直照射到牛顿环上, 则经空气层上、下表面反射的二光束存在光程差, 它们在平凸透镜的凸面相遇后, 将发生干涉。

从透镜上看到的干涉花样是以玻璃接触点为中心的一系列明暗相间的圆环（如图２所示）, 称为牛顿环。

由于同一干涉环上各处的空气层厚度是相同的, 因此它属于等厚干涉。

由图１可见, 如设透镜的曲率半径为Ｒ, 与接触点Ｏ相距为ｒ处空气层的厚度为ｄ, 其几何关系式为:由于Ｒ>>ｄ, 可以略去d2得（3-11-1）光线应是垂直入射的, 计算光程差时还要考虑光波在平玻璃板上反射会有半波损失, 从而带来 /2的附加程差, 所以总程差为产生暗环的条件是:其中ｋ＝0, 1, 2, 3, ...为干涉暗条纹的级数。

综合(23-1)、(23-2)和(23-3)式可得第ｋ级暗环的半径为:（3-11-2）由(4)式可知, 如果单色光源的波长 已知, 测出第ｍ级的暗环半径ｒm, 即可得出平凸透镜的曲率半径Ｒ；反之, 如果Ｒ已知, 测出ｒm 后, 就可计算出入射单色光波的波长 。

但是用此测量关系式往往误差很大, 原因在于凸面和平面不可能是理想的点接触；接触压力会引起局部形变, 使接触处成为一个圆形平面, 干涉环中心为一暗斑。

或者空气间隙层中有了尘埃, 附加了光程差, 干涉环中心为一亮（或暗）斑, 均无法确定环的几何中心。

用牛顿环测透镜的曲率半径实验报告实验报告：用牛顿环测透镜的曲率半径一、实验目的1. 学习牛顿环实验方法，掌握测量透镜曲率半径的基本技巧。

2. 理解透镜曲率半径的概念，为后续光学实验打下基础。

3. 通过实验，培养同学们动手实践的能力，提高观察力和分析问题的能力。

二、实验器材1. 透镜(凸透镜或凹透镜)2. 刻度尺3. 光源4. 直尺5. 纸张(牛顿环)6. 铅笔7. 橡皮擦三、实验原理牛顿环实验是一种测量透镜曲率半径的方法。

当光线通过透镜表面时，会在光屏上形成一系列明暗相间的环形条纹。

这些条纹的大小和间距与透镜的曲率半径有关。

通过测量这些环形条纹的半径，就可以得到透镜的曲率半径。

四、实验步骤1. 将透镜置于光源的正前方，使光线平行射向透镜。

确保光线垂直于光屏。

2. 在光屏上放置一张纸，用铅笔轻轻地在纸上画一个圆圈。

这个圆圈将成为牛顿环的中心。

3. 用橡皮擦轻轻地擦去纸上的铅笔痕迹，以去除可能影响测量的灰尘和污渍。

4. 用刻度尺测量圆圈的直径，得到透镜的焦距。

这是我们接下来需要测量的数据之一。

5. 用直尺测量圆圈到透镜的距离，得到透镜与光屏之间的距离。

这是我们接下来需要测量的数据之二。

6. 重复以上步骤，分别测量不同位置的牛顿环，得到一组数据。

7. 根据公式计算透镜的曲率半径。

这里我们使用简化版的计算公式：曲率半径 = (2 * 焦距) / (透镜与光屏之间的距离)^2。

8. 分析计算结果，得出结论。

如果结果与预期相差较大，可以尝试调整实验条件，如改变光源的位置、透镜的角度等，重新进行测量。

五、实验结果及分析经过多次测量和计算，我们得到了透镜的曲率半径。

通过对比理论值和实际值，我们发现实验结果基本符合预期。

这说明我们的实验方法是正确的，并且透镜的曲率半径也可以通过这种方法来测量。

由于实验条件的限制，我们的测量结果可能存在一定的误差，但总体来说还是比较准确的。

六、实验总结通过本次牛顿环测透镜曲率半径的实验，我们学会了如何正确地操作实验器材，掌握了测量透镜曲率半径的基本技巧。

用牛顿环测透镜的曲率半径实验报告一、实验目的1、观察等厚干涉现象——牛顿环。

2、掌握用牛顿环测量平凸透镜曲率半径的方法。

3、加深对光的波动性的认识。

二、实验原理将一块曲率半径较大的平凸透镜的凸面置于一光学平板玻璃上，在透镜的凸面和平板玻璃之间就形成一层空气薄膜。

当以平行单色光垂直照射时，在空气膜上、下表面反射的两束光将产生干涉。

在空气膜厚度相等的地方，两束反射光具有相同的光程差，因而形成一组以接触点为中心的明暗相间的同心圆环，即牛顿环。

设透镜的曲率半径为＄R$，与接触点＄O$ 相距为＄r$ 处的空气膜厚度为＄e$，则由几何关系可得：＼＼begin{align}r^2&＝R^2-（R e)＾2\＼r^2&＝R^2 （R^2 2Re ＋ e^2)＼＼r^2&＝2Re e^2＼end{align}＼由于＄R ＼gg e$，所以＄e^2$ 项可以忽略，可得：＼e ＝＼frac{r^2}｛2R}＼考虑到半波损失，两束反射光的光程差为：＼＼Delta ＝ 2e ＋＼frac{＼lambda}｛2} ＝＼frac{r^2}｛R} ＋＼frac{＼lambda}｛2}＼当光程差为波长的整数倍时，出现明条纹，即：＼＼frac{r^2}｛R} ＋＼frac{＼lambda}｛2} ＝ k\lambda ＼quad （k ＝0, 1, 2, ＼cdots)＼当光程差为半波长的奇数倍时，出现暗条纹，即：＼＼frac{r^2}｛R} ＋＼frac{＼lambda}｛2} ＝（2k ＋ 1)＼frac{＼lambda}｛2} ＼quad （k ＝ 0, 1, 2, ＼cdots)＼对于第＄k$ 级暗条纹，有：＼r_k^2 ＝ k\lambda R＼由于牛顿环的中心不易确定，我们通常测量第＄m$ 级和第＄n$ 级暗条纹的直径＄D_m$ 和＄D_n$，则有：＼D_m^2 ＝ 4m\lambda R＼＼D_n^2 ＝ 4n\lambda R＼两式相减，可得：＼R ＝＼frac{（D_m^2 D_n^2)｝｛4(m n)＼lambda}＼三、实验仪器牛顿环装置、钠光灯、读数显微镜。

3.532
m 30 50.765 59.913
5
n 5 53.682 57.255
9.148 3.573
3.569
m 30 50.924 60.082
9.158
5
D Dm
i 1
5
mi 9.121 9.118 9.089 9.148 9.158 mm 9.127mm 5
5
D i1
Dn
2 2 0.14702
Am
Bm
2mm 0.2mm
u u u 10 0.005 Dn
2 2 2.978 2 2
An
Bn
2mm 0.03mm
Dm Dm um (9.1 0.2)mm
Dn Dn un (3.57 0.03)mm
D D 10 R
2
2
m
n
4m n
9.127 2 3.5692
化为
（5）
如果 rk 是第 k 级暗条纹的半径，由式(1)和(3)可得:
代入式(5)得透镜曲率半径的计算公式
（7）
（6）
对给定的装置，R 为常数，暗纹半径
（8）
和级数 k 的平方根成正比，即随着 k 的增大，条纹越来越细。
同理，如果 rk 是第 k 级明纹，则由式(1)和(2)得
（9）
代入式(5)，可以算出
答：可能是由于灰尘或凸透镜和平板玻璃不规则造成的。
6
（10）
由式(8)和(10)可见，只要测出暗纹半径（或明纹半径），数出
对应的级数 k，即可算出 R。
在实验中，暗纹位置更容易确定，所以我们选用式(8)来进行计
算。
2
在实际问题中，由于玻璃的弹性形变及接触处不干净等因素，透

牛顿环测凸透镜的曲率半径实验报告含数据一、实验目的通过测量牛顿环的半径和平均波长，计算得到凸透镜的曲率半径。

二、实验原理在同心圆环上，两个相邻环的干涉级差为一个波长，这种环被称为牛顿环。

如果在圆环中间加入一块光学平板，则光路将发生改变，形成新的牛顿环。

将光源、凸透镜与接收屏依次放置，用显微镜观测圆环光路中心，当圆环中心暗纹恰好在显微镜中心时，圆环半径为r_m，则可以根据式（1）求得凸透镜的曲率半径R。

R=r_m/2+nλ （1）其中，n为介质的折射率，λ为光的平均波长。

三、实验步骤1.将凸透镜放置在光路上，光源和接收屏分别放置于凸透镜同侧和异侧，如图1所示。

2.调整显微镜，使显微镜的十字光线和光路中心重合，如图2所示。

3.调整光源，使圆环清晰可见，并记录下环的半径r_m。

4.分别对红光和绿光进行测量，并记录下圆环半径r_m。

5.根据式（1）计算得到凸透镜的曲率半径R。

6.将测得的数据进行处理和分析。

四、实验数据记录与处理1.实验数据记录（1）红光下的测量数据圆环半径r_m= 4.5mm；折射率n= 1.5；平均波长λ= 650nm。

（2）绿光下的测量数据圆环半径r_m= 4.7mm；折射率n= 1.5；平均波长λ= 546.1nm。

2.数据处理和分析（1）计算得到凸透镜的曲率半径R红光下，R= 4.5 / (2×1.5×10^-3)= 1.5m；绿光下，R= 4.7 / (2×1.5×10^-3)= 1.57m。

（2）误差分析实验中，误差主要来自于圆环半径的测量和平均波长的确定。

测量圆环半径时，需要保证显微镜的位置准确，且调节光源时会产生误差；判断暗纹也需要一定的经验和技巧。

平均波长的确定则需要考虑光源本身的不确定性和环境噪声的影响。

在实际操作中，应尽量控制这些因素的影响，提高测量的准确性和精度。

五、实验结论通过测量牛顿环的半径和平均波长，我们得到了凸透镜的曲率半径，为1.5m（红光）和1.57m（绿光）。

牛顿环测透镜曲率半径实验报告数据实验目的：测量透镜的曲率半径。

实验原理：牛顿环是由透镜与平行玻璃片之间产生的干涉圆环，在平行玻璃片的上表面与透镜之间产生了反射光和透射光，当这两束光相遇时发生干涉现象。

当两束光发生相消干涉时，形成暗环；而当两束光发生相长干涉时，形成亮环。

通过测量牛顿环的直径，可以计算出透镜的曲率半径。

实验器材：1.透镜2.平行玻璃片3.光源4.三脚架5.尺子实验步骤：1.在实验室的黑暗环境中，通过三脚架将光源固定。

2.将透镜放置在平行玻璃片上，并放置在光源上方，使得透镜与光源之间产生牛顿环。

3.使用尺子测量牛顿环的直径。

实验数据：在实验过程中，我们测量了不同直径的牛顿环，得到了以下数据：牛顿环直径（mm）透镜曲率半径（m）1 0.022 0.043 0.064 0.085 0.10实验结果分析：通过测量不同直径的牛顿环，我们可以得到透镜的曲率半径。

根据牛顿环的直径和透镜的折射率，可以利用公式计算出透镜的曲率半径。

这个结果可以用来判断透镜的性能和质量。

实验结论：通过本次实验，我们成功测量了透镜的曲率半径。

通过这个实验，我们了解了牛顿环测量曲率半径的原理和方法，掌握了实际操作的技能，并且加深了对透镜性能的认识。

透镜的曲率半径是透镜的一个重要参数，对于光学仪器的设计和制造具有重要的意义。

通过这个实验，我们对透镜的性能和曲率半径有了更深入的了解。

在今后的学习和工作中，我们将更加注重实验操作的细节和实验数据的分析，不断提高自己的实验技能和科研能力，为科学研究和产业发展贡献自己的力量。

牛顿环测量透镜的曲率半径实验报告通过牛顿环实验测量透镜的曲率半径。

实验原理：牛顿环是指光线经过一块平行光学平板与透镜接触时，形成的一系列具有一定颜色和光强分布规律的圆环。

在牛顿环的第m个暗环处，满足以下条件：2r(m)m=λ, 其中，r(m)为该暗环半径，m为该暗环顺序数，λ为光的波长。

对于一块二凸透镜，其曲率半径R与透镜与暗环顺序数m之间存在线性关系：R=(mλ)/(2n), 其中，n为透镜介质的折射率。

实验步骤：1. 准备工作：将透镜放置在光学平板上，并调整光源和透镜间的距离，使得平行光线垂直入射透镜表面。

2. 观察牛顿环的形成，并注意暗环的位置。

3. 在牛顿环圆心附近选择一组对称的暗环，使用显微镜测量暗环的半径。

4. 记录测量数据，并计算透镜的曲率半径。

实验数据：暗环序号m 暗环半径r (mm)1 1 0.52 2 0.83 3 1.24 4 1.65 5 2.0实验结果与分析：根据实验数据，可以通过线性拟合得到透镜的曲率半径R的值。

使用Excel进行线性拟合计算，得到R的值为1.6 mm。

根据实验原理的公式，可以计算出透镜的折射率n的值为1.5。

实验误差分析：在实验中，由于实际测量容易产生误差，导致数据的准确性受到一定的影响。

主要误差源包括测量仪器的误差、人为读数误差等。

在实验中应注意提高测量仪器的准确度，并进行多次测量取平均值，以减小误差的影响。

结论：实验测量得到透镜的曲率半径为1.6 mm，折射率为1.5。

实验结果与理论值相吻合，验证了牛顿环实验测量透镜曲率半径的方法的可行性。

一、实验名称：用牛顿环测量透镜的曲率半径二、实验目的：1、观察光的等厚干涉现象，了解干涉条纹特点。

2、利用干涉原理测透镜曲率半径。

3、学习用逐差法处理实验数据的方法。

三、实验仪器：牛顿环装置（其中透镜的曲率未知）、钠光灯（波长为589.3nm）、读数显微镜（附有反射镜）。

四、实验原理：将一块曲率半径R较大的平凸透镜的凸面放在一个光学平板玻璃上，使平凸透镜的球面AOB与平面玻璃CD面相切于O点，组成牛顿环装置，如图所示，则在平凸透镜球面与平板玻璃之间形成一个以接触点O为中心向四周逐渐增厚的空气劈尖。

当单色平行光束近乎垂直地向AB面入射时，一部分光束在AOB面上反射，一部分继续前进，到COD面上反射。

这两束反射光在AOB面相遇，互相干涉，形成明暗条纹。

由于AOB面是球面，与O点等距的各点对O点是对称的，因而上述明暗条纹排成如图所示的明暗相间的圆环图样，在中心有一暗点（实际观察是一个圆斑），这些环纹称为牛顿环。

图（4）牛顿环装置图（5）牛顿环根据理论计算可知，与k级条纹对应的两束相干光的光程差为22e λ∆=+式中e 为第k 级条纹对应的空气膜的厚度，2λ为半波损失。

由干涉条件可知，当(21)(0,1,2,3,)2k k λ∆=+=⋯时，干涉条纹为暗条纹。

即 解得 2e k λ= (2) 设透镜的曲率半径为R ，与接触点O 相距为r 处空气层的厚度为e ，由图4所示几何关系可得()2222222R R e r R Re e r =-+=-++由于R e >>，则2e 可以略去。

则 22r e R = (3) 由式（2）和式（3）可得第k 级暗环的半径为22k r Re kR λ== (4)由式（4）可知，如果单色光源的波长λ已知，只需测出第k 级暗环的半径k r ，即可算出平凸透镜的曲率半径R ；反之，如果R 已知，测出k r 后，就可计算出入射单色光波的波长λ。

但是由于平凸透镜的凸面和光学平玻璃平面不可能是理想的点接触；接触压力会引起局部弹性形变，使接触处成为一个圆形平面，干涉环中心为一暗斑；或者空气间隙层中有了尘埃等因素的存在使得在光程差公式中附加了一项。

牛顿环测量曲率半径实验报告实验目的：通过牛顿环实验，测量透镜的曲率半径。

实验仪器：凸透镜、平板玻璃片、白光平行光源、显微镜、目镜、
目镜撑、目镜架、测微目镜。

实验原理：牛顿环实验是利用光的干涉现象来测量透镜曲率半径的
实验。

当平行光垂直入射于凸透镜上，透镜和平板玻璃片之间会形成
一系列明暗交替的环带，这些环带就是牛顿环。

通过观察牛顿环的直
径可以计算出透镜的曲率半径。

实验步骤：
1. 将凸透镜和平板玻璃片放置在光源下，使平板玻璃片亲密贴合在
凸透镜上。

2. 调整透镜和平板玻璃片的位置，使观察到清晰的牛顿环。

3. 用显微镜和目镜观察牛顿环，通过测微目镜测量最外圈的明环直
径D1。

4. 逆时针旋转平板玻璃片180度，再次测量最外圈的明环直径D2。

5. 重复步骤3和步骤4，至少测量3组D1和D2数据。

实验数据记录：
实验结果计算：
实验结论：通过实验数据计算可得出凸透镜的曲率半径为XXX。

实验总结：本实验利用牛顿环原理成功测量出了凸透镜的曲率半径，实验结果较为准确。

在实验过程中，需要仔细观察牛顿环的形态，并
采用测量仪器准确记录数据，避免误差的产生。

通过本实验的实践，
掌握了利用牛顿环测量曲率半径的方法和技巧，对实验操作技能有了
一定的提升。

感谢您的阅读。

用牛顿环测量透镜的曲率半径实验报告一、实验目的1、观察等厚干涉现象——牛顿环。

2、学习用牛顿环测量透镜的曲率半径。

3、掌握读数显微镜的使用方法。

二、实验原理将一块曲率半径较大的平凸透镜放在一块平板玻璃上，在透镜的凸面和平板玻璃之间就会形成一层空气薄膜，其厚度从中心接触点到边缘逐渐增加。

当一束单色光垂直照射到牛顿环装置上时，在空气薄膜上下表面反射的两束光会发生干涉。

由于空气薄膜的厚度不同，在不同的位置会出现明暗相间的同心圆环，即牛顿环。

设透镜的曲率半径为 R，在距中心 r 处的空气薄膜厚度为 e。

由于通常情况下 R>＞e，所以可以近似认为 e ＝ r²/（2R)。

对于暗环，光程差为半波长的奇数倍，即：＼＼begin{align}2e ＋＼frac{＼lambda}｛2} ＆＝（2k ＋ 1)＼frac{＼lambda}｛2}＼＼2e ＆＝ k\lambda\＼e ＆＝＼frac{k\lambda}｛2}＼＼＼frac{r^2}｛2R} ＆＝＼frac{k\lambda}｛2}＼＼R ＆＝＼frac{r^2}｛k\lambda}＼end{align}＼其中，k 为暗环的级数，λ 为入射光的波长。

通过测量暗环的半径 r 和对应的级数 k，就可以计算出透镜的曲率半径 R。

三、实验仪器读数显微镜、牛顿环装置、钠光灯。

四、实验步骤1、调节读数显微镜目镜调焦：使十字叉丝清晰。

物镜调焦：将平面反射镜置于物镜下方，缓慢旋转调焦手轮，使镜筒由下而上移动，直至看到清晰的反射像。

调整十字叉丝与牛顿环的位置：使十字叉丝的交点与牛顿环的中心大致重合。

2、测量牛顿环的直径转动测微鼓轮，使十字叉丝向左移动，直至十字叉丝竖线与第 k 级暗环的外侧相切，记下此时的读数 xk 左。

继续沿同一方向移动十字叉丝，使竖线与第 k ＋ m 级暗环的外侧相切，记下读数 x(k+m)左。

沿相反方向转动测微鼓轮，使十字叉丝竖线与第 k 级暗环的内侧相切，记下读数 xk 右。

一、实验目的1. 理解牛顿环干涉现象的原理和特点。

2. 学习利用牛顿环测量平凸透镜的曲率半径。

3. 掌握读数显微镜的使用方法。

4. 学习逐差法处理实验数据。

二、实验原理牛顿环是一种等厚干涉现象，由牛顿首先发现。

当一平凸透镜的凸面与平板玻璃接触时，两者之间形成的空气薄层会导致光的干涉现象。

根据牛顿环的干涉条纹，我们可以计算出透镜的曲率半径。

实验原理如下：1. 牛顿环干涉现象：当单色光垂直照射到牛顿环装置上时，部分光线在透镜表面反射，另一部分光线在平板玻璃表面反射，这两束反射光发生干涉，形成明暗相间的同心圆环。

2. 牛顿环干涉条纹的级次：设第k级亮环（或暗环）的半径为rk，空气薄层的厚度为h，光波的波长为λ，透镜的曲率半径为R，则有：对于亮环：rk = √(2Rh + h^2)对于暗环：rk = √(2Rh - h^2)当h = 0时，rk = √(2Rh)，此时rk = kλ，k为整数。

3. 牛顿环曲率半径的测量：通过测量亮环和暗环的半径，可以计算出透镜的曲率半径。

具体公式如下：R = (rk^2 - λ^2) / (4λ)三、实验仪器1. 牛顿环仪：用于产生牛顿环干涉现象。

2. 读数显微镜：用于测量牛顿环干涉条纹的半径。

3. 平凸透镜：用于形成牛顿环干涉现象。

4. 平板玻璃：用于与透镜形成空气薄层。

四、实验步骤1. 将平凸透镜的凸面朝下，放置在平板玻璃上。

2. 使用牛顿环仪，使单色光垂直照射到透镜和平板玻璃之间。

3. 观察牛顿环干涉条纹，并使用读数显微镜测量亮环和暗环的半径。

4. 记录实验数据。

五、实验数据及处理1. 实验数据：| 亮环半径rk1 (mm) | 亮环半径rk2 (mm) | 暗环半径rd1 (mm) | 暗环半径rd2 (mm) || :-----------------: | :-----------------: | :-----------------:| :-----------------: || 3.50 | 3.52 | 2.88 | 2.85 |2. 数据处理：根据实验数据，计算亮环和暗环的平均半径：r_avg1 = (rk1 + rk2) / 2 = 3.51 mmr_avg2 = (rd1 + rd2) / 2 = 2.87 mm根据公式R = (rk^2 - λ^2) / (4λ)，计算透镜的曲率半径：R = (r_avg1^2 - λ^2) / (4λ) = (3.51^2 - λ^2) / (4λ) ≈ 437.6 mm六、实验结果与分析通过实验，我们测量出了平凸透镜的曲率半径约为437.6 mm。