当前位置：文档之家 › 组合数学(西安电子科技大学(第二版))第二章母函数_版24样版演示课件.ppt

组合数学(西安电子科技大学(第二版))第二章母函数_版24样版演示课件.ppt

  • 格式：ppt
  • 大小：1.13 MB
  • 文档页数：59

下载文档原格式

  / 59

合集下载

组合数学(第二版)递推关系

组合数学(第二版)递推关系

递推关系
其次,证明an 是通解.若给定一组初始条件
可以仿照齐次方程通解的证明方法,证得相应于条件式 (3.2.11)的解一定可以表示为式 (3.2.10)的形式.
关于 的求法已经解决,这里的主要问题是求式(3.2.2) 的特解an * .遗憾的是寻求特 解还没有一般通用的方法.然而, 当非齐次线性递推关系的自由项f(n)比较简单时,采用 下面的 待定系数法比较方便.
递推关系 【例 3.4.2】 棋盘染色问题:给一个具有1行n 列的1×n
棋盘(见图3.4.1)的每一个 方块涂以红、蓝二色之一,要求相 邻的两块不能都染成红色,设不同的染法共有an 种,试 求an.
图 3.4.1 1×n 棋盘
递推关系
递推关系
【例3.4.3】 交替子集问题:有限整数集合Sn={1,2,…,n} 的一个子集称为交替的, 如果按上升次序列出其元素时,排列 方式为奇、偶、奇、偶、…….例如{1,4,7,8}和 {3,4,11}都是, 而{2,3,4,5}则不是.令gn表示交替子集的数目(其中包括空集), 证明
且有gn=Fn+2.
递推关系
证 显然,g1=2,对应S1 的交替子集为⌀和{1}.g2=3,对应S2 的交替子集为⌀、 {1}、{1,2}.
将Sn 的所有子集分为两部分: (1)Sn-1={1,2,…,n-1}的所有子集; (2)Sn-1的每一个子集加入元素n 后所得子集. 例如,n=4,S4={1,2,3,4}的所有子集划分为两类,即 (1)⌀、{1}、{2}、{3}、{1,2}、{1,3}、{2,3}、{1,2,3}; (2){4}、{1,4}、{2,4}、{3,4}、{1,2,4}、{1,3,4}、 {2,3,4}、{1,2,3,4}.

组合数学课件--第二章第五节 指数型母函数

组合数学课件--第二章第五节 指数型母函数

4
2.11：指数型母函数
为了便于计算，利用上述特点，形式地引进函数。
x1 x1 x x 2 x2 G e ( x) (1 )(1 ) 1! 2! 3! 1! 2! 展开后三次方项
3! 3! 3! x1 x2 x1 x2 x ( ) 1!2! 2!1! 3! 1!2! 2!1! 3! x x 2 x3 x x2 G e ( x) (1 )(1 ) 1! 2! 3! 1! 2! 1 1 1 3 3! 3! 3! x 3 ( )x ( ) 1!2! 2!1! 3! 1!2! 2!1! 3! 3!
e
4x
x x2 x3 1 4 42 43 ... 1! 2! 3!
排列数是4n。
11
2.11：指数型母函数
例4 求1,3,5,7,9这5个数字组成的n位数个数， 要求其中3出现的次数为偶数，其它数字出现的次 数无限制。（用指数型母函数求解）
解：设满足条件的r位数的数目为ar,则序 列a0,a1,a2,…的母函数为：
C (m, k )(e x ) m k (1) k
k 0
m
(m k ) h k C (m, k )[ x ]( 1) h! k 0 h 0
m h
20
2.11：指 )( m k ) ] h! h 0 k 0
k h

m
h
an (1) k C (m, k )( m k ) n
k 0
m
21
n个球放进m个盒子放法总结:
n个球放进m个盒子里，球是否有区别，盒 子是否有区别，是否允许空盒，共有八种情况：
1、有区别,有区别，有空盒
x x Ge ( x) (1 x ...) m 2! 3!

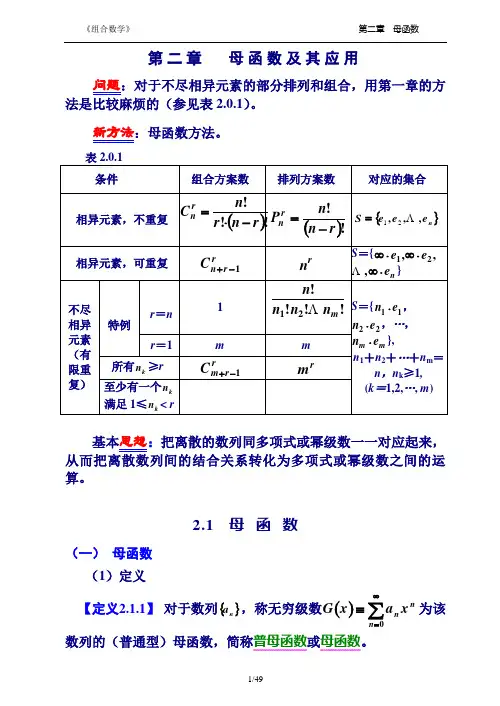
组合数学讲义 2章 母函数

组合数学讲义 2章 母函数

第二章 母函数及其应用问题：对于不尽相异元素的部分排列和组合，用第一章的方2.0.1）。

新方法：母函数方法。

基本思想：把离散的数列同多项式或幂级数一一对应起来，算。

2.1 母 函 数（一） 母函数 （1）定义【定义2.1.1】 对于数列{}n a ，称无穷级数()∑∞=≡0n n n x a x G 为该数列的（普通型）母函数，简称普母函数或母函数。

（2）例【例2.1.1】 有限数列rn C （r ＝0,1,2, …,n ）的普母函数是。

()x G ＝nn n n n nx C x C x C C ++++ 2210＝()nx +1【例2.1.2】 无限数列{1，1，…，1，…}的普母函数是()x G ＝ +++++n x x x 21＝x-11（3）说明● n a 可以为有限个或无限个；● 数列{}n a 与母函数一一对应，即给定数列便得知它的母函数；反之，求得母函数则数列也随之而定；例如，无限数列{0，1，1，…，1，…}的普母函数是+++++nx x x 20＝xx-1● 这里将母函数只看作一个形式函数，目的是利用其有关运算性质完成计数问题，故不考虑“收敛问题”，而且始终认为它是可“逐项微分”和“逐项积分”的。

（4）常用母函数（二） 组合问题 （1）组合的母函数定理2.1.1 组合的母函数：设{}m m e n e n e n S ⋅⋅⋅=,,,2211 ,且n 1＋n 2＋…＋n m ＝n ，则S 的r 可重组合的母函数为()x G ＝∏∑==⎪⎪⎭⎫ ⎝⎛mi n j j i x 10＝∑=n r rr x a 0(2.1.1) 其中，r 可重组合数为rx 之系数r a ，r ＝0,1,2, …,n .理论依据：多项式的任何一项与组合结果一一对应（见例2.1.3）定理2.1.1的优点：● 将无重组合与重复组合统一起来处理； ● 使处理可重组合的枚举问题变得非常简单。

（2）特例推论1 {}n e e e S ,,,21 =，则r 无重组合的母函数为G (x )＝ (1＋x )n (2.1.2)组合数为r x 之系数r n C 。

组合数学课件 第二章母函数与递推关系

组合数学课件 第二章母函数与递推关系
(1 2 x) H ( x) h(1) x [h(2) 2h(1)] x
2 3
[h(3) 2h(2)] x
§2.2
递推关系
根据(2-2-1)，
h(1) 1, h(2) 2h(1) 1, h(3) 2h(2) 1, 2 3 (1 2 x) H ( x) x x x x /(1 x)
§2.2
递推关系
Hanoi问题是个典型的问题，第一步要设 计算法，进而估计它的复杂性，集估计工作量。 算法： N=2时 第二步把下面的一个圆盘移到 C上 第一步先把最上面的一个圆盘套在 B上 最后把 B上的圆盘移到C上 到此转移完毕
A
B
C
§2.2
递推关系
假定n-1个盘子的转移算法已经确定。 对于一般n个圆盘的问题， 先把上面的n-1个圆盘经过C转移到B。 第二步把A下面一个圆盘移到C上 最后再把B上的n-1个圆盘经过A转移到C上
§2.2
递推关系
解法1： 令
an n 位十进制数中出现5的数的个数，
bn n
位十进制数中出现奇数个5的数
的个数。 故有：
an 9an1 bn1 { bn 9bn1 an1 a1 8, b1 1
(2 2 2)
§2.2
递推关系
(2-2-2)式中的 an 9an 1 bn 1表达了 含有偶数个5的n位十进制数的两个组成部分。 9an 1 表达由含有偶数个5的n-1位十进制数 pn 取5以外的0，1，2，3，4， p1 p2 pn1 ，令 6，7，8，9九个数中的一个数构成的。 bn 1 项 表示当 p1 p2 pn1 是含有奇数个5的n-1位十 进制数，令 pn 5 而得 p1 p2 pn是含偶数个 5的n位十进制数。 bn 9bn1 an1也有类似解释。

组合数学(西安电子科技大学(第二版))习题3

组合数学(西安电子科技大学(第二版))习题3

习题三（递推关系）1．解下列递推关系：（1）120171000,1n n n a a a a a ---+=⎧⎨==⎩ （2）12016900,1n n n a a a a a --++=⎧⎨==⎩ （3）20100,2n n a a a a -+=⎧⎨==⎩ （4）120121n n n a a a a a --=-⎧⎨==⎩ （5）123012990,1,2n n n n a a a a a a a ---=+-⎧⎨===⎩ 解：（1）对应的特征方程为：27100x x -+=，解得122,5x x ==。

所以齐次递推方程的通解为：25n n n a A B =+，代入初始条件，得：00a A B =+=，1251a A B =+=，解得：11,33A B =-=， 故 112533n n n a =-+。

（2）对应的特征方程为：2690x x ++=，解得：123x x ==-，所以，齐次递推方程的通解为：()(3)n n a A Bn =+-，代入初始条件，00a A ==，1()(3)1a A B =+-=，解得：10,3A B ==-，故1(3)3n n a n =--。

（3）对应的特征方程为：210x +=，解得：12,x i x i ==-，所以，齐次递推方程的通解为：()()n n n a A i B i =+-，代入初始条件，00a A B =+=，12a A i B i =-=，解得：,A i B i =-=，故 11()()n n n a i i --=+-。

（4）对应的特征方程为：2210x x -+=，解得：121x x ==，所以，齐次递推方程的通解为：n a A Bn =+，代入初始条件，01a A ==，11a A B =+=，解得：1,0A B ==，故 1n a =。

（5）对应的特征方程为：32990x x x --+=，解得：1231,3,3x x x ===-，所以，齐次递推方程的通解为：3(3)n n n a A B C =++-，代入初始条件，00a A B C =++=，1331a A B C =+-=，2992a A B C =++=， 解得，111,,4312A B C =-==-，故 1113(3)412n n n a -=-+--2．求由A ，B ，C ，D 组成的允许重复的排列中AB 至少出现一次的排列数。

1.2.2组合(2)优秀课件2020-2021学年高中数学人教A版选修2-2

1.2.2组合(2)优秀课件2020-2021学年高中数学人教A版选修2-2

C.C83C72 C73C82
D.C83C72C111
4、从7人中选出3人分别担任学习委员、宣传委员、体育委员，
则甲、乙两人不都入选的不同选法种数共有（ ）D
A.C52 A33
B.2C53 A33
C.A53
D.2C52 A33 A53
课堂练习：
5、在如图7x4的方格纸上（每小方格均为正方形） （1）其中有多少个矩形？ （2）其中有多少个正方形？
例5、8双互不相同的鞋子混装在一只口袋中，从中任 意取出4只，试求满足如下条件各有多少种情况：
（1）4只鞋子恰有两双；
（2） 4只鞋子没有成双的；
（3） 4只鞋子只有一双。
课堂练习：
1、把6个学生分到一个工厂的三个车间实习，每个车间2人， 若甲必须分到一车间，乙和丙不能分到二车间，则不同的分
法有 9 种 。
复习巩固：
1、组合定义:
一般地，从n个不同元素中取出m（m≤n）个元素并成一 组，叫做从n个不同元素中取出m个元素的一个组合．
2、组合数:
从n个不同元素中取出m（m≤n）个元素的所有组合的个数 ，叫做从n个不同元素中取出m个元素的组合数，用符号
Cnm 表示.
3、组合数公式:
Cnm
Anm Amm
n(n 1)(n 2) m!
(4)抽出的3件中至多有一件是次品的抽法有多少种？
说明：“至少”“至多”的问题，通常用分类 法或间接法求解。
练习.在产品检验中，常从产品中抽出一部分进行检查. 现有100件产品，其中3件次品，97件正品.要抽出5件 进行检查，根据下列各种要求，各有多少种不同的抽 法？
(1)无任何限制条件； (2)全是正品；
(3)只有2件正品；

《组合数学》课件第2章

《组合数学》课件第2章

1 jn
1i j n
命题 3（加法的结合律） 如果1≤m≤n， 则
aj aj aj aj aj
1 jn
1 jm m jn
1 jm
m jn
第二章 基本计数原理
命题 4（乘法交换律）
ai aj aj ai
1 jm 1 jn
1 jn 1im
命题 5（乘法对加法的分配律）
推论
a aj aaj
1 jn
j0
第二章 基本计数原理
3. 双下标
(a11 a12 a1n ) (a21 a22 a2n ) (am1 am2 amn )
a1 j a2 j amj ( aij )
1 jn
1 jn
1 jn
1im 1 jn
4. 给定数42的所有因子之和
1+2+3+6+7+14+21+42= k
注: 本例指围棋，现代围棋采用十九路，即有19×19=361 个交叉点可落黑子、 白子或留空。
第二章 基本计数原理
例 5 求含有数字1的4位数的个数。 解 先求不含有1的4位数的个数，即求由{0, 2, 3, 4, 5, 6, 7, 8, 9}9个数字组成的4位数的个数（第一位不得出现0）。由乘法原 理，
2a1 b1,2a2 b2 ,,2an bn ,2an1 bn1
第二章 基本计数原理
例 3 某次会议有n位代表参加，已知每一位代表至少认识 其余n-1位中的一位，则n位代表中至少有两位认识的人数相等。
证明 n位代表认识的人数有1, 2, …, n-1， 由鸽巢原理知至少 两位代表认识的人数相等。
第二章 基本计数原理
· 对（2.1.10 №1 定义数组A(1∶N, 1∶N)； №2 对i=1, N, 输入A(i, i)；

组合与二项式23页PPT

组合与二项式23页PPT

m n
m
nmn(n1)(nm 2)L! (nm1)
m
C
m n
n-m n!!m!，Cnn Cn0 1
组合数的性质：
C C 性质1：
m
nm
n
n
C C C 性质2：
m m m1
n1
n
n
解决排列组合问题的方法有：
优限法： 有特殊位置、元素 捆绑法： 相邻 插入法 ： 不相邻 先取后排： 有组合又有排列
N=m1+m2+…+mn 种不同的方法。
分步计数原理
完成一件事，需要分成n个步骤 ，做第一步有m1种不同的方法，做 第二步有m2种不同的方法，……， 做第n步有mn种不同的方法，那么 完成这件事有
N=m1×m2×…×mn 种不同的方法。
排列定义：
从 n 个不同元素中，任取 m (m≤n) 个元素，按照一定的顺序 排成一列，叫做从 n 个不同元素 中取出 m 个元素的一个排列。
例4. 1-90C110+902C210-903C310+… +(-1)k90kCk10+…+9010C1010 除以88的余数是( B )
(A)-1 (B)1 (C)-87 (D)87
9，（ 05江苏）设 k1,2,3,4,5，
则( x 2 ) 5 的展开式中 x k 的系
数不可能是
（C ）
目的要求： 1、分类计数原理与分步计数原理。 2、排列、排列数。 3、组合、组合数、组合数的性质。 4、解决排列组合问题的方法有那 些？
分类计数原理
完成一件事，有n类办法,在第一 类办法中有m1种不同的方法,在第二 类办法中有m2种不同的方法，…… ，在第n类办法中有mn种不同的方法 。那么完成这件事共有

组合数学第二章1母函数PPT课件

组合数学第二章1母函数PPT课件
3
若 有 两 个 色 子 ， 则
( t t 2 . . . t 6 ) ( t t 2 . . . t 6 ) t 2 2 t 3 3 t 4 4 t 5 5 t 6 . . . .
中 的 t 6 的 系 数 5 显 然 相 当 于 t 1 t 5 t 6 , t 2 t 4 t 6 , t 3 t 3 t 6 , t 5 t 1 t 6 , t 4 t 2 t 6 诸 乘 积 都 产 生 t 6 这 一 项 的 方 案 数
[a 0 a 1 x a 2 x 2 ]/1 ( x ) A (x )/1 ( x )
26
2.2 母函数的性质
例. 已知
A (x ) 1 x x 2 x n 1 1 x
B (x ) 1 2 x 3 x2 4 x3 (1 1 x )2
(k1)xk
k0
(11x)2
27
2.2 母函数的性质
证
1:b0 a0a1a2 A(1)
x:b1 a1a2 A(1)a0
x2:b2
a2 A(1)a0a1
_ ) _ _ _ _ _
B (x ) A (1 )1 [x x 2 ] a 0 x (1 x x 2 ) a 1 x 2 (1 x x 2 )
30
2.2 母函数的性质
B(x)1A(1x)(a0a1x )x/1(x)
我们来看如下的例子ppt课件方法的引入我们也可以从另一角度来看要使两个色子掷出6点第一个色子除了6以外的都可选这有5种选法一旦第一个选定第二个色子就只有一种可能的选法按乘法法则有515种注意到出现15有两种选法出现24也有两种选法而出现33只有一种选法这些选法互斥且穷尽了出现6点的一切可能的选法按加法法则共有2215种不同选法
[C(n,0)C(n,1)x C(n,n)xn]

组合数学(西安电子科技大学(第二版))第二章母函数_版24样版

组合数学(西安电子科技大学(第二版))第二章母函数_版24样版

g ( x) (1 x x ....)( 1 x x ...)
3 6 4 8
(1 x 2 x 4 ....)( 1 x 5 x10 ...) 1 1 1 1 3 2 4 5 1 x 1 x 1 x 1 x
sfsf
15
2.1母函数
n
r C n , r x n 0
例 从n双互不相同的五指袜子中取出r只，要求没有任何两只是 成对的，共有多少种不同的取法？
r r C n , r 2 x 解：生成函数为: G( x ) (1 2 x)
n
n 0
sfsf
17
2.1母函数
例 某班有甲乙丙三个小组，人数分别为5，6，9。把5本相同的 书分给甲、乙、丙3个小组，再发到个人手上，每人最多发一本。 考虑将分给某组的某本书发给该组的同学A与将其发给同学B被 认为是不同的分法（每个同学最多一本），而且甲、乙两组最 少1本，甲组最多5本，乙组最多6本，丙组最少2本，最多9本， 问有多少种不同的分配方案？ 解：
5 6 9 4 5 6 9 5 6 9 5 6 9 5 1 1 2 x 1 1 3 1 2 2 2 1 2 x 5 6 9 20 5 6 9 x
sfsf
52
2.3指数型母函数
例、求1，3，5，7，9五个数字组成的n位数的个数（每个数 字可重复出现），要求1、3、7出现的次数一样多，5和9 出现的次数不加限制。求这样的n位数的个数。
sfsf
53
2.3指数型母函数

组合数学第二章081126

组合数学第二章081126
2
1 C (m.1) x C (m.2) x
2
.... C (m.m) x
n m
得：
C(m+n,r )=C(m,0)C(n,r)+C(m,1)C(n,r-1)+…+C(m,r)C(n,0)
第二章 母函数与递推关系
2.1 母函数的引入 同样利用
1 x 1 1/ x
第二章 母函数与递推关系
2.6 指数型母函数 1 问题提出 设有 n 个元素， 其中元素 a1 重复了 n1 次， 元素 a2 重复了 n2 次， …， ... ak 重复了 nk 次，n=n1+n2+ +nk 从中取 r 个排列，求不同的排列数 如果 n1=n2= =nk=1，则是一般的排列问题。 现在由于出现重复，故不同的排列计数便比较复杂。先考虑 n 个 元素的全排列，若 n 个元素没有完全一样的元素，则应有 n!种排列。 若考虑 ni 个元素 ai 的全排列数为 ni! ，则真正不同的排列数为
...
第二章 母函数与递推关系
2.6 指数型母函数 解的分析 先讨论一个具体问题：若有 8 个元素，其中设 a1 重复 3 次，a2 重 复 2 次，a3 重复 3 次。从中取 r 个组合，其组合数为 cr，则序列 c0,c1,c2,c3,c4,c5,c6,c7 的母函数为
从 x 的系数可知，这 8 个元素中取 4 个组合，其组合数为 10。这 10 个组合可从下面展开式中得到
第二章 母函数与递推关系
2.1 母函数的引入
... 定义：对于序列 a0，a1，a1， ，定义 G x a0 a1 x a2 x ... 为序
2
... 列 a0，a1，a1， 的母函数。

§4排列组合与母函数解读

§4排列组合与母函数解读
§4 排列组合与母 函数
一、组合排列的母函数 二、排列数列的母函数
一、组合排列的母
函数
定理
有限数列C{
r n
}（0

n
r

n
）的母函
数为 C(x) (1 x)n
C
r n
x
r
C(x)
r0
. xr
n（1）
r即
的展开式C
r n
0中项r 的n系数为
元
集的元无重组合数 （
）.
例 求证：
(1 x x 2 xmn )
即即 F(x)的展开式 x r 中项的系数为n 元集的r 元
有限重复组合数Fnr 。 例 从3个相同的红球、3个相同的黑球和6个相 同的白球中取8个球，问有多少种不同的取法？
例 设 k 有 个 砝 码 ， 重 量 分 别 为 m1克 、
m2克、……、m
r
①
C
r i m
C
i n

C
r m

n
i0
②
n
rC
r n
n 2 n1
r 1
定理
数列{H
r n
}的母函数为
H (x) (1 x x 2 x k )n
（ 2）
即H (x)的展开中 （x r r 0，1，2，）的系数为 n 元集的
r 元无重组合数。
克（
k
m1，m2
，…
mk ，均为整
数），问在天平上称重量为克的东西共有
多少不同的称法（只允许在天平的一边放
砝码）？
例 求整系数的一次不定方 程2x 3y z 7 的非负整数解的个数。

组合数学 第二章

组合数学 第二章
分 析 : 这 也 是 一 个 有 限 制 条 件 的 组 合 问 题 .即 从 集 合 S = { ∞ ⋅ e1 , ∞ ⋅ e 2 , ∞ ⋅ e 3 } 中 可 重 复 地 选 取 n 个 元 素 , 但 要 求 e1 和 e 2 一 样 多.此 问 题 可 转 化 为 求 集 合 S = { ∞ ⋅ a， ∞ ⋅ b } 的 n可 重 组 合 , 且 a出 现 偶 数 次 .
2 nm
5
展开 式 的 各 项具 有 形 式 ： x k1 x k2 ⋯ x km = x k1 + k2 +⋯+ km
其中x k1 来自第一个因式，x k2 来自第二个因式， ， ⋯
x km 来 自 第 m 个 因 式 ， 且 0 ≤ k i ≤ n， i = 1 2 ⋯ m . ， ， ， i
2 2 2
这表明有5种取球情况 :
(i) 常数项1表示一个球也不取,方案只有1种;
(ii) x + y + z 表示取1个球的取法,方案有3种,分 别为 红 、 黑 、白 三 种 球 只取 1 个; (iii) x 2 + xy + xz + yz 表示取2个球的取法,方案有
,1个 ,1个 4种,分别为2个红球,1个红球1个黑球,1个红球1个白 ,1个 球,1个黑球1个白球;
这6个组合是：
aaabbbbccc， aaabbbcccc， aaabbccccc， aabbbbcccc， aabbbccccc， abbbbccccc
14
例3 设有 2个红球,1个黑球,1个白球.问 : (1) 共有多少种不同的选取方法 ? 试加以枚举. (2) 若每次从中任取3个,有多少种不同的取法?
}的 例 1 求 数 列 {a n } 的 母 函 数 ， 其 中 a n 是 多 重 集 { ∞ ⋅ e1 , ∞ ⋅ e 2 , ⋯ , ∞ ⋅ e k } k + n − 1 的 n可 重 组 合 数 . n

组合数学C2_3_LHRR

组合数学C2_3_LHRR

中 x n 的系数是
A1 A2
n 1
n 2
A1 n (cos i sin ) n A2 n (cos i sin ) n A1 n (cos n i sin n ) A2 n (cos n i sin n ) ( A1 A2 ) cos n i ( A1 A2 ) sin n
• Fibonacci数列
F0 = 0， F1 = 1 ， Fn = Fn - 1 + Fn – 2
Linear Homogeneous Recurrence Relation with constant co-eቤተ መጻሕፍቲ ባይዱficients
定义 如果序列an 满足
C(m) = m2-m-1=(m-)(m-)
拉普拉斯 1812年
似函数,非函数,是映射
伯努利
1705年前
欧拉
递推关系 a n C1a n 1 C 2 a n 2 C k a n k 0,
C ( x ) x k C1 x k 1 C k 1 x C k
整数拆分
1764年前
n n n 母函数G(x)为桥梁 a n l1a1 l 2 a 2 l k a k
a 2 b2
§2.5 线性常系数递推关系 （3）特征多项式 C x 有共轭复根 设 1 , 2 是C x 的一对共轭复根。
A1 A2 1 1 x 1 2 x
1 cos i sin , 2 1 (cos i sin )
C ( x ) x k C1 x k 1 C k 1 x C k
1）特征多项式无重根，k个不同的实数解

组合数学幻灯片43

组合数学幻灯片43
因此序列(a0,a1,…,ar,…)的普通母函数为
1 f ( x ) (1 x x ) 2 1 x
2 4 n
n
n 2 n 1 4 n 2 6 n r 1 2r 1 x 1 x 2 x 3 x r n r 1 2r x r r 0
个不同的物体。显然有三种方法从这三个不 同的物体中选取一个，或者选a，或者选b， 或者选c 我们把这些可能的选取象征性 地记为 a+b+c
同样，从这三个不同的物体中选取两个有三种
方法，或者选取a和b，或者选取b和c，或者选 取c和a。 我们把这些可能选取也象征性 地记为 ab+bc+ca
而从这三个不同的物体中选取三个只 有一种方法，把这种可能的选取象征性地 记为 abc 考虑多项式 (1+ax)(1+bx)(1+cx) =1+(a+b+c)x1+(ab+bc+ca)x2+(abc)x3
对于(1+bx),(1+cx)可作类似的解释。 这样，(1+ax)(1+bx)(1+cx)就表明：对 三个不同的物体a,b,c，其选择方法是， 不选取a或选取a；不选取b或选取b；不 选取c或选取c。
于是这三个因子的乘积中x的幂指数就 表示被选取的物体的个数，而对应的系数 则表明了所有可能的选取方法。
2
r
特别是 ，如果某物体的重复次数是
∞时，则上式的形式变为
2
x x 1 x 2! r!
r
同样地，如果某一物体在排列中至少 取两次，至多取五次，则可用下面的形式 表示
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
精选课件
2.1母函数
例 确定苹果、香蕉、橘子和梨的n-组合的个数，其中在每个n组合中要求：苹果的个数必须是偶数，香蕉的个数必须是5的倍 数，橘子的个数最多4个，梨的个数为0或1个。
解：生成函数为:
G( x) (1 x2 x4 ....)( x0 x5 ....)( 1 x x2 x3 x4 )(1 x)
例 从n双互不相同的五指袜子中取出r只，要求没有任何两只是 成对的，共有多少种不同的取法？

解：生成函数为: G( x) (1 2 x)n C n, r 2r xr n0
精选课件
2.1母函数
例 某班有甲乙丙三个小组，人数分别为5，6，9。把5本相同的 书分给甲、乙、丙3个小组，再发到个人手上，每人最多发一本。 考虑将分给某组的某本书发给该组的同学A与将其发给同学B被 认为是不同的分法（每个同学最多一本），而且甲、乙两组最 少1本，甲组最多5本，乙组最多6本，丙组最少2本，最多9本， 问有多少种不同的分配方案？ 解：
精选课件
2.1母函数
G(
x)


5 i 1

5 i

x
i

6 i 1

6i
xi

9 i2

9 i

x
i



5 1

6 1

9 2

x
4


15
精选课件
2.1母函数
精选课件
2.1母函数
精选课件
2.1母函数
精选课件
2.1母函数
精选课件
2.1母函数
精选课件
2.1母函数
例 设有2个红球，1个黑球，1个白球，问 （1）共有多少种不同的选取方法，试加以枚举？ （2）若每次从中任取3个，有多少种不同的取法？
解：设想用x，y，z分别代表红、黑、白三种球，两个红球的取
G(x)=(1+x2+x4)(x+x3+x5)(x6+x7)(x8+x9)
精选课件
2.1母函数
例 求不定方程k1+k2+k3+k4=20的解数。其中, 限制k1可取0,2,4; k2可取1,3,5; k3可取6,7;k4可取8,9。 G(x)=(1+x2+x4)(x+x3+x5)(x6+x7)(x8+x9)
法与x0，x1，x2对应起来，即红球的可能取法与1＋x＋x2中x的 各次幂一一对应，亦即x0＝1表示不取，x表示取1个红球，x2表 示取两个。对其它球，依此类推。则母函数 G(x,y,z) ＝(1＋x＋x2) (1＋y) (1＋z) ＝1＋(x＋y＋z)＋(x2＋xy＋xz＋yz)＋(x2y＋x2z＋xyz)＋( x2yz)
精选课件
2.1母函数
精选课件
2.1母函数
例 甲、乙、丙3人把n（n≥3）本相同的书搬到办公室，要求甲
和乙搬的本数一样多，问共有多少种分配的方法？
解：G( x) 1 x2 x4 x2k 1 x x2 xk
Cn1 x Cn2 x2


C
n n
xn

1 x
n
精选课件
2.1母函数
例 无限数列{1，1，…，1，…}的普母函数是
1 x x2 xn 1
1 x
例 无限数列{1，2，…，n，…}的普母函数是
1

2x

3
x
2


(n

1)
x
n



(1
1 x)2
精选课件
2.1母函数

1 1 x2
1 1 x5
1 x5 1 x
1
x
1
1 x2


n0
n1 xn
精选课件
2.1母函数
例 从n双互不相同的袜子（每双袜子中的两只相同）中取出r只， 要求没有任何两只是成对的，共有多少种不同的取法？

解：生成函数为: G( x) (1 x)n Cn, r xr n0
= (1+x2+x4) (1+x2+x4)x(1+x)x6(1+x)x8 = (1+x2+x4)2(1+x)2x15 = (1 +x +x2 +x3 +x4 +x5)2x15 只需要多项式(1 +x +x2 +x3 +x4 +x5)2展开式中x5的系数就等于x20 的系数，由多项式定理：C20=6.
16
93


15
62
92


5 2

6 1

9 2
x5Biblioteka 5 5

6 6

9 9

x
20
1080x4 7380x5 x20
母函数及其应用
精选课件
排列组合问题
精选课件
2.1母函数
定义2.1.1 对于数列{an}，称无穷级数

Gx an xn n0
为该数列的（普通型）母函数，简称普母函数或母函数。同时称
{an}为G(x)的生成数列。
例 有限数列C(n,r)，r＝0,1,2, …,n的普母函数是
Cn0
由x3的系数即得所求方案数为3。
精选课件
2.1母函数
例 求不定方程k1+k2+k3+k4=20的解数。其中, 限制k1可取0,2,4; k2可取1,3,5; k3可取6,7;k4可取8,9。 解：设不定方程k1+k2+k3+k4=k的解组数目为ck，本例中m=4, k=20。 注意到对ki(i=1,2,3,4)的限制，序列{ck}对应的生成函数为:
精选课件
2.1母函数
例 求不定方程3k1+4k2+2k3+5k4=n的非负整数解的个数。
g(x) (1 x3 x6 ....)(1 x4 x8 ...) (1 x2 x4 ....)(1 x5 x10 ...) 1111 1 x3 1 x2 1 x4 1 x5
若令x＝y＝z＝1，就得所有不同的选取方案总数为 G(1,1,1) ＝1＋3＋4＋3＋1＝12
精选课件
2.1母函数
例 设有2个红球，1个黑球，1个白球，问 （1）共有多少种不同的选取方法，试加以枚举？ （2）若每次从中任取3个，有多少种不同的取法？ 解：若只考虑每次取3个的方案数，而不需枚举，则令y＝x，z ＝x，便有 G(x) ＝ (1＋x＋x2) (1＋x) (1＋x) ＝ 1＋3x＋4 x2＋3 x3＋ x4