第九章影响线及其应用资料
- 格式:ppt
- 大小:1.31 MB
- 文档页数:37

1§9-7 影响线的应用9 利用影响线求固定荷载作用下的某量值大小9 确定移动荷载的最不利位置利用影响线计算量值绘制影响线时,考虑的是单位荷载FP=1 的作用。
当若干具体荷载作用于结构时,可根据叠 加原理,利用影响线计算出该内力所受的总影 响,即产生的该内力总值称之为影响量。
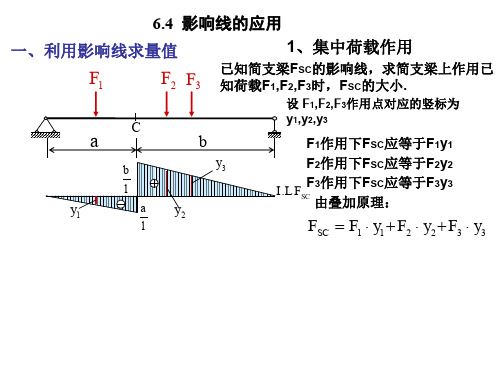
2(1)一组集中荷载作用下的影响FP1 FP2 FP3 FPn3y1y2 y3 ynS影响线由FP1产生的S 值等于 FP1 ⋅ y1 由FP2产生的S 值等于 FP2 ⋅ y2 FP1、FP2、…、FPn共同作用下S 的数值为:S = FP1 ⋅ y1 + FP 2 ⋅ y2 + FP 3 ⋅ y3 L FPn ⋅ yn简化计算当若干个荷载作用在影响线某一段直线的 范围内时,可用它们的合力来代替。
FR F FP1 FP2 FP i Pn4αy1 xiy2y yiynS影响线S = FP1 ⋅ y1 + FP 2 ⋅ y2 + FP 3 ⋅ y3 Λ FP n ⋅ yn= ∑ FP i ⋅ yi = ∑ FP i ( xi ⋅ tgR α ) = tg α ∑ FP i xiS=F ⋅y(2)均布荷载作用下的影响q a x qdx b dx y S影响线5在均布荷载作用段上,将微段dx上的荷载qdx看 作一个集中荷载,则它引起的S 的量值为qdx · y。
在ab段均布荷载产生的S 的值为:b b bS = qAa aS =∫ qdx ⋅ y = q ∫ y ⋅ dx = q ∫ dA = qAa6工程中常见的荷载有集中荷载和均布荷载FP1 FP2 q FP3yi 和 A 是代数量y3⊕ y2\nA \ y 1m由叠加原理S = ∑ FP i yi + ∑ q j A ji =1 j =1例:利用影响线求图示梁K截面的弯矩100kN7K100kN 50kN/m↓↓↓↓↓↓ ↓↓↓↓↓↓↓↓↓ ↓↓↓↓↓↓↓↓↓ ↓↓↓↓↓↓30kN/m30kN.m6m3m 3m 3m 4 6 5 46m A1 26m A23m A3 1I.L.MK (m)MK=P1y1+ P2y2 +q1A1+q2(A2- A3)+mtgθ=100×4+100×5+50 × 18+30× 6-30 × 1.5 -30×1/3 =1925kN.m中—活载(普通活载)8车头煤水车车箱中—活载(普通活载)9使用中一活载时,可由图式中任意截取,但不得 变更轴距。




1第九章 影响线及其应用移动荷载与影响线的概念2目的:解决移动荷载作用下结构的内力计算问题。
内容:1)在移动荷载作用下结构内力变化规律和范围;2)确定内力的最大值及相应的荷载位置——最不利荷载位置。
方法:在各种荷载中抽象出单位荷载(FP =1)。
利用平衡条件建立影响线方程:FP=1xFP=1FR B=x lFP=x (0l≤x≤l)lx = l , l , 3l , l4 24y1FRB = 0.25, 0.5, 0.75, 10.25 0.5FRB的影响线(I . L)-Influence LineFP1y20.75 FP23FR B1.0影响线的应用例:FRB = FP1 ⋅ y1 + FP2 ⋅ y2lFR B定义:当单位荷载(FP=1)在结构上移动时,表示结构某一量值变化规律的图线,称为该量值的影响线。
定义:当单位荷载(FP=1)在结构上移动时,表示结构某一量 4 值变化规律的图线,称为该量值的影响线。
FP=1FP=1DFRBy=FRB1+yDxFRB影响线影响线基线5在绘影响线时,反映FP=1的作用范围, 垂直于FP=1的直线称为基线。
通常规定其量值为正值的竖标画在基线的上 方,反之,画在基线的下方,影响线要标明符号。
I . L. FRB1基线无论是研究结构在移动荷载作用下的内力变化规律或最 6 不利荷载位置,内力影响线都是最基本的工具。
影响线有两种画法;静力法和机动法。
xAF RA1FP=1 l静力法作静定梁的影响线B (1)FRA∑MB = 0FFRA ⋅l −1⋅(l − x) = 0RBFR A=l− lx,(0 ≤ x ≤ l)I.L.FRA (2)FRB∑MA =01FR B=x lP=x l(0≤x≤l)I.L.FRB作简支梁C截面的弯矩影响线、剪力影响线 7FP=1AxCBabl正负号规定:支反力以向上为正;弯矩以梁的下侧纤 维受拉为正;剪力以沿截面产生顺时针转动方向为正FP=1Ax FAy aMC MCBFQC FQC b FBy作I . L . MCxFP=1Ca lbMC C FQCb当FP=1在C之左移动 8由 ∑MC = 0,MC = FRB ⋅ b = x ⋅ b (0 ≤ x ≤ a) lB左直线方程 FRB当FP=1在C之右移动 9xFP=1Cal由 ∑ MC = 0,AFRA aCMCFQC.MC = FRA ⋅ a = l − x ⋅a (a ≤ x ≤ l) l右直线方程绘出I . L . MC左直线方程10FP=1aClMC = FRB ⋅ b = x ⋅b l (0 ≤ x ≤ a)右直线方程MC = FRA ⋅ aaab/l左直线b右直线+= l − x ⋅a l(a ≤ x ≤ l)I . L . MC简支梁C截面的剪力影响线11xFP=1Ca当FP=1在C之左移动由 ∑ Fy = 0,lMC C FQCFQC=−FRB=−x lB(0 ≤ x ≤ a)FRB 左直线方程当FP=1在C之右移动 12xFP=1C由 ∑ Fy = 0 ,a lA FRAC MC FQCFQC=FRA=l− lx(a ≤ x ≤ l)右直线方程绘出I . L . FQCFP=1aCl13左直线方程FQC=−FRB=−x l(0 ≤ x ≤ a)1 左直线I . L . FQC右直线方程b/l右直线+ -FQC=FRA=l− lx(a ≤ x ≤ l)a/l1内力影响线与内力图的比较14FP=1FPA lBabbll1FPbalabalI . L . FQC1bI . L . MClFP aFQlMFPab影响线内力图 l荷载大小 荷载性质FP=1 移动实际 固定横座标表示荷载位置表示截面位置纵座标 表示某一截面内力变化规律 表示全部截面内力分布规律悬臂梁的影响线15求MC 、FQC 、 MA、FQA的影响线FP=1悬臂梁MC 、FQC的影响线16FP=1当FP=1在AC段移动时:左直线MC = 0 FQC = 0当FP=1在CB段移动时:MCxFP=1x右直线FQC MC =- x FQC = 1悬臂梁MC 、FQC的影响线171左直线-+右直线I . L . MC bI . L . FQC悬臂梁MA 、FQA的影响线18-I . L . MA l1+I . L . FQA。
第一节影响线概念一般工程结构除了承受恒载外,还将受到活载的作用。
吊车梁要承受吊车荷载(图9-1),桥梁要承受汽车、火车荷载等。
在进行结构设计时,需要算出结构在恒载和活载共同作用下各量值的最大值。
就需要研究活载作用下结构各量值的变化规律,以便找出它们的最大值。
图9-1结构在活载作用下的计算,从原理上讲与前述静力计算无异,只是荷载位置不是固定的。
显然,要求出活载作用下某一量值的最大值,必须先确定产生这种最大值的荷载位置。
这一荷载位置称为该量值的最不利荷载位置。
在寻求最不利荷载位置时,由于结构上各量值的变化规律并不相同,因此只能逐一考虑。
例如:(图9-2a)所示的简支梁,当有一汽车自左向右移动时,各截面的内力和支座反力等都将随荷载的移动而变化(图9-2b)。
其中,左支座反力FAy是逐渐减小的;相反,右支座反力FBy 的变化却是逐渐增大的。
可见FAy和FBy的变化规律是不同的,因而它们的最不利荷载位置也是不同的。
图9-2在实际工程中,活载又可分为移动活载和可动活载两类。
汽车荷载吊车荷载都属移动荷载,而人群、风、雪等活载则属可动活荷载。
=1移动为了清晰和直观起见,最好把量值随FP而变化的规律用函数图形表示出来,这种图形称为影响线。
它的定义如下:当一个方向不变的单位荷载沿一结构移动时,表示某指定截面的某一量值变化规律的函数图形,称为该量值的影响线。
图9-3a 所示的简支梁,其支座A 的反力F Ay 的影响线(图9-3b)的竖标分别表示F P =1作用于A 、C 、…、B 各点时,反力F Ay 的大小。
显然,F Ay 的影响线只能表示F P =1在梁上移动时F Ay 的变化规律。
如果要表示F By 或其它量值的变化规律,则需另行作出F By 的影响线或其它相应量值的影 、 、 、 B Ay C Ay A Ay F F F F P =14l 4l 4l 4l F Ay F By E A B C D 1=A Ay F 43=C Ay F 21=D Ay F 41=E Ay F 0=B AyF F Ay 影响线(a)(b)图9-3影响线是研究活载作用下结构计算的基本工具。