奈奎斯特稳定判据
- 格式:ppt
- 大小:1.43 MB
- 文档页数:46



奈奎斯特稳定判据及应用奈奎斯特稳定判据是一种用于分析线性时不变系统稳定性的常用方法。
该方法的基本思想是通过对系统的频率响应进行分析,判断系统的稳定性。
下面我将详细介绍奈奎斯特稳定判据及其应用。
奈奎斯特稳定判据是由德国数学家埃尔温·奈奎斯特(Ernst Siegfried H Stabilization)在20世纪20年代提出的。
该判据基于系统的开环频率响应曲线和频率扰动的关系,通过分析系统的极点和奈奎斯特曲线的特性来判断系统的稳定性。
在分析一个系统的稳定性时,首先需要了解系统的传递函数。
传递函数是描述系统输入和输出之间关系的数学模型,通常表示为H(s),其中s是复频率。
传递函数中的极点(也称为极值)是指使传递函数无穷大的复频率值。
对于线性时不变系统,只有当所有的极点都位于s平面的左半平面时,系统才是稳定的。
根据奈奎斯特稳定判据,一个线性时不变系统是稳定的,当且仅当奈奎斯特曲线上的点环绕虚轴的次数等于系统极点位于虚轴右侧的个数。
这可以通过两个主要步骤来实现。
首先,我们需要绘制系统的开环频率响应曲线。
开环频率响应曲线是指系统传递函数H(s)的模量和幅角随频率变化的曲线。
我们可以通过画出传递函数的特定频率响应曲线来获得。
其次,我们需要绘制奈奎斯特曲线。
奈奎斯特曲线是通过将开环频率响应曲线绕过s 轴上方的点连接而得到的曲线。
具体来说,奈奎斯特曲线的性质如下:- 如果系统的开环频率响应曲线没有通过-1+j0(虚轴上的-1点),则奈奎斯特曲线将通过-1+j0;- 如果系统的开环频率响应曲线通过-1+j0,但未环绕虚轴上的任何点,则奈奎斯特曲线将通过-1+j0;- 如果系统开环频率响应曲线经过-1+j0,并绕过了虚轴上的n 个点,则奈奎斯特曲线将通过-1+j0并绕过虚轴上的n 个点。
通过绘制奈奎斯特曲线,我们可以根据它的形状和特性判断系统的稳定性。
奈奎斯特稳定判据的应用广泛,尤其在控制系统设计和分析方面。



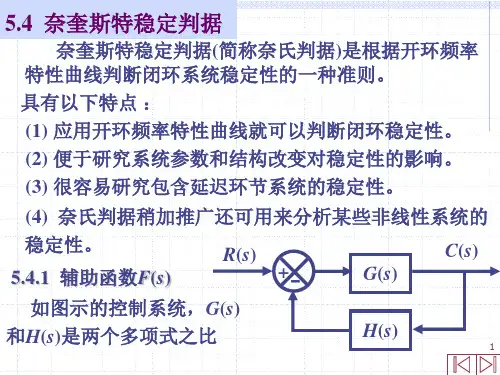




奈奎斯特稳定判据例题奈奎斯特稳定判据是用于判断线性时不变系统的稳定性的一种方法。
它基于系统的开环传递函数,通过绘制奈奎斯特曲线来分析系统的稳定性。
下面我将给出一个奈奎斯特稳定判据的例题,并从多个角度进行详细解答。
例题,考虑一个开环传递函数 G(s) = (s+1)/(s^2+2s+2) ,判断该系统的稳定性。
解答:1. 奈奎斯特曲线的绘制:首先,我们需要将开环传递函数 G(s) 转化为极坐标形式。
对于 G(s) = (s+1)/(s^2+2s+2) ,我们可以将其写成G(jω) =(jω+1)/((jω)^2+2(jω)+2) 的形式,其中 j 是虚数单位,ω 是频率。
然后,我们可以根据频率范围来绘制奈奎斯特曲线。
通常,我们会从频率为零开始,逐渐增加频率到无穷大。
在每个频率点上,计算G(jω) 的幅度和相位,并将它们绘制在复平面上。
最后,我们得到奈奎斯特曲线。
2. 奈奎斯特曲线的判据:奈奎斯特稳定判据基于奈奎斯特曲线的形状来判断系统的稳定性。
根据奈奎斯特曲线的特点,我们可以得出以下结论:如果奈奎斯特曲线不经过虚轴右半平面的任何点,那么系统是稳定的。
如果奈奎斯特曲线经过虚轴右半平面的点的个数与闭环极点的个数相等,且没有穿过虚轴,那么系统是边界稳定的。
如果奈奎斯特曲线经过虚轴右半平面的点的个数多于闭环极点的个数,那么系统是不稳定的。
3. 应用奈奎斯特稳定判据:对于给定的例题 G(s) = (s+1)/(s^2+2s+2) ,我们可以根据上述奈奎斯特曲线的判据来判断系统的稳定性。
首先,我们需要绘制奈奎斯特曲线。
根据开环传递函数 G(s)的极点,我们可以得知该系统的极点为 -1+j 和 -1-j 。
因此,奈奎斯特曲线应该经过虚轴右半平面的两个点。
然后,我们可以根据奈奎斯特曲线的形状来判断系统的稳定性。
如果奈奎斯特曲线没有穿过虚轴,那么系统是稳定的。
如果奈奎斯特曲线穿过虚轴,那么系统是不稳定的。
绘制奈奎斯特曲线后,我们发现奈奎斯特曲线没有穿过虚轴,而是经过虚轴右半平面的两个点。