夹逼定理练习
- 格式:doc
- 大小:263.39 KB
- 文档页数:2

夹逼法例题【原创版】目录1.夹逼法的定义和概念2.夹逼法的应用范围和条件3.夹逼法的解题步骤和方法4.夹逼法的例题解析5.夹逼法在实际问题中的应用正文一、夹逼法的定义和概念夹逼法,又称为夹逼定理,是一种求极限的方法。
它是通过构造两个函数,分别从左右两侧逼近目标函数,通过比较这两个函数的极限值,得到目标函数的极限值。
夹逼法广泛应用于数学分析、物理学和经济学等领域。
二、夹逼法的应用范围和条件夹逼法适用于求解以下类型的问题:1.求函数在某一点的极限值;2.求解无穷小量和无穷大量;3.求解连续函数的值域。
应用夹逼法的条件:1.两个函数在给定区间内连续;2.两个函数在给定区间内单调;3.两个函数在给定区间内的极限值存在且相等。
三、夹逼法的解题步骤和方法1.构造两个函数,分别从左右两侧逼近目标函数;2.证明这两个函数在给定区间内连续、单调;3.求出这两个函数在给定区间内的极限值;4.比较这两个函数的极限值,得到目标函数的极限值。
四、夹逼法的例题解析例题:求函数 f(x) = sinx / x 在 x 趋近于 0 时的极限值。
解:构造两个函数 g(x) = sinx 和 h(x) = 1 / x,分别从左右两侧逼近目标函数 f(x)。
1.证明 g(x) 和 h(x) 在区间 (-∞, 0) 和 (0, +∞) 内连续、单调;2.求出 g(x) 和 h(x) 在区间 (-∞, 0) 和 (0, +∞) 内的极限值,分别为 -1 和+∞;3.比较 g(x) 和 h(x) 的极限值,得到 f(x) 在 x 趋近于 0 时的极限值为 -1。
五、夹逼法在实际问题中的应用夹逼法在求解实际问题中的应用非常广泛,如求解物理学中的电磁场问题、经济学中的边际效用等。

夹逼定理例题夹逼定理,也称作中值定理,是一种经典定理,由美国数学家卢伊兹夹尔在1885年提出。
它被用来证明一个函数在一个闭区间上是单调的。
英文原版称之为Intermediate Value Theorem,即「中值定理」。
夹逼定理的数学证明夹逼定理的定义如下:设f(x)为区间[a,b]上的连续函数,若存在实数c,使得f(a)<c<f(b),则存在x∈[a,b],使得f(x)=c。
证明如下:因为f(x)是[a,b]上的连续函数,所以f(x)在[a,b]上是一个闭区间,由定理可知,闭区间上的连续函数是有定界的,即f (a) m f (b)设f (a) < c < f (b) 且f (c) = k由于f (x)是连续函数,可以令f (a) < m 且 m < c此时,根据闭区间上的连续函数是有定界,存在实数x,使得 f(x)≤k,且x∈[a,c]同理可以知道f(x)≥k,且x∈[c,b]由于f (a) < c < f (b)并且f (c) = k所以f (x)的定义域是[a,b],其值域为[f (a),f (b)]由此得到f(x)=k,其中x∈[a,b]综上,得证。
夹逼定理的应用夹逼定理在数学中用于证明一个函数在一个闭区间上是单调的,即在闭区间上存在唯一的解。
它也可以帮助解决积分问题。
因为,给定一个函数,可以根据它在闭区间上的单调性来求解积分。
夹逼定理在随机变量的分布曲线中也有应用,给定概率密度函数f(x),在一个闭区间[a,b]上,只要满足夹逼定理的条件,就可以证明随机变量X的分布曲线在[a,b]上是单调的。
夹逼定理的例题例1:证明函数f(x)=x2+2x-2在区间[-2,2]上是单调的解:由夹逼定理可知,若f(x)在[a,b]上是单调的,则必须满足f(a)≤m≤f(b)我们考虑函数f(x)=x2+2x-2,在[-2,2]上,f(-2)=-2+2(-2)-2=-8f(2)=2+2×2-2=2由此可以知道f(-2)<m<f(2),而且f(x)在[-2,2]上是连续函数,因此可以满足夹逼定理的要求,故f(x)=x2+2x-2在区间[-2,2]上是单调的。

第六节 夹逼定理 无穷小的比较一. 夹逼定理定理1:如果数列{}n x 、{}n y 及{}n z 满足下列条件:(1)n n n z x y ≤≤,(Λ,3,2,1=n )。
(2) a y n n =∞→lim ,a z n n =∞→lim 。
则数列{}n x 的极限存在,且a x n n =∞→lim 定理2:设函数)(x f 在点a 的的某一去心邻域),(δ∧a U 内(或X x ≥时) 满足条件:(1))()()(x h x f x g ≤≤。
(2) A x g a x =→)(lim ,A x h a x =→)(lim (或A x g x =∞→)(lim ,A x h x =∞→)(lim )。
则)(lim x f a x →存在,且A x f a x =→)(lim ((或)(lim x f x ∞→存在,且A x f x =∞→)(lim )。
注:(1)夹逼定理不仅说明了极限存在,而且给出了求极限的方法。
(2) 定理1中的条件(1)改为:n n n z x y ≤≤,(Λ,3,2,1=n ),结论仍然成立。
例1: 求下列极限(1)n n n 11lim +∞→ (2))1...2111(lim 222nn n n n ++++++∞→ 二.两个重要极限(1)1sin lim 0=→xx x 。
(2)e x x x =+∞→)11(lim ,(e x x x =+→10)1(lim ,e nn n =+∞→)11(lim )。
例2:求下列极限(1) x x x tan lim 0→ (2) 30sin tan lim xx x x -→(3)203cos cos lim x x x x -→ 例3:求下列极限(1) x x x 2)21(lim -∞→ (2) 212)2(lim -→x x x (3)x x x x )55(lim -+∞→三. 无穷小的比较在极限的运算法则中,我们讨论了两个基本点无穷小的和、差及乘积仍是无穷小。

第二章习题2-11. 试利用本节定义5后面的注(3)证明:若lim n →∞x n =a ,则对任何自然数k ,有lim n →∞x n +k =a .证:由lim n n x a →∞=,知0ε∀>,1N ∃,当1n N >时,有取1N N k =-,有0ε∀>,N ∃,设n N >时(此时1n k N +>)有 由数列极限的定义得 lim n k x x a +→∞=.2. 试利用不等式A B A B -≤-说明:若lim n →∞x n =a ,则lim n →∞∣x n ∣=|a|.考察数列x n =(-1)n ,说明上述结论反之不成立. 证:而 n n x a x a -≤- 于是0ε∀>,,使当时,有N n N ∃>n n x a x a ε-≤-< 即 n x a ε-<由数列极限的定义得 lim n n x a →∞=考察数列 (1)nn x =-,知lim n n x →∞不存在,而1n x =,lim 1n n x →∞=,所以前面所证结论反之不成立。
3. 利用夹逼定理证明:(1) lim n →∞222111(1)(2)n n n ⎛⎫+++ ⎪+⎝⎭=0; (2) lim n →∞2!nn =0.证:(1)因为222222111112(1)(2)n n n n n n n n n n++≤+++≤≤=+ 而且 21lim0n n →∞=,2lim 0n n→∞=,所以由夹逼定理,得222111lim 0(1)(2)n n n n →∞⎛⎫+++= ⎪+⎝⎭. (2)因为22222240!1231n n n n n<=<-,而且4lim 0n n →∞=,所以,由夹逼定理得4. 利用单调有界数列收敛准则证明下列数列的极限存在. (1) x n =11n e +,n =1,2,…;(2) x 1x n +1,n =1,2,…. 证:(1)略。


6.1(3.1)算术平方根--夹逼法一.【知识要点】1.可以用夹逼法求一个含根号的无理数的近似值。
二.【经典例题】1.已知m=34+,则以下对m 的估算正确的是( ) A 2<m<3 B 3<m<4 C 4<m<5 D 5<m<62.国际比赛的足球场长在100m ~110m 之间,宽在64m ~75m 之间,现有一个长方形的足球场,其长是宽的1.5倍,面积是75602m ,问:这个足球场能用来进行国际比赛吗?3.若a,b 均为正整数,且a>7,b>22,则a+b 的最小值是( )A 3B 4C 5D 64.已知x 是整数,当x 取最小值时,x 的值是( )A .5B .6C .7D .8三.【题库】【A 】1.下列各数中,界于6和7之间的数是( ) A.28 B.43 C.58 D.392.一个正方形的面积是15,估计它的边长大小在( )A .2与3之间B .3与4之间C .4与5之间D .5与6之间【B 】1.估计18+的值在( )A 2到3之间B 3到4之间C 4到5之间D 5到6之间2.若两个连续整数y x ,满足y x <+<15,则y x +的值是___________3.怎样计算边长为1的正方形的对角线的长?11【C】1.(1)如图1,小明想剪一块面积为252cm的正方形纸板,你能帮他求出正方形纸板的边长吗?(2)若小明想将两块边长都为3cm的正方形纸板沿对角线剪开,拼成如图2所示的一个大正方形,你能帮他求出这个大正方形的面积吗?它的边长是整数吗?若不是整数,那么请你估计这个边长的值在哪两个相邻整数之间?【D】。


夹逼法求函数极限经典例题在初中数学中,函数极限经常作为一个常考概念出现。
如果求出函数极限时,你使用哪些方法呢?如果你能熟练运用夹逼法就能轻松解决。
夹逼法是函数极限学习中的一个重要方法。
夹逼法主要是利用函数的相关性质求解函数的极限。
所谓的夹逼法就是在掌握公式的前提下,使用一种特殊的夹逼法,通过夹住函数的某一元素或者函数一阶极限区域上的一个点来达到求解函数极限的目的。
本例例中求解函数极限就是利用了夹逼法的运算法则来求出某一元素或者函数上限区域上的一个点,所以我们可以说该类型题是一种典型的夹逼法求极限例题。
首先要说明一下夹逼法计算函数的极限并不是很困难的运算法则哦,主要是借助夹逼法可以得到函数的极限条件!所以当你学会夹逼题也会很轻松就能计算出函数极限区域上的一个点了!一、例题(模拟题)解:由定义可知, f (x)在坐标轴上的坐标为 x+1,函数的 f (x)的值在该坐标轴上最大值为1 (即 f (x)在坐标轴上的值为 a-1)’=x-1/n+2,由式中可以看出 f (x)的值不会大于1。
设函数 f (x)在 x轴上的最大最小值为1.分析:此题中,要求函数 f (x)在坐标轴上的最大值不小于2.由于 f (t)为一个连续 n阶数,故在坐标轴上唯一确定的是 t+2.因此,利用夹逼法可得到函数极限区的所有解中,只要 t>0即可得出极限区域上任何一个点可以包含两个素数。
因此正确答案是: a-1/2= b-1/3=0.因此 c为函数 f (x-3)在坐标轴中最大值。
解:请将原函数 f (x-3)分解成为函数 g 0、 g=2、 N 1四个解析式。
运用夹逼法能得出以下结论:此方法适合于复杂的数学题时,如直线解方程,圆解方程.当然这里要说明的是本例中使用夹逼法求极限区域上任意一个点都可以。
但在计算时一定不能仅考虑到变量间相互影响而是考虑到变量间相互独立性和对变量间相互影响。
所以要注意以下几点:求解极限区间及边界条件:首先我们要明确一点,函数有多个值之和时,若求出函数在某一个区间对应的一个极限可以省略某些值或直接将极限区间写成整数是不可行的。

夹逼定理例子《夹逼定理例子:数学里的“左右为难”》嘿,朋友们!今天咱来聊聊数学里特别有意思的一个玩意儿——夹逼定理!这名字听着就有点儿喜感,好像什么东西被夹在中间,左右为难似的。
咱先说说夹逼定理是啥玩意儿哈。
简单来说呢,就是如果有两个函数把另一个函数夹在中间,而且这两个家伙在某个地方的极限是一样的,那被夹的那个函数的极限也就确定了。
听着是不是有点晕乎?别急,让我给你举个接地气的例子。
想象一下哈,你站在一条窄窄的胡同里,左边有个大汉一步一步地逼近你,右边也有个大汉同样一步一步地靠近你。
这时候你是不是感觉自己被“夹逼”啦?而且如果这俩大汉最后都走到了同一个位置,那就相当于这两个函数的极限相同了。
我记得当初学夹逼定理的时候,看到那些题目就感觉像是在看一场有趣的“挤压游戏”。
比如说,有个题目让我们求某个复杂式子的极限,然后我们就开始找能把它夹住的那两个函数。
这就好比我们要给那个式子找两个“保镖”,让它们左右保护着。
有时候找起来可不容易呢,就像在茫茫人海中找两个合适的保镖一样。
有一次,老师在黑板上出了一道题,看着那复杂的式子,我们都傻眼了。
这可咋办呢?大家都开始绞尽脑汁地想怎么给它找“保镖”。
突然,有个同学大喊一声:“我找到了!”大家都投去敬佩的眼光,心想这家伙也太牛了吧。
然后老师一看,嘿,还真对!这感觉就像是在一堆乱麻中找到了线头,一下子就把问题给解开了。
夹逼定理还让我想起了生活中的一些场景。
比如说,你答应了妈妈晚上要早点回家,但是朋友们又约你去玩。
这不就是被夹在中间了嘛!左边是妈妈的期待,右边是朋友的邀请,真是左右为难啊。
这时候你就得权衡一下,看看怎么才能找到那个最合适的选择,就像用夹逼定理去求解极限一样。
总的来说,夹逼定理虽然名字听着挺搞笑,但却是数学里非常有用的一个工具。
它让我们学会了在复杂的情况下找到突破口,用巧妙的方法求出那些看似很难的极限。
而且通过它,我们还能在生活中找到很多类似的情景,让我们更加善于思考和决策。
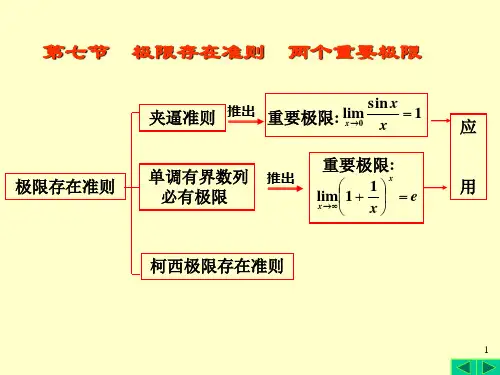

夹逼定理,也称两边夹定理、夹逼准则、夹挤定理、挟挤定理、三明治定理,是判定极限存在的两个准则之一,是函数极限的定理。
定义,一.如果数列{Xn},{Yn}及{Zn}满足下列条件:(1)当n>No时,其中No∈N*,有Yn≤Xn≤Zn,(2)当n→+∞,limYn =a;当n→+∞ ,limZn =a,那么,数列{Xn}的极限存在,且当n→+∞,limXn =a。
证明.,因为limYn=a limZn=a 所以根据数列极限的定义,对于任意给定的正数ε,存在正整数N1,N2,当n>N1时,有〡Yn-a∣﹤ε,当n>N2时,有∣Zn-a∣﹤ε,现在取N=max{No,N1,N2},则当n>N时,∣Yn-a∣<ε,∣Zn-a∣<ε同时成立,且Yn≤Xn≤Zn,即a-ε<Yn<a+ε,a-ε<Zn<a+ε,有a-ε<Yn≤Xn≤Zn<a+ε,即∣Xn-a∣<ε成立。
也就是说limXn=a二.函数的夹逼定理F(x)与G(x)在Xo连续且存在相同的极限A,即x→Xo时, limF(x)=limG(x)=A则若有函数f(x)在Xo的某邻域内恒有F(x)≤f(x)≤G(x)则当X趋近Xo,有limF(x)≤limf(x)≤limG(x)即A≤limf(x)≤A故limf(Xo)=A简单的说:函数A>B,函数B>C,函数A的极限是X,函数C的极限也是X ,那么函数B的极限就一定是X,这个就是夹逼定理.应用1.设{Xn},{Zn}为收敛数列,且:当n趋于无穷大时,数列{Xn},{Zn}的极限均为:a.若存在N,使得当n>N时,都有Xn≤Yn≤Zn,则数列{Yn}收敛,且极限为a.2.夹逼准则适用于求解无法直接用极限运算法则求极限的函数极限,间接通过求得F(x)和G(x)的极限来确定f(x)的极限。
我们要通过夹逼法来证明一个数列的极限。
首先,我们要理解什么是夹逼法。
夹逼法是一种通过比较数列的上界和下界来证明数列极限的方法。
如果一个数列的上界和下界都收敛到同一个值,那么这个数列也一定收敛到这个值。
假设我们有一个数列a_n,我们想要证明它的极限是A。
首先,我们需要找到这个数列的上界和下界。
上界可以表示为b_n,下界可以表示为c_n。
如果b_n 和c_n 都收敛到A,那么a_n 也一定收敛到A。
现在我们有一个具体的例子来演示如何使用夹逼法。
假设我们有一个数列a_n = 1/n^2,我们想要证明它的极限是0。
首先,我们找到这个数列的上界和下界。
上界可以表示为b_n = 1/n,下界可以表示为c_n = 0。
现在我们要证明b_n 和c_n 都收敛到0。
对于上界b_n = 1/n,我们可以使用夹逼法来证明它收敛到0。
我们知道1/n > 1/(n+1),所以b_n > 1/(n+1)。
由于1/(n+1) 收敛到0,所以b_n 也收敛到0。
对于下界c_n = 0,它已经直接收敛到0。
现在我们已经证明了a_n 的上界和下界都收敛到0,所以a_n 也收敛到0。
夹逼准则三角函数题
夹逼准则是解决极限问题中常用的一种方法,它在三角函数题中也有广泛的应用。
三角函数题通常涉及到求极限或者证明恒等式等问题,下面我将从不同角度来讨论夹逼准则在三角函数题中的应用。
首先,夹逼准则在三角函数题中常常用来解决求极限的问题。
例如,当我们需要求解sin(x)/x在x趋于0时的极限时,可以利用夹逼准则,构造一个夹在sin(x)/x和1之间的函数,从而利用夹逼准则得出sin(x)/x的极限为1。
类似地,对于其他三角函数的极限问题,夹逼准则也可以提供一种简洁而有效的解决方法。
其次,夹逼准则在证明三角函数恒等式中也有重要的应用。
例如,我们需要证明tan(x) + sin(x)/cos(x) = sec(x)时,可以利用夹逼准则构造一个夹在tan(x) + sin(x)/cos(x)和sec(x)之间的函数,从而利用夹逼准则来证明该恒等式成立。
通过巧妙地选择夹逼函数,可以简化证明过程,提高证明的效率。
此外,夹逼准则还可以在三角函数题中帮助我们理解函数的性质。
通过分析夹逼过程中夹逼函数与原函数的关系,我们可以更深
入地理解三角函数的性质,例如它们的增减性、周期性等特点。
这有助于我们更好地掌握三角函数的性质和应用,提高解决问题的能力。
综上所述,夹逼准则在三角函数题中具有重要的应用价值,不仅可以用来解决极限问题,还可以用来证明恒等式和帮助理解函数的性质。
通过熟练掌握夹逼准则的应用方法,我们可以更加灵活地解决三角函数题,提高数学问题解决能力。
1、设数列{an} 满足a1 = 1,且an+1 - an = 1/(n(n + 1)),则数列{an} 的通项公式为A. an = n/(n + 1)B. an = (n + 1)/nC. an = n/(n - 1)D. an = (n - 1)/n(答案)A2、已知x > 0,y > 0,且3x + 2y = xy,若2x + 3y > t2 + 5t + 1 恒成立,则实数t 的取值范围是A. (-10, -2)B. (-8, 1)C. (-∞, -8) ∪(1, +∞)D. (-∞, -2) ∪(10, +∞)(答案)C3、设函数f(x) = (x - a)/(ex),a ∈ ℝ,若x₁ < x₁且f(x₁) = f(x₁),则a(x₁ + x₁) 的取值范围是A. (0, 2)B. (2, +∞)C. [2, +∞)D. (0, +∞)(答案)A4、已知数列{an} 的前n 项和为Sn,且Sn = 2 - 2an (n ∈ N*),若不等式log2(a₁₁₁/a₁) < m 对任意的n ∈ N* 恒成立,则实数m 的取值范围是A. [1, +∞)B. (1, +∞)C. (-∞, 1)D. (-∞, 1](答案)D5、已知函数f(x) = (x + 1 - a)/(ex) (a ∈ ℝ) 的图象在点(0, f(0)) 处的切线为l,若l 的斜率为-2,则a 的值为A. -2B. -1C. 1D. 3(答案)D6、若x₁,x₁是函数f(x) = (1/3)x³ - x² + 2x - a 的两个极值点,且|x₁ - x₁| = 2,则实数a =A. -2B. -1C. 1D. 2(答案)B7、已知函数f(x) = ex - ax - 1 (a ∈ ℝ).(1) 若函数f(x) 在ℝ上单调递增,求a 的取值范围;(2) 若函数f(x) 有两个不同的零点x₁,x₁ (x₁ < x₁),且不等式f(x₁) + f(x₁) < 0 成立,求a 的取值范围.A. a > 1B. 0 < a < 1C. a < 0D. a > 2(答案)A;D8、已知x > 0,y > 0,lg2x + lg8y = lg26,则1/x + 1/y 的最小值为A. 1/4B. 4C. 1/2D. 9/2(答案)C。
利用夹逼原则求极限之杨若古兰创作夹逼原则的使用方法:定理1 用夹逼原则求极限,就是将数列放大和缩小.请求放大和缩小后的极限容易求出,此时常将其放大到最大项的整数倍,缩小到最小项的整数倍,而且此时两者极限相等,即两者是等价无量小,此时就可以得到原数列极限的值.题型1 夹逼原则经常使用于求若干项和的极限推论1 极限变更过程中最小项与最大项之比为1时可以使用夹逼原则求其极限.证实:不妨设最小项为)(x α,最大项为)(x β,数列有n 项,则整数倍为n 倍, 由定理1可知.)()(lim 1)()(limx x x n x n βαβα==)21 (4)121(lim 222nn n n n ++++++∞→.解:.11lim 22lim 22lim 2121lim 222222==++=++=++∞→∞→∞→∞→n n n n n n n nn n n n n由推论1,.1221 (4)1212122222→+≤++++++≤+←n n nn n n nn n由夹逼原则可得所求极限为1.解:.11lim 111lim 2222=++++=++++∞→∞→n n n n n n n n n n n n由推论1,.011 (211102)2222→++≤+++++++++≤++←n n nn n n n n n n n n n n由夹逼原则可得所求极限为0. 解:由推论1,21112)1(...221112)1(2122222→++⋅+<+++++++++<++⋅+←n n n n n n n n n n n n n n n n n 由夹逼原则可得所求极限为21.由以上例题可以看出用夹逼原则求极限的关键在于对数列进行恰当的放缩接上去的例题稍有难度,难处仍难在放缩的技巧!2lim n n n ∞→.解:).(42...322212!20放到第二项最大!n n n n ≤⨯⨯⨯⨯=< 且0!4lim =∞→n n .故由夹逼原则可知.0!2lim =∞→n nn解:设),0(1>+=h h α则 从而,)1(202h n nn-<<α因为,0)1(2lim 2=-∞→h n n由夹逼原则可知.0lim=∞→nn nα解:因为,111)!sin(03332323232nn n n n n n n n n ==<+≤+≤(三角函数有界性)即332311)!sin(1n n n n n<+<-,而,01lim 1lim 33==-∞→∞→n n n n由夹逼原则可知.01)!sin(lim 32=+∞→n n n n解:原式.]1)32()31[(3lim ]1)32()31[(3lim 11n n n n n n n n ++=++=∞→∞→ 因为1)32()31(0<+<n n ,31)32()31(1<++<n n ,两边同时乘以n3得到133213+<++<n n n n,再两边同时开n 次方根得到.33]321[311nn n n⨯<++<当∞→n 时,.3lim 3133lim 3)33(lim 11左边右边===⨯=⨯=⨯=∞→∞→∞→n nn nn故由夹逼原则可得.3)321(lim 1=++∞→nn nn解:由取整函数的性质可知[].1x x x ≤≤-当,0时>x [][];即111,1≤≤-≤≤-x x x x x x x x x 当,0时<x [][];即111,1≥≥-≥≥-x x x x x x x x x因为,1)11(lim =-∞→x x 由夹逼原则可得[].1lim =∞→x x x解由取整函数的性质可知)0(1≠≤⎥⎦⎤⎢⎣⎡≤-x x bx b x b ,当0>x 时,各项乘以αx得到ααααbx b x xb≤⎥⎦⎤⎢⎣⎡<-因为,)(lim 0αααbxbx =-+→由夹逼原则可得.lim 0ααbx b x x =⎥⎦⎤⎢⎣⎡+→。
[精品]夹逼定理在人类历史上,夹逼定理一直是一个难题。
从一开始,人类就没有完全解决这个难题。
直到人类有了更好的解决办法,所以夹逼定理才能被我们不断地使用。
现在,我们来学习一下。
我们可以从一开始就给自己定位,明确自己的目标,从而制定相应方向进行努力。
这样做是为了让你在学习的过程中变得更好。
当一个人发现周围出现一种可以用来对付他的敌人时,应该如何采取行动呢?你一定会想找一个办法来对付他。
1.先确定敌人用什么武器。
当我们要向敌人发起进攻时,我们首先会去想这个武器是用来对付敌人的还是自己用来对付敌人的就非常重要了。
比如,你发现一位同学在考试中作弊。
这是你没有采取任何行动的结果。
这时候,这个同学会采取什么办法来报复呢?如果他使用自己的武力来攻击你,那么他也会受到相应的惩罚。
但是如果他使用的是一些其它的武器呢?那他就不会受到惩罚,甚至还会受到更加严重的惩罚。
所以我们必须确定敌人用的是什么武器了?这里有一个方法是:你得先找到一个敌人是谁用的武器或其使用方法最简单、最直接的方法来判断敌我双方都用了哪些武器或方法。
2.用什么武器把他们逼到夹逼定理中的夹逼地方。
假如敌人从一开始就处在夹逼定理的夹逼地,那我们应该如何做呢?首先,我们要先确定一下对手的位置和能力,然后再做相应的准备。
由于对手是在一个不太好的地方攻击他们的,所以我们需要找一个可以对付他的地方,然后从这个地方开始,一步步往上接近他,最后让对手掉到一个更差的地方去威胁他。
接下来我们说一下这个问题究竟有多难:如果敌人不喜欢被攻击,那么这个地方必须是他不喜欢被攻击到的位置上的地方;如果有一个敌人喜欢被攻击,那么这个地方就应该是他不喜欢被攻击到的位置上的地方了。
假如敌人喜欢被攻击到这里了,那么这个地方应该是他不喜欢被攻击到的地方,这就是这个问题给我们带来的一个陷阱。
然后将你找来的东西放在那个地方。
这个东西必须和被攻击的人一模一样才行哦!当我们用别的办法来对付他们时,我们应该做哪里呢?如果大家都已经把这个方法当成一个常规武器了,那就只有一个办法可以让大家这么做了:将你找来最好的武器(也就是最简单的)放在自己需要攻击的地方,然后再找一个最适合这一种情况的武器将他们压到最差位置去。
第六节 夹逼定理 无穷小的比较
一. 夹逼定理
定理1:如果数列{}n x 、{}n y 及{}n z 满足下列条件:
(1)n n n z x y ≤≤,( ,3,2,1=n )。
(2) a y n n =∞→lim ,a z n n =∞
→lim 。
则数列{}n x 的极限存在,且a x n n =∞
→lim 定理2:设函数)(x f 在点a 的的某一去心邻域),(δ∧
a U 内(或X x ≥时)
满足条件:(1))()()(x h x f x g ≤≤。
(2) A x g a x =→)(lim ,A x h a x =→)(lim (或A x g x =∞→)(lim ,A x h x =∞→)(lim )。
则)(lim x f a x →存在,且A x f a x =→)(lim ((或)(lim x f x ∞→存在,且A x f x =∞
→)(lim )。
注:(1)夹逼定理不仅说明了极限存在,而且给出了求极限的方法。
(2) 定理1中的条件(1)改为:n n n z x y ≤≤,( ,3,2,1=n ),结论仍然成立。
例1: 求下列极限
(1)n n n 11lim +∞→ (2))1...2111(lim 222n
n n n n ++++++∞→ 二.两个重要极限
(1)1sin lim 0=→x x x 。
(2)e x x x =+∞→)11(lim ,(e x x x =+→1
0)1(lim ,e n n n =+∞→)11(lim )。
例2:求下列极限
(1) x x x tan lim 0→ (2) 30sin tan lim x x x x -→ (3)203cos cos lim x
x x x -→ 例3:求下列极限
(1) x x x 2)21(lim -∞→ (2) 21
2)2(lim -→x x x (3)x x x x )55(lim -+∞→ 三. 无穷小的比较:在极限的运算法则中,我们讨论了两个基本点无穷小的和、差及乘积仍是无穷小。
那末两个无穷小的商的情况又如何呢?为此讨论下列极限。
尽管,3,1,,,2x Cosx Sinx x x -都是0→x 时的无穷小量,但是它们趋向于零的快慢程度不一样。
设)(x α,)(x β是当0x x →时的两个无穷小量,由极限的运算法则知:)()(x x βα+,)()(x x βα-,)()(x x βα⋅都是当0x x →时的无穷小量。
但)(/)(x x βα当0x x →时是否是无穷小量呢?
,)(x x =α,2)(x x =β,x x sin )(=γ,x x cos 1)(-=δ当0→x 时都是无穷小量,0)()(lim 0=→x x x αβ,1)
()(lim 0=→x x x αγ,21)()(lim 0=→x x x βδ,∞=→)
()(lim 0x x x βα。
1.定义:设0lim =α,0lim =β,
(1)如果0lim =α
β
,就说β是比α高阶的无穷小,记作)(αβo =; (2)如果∞=α
βlim ,就说β是比α低阶的无穷小; (3)如果0lim ≠=c α
β,就说β是与α同阶的无穷小; (4)如果1lim =αβ,就说β与α是等价无穷小,记作βα~。
2.等价无穷小的重要性质
定理3:设/~αα , /
~ββ,且//lim αβ存在,则αβlim =//lim αβ。
推论(1):设/~αα , /
~ββ,且//)()(lim αβx g x f 存在,则αβ)()(lim x g x f 存在,且αβ)()(lim x g x f =//
)()(lim αβx g x f 。
注:在计算极限的过程中,可将分子或分母的的乘积因子换为与其等价的无穷小,这种替换有时可简化计算,但注意在加、减运算中不能用。
例4:求下列极限
(1) x
x x x x tan sin tan lim 20-→ (2) 1tan 1tan 1lim 0---+→x x e x x 例5:当0→x 时,试比较下列无穷小的阶
(1) 232x x +=α 2x =β (2)x x cos 2=α 2x =β
3.常用的等价无穷小替换
0→x :x x ~sin ,x x ~tan ,x x ~arcsin ,x x ~arctan ,x x ~)1ln(+,x e x ~1-;
2
~cos 12
x x -,x x μμ~)1(+。