当前位置：文档之家 › 高数 夹逼准则与两个重要极限.

高数 夹逼准则与两个重要极限.

  • 格式：ppt
  • 大小：544.00 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

高数 夹逼准则与两个重要极限

高数 夹逼准则与两个重要极限
利用两个重要极限判断级数收敛性
对于形如$sum_{n=1}^{infty}frac{sin n}{n}$和$sum_{n=1}^{infty}(1 + frac{1}{n})^{n}$的级数，可以利 用两个重要极限的结论判断其收敛性。
综合应用夹逼准则和两个重要极限
在判断一些复杂级数的收敛性时，可以将夹逼准则和两个重要极限结合起来使用，通过巧妙的放缩和变换， 找到夹逼的级数或函数，从而判断原级数的收敛性。
解答
首先找到与原数列相关的不等式关系， 即∑(ξi1)^2Δxi≤∑f(ξi)Δxi≤∑(ξi)^2Δxi。然 后验证不等式两侧的数列极限是否存 在且相等。对于左侧数列和右侧数列， 当n趋向于无穷大时，其极限均为1/3 （可以通过定积分的几何意义或定积 分计算公式进行验证）。因此根据夹 逼准则，原数列的极限存在且为1/3， 即函数f(x)=x^2在区间[0,1]上的定积 分为1/3。
利用(1+1/x)^x在x→∞时的极限为e，可以对一些涉及指数函数的 复杂表达式进行逼近处理。
在求解某些微分方程时，可以利用这两个重要极限简化方程形 式或求解过程。
在概率论与数理统计中，这两个重要极限也经常出现，例如在 求解某些概率分布或统计量的极限性质时。
THANKS FOR WATCHING
感谢您的观看
02
利用第二个重要极限求解幂函数、指数函数相关问题，如求
(1+x)^(1/x)在x=0处的极限值。
结合洛必达法则等其他求极限方法，可以求解更复杂的极限问
03
题。
拓展：其他常见极限形式及求解方法
∞/∞型极限
通过分子分母同除以某个趋于 无穷的变量来转化为0/0型极 限求解。
1^∞型极限

高数第一章极限存在准则 两个重要极限

高数第一章极限存在准则 两个重要极限

当
时,
当
时,
lim
n
xn

a
令N max N1 , N2,
则n当 N
时, 有
由条件 (1) a yn xn zn a
即xn a ,
l故im
n
xn

a
.
2
例1. 证明
证: 利用夹逼准则 由.
n

n2
1


n2
1
2

n2
1
n


n2
n2
且
lim
n
n
n2 2


lim
n
1
1


n2
1

lim n
n

n2
1


n2
1
2

n2
1
n

1
3
准则1’ 函数极限存在的夹逼准则

当 x (x0 , ) 时, g(x) f (x) h(x) , 且
a
lim
n
xn
b
(m)
b ( 证明略 ) 5
例2. 设
证明数列
极限存在 . (P49)
证: 利用二项式公式(P270 ), 有
xn (1 1n)n

1

n 1!
1 n

n(n1) 2!
1 n2

n(n1)(n2) 3!
1 n3


n(n1)(nn1) n!
1 nn
11
x x0
2

高数1 极限存在准则与两个重要极限

高数1 极限存在准则与两个重要极限

假设 xn xn1 ,
则 x n 1 a x n a x n 1 x n
即 xn单增.
x n 1 从而 1, xn
又 x n a x n 1 ,
2 则 xn a xn1 .
2 a x n 1 a x n a x n 1 1 a 1 xn xn xn a xn xn
即 A g( x) A .
2 0, 当 0 x x0 2时, 有 h( x ) A ,
即 A h( x ) A .
取 min{ 1 , 2 , 0 }. 当 0 x x0 时,
有 A g ( x ) f ( x ) h( x ) A ,
x 2 sin 1 cos x 2 Solution. x x x x 2 sin 2 sin 1 cos x 2 2 2 lim lim lim x x x 2 x 0 x 0 x 0
1 cos x lim x x 0 x x 2 sin 2 sin 2 2 2 lim x x 2 x 0
即 f ( x) A .
lim f ( x ) A.
x x0
x0 ,
x0 ,
x 注意：极限过程为“ x x0 ” (或 x x , x , x 等).
如果数列 xn , yn , zn满足 准则I’： (1) yn xn zn ( n 1, 2,)
1
四. 第二重要极限
1 x lim (1 ) e x x
下面分三步进行讨论.
(1)设x依次按自然数n变化，则函数为 1 n xn f ( n) (1 ) n n 1 n( n 1) 1 n( n 1) ( n n 1) 1 xn 1 2 n 1! n 2! n! n n

1.4 极限存在准则与两个重要极限

1.4 极限存在准则与两个重要极限

( A) e −2; (C ) 0;
2
§1.4 极限存在准则与两个重要极限
思考练习
选择
1 ( 1) lim x sin = ( C ). x →∞ x ( A) ∞; ( B ) 不存在; (C ) 1; ( D ) 0.
（2）lim ( 1 − x ) ）
x →0 − 2 x
=（ D ）
( B ) ∞; ( D) e .
上页 下页 返回
U 准则Ⅰ′ 如果当 x ∈ ( x0 , δ 0 )(或 x > M )时,有 准则Ⅰ′
(1) g ( x ) ≤ f ( x ) ≤ h( x ), ( 2) x→ x g( x ) = A, x→ x h( x ) = A, lim lim
( x→∞ )
0
( x →∞ )
0
存在, 那么 lim f ( x )存在, 且等于 A.
§1.4 极限存在准则与两个重要极限
一、极限存在准则 二、两个重要极限
sin x lim =1 x→0 x
1n lim(1 + ) = e n→∞ n
上页 下页 返回
§1.4 极限存在准则与两个重要极限
一、极限存在准则
1.夹逼准则 1.夹逼准则
准则Ⅰ 满足下列条件: 准则Ⅰ 如果数列 x n , y n 及 z n 满足下列条件:
= e −2 .
上页 下页 返回
§1.4 极限存在准则与两个重要极限
例5
3− x x ) . 求 lim( x →∞ 2 − x
1 x 解 原式 = lim(1 + ) x →∞ 2− x
1 2− x 1 2 ) ⋅ (1 + ) = lim (1 + x →∞ 2− x 2− x

1-4极限存在准则与两个重要极限

1-4极限存在准则与两个重要极限

n 1 所以数列 1 是严格单调增加的； n
n 又由于 1 n 1
1 n 1 n 2

n 1 ( n 1) n 1 1 n , n 2 n 2
( 2) lim f ( x ) A, lim g( x ) A
x x0 x x0

则 lim h( x ) A.
x x0
证
由 f ( x ) h( x ) g( x ), 有
f ( x ) A h( x ) A g( x ) A
所以
h( x ) A max{ f ( x ) A , g( x ) A }
解2
lim x
x 1 x1 lim x x 2 1
x
1 x 2 x
x
1 1 1 1 x x l im lim x x x x 2 2 2 2 1 1 x x e 2 e 1 e
x
3 例8 求 lim x 2
解
x . x
x2 4 1 1 2 x 2
2x
1 原式 lim 1 x 2 x
e2
x1 . 例9 求 lim x x 2
,
n1 1 所以数列 1 是严格单调递降的. n
1 1 于是 1 1 n n
n
n 1
1 1 n 1
2
n
1 1 4 1 n 1 从而数列 1 单调增加, 并且有上界， n n 1 由极限存在准则II， lim 1 存在, 记为e . n n

高等数学 第1章 第七节 极限存在准则 两个重要极限

高等数学 第1章 第七节 极限存在准则 两个重要极限

则
lim
n
x n1
lim n
6 xn ,
A
6 A,
解得 A 3或A 2,（舍去）
lim n
xn
3.
14
3.两个重要极限的应用
例6： 求 lim tan x 1
x0 x
可作为公式
lim
x
s
in u x ux
1
lim ux 0
x
解： lim tan x lim sin x 1 lim sin x lim 1 11 1 x0 x x0 x cos x x0 x x0 cos x
1 n2 1
n2
1
22
n2
1
n2
n n2 1
,
1
lim 1 0, n 2n
lim n n n2 1
lim n
n
1
1
由夹逼定理知：
n2
0 0, 10
lim n
n
1 2
1
n2
1 22
n2
1 n2
存在, 且
lim n
n
1 2
1
n2
1
22
n2
1
n2
0.
8
例2 用夹逼准则证明：
lim sin x 1.
1yn xn zn n 1,2,3,,
2
lim
n
yn
a,
lim
n
z
n
a,
则数列x
n
的
极
限
存
在,
且
lim
n
xn
a.
准则1 若
1当x
U
x

高数上册第一章第六节极限存在准则两个重要极限

高数上册第一章第六节极限存在准则两个重要极限

【几何解释】
单调减少
单调增加
广义单调数列
*
相应地，函数极限也有类似的准则
统称为单调有界准则
准则Ⅱ及
【准则 】
准则
*
【补例2】
【证】 (舍去) 递推公式 注意到
*
【说明】
该方法只有在证明了极限存在时，才能由递推公式，通过解方程的方法求极限，否则可能导致荒谬的结论
如
①式两端取极限后 得
①
从而得
矛盾
*
【例4】
【解】 【例5】 【解】
*
【例6】
【解】 【例7】 【解】
*
三、小结
【两个准则】
【两个重要极限】 夹逼准则; 单调有界准则 .
*
【思考题】
求极限
*
【思考题解答】
抓大头
*
二、两个重要极限
三、小结 思考题
第六节 极限存在准则 两个重要极限
一、极限存在准则
一、极限存在准则
【证】
【夹逼准则】
*
上两式同时成立,
上述数列极限存在的准则可以推广到函数的极限
【注意】
02
利用夹逼准则Ⅰ关键是将xn作适当缩放,得到极限容易求的数列yn与zn，且极限相等.
准则 Ⅰ和准则 Ⅰ'称为夹逼准则.
利用夹逼准则Ⅰ′关键是对不易求极限的f(x)作适当缩放，得到极限容易求的g(x)与h(x)，且极限相等.
*
【补例1】
【解】 由夹逼准则得 抓大头
*
【练习】
［提示］ ［提示］ ［提示］单调有界准则
*
［提示］ ［提示］ 由夹逼定理得 【注】记住[x]的运算性质： 当 x > 0 时
2.【单调有界准则】

高数夹逼准则与两个重要极限

高数夹逼准则与两个重要极限

高数夹逼准则与两个重要极限高数中的夹逼准则和两个重要极限是数学中非常基础而重要的概念。

夹逼准则可以帮助我们求解函数在其中一区间上的极限，而两个重要极限则可以简化我们在计算极限时的计算过程。

下面将详细介绍夹逼准则和两个重要极限。

一、夹逼准则夹逼准则是数学中一种求函数极限的方法。

它适用于其中一区间上的函数。

夹逼准则的基本思想是，如果一个函数在其中一区间内被两个函数夹住，而这两个函数恰好有相同的极限，那么被夹住的函数也会有相同的极限。

具体地说，设函数f(x)在其中一区间[a, b]上有定义。

如果存在两个函数g(x)和h(x)，满足对于所有的x∈(a, b)，有g(x)≤f(x)≤h(x)，并且lim[x→a]g(x) = lim[x→a]h(x) = L，则有lim[x→a]f(x) = L。

夹逼准则的应用非常广泛，特别是可以用来求解一些比较复杂的极限。

1.正无穷大与无穷小之间的比较设函数f(x)在x→a时，当x趋于a时，f(x)的极限为正无穷大∞，即lim[x→a]f(x) = ∞。

那么对于任意的正数M，存在一个正数δ，使得对于所有满足0<，x-a，<δ的x，有f(x)>M，即f(x)比任意的正数M都要大。

同样地，如果函数g(x)在x→a时，当x趋于a时，g(x)的极限为0，即lim[x→a]g(x) = 0。

那么对于任意的正数ε，存在一个正数δ，使得对于所有满足0<，x-a，<δ的x，有，g(x)，<ε，即g(x)比任意的正数ε都要小。

这个极限的意义是，在计算极限时，如果我们发现函数f(x)在x→a时可以无限增大而无限接近正无穷大，那么我们可以将它近似地看作一个无穷大，这样可以简化计算过程。

同样地，如果函数g(x)在x→a时可以无限接近0，那么我们可以将它近似地看作一个无穷小。

2.正无穷大与负无穷大之间的关系如果两个函数f(x)和g(x)满足lim[x→a]f(x) = +∞，lim[x→a]g(x) = -∞，那么它们之间的关系为：当x→a时，f(x)比g(x)大无穷小。

极限存在准则与两个重要极限资料

极限存在准则与两个重要极限资料

1
(1
1 )(1
2 )(1
n1 )
2! n
n! n n
n
xn

11
1 2!
1 n!

11
1 2

1 2n1

3

1 2n1

3,
{xn}是有界的; 单调上升有上界必有极限
lim n
xn
存在.
记为 lim(1 1)n e
n
n
(e 2.718281828459045) 无理数
12 23
n1 n
2 1 2, n
{ xn}是有上界的;
因此, 利用单调有界数列必收敛准则即得结论.
15
2.5 极限存在准则 两个重要极限
例 证明数列 xn 3 3 3
(n重根式)的极限存在.
证 (1) 显然 xn1 xn ,
{xn}是单调增加的; (2) x1 3 3, 假定 xk 3,
1.
8
2.5 极限存在准则 两个重要极限
0
例 lim x 0 lim
x
lim sin x 1 lim x 1
x0 x
x0 sin x
cos x 1.
x0 tan x x0 sin x
例
sin3 3 lim x0 3x
x
0
0
1 3
lxim0
sin
3
3
x
x
3
n
an

bn

cn ,求 lim n
xn .
解 法一 由于 a xn a n 3
1
以及 lima a, lim a n 3 lim a 3n a 1

极限存在准则与两个重要极限

极限存在准则与两个重要极限

100 000 2.718 27 100 000 2.718 30
1 000 000 2.718 28 1 000 000 2.718 28
e e
1.2 准则Ⅱ与第二个重要极限
因此，
lim
x
1
1 x
x
e
．
e 是无理数，它的值是 2.718 28 ．在 1.1 中提到的指数函数 y ex 及自然对数 y ln x 中的
（2） lim g(x) lim h(x) A ，
xx0
xx0
则有 lim f (x) A ． xx0
1.1 准则Ⅰ与第一个重要极限
作为准则Ⅰ及准则Ⅰ'的应用，下面证明一个重要极限： lim sin x 1 ． x0 x
证明 在图所示的单位圆中，设圆心角 BOA x ， AD 切圆 O 于 A ， 且与 OB 延长线相交于 D ，于是有
3 1
x 1
1
lim
x 1
3
x
2x 1
2x
lim
x
2x 2x
3 1
lim
x
1 1
3
x
2x
1 x 2x
1
3
e2
1
e2
e．
1.7 无穷小阶的比较
在 1.4 节中我们已经知道，两个无穷小的和、差及乘积仍是无穷小．但是关于两
个无穷小的商却会出现不同的情况．例如，当 x 0 时，2x ， x2 ，sin x 都是无穷小
an1
1
n
1
n1
1
1
1
21!1
n
1
1
1 3!
1
1 n
1

两个极限存在准则和两个重要的极限

两个极限存在准则和两个重要的极限

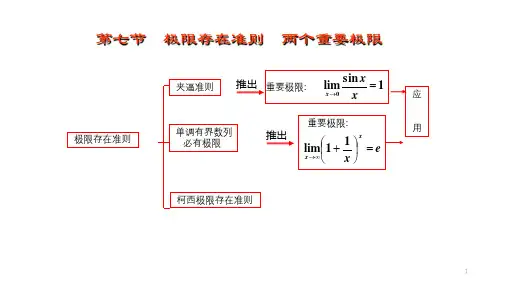
两个极限存在准则和两个重要的极限1.两个极限存在准则(1) 夹逼准则：设a, b, c为实数，如果函数f(x)在a的一些左邻域内对于一切x都有h(x)≤f(x)≤g(x)，且lim[x→a]h(x)=lim[x→a]g(x)=L，则必有lim[x→a]f(x)=L。

夹逼准则的本质是通过构造两个函数作为边界来确定原函数的极限。

(2) 单调有界准则：设函数f(x)在(a, b)上单调递增(递减)，且在(a, b)上有界，则必有lim[x→a]f(x)=sup{f(x)}(或lim[x→a]f(x)=inf{f(x)})。

单调有界准则的基本思想是通过函数的单调性和有界性来确定极限。

(1) 无穷小极限：设函数f(x)在x=a处有极限lim[x→a]f(x)=0，如果对于任意正数ε，存在对应的正数δ，使得对于所有满足0<，x-a，< δ的x，有，f(x)，<ε，那么称函数f(x)在x=a处的极限为0。

无穷小极限的重要性在于它在微积分中有广泛应用。

例如，微分定义中的导数可以看作是函数在其中一点的极限，这也符合函数在该点的变化趋势比较明显。

无穷小极限的概念使得我们能够更好地描述和理解函数在其中一点的变化情况。

(2) 无穷大极限：设函数f(x)在x=a处有极限lim[x→a]f(x)=∞，如果对于任意正数M，存在对应的正数δ，使得对于所有满足0<，x-a，< δ的x，有f(x) > M，那么称函数f(x)在x=a处的极限为无穷大。

无穷大极限的重要性在于它可以帮助我们研究函数在其中一点的增长速度和趋势。

例如，在极限定义中，我们可以通过无穷大极限来刻画函数在其中一点的无限增长或无限逼近的情况。

此外，无穷大极限也在微积分中的积分定义中有重要的应用，帮助我们理解函数的积分和面积的概念。

综上所述，极限的存在准则和重要的极限是微积分中的重要概念。

了解它们的定义和应用可以帮助我们更好地理解和分析函数在其中一点的变化情况，为进一步研究微积分和数学分析打下坚实的基础。

高等数学教案 1.4 两个重要极限

高等数学教案 1.4 两个重要极限

§1.4 两条极限存在准则 两个重要极限【教学内容】：1、夹逼准则2、单调有界准则3、两个重要极限【教学目的】：1、了解函数和数列的极限存在准则2、会用两个重要极限求极限【教学重点】：应用两个重要极限求极限【教学难点】：应用函数和数列的极限存在准则证明极限存在，并求极限。

【教学设计】：首先通过几个具体的数列的求极限例子：从有限到无穷，从已知到未知，引入新知识。

介绍两条极限存在准则（夹逼准则，单调有界准则）及其利用他们求数列函数的极限（50分钟）。

再介绍两个重要极限及x xxx (1sin lim 0=→为弧度）的证明（20分钟），讲解例题（20分钟），课堂练习（10分钟）。

【教学内容】：引入：考虑下面几个数列的极限1、∑=∞→+1000121limi n i n 1000个0相加，极限等于0。

2、∑=∞→+ni n in 121lim 无穷多个“0”相加，极限不能确定。

3、n n x ∞→lim ，其中12-+=n n x x ，21=x ，极限不能确定。

对于2、3就需要用新知识来解决 一、夹逼准则夹逼准则：当),(0δx U x o∈时，有)()()(x h x g x f ≤≤，且A x f x x =→)(lim 0=)(lim 0x h x x →，则A x g x x =→)(lim 0。

推论：设}{n x 、}{n y 、}{n z 都是数列，且满足n n n z y x ≤≤，又=∞→n n x lim A z n n =∞→lim ，则有A y n n =∞→lim 。

例1、 求∑=∞→+ni n in 121lim 。

解：因为=+12n n 111111222++++++n n n ≤++++++≤n n n n 22212111nn nn nn ++++++222111 nn n +=2而=++∞→1lim2n nn 1lim 2=++∞→nn nn所以∑=∞→+ni n in 121lim =1注意：夹逼准则应恰当结合“放缩法”使用 二、单调有界准则单调有界数列必有极限（1）单调上升有上界的数列，极限一定存在； （2）单调下降有下界的数列，极限一定存在。

夹逼准则与两个重要极限

夹逼准则与两个重要极限

第二个重要极限的应用举例
在解决一些数学问题时，如求无穷积分、求解微分方程等，可以利用第二 个重要极限来简化计算过程。
例如，在求解无穷积分∫sin(x)/x dx时，可以利用第二个重要极限来得到 积分的值。
此外，在求解一些微分方程时，也可以利用第二个重要极限来得到方程的 解。
05
总结与展望
本主题的主要内容总结
夹逼准则的定义与性质
夹逼准则是数学分析中的一个基本定理，它描述了当两个序列或函数在一定条件下收敛时，它们的极限值之间的关系 。这个定理在证明极限和求极限中有着广泛的应用。
两个重要极限的介绍
两个重要极限是数学分析中的重要概念，它们是用来描述函数在某些特定点或区域的极限行为。第一个重要极限是 $lim_{x to 0} frac{sin x}{x} = 1$，第二个重要极限是$lim_{x to infty} frac{1}{x} = 0$。
03
数，如泊松分布的均值和方差。
04
第二个重要极限
第二个重要极限的定义
01
02
03
第二个重要极限是数学 中的一个重要概念，它 描述了当x趋向于无穷大 时，函数sin(x)/x的极限
值。
具体来说，第二个重要极 限的定义为lim(x->∞) sin(x)/x = 1。
这个极限在解决一些数 学问题时非常有用，尤 其是在处理无穷大或无
夹逼准则的应用举例
举例1
求lim (1 + 1/n)^n (n -> +∞) 的值。令c_n = (1 + 1/n)^n， a_n = (1 + 1/n)^(n+1)，b_n = (1 + 1/n)^(n-1)，则有a_n <= c_n <= b_n。根据夹逼准则，lim c_n = e。

高等数学 第二章 极限与连续 2.6 两个重要极限

高等数学 第二章 极限与连续 2.6 两个重要极限
sin kx kx k lim sin kx kx
k 1 k .
解： 原式 k lim x 0
kx 0
例4
求
2 sin x
2 2 x 2
解： 原式 lim 例5 求
x 0
sin lim x 2 x 0 2
1
x 2

2

1 2
1
2
解： 令 t
例11
求 x
lim (
x 2
x
2
2
x 1
)
x
x x x x 解： lim ( 2 ) lim lim x x x x 1 x 1 x 1 x 1 x 1
x
x
x
x
1 1 lim 1 1 x x 1 x 1
x,
OAB 的高为 BD ,
于是有
sin x BD ,
tan x AC ,
C
二、两个重要极限
B
(1)
lim
sin x x
x 0
1
0 0
型
x
o
D
A
△AOB 的面积＜圆扇形AOB的面积＜△AOD的面积
即
1 2
sin x

1 2
tan x
(0 x

2

2
sin x x tan x ,
单调减少
定理2.12
准则Ⅱ
单调有界数列必有极限.
几何解释:
m
x1
x 2 x 3x n x n 1
A
M
x
C

高数 极限存在准则两个重要极限

高数 极限存在准则两个重要极限

2x lim[(1 ) x 0 1 x
1 x 2 cos x x 2x 1 x sin x
]
e
2
14
例11 lim 3 x 9
x
1 x x
1 x

lim 9
x
1 x x

1 x 1 3
3x
1 9 lim 1 x x 3
2
).
解
n n2 n

1 n2 1

1
1 n2 n

n n2 1
n 又 lim 2 lim n n n n
1 1, 1 n n 1 lim 2 lim 1, 由夹逼定理得 n n 1 n 1 1 2 n
lim(
n
1 n 1
17
11
例6. 求 解: 令 t arcsin x , 则 x sin t , 因此
t 原式 lim t 0 sin t
例7. 求
解: 原式 =
x 2 sin 2 2 lim 2 x0
sin t t
1
x
sin 1 lim x 2 x 0 2
x 2
1 2 2 1
2

1 n 2
2

1 n n
2
) 1.
4
记住结果：
(1) lim n n 1
n
n
( 2) lim n a 1 ( a 0)
例2
lim 1 2 3 4
n n n n
n
解： 4 n 1 2 n 3n 4 n 4n 4

极限存在法则 两重要极限

极限存在法则 两重要极限
1 1 1 又注意到: 又注意到: xn < 1 + 1 + + + ⋅ ⋅ ⋅ + 2! 3! n!
高等数学（ 高等数学（上）
1 [ x] 1 x 1 [ x]+1 (1 + ) ≤ (1 + ) ≤ (1 + ) , [ x] + 1 x [ x] 1 [ x]+1 1 [ x] 1 而 lim (1 + ) = lim (1 + ) ⋅ lim (1 + ) x→+∞ x→+∞ x→+∞ [ x] [ x] [ x] =
高等数学（ 高等数学（上）
例 2 证明 lim
n→∞
n
n
n =1
n(n − 1) 2 n(n − 1) 2 n xn + ... + xn > xn ⇒ n = (1 + xn ) = 1 + nxn + 2 2 2 2 2 2 lim = 0. ; n→∞ ⇒ xn < ⇒ 0 < xn < n −1 n−1 n−1 由夹逼准则⇒lim xn = 0 ⇒ lim n n = 1.
数列{xn}
单调增加 ,若 x1 ≤ x2 ≤ ⋅ ⋅ ⋅ ≤ xn ≤ ⋅ ⋅ ⋅ 单调减少 ,若 x1 ≥ x2 ≥ ⋅ ⋅ ⋅ ≥ xn ≥ ⋅ ⋅ ⋅
准则Ⅱ(单调有界收敛准则)单调有界数列必有极限. 准则Ⅱ(单调有界收敛准则)单调有界数列必有极限. Ⅱ(单调有界收敛准则 几何解释: 几何解释:
第六节
极限存在准则
两个重要极限
夹逼准则) 准则 I (夹逼准则) 如果{ x n }， y n } 及 { z n } { 满足下列条件： 满足下列条件： （1） yn ≤ xn ≤ zn （2） lim yn = a
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
则有 f(x) A (xx0或x)
( 例1 求 lim n
1 n2 1
n
n

1
1 n2 2
2

1
1 n2 n
2
).
n n2 1
解 因为 又
n n
2
n 1
lim
n

1 1 1 n 1
n n
1

lim
n
n n
2
lim
n
n n2 1
第五节
夹逼准则与两个重要极限
利用极限的定义及运算法则虽可以求得很多函数的 极限，但是对于一些特殊函数的极限却无能为力，如
tan x lim , x 0 x
3 x 2x lim( ) x 2 x
极限值各是多少？如何求解？ 一、夹逼准则 二、两个重要极限
一、夹逼准则
准则I 如果数列{xn}, {yn}, {zn}满足 (1) yn xn zn, (n =1,2,3…)；
解
x 2 sin 1 cos x 2 lim lim 2 2 x 0 x 0 x x
2
2
sin x 1 时，有三处必须一致，公式的 在使用公式 lim x 0 x sin ( x) 一般形式为
( x ) 0
x sin 1 1 2 1 2 lim 1 . 2 x 0 x 2 2 2 例3—例7可以作为公式使用. 通过这些例子可以看到，
2.71827 2.71828
-0.000001 2.71828
从表中可以看出，当 t 0 时，
(1 t ) 2.71828
可以证明这个极限是无理数，将其记作e， e 2.71828 .这样就有
1 t
lim(1 t ) e
t 0
1 t
或
1 x lim(1 ) e x x
1
lim
n
由夹逼准则得
lim(
n
1 1 2 n

1
1 n 2
2
1 n n
2
n 1
2
) 1.
sin x si n0 0 li m ? x 0 x 0 0
二、两个重要极限
sin( x ) sin x 证 因为 , 故只讨论x0+的情形. x x 如图, 在单位圆中,AOB = x, BD = sinx, AC=tanx,
sin x (1) lim 1. x 0 x
SAOB < S扇形AOB < SAOC , 1 1 1 sin x x tan x , 所以 2 2 2 x 1 1 , cos x sin x 1, sin x cos x x sin x 由夹逼准则, 得 lim 1. x 0 x
.
lim
( x)
1
1 例8. 求 lim x sin x x
解: 原式
1
例9.
求
解: 原式
3 2
1 （2） lim 1 e. x x 1 ( 1 ) 1, 这是一个非常重要的极限.当 x 时，底数 x
指数 x ，称为 1

x
t 0 ，可以得到此极限的另一个等价形式
1 型极限.若令 x t ，则 x 时，
1 t
lim(1 t 从函数的图形中可以看出
3
y (1 t )
1 t
此极限存在。
. t
我们在 t 0 左右两侧附近计算出一些点的对应函数值 列表观察函数极限值。 t<0 t>0
因为
例3
求
sin kx sin k x lim k 解 lim x0 x x 0 kx sin k x k k lim x 0 k x
tan x . 例4 求 lim x 0 x tan x sin x 1 lim 11 1. 解 lim x 0 x 0 x x cos x
1 例11 求 lim1 . x x
解
x
1 1 lim 1 lim 1 x x x x
bx
x
x 1
1 e . e
1
a 例12 求 lim1 . x x
例5. 求
解: 令 t arcsin x , 则 x sin t , 因此
t 原式 lim t 0 sin t
例6. 求
sin t t
1
解: 令 t arctan x , 则 x tan t , 因此 t 原式 lim 1 tan t t 0 tan t
t
1 cos x . 例7 求 lim 2 x 0 x
x
x 11
2 lim1 x x 1
2 lim1 x x 1
e 2 1 e 2
x 1
2 lim1 x x 1
2 lim1 x x 1
-0.5 -0.1 4.00000 2.86797 0.5 0.1 2.25000 2.25374
-0.01
-0.001
2.73200
2.71964
0.01
0.001
2.70481
2.71692
-0.0001
-0.00001
2.71842
2.71830
0.0001
0.00001 0.000001
2.71815
(2) lim yn a, lim z n a,
n n
xn a. 则数列{xn}的极限存在, 且 lim n
o
准则I
如果当
x U x0 , (或| x| > M)时, 有
（ 1） g(x) f(x ) h(x)
(2) g (x) A, h(x) A (xx0或x),
解
a a lim1 lim1 x x x x
bx
x ab a
e .
ab
x 1 例13 求 lim . x x 1
解
x
2 x 1 lim lim1 x x 1 x x 1