具有简单级数的反应
- 格式:doc
- 大小:35.50 KB
- 文档页数:2

简单级数反应的速率方程(1)一级反应动力学凡是反应速率与作用物浓度一次方成正比的反应为一级反应。
放射性元素的蜕变是典型的一级反应,如镭蜕变为氡和氦:Ra 22688→Rn 22286+He 42五氧化二氮的分解反应也是一级反应:N 2O 5→N 2O 4+21O 2 (1) 动力学方程 对于反应A → P ,速率方程为r = k [A] td d[A]-= k [A] 分离变量、积分,并利用初始条件:当t =0时,反应物A 的浓度为[A]0浓度与时间的关系为t k =[A][A]ln 0 )ex p([A]A][0t k -= 如果令[A]0= a ,至t 时刻反应物消耗的浓度为x ,那么转化率 y = x / a ,反应物剩余的浓度为a-x ,则上面的结果可以写成t k x a a =-ln 或 t k y =-11ln以上各式均为速率方程的积分式,都是一级反应的动力学方程。
对于气相一级反应,只要将浓度[A]用压力p A 替代,处理方法及动力学规律完全相同。
(2) 动力学特征① 线性关系 ln{[A]} 对t 作图应为一直线,其斜率等于 - k 。
这一特点在处理一级反应实验数据时尤其重要。
② 速率系数k 的量纲[时间]-1③ 半衰期 [A] = 2A][0或21==a x y (即反应物消耗了一半)所需的时间称为半衰期(half-life)21t一级反应的半衰期 kk t 693.02ln 21==可见,一级反应的半衰期与反应的速率系数k 成反比,而与反应物的起始浓度无关。
. 二级反应动力学(1) (单纯)二级反应动力学 对于反应2A → P ,速率方程为r = k 2 [A]2。
浓度对时间的微分方程: dt d[A]-= k [A]2(其中k=2k 2 ) 浓度与时间的关系为t k =-0A][1[A]1同样令[A]0= a ,至t 时刻反应物消耗的浓度为x (转化率 y = x / a ),反应物剩余的浓度为a -x ,则上面的结果可以写成 t k a x a =--11 或 t k y a y =-)1(对于气相反应,反应速率方程为 2A p k r p p '=,相应的微分方程为tp d d A -= k p 2A p (其中 k p =2p k ' ) 动力学方程为t k p p p =-0A,A 11 (单纯)二级反应动力学有如下两个特点:二级反应有如下一些特征:(1)二级反应速率与作用物浓度的二次方成正比,其速率常数单位为时间单位和浓度单位乘积的倒数;(2)二级反应的作用物浓度的倒数与时间成直线关系,直线的斜率为2k ;(3)二级反应的半衰期为速率常数和作用物初始浓度乘积的倒数。
![具有简单级数的反应[整理版]](https://uimg.taocdn.com/d1dc7073ae1ffc4ffe4733687e21af45b307fead.webp)
具有简单级数的反应化学反应中,表示反应速率与浓度之间的参数的关系,或表示浓度等参数与时间关系的方程称为化学反应的速率方程,也称为动力学方程。
在化学反应的速率方程中,各物浓度相的指数之代数和就称为该反应的级数。
在这些反应中存在具有简单级数的反应,以下就讨论这些具有简单级数的反应,介绍其速率方程式的微分式、积分式以及他们的速率常数k 的单位和半衰期等各自的特征。
一级反应:凡是反应速率只与物质浓度的一次方呈正比关系者称为一级反应。
设有以下一级反应 t=0 C A (0)=a C P (0)=0t=t C A =a-x C P =x 反应速率方程微分式有对其作不定积分得 ln(a-x)=-k 1t+C对其作定积分有 ln[a/(a-x)]= k 1tk 1=1/t ln[a/(a-x)]从反应物起始浓度a 和t 时刻的浓度a-x 即可算出速率常数k 1,一级反应的速率常数单位为1/(时间)。
取反应物消耗了一半所需时间作半衰期,则t 1/2=ln2/ k 1一级反应的特征有3点:1.速率常数的单位是时间的倒数;2.一级反应半衰期与反应物起始浓度无关;3.lnC A 与t 呈线性关系。
二级反应:反应速率和物质浓度的二次方成正比者称为二级反应。
通式为(1)A+B P+…… r= k 2[A][B](2)2A P+…… r= k 2[A] ²若A 和B 起始浓度相同,反应(1)的速率方程可写成dx/dt=k 2(a-x) ²移项作不定积分得: 1/(a-x)= k 2t+C作定积分得: 1/(a-x)-1/a= k 2tk 2=1/t*x/[a(a-x)]其半衰期为 t 1/2=1/k 2a二级反应的半衰期与一级反应不同,它与反应物的起始浓度成反比。
二级反应的特点:1.速率常数的单位是1/[(浓度)(时间)];2.半衰期与反应物的起始浓度成反比;3.1/(a-x)与t 呈线性关系。
若A 和B 起始浓度不相同则反应(1)的速率方程为dx/dt=k 2(a-x)(b-x)a 和b 分别为A 、B 起始浓度,x 为t 时刻已反应物质的量。


简单级数反应的特点总结一、简单级数反应的动力学方程对于单向反应aA→P,若以[A]o,x,y分别表示反应物A的起始浓度,已反应的部分浓度及已反应的百分数,则其t 时刻的剩余浓度[A]应为:[A]=[A]o-ax=[A]o(1-y)而(一)一级反应反应速率与物种浓度成正比的反应为一级反应,其速率方程为:分离变量,积分,则得一级反应的动力学方程:或根据上述各式,可以看出一级反应具有下列特征:(1)若以ln{A] 对t作图,可得一斜率为(-ak),截距为ln[A]o的直线。
(2)若化学计量系数a=1,则可见,上式浓度项是以比值的形式出现的,因此任何与浓度成比例的物理量均可代替之而无须监测真实的浓度,且不影响k的值。
其量纲为(时间)-1,可用s-1,min-1或h-1等表示之。
(3)若y=1/2 ,即反应物浓度[A]降低到其初始值的一半所需时间称为"半衰期",以t1/2表示,则有表明半衰期与反应物的起始浓度无关。
(4)若定义反应物A的平均寿命为该反应物由开始反应到通过反应而消耗完全的平均经历时间,则其平均寿命为可见,若a=1,则一级反应的平均寿命的倒数即为其反应速率常数。
又由式容易看出,当=(ak)-1时,[A]=[A]o/e ,即反应物浓度下降到其起始值的1/e 。
这一关系提供了测量一级反应平均寿命的方法。
(二)二级反应二级反应有纯二级和混二级两种类型。
如果反应的计量方程为aA+bB+…→P+…则二种速率表示式分别为类型Ⅰ-d[A]/adt=k[A]2类型Ⅱ-d[A]/adt=k[A][B]先讨论类型Ⅰ。
对式移项,积分可得:由之可得纯二级反应具有如下特征:(1)若以1/[A] 对t 作图,可得一斜率为ak 的直线。
(2)若在不同的反应时间t1,t2,…t n测得反应物A的浓度是[A]1,[A]2,…[A]n,则([A]o-[A]1)/at1[A]o[A]1=([A]o-[A]2)/at2[A]o[A]2=…=([A]o-[A]n)/at n[A]o[A]n=k=常数(3)速率常数k的量纲为浓度-1·时间-1,常用单位为mol-1·dm3·s-1。






动力学思考题1、判断下列说法是否正确(1)反应级数等于反应分子数(2)反应级数不一定是简单的正整数(3)具有简单级数的反应是基元反应(4)不同反应若具有相同级数形式,一定具有相同反应机理(5)反应分子数只能是正整数,一般不会大于三(6)某化学反应式为A+B=C,则该反应为双分子反应2、阿累尼乌斯经验式的适用条件是什么?实验活化能Ea对基元反应和复杂反应有何不同?3、平行反应AE1>E2,若B是所需的产品,从动力学角度定性的考虑应采用怎样的反应温度?4、对1—1级的平行反应,若要改变两产物的浓度[B]、[C]的比,采用改变反应时间的办法行否?为什么?5、平行反应的速控步骤是快步骤;连串反应的速控步骤是慢步骤。
对吗?6、阀能的物理意义是什么?它与阿累尼乌斯经验活化能在数值上的关系如何?7、为什么在简单碰撞理论中,要引入概率因子P?8、一反应在一定条件下的平衡转化率为20%,当加入某催化剂后,保持其它反应条件不变,反应速率增加了10倍,问平衡转化率将是多少?9、某反应反应物反应掉5/9所需的时间是它反应掉1/3所需时间的2倍,该反应是几级反应?10、半衰期为10天的某放射形元素8克,40天后其净重为多少克?11、某反应速率常数的量纲是[浓度]-1[时间]-1,则该反应是几级反应?12、催化剂能极大的改变反应速率,以下说法错误的是(A)催化剂改变了反应历程(B)催化剂降低了反应历程(C)催化剂改变了反应平衡,使转化率提高了(D)催化剂同时加快了正向与逆向反应13、在一连串反应A→B→C中,如果需要的是中间产物B,为得其最高产率应当采用哪种做法?14、温度对反应速率的影响很大,温度变化主要是改变下列哪一项?(1)活化能;(2)反应机理,(3)物质浓度或分压;(4)速率常数;(5)指前因子动力学思考题答案1、判断下列说法是否正确(1)反应级数等于反应分子数(2)反应级数不一定是简单的正整数(3)具有简单级数的反应是基元反应(4)不同反应若具有相同级数形式,一定具有相同反应机理(5)反应分子数只能是正整数,一般不会大于三(6)某化学反应式为A+B=C,则该反应为双分子反应答:(1),(3),(4),(6)错;(2),(5)对2、阿累尼乌斯经验式的适用条件是什么?实验活化能Ea对基元反应和复杂反应有何不同?答:适用于温度区间不大的基元反应和具有明确反应级数和速率常数的复杂反应。
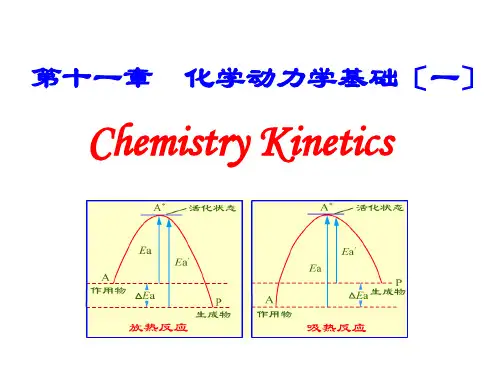
第六章化学动力学6.1 化学反应速率方程6.1-1 化学反应速率表示法6.1-2 化学反应的速率方程①基元反应和总(包)反应②反应级数和反应速率常数6.2 具有简单级数反应的速率公式6.2-1 一级反应6.2-2 二级反应6.2-3 三级反应6.2-4 零级反应6.2-5 反应级数的测定6.3 几种典型的复杂反应6.3-1 对峙反应(可逆反应)6.3-2 平行反应6.3-3 连续反应6.3-4 稳态假定和决速步骤6.4 反应速率与温度的关系6.4-1 Arrenius公式6.4-2 活化能的概念及从实验求活化能6.5 基元反应速率理论6.5-1 碰撞理论6.5-2 过渡态理论6.6 溶液中的反应6.6-1 扩散控制反应6.6-2 溶剂对反应速率的影响6.6-3 离子强度的影响6.7 催化反应6.7-1 催化作用及其特征6.7-2 酸碱催化6.8 光化学6.8-1 光化学基本定律6.8-2 光合作用6.8-3 空气的光化学定义:研究化学反应速率的学科基本任务:1)研究浓度、温度、介质和催化剂等反应条件对反应速率的影响2)阐明化学反应的机理和研究物质结构和它们反应性能之间的关系6.1化学反应速率方程6.1-1化学反应速率表示法常以反应物或产物浓度随时间变化率来表示。
由于在一般的反应式中反应物与生成物的计量系数常不相同,故[reagent][resultant]d ddt dt≠于是引入:反应进度ξ对于aA bB gG hH +→+反应速率11111G A B Hdc dc dc dc d r V dt a dt b dt g dt h dtξ==−=−==V:反应系统的体积r:整个反应速率量纲:浓度.时间-1(mol.dm -3.s -1)反应速率的实验测定:通过测定反应物(生成物)浓度随时间变化z 化学法:化学分析方法测定浓度,采取骤冷、稀释、移去催化剂,加入阻化剂等使反应停止或减慢特点:直接,但费时较多,操作不便z 物理法:物理性质随时间变化来衡量速率(压力、体积、颜色、电导等)特点:迅速,不必中断反应,非直接,找出浓度变化⇔物理性质6.1-2化学反应的速率方程z 在一定温度下,表示反应速率与浓度的函数关系(微分形式)或表示浓度与时间关系的方程(积分形式)成为化学反应的速率方程(动力学方程)。
第二节 具有简单级数的化学反应
一、零级反应
对于反应 →A 产物
化学反应速率与反应物浓度的零次方成正比的反应称为零级反应 A 0A A A k c k dt
dc ==-
与浓度无关 ⎰⎰-=t 0c c A
dt dc A 0,A 得t k c c A 0,A A -= 特征:
1)速率常数的单位:浓度.时间-1
2)A c 与t 呈直线关系
3)半衰期A
0.A 212k c t =
与反应物初始浓度成正比。
二、一级反应
1.化学反应速率与反应物浓度的一次方成正比的反应称为一级反应。
如:
A A A dc v kc dt
=-= 或 A
A
dc kdt c =- 积分,00A A c t
A A c dc k dt
dt -=⎰⎰ 得:,0
ln A A A c k t c = 或,01ln A A A
c t k c = 如果用χA 表示t 时刻反应物A 的转化率,则
,0,0A A A A c c c χ-=
2.一级反应的特征 ① ㏑{ c A /[c ] }与t /[t]作图成为直线关系。
直线的斜率-k ,
② 一级反应速率常数k 的单位,[k]=[时间]-1,。
§10.2 具有简单级数的反应一、一级反应(first order reaction )定义:反应速率只与反应物浓度的一次方成正比的反应称为一级反应。
注:常见的一级反应有放射性元素的蜕变、分子重排、五氧化二氮的分解等。
例: 设有某一级反应: 速率方程的微分式为:或不定积分式: 定积分式: 或 ( ) 半衰期: 即:一级反应的半衰期与反应物起始浓度无关,是一个常数。
注:一级反应的特点1. 速率常数 k 的单位为时间的负一次方,时间 t 可以是秒(s),分(min),小时(h),天(d)和年(a)等。
2. 半衰期是一个与反应物起始浓度无关的常数。
3. 与时间 t 呈线性关系。
见教材P165例题1二、二级反应 (second order reaction)定义:反应速率方程中,浓度项的指数和等于2 的反应称为二级反应。
常见的二级反应有乙烯、丙烯的二聚作用,乙酸乙酯的皂化,碘化氢和甲醛的热分解反应等。
例如,有基元反应:对于22622242268886288Ra Ra He [Ra]r k −−→+=25242251N O N O O [N O ]2r k −−→+= A P−−−→A,0 0 0t c a==A t t c a x x==-A P 1A d d d d c c r k c t t=-==1d ()d x r k a x t ==-1ln()a x k t -=-+常数1ln a k t a x =-11ln 1k t y =- x y a =令:1/21ln2 t k =)ln(x a -2(1) A B P [A][B]r k +−−→+=22(2) 2A P [A]r k −−→+=2(1) A B Pk +−−→0 0 t a b = t t a -x b -x x =2d ()() d x k a x b x t =-- a b =(1) 当时22d ()d x k a x t =-2 1k t a x=+-常数不定积分式:定积分式: 或 ( ) 半衰期:注:二级反应(a=b )的特点1. 速率常数 k 的单位为[浓度] -1 [时间] -1 ;2. 半衰期与起始物浓度成反比 ;3. 与 t 成线性关系。
具有简单级数的反应
化学反应中,表示反应速率与浓度之间的参数的关系,或表示浓度等参数与时间关系的方程称为化学反应的速率方程,也称为动力学方程。
在化学反应的速率方程中,各物浓度相的指数之代数和就称为该反应的级数。
在这些反应中存在具有简单级数的反应,以下就讨论这些具有简单级数的反应,介绍其速率方程式的微分式、积分式以及他们的速率常数k 的单位和半衰期等各自的特征。
一级反应:凡是反应速率只与物质浓度的一次方呈正比关系者称为一级反应。
设有以下一级反应
t=0 C A (0)=a C P (0)=0
t=t C A =a-x C P =x
反应速率方程微分式有
对其作不定积分得 ln(a-x)=-k 1t+C
对其作定积分有 ln[a/(a-x)]= k 1t
k 1=1/t ln[a/(a-x)]
从反应物起始浓度a 和t 时刻的浓度a-x 即可算出速率常数k 1,一级反应的速率常数单位为1/(时间)。
取反应物消耗了一半所需时间作半衰期,则
t 1/2=ln2/ k 1
一级反应的特征有3点:1.速率常数的单位是时间的倒数;2.一级反应半衰期与反应物起始浓度无关;3.lnC A 与t 呈线性关系。
二级反应:反应速率和物质浓度的二次方成正比者称为二级反应。
通式为 (1)A+B P+…… r= k 2[A][B]
(2)2A P+…… r= k 2[A] ²
若A 和B 起始浓度相同,反应(1)的速率方程可写成
dx/dt=k 2(a-x) ²
移项作不定积分得: 1/(a-x)= k 2t+C
作定积分得: 1/(a-x)-1/a= k 2t
k 2=1/t*x/[a(a-x)]
其半衰期为 t 1/2=1/k 2a
二级反应的半衰期与一级反应不同,它与反应物的起始浓度成反比。
二级反应的特点:1.速率常数的单位是1/[(浓度)(时间)];2.半衰期与反应物的起始浓度成反比;3.1/(a-x)与t 呈线性关系。
若A 和B 起始浓度不相同则反应(1)的速率方程为
dx/dt=k 2(a-x)(b-x)
a 和
b 分别为A 、B 起始浓度,x 为t 时刻已反应物质的量。
作不定积分得: 1/(a-b)ln[(a-x)/(b-x)]= k 2t+C
作定积分得: k 2=1/[t(a-b)]ln{[b(a-x)]/[a(b-x)]}
因为a ≠b ,半衰期对A 和对B 而言是不一样的。
dx
(a-x) =k 1dt
A k1 P
对于反应(2),其速率方程为:dx/dt=k2(a-2x)²
定积分得1/(a-2x)-1/a=2k2t
另外,在气相反应中,有k p=k c(RT)^(1-n)
反应速率与物质浓度的三次方成正比者称为三级反应。
其特征为:1.速率常数单位为1/(浓度)²(时间);2.半衰期t1/2=3/2(1/k3a²);3.1/[(a-x) ²]与t呈线性关系。
三级反应为数不多,在气相反应中目前仅知有5个反应属于三级反应。
反应速率与物质的浓度无关者称为零级反应,其速率可表示为:r=dx/dt=k0
移项积分得:x=k0t t1/2=a/2k0
总级数为零级的反应并不多,已知的零级反应中最多的是表面催化反应。
设某反应速率方程为r=k (C A^α)(C B^β)
该反应反应级数显然是(α+β),若大大增大B的浓度使其在反应过程中浓度变化很小或基本不变,则可把C B^β当做常数并入速率常数k中,得r=k’(C A^α),于是该反应就变为α级的反应,称此种反应为准α级反应。
反应级数可根据大量的实验数据通过积分法、微分法、半衰期法等方法确定,在化工生产中,不知其准确反应历程的情况下,可以通过这些方法确定反应的级数以及速率常数。