西安交通大学电机学课件
- 格式:doc
- 大小:2.81 MB
- 文档页数:176







三相变压器的电压比是指(A)之比。
A、一、二次侧相电动势B、一、二次侧线电动势C、一二次侧线电压D、一二次侧相电压一台并励直流电动机拖动一台它励直流发电机。
如果发电机的励磁电流和负载电阻均保持不变,而电动机的转速有所下降,发电机的输出功率将() 减小变压器负载呈容性,负载增加时,副边电压(C)。
A.呈上升趋势B.不变C.可能上升或下降两台变压器并联运行时,其负荷与短路阻抗(B)分配。
A.大小成反比B.标幺值成反比C.标幺值成正异步电动机定子漏磁通是由( A )A. 定子磁动势产生的B. 转子磁动势产生的C. 气隙磁动势产生的D. 定、转子磁动势共同产生的变压器负载电流不变时,功率因数越大,其效率(D )(A) 越大(B)越小(C) 不变(D)与铁损耗、铜损耗比值有关一台三相异步电动机,频率为50Hz,极对数为2,则同步转速为(B)r/min。
(A) 1000 (B) 1500 (C) 3000 (D) 750一台变比K=3的三相变压器,在低压侧加额定电压,测出空载功率P0=3000W,若在高压侧加额定电压,则功率为(3000瓦)异步电机转子电流频率随着转速升高将(C)。
A、变大B、变小C、不变D、先变大后变小直流电动机采用降低电源电压的方法起动,其目的是( B )A、使起动过程平稳;B、减小起动电流;C、减小起动转矩;D、节省电能一台三相感应电动机其额定值为0.75(功率因数),0.8(效率),3Kw,380V(Y)。
额定运行时定子电流为( D : 7.6A)A 6.5A B7.3A C6.08A D 7.6A一台变比为的变压器,从低压侧做空载试验,求得二次侧的励磁阻抗标幺值为16,则一次侧的励磁阻抗标幺值是( A )(A)16 (B)1600 (C) 0.16 (D)160升压变压器一次绕组的每匝电动势( A )二次绕组的每匝电动势。
(A) 等于(B) 大于(C) 小于(D) 不能确定异步电动机带恒转矩负载运行,电源电压下降,当电动机稳定运行后,此时电动机的电磁转矩( C )(A) 变小(B) 变大(C) 不变(D) 不确定对称三相交流绕组中通入对称的三相正弦交流电流,产生:( C )A、椭圆形B、脉振C、圆形D、方形空间按正弦分布的磁场波以n(r/min)转速切割一短距线圈感应的电动势与切割整距线圈时相比,感应电势将( C )。


第一篇直流电机
二、直流发电机原理(机械能--->直流电能)( Principles of DC Generator)
2-2 空载时直流电机的磁场
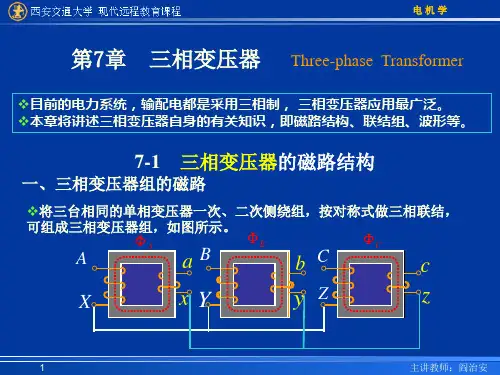
一、直流电机的磁通路径
磁路从主磁极1出发经气隙1-电枢齿1-电枢轭-电枢齿2-气隙2-主磁极2-定二、空载磁通密度波形
)。
为一条直线,考虑到转速略有
为一条略微上
下降很小,
K
仪用变压器。
(2)工作原理
1.当一次绕组接交流电压后,就有激磁电流i0存在,该电流在铁心中可产生一个交变的
主磁通Φ。
2.Ф在两个绕组中分别产生感应电势e1和e2
e1=-N1 dФ/dt e2=-N2 dФ/dt
3.若略去绕组电阻和漏抗压降,则以上两式之比为:
U1/U2≈(-e1)/(-e2)=N1/N2
4.U1/U2≈(-e1)/(-e2)=N1/N2=k,k定义为变压器的变比。
即:U1/U2=N1/N2 从此式可以看出,
若固定U1,只要改变匝数比即可达到改变电压的目的了,即:
若使 N2>N1,则为升压变压器(step-up transformer);
若使 N2<N1,则为降压变压器(step-down transformer)。
e1σ= -N1 dФ1σ/dt
二.电势公式及电势平衡方程式推导
∙空载时,主磁通Ф在一次侧产生感应电势E1,在二次侧产生感应电势E2,一次侧的漏磁通Ф1σ在一次侧漏抗电势E1σ。
∙假设磁通为正弦波Ф=Фm sin ωt 则
e1= -N1 dΦ/dt=-N1 dФm sin ωt/dt
= -N1Фmωcosωt=N1Фmωsin (ωt-90°)
=E1m sin (ωt-90°)
∙电势在相位上永远滞后于它所匝链的磁通90o。
∙其最大值:E1m= ω N1Фm = 2π f N1Фm
其有效值:E1=E1m/sqrt(2)
= 2π f N1Фm/1.414
= 4.44 f N1Φm
∙这就是电机学最重要的“4.44”公式。
说明了感应电势E1与磁通Φm、频率f、绕组匝数N1成正比。
∙同样可以推出e2和e1σ的公式:
e2=E2m sin(ωt-90°)
E2m=N2Φmω
E2=4.44 f N2 Φm
e1σ=-N1dΦ1σ/dt
=N1Φ1σmωsin(ωt-90°)
E1σm=ω N1Φ1σm
E1σ=4.44 f N1Φ1σm
∙由于漏磁路的磁导率μo为常数,Φ1σm =L1σI I0,故E1σ=4.44f N12L1σI0=X1σI0,即E1σ可用漏抗压降的形式表示。
∙以上推导涉及到的电磁量均为正弦变化,可以用相量来表示。
用相量时可同时表示有效值和相位。
E1σ=-jX1σI0
∙考虑到一次侧绕组的电阻压降后,其电势平衡方程为 U1=-E1-E1σ+R1I0=-E1+jX1σI0+R1I0 =-E1+I0Z1
∙二次侧无电流,故:E2=U2
∙对于一次侧来说,电阻压降和漏抗压降都很小。
所以U1≈-E1=4.44 f N1Φm,可见变压器的磁通主要由电源电压U1、频率f 和一次侧绕组的匝数N1决定。
在设计时,若电压U1和频率f给定,则变压器磁通由匝数N1决定。
对于制成运行的变压器,其磁通Φ可以由电压U1和频率f控制。
∙问题6-2:220V、50Hz的变压器空载接到220V、25Hz的电源上,后果如何?
∙问题6-3:220V、50Hz的变压器空载接到220直流电源上,后果如何?
三.变压器的变比k 和电压比K
a) 变比k:指变压器1、2次绕组的电势之比。
1.k=E1/E2=(4.44fN1Φm)/(4.44fN2Φm)=N1/N2
2.变比k等于匝数比。
二次侧N2\U2\I2\E2\R2\X2σ\R L\X L 为实际值
折算后
二次侧N2'\U2'\I2'\E2'\R2'\X2σ'\R L'\ X L' 为折算值(1)电势、电压折算
E2'=4.44 f N1Фm=E1
E2=4.44 f N2Фm
∙所以E2'/E2=N1/N2=k,E2'=kE2
∙同样U2'=kU2 (2)电流折算 N1I2'=N2I2 I2'=I2N2/N1=I2/k
(3)阻抗折算
∙阻抗折算要保持功率/损耗不变 (I2')2R2'=(I2)2R2
R2'=(I2/I2')2 R2=k2R2
(I2')2X2σ'=(I2)2X2σ
X2σ' = (I2/I2')2 X2σ= k2X2σ
(I2')2 R L'=(I2)2 R L
R L'=(I2/I2')2 R L= k2 R L
(I2')2X L'=(I2)2X L
X L'=(I2/I2’)2 X L= k2X L
(1) 折算后的方程 U1= -E1+I1(R1+jX1σ)
U2'= E2' - I2'(R2+jX2σ)
I1+I2'=I m≈I0
- E1= - E2'= I m (R m+jX m) = I m Z m
(2) T型等效电路
∙如果知道效电路中各个参数、负载阻抗和电源电压,则可计算出各支路电流I1、I2'、I m/输出电压U2'/损耗/效率等,通过反折算就能计算出二次侧实际电流I2=kI2'和实际电压
U2=U2'/k。
(2)简化等效电路
∙由于励磁阻抗很大,I m很小,有时就将励磁支路舍掉,得到所谓简化等效电路。
∙简化等效电路中,Z k=R k+jX k,R k与X k构成变压器的漏阻抗,也叫短路阻抗,即变压器的副边短路时呈现的阻抗。
R k为短路电阻,X k为短路电抗。
Z L'为折算到一次侧的负载阻抗。
R k=R1+R2' X k=X1σ+X2σ'Z k=R k+jX k
∙用简化等效电路计算的结果也能够满足工程精度要求。
∙当需要在二次侧基础上分析问题时,可将一次侧折算到二次侧。
当用欧姆数说明阻抗大小时,必须指明是从哪边看进去的阻抗。
∙从一次侧看进去的阻抗是从二次侧看进去的阻抗的k2倍。
四.变压器负载运行时的相量图
根据方程式(equation)或者等效电路,可以画出相
量图,从而了解变压器中电压、电流、磁通等量之
间的相位和大小关系。
等效电路,方程式和相量图是用来研究分析变压器
的三种基本手段,是对一个问题的三种表述,相量
图对各物理量的相位更直观显现出来。
定性分析时,
用相量图较为清楚;定量计算时,则用等效电路。
6-4 变压器的参数测定和标幺值
∙等效电路中的各种R1、R2、X1σ、X2σ、R m、X m、
k 等,对变压器运行性能有重大影响。
∙这些参数通常通过空载试验和稳态短路试
验来求得。